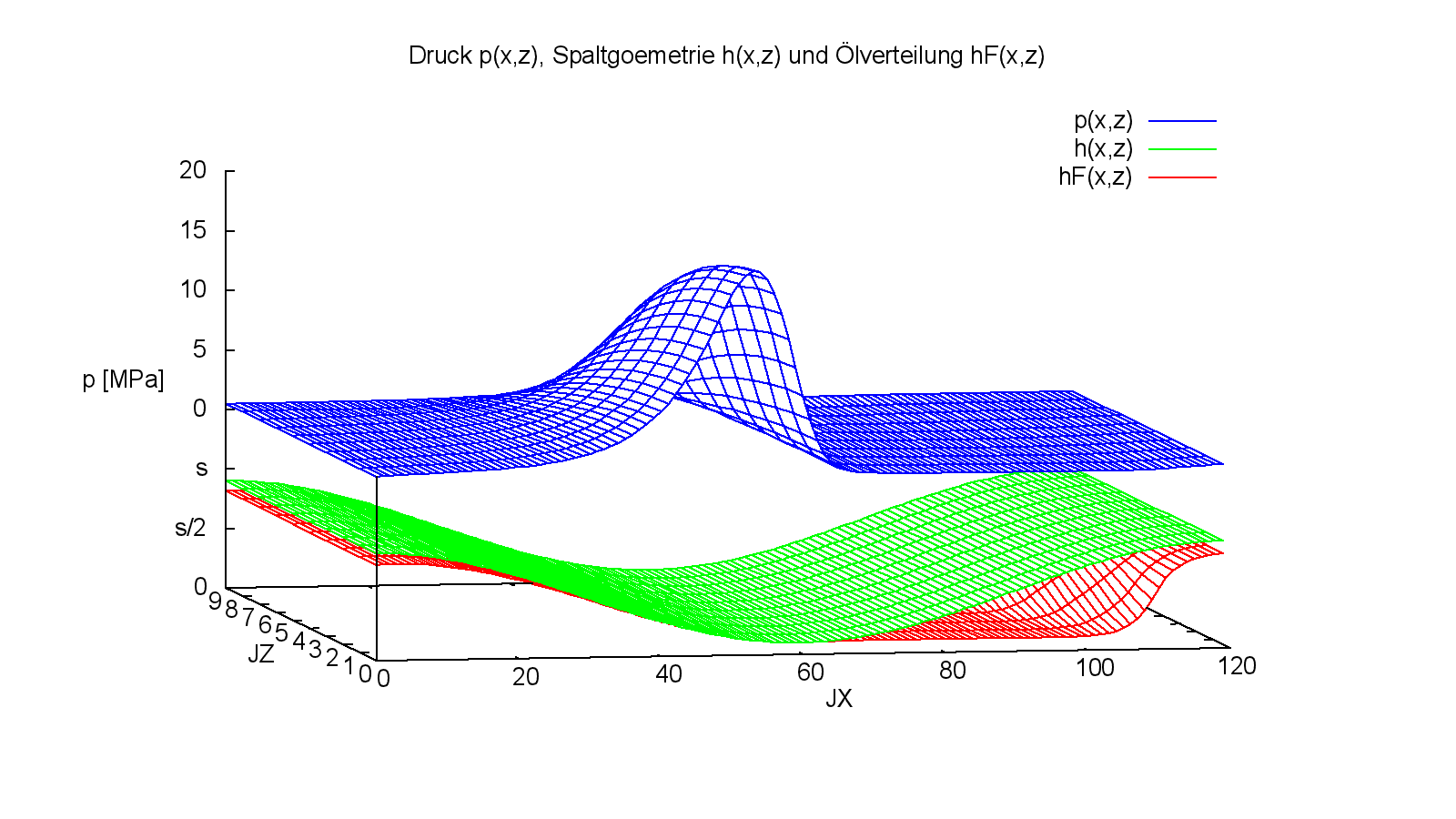
Bild 4.061: Druckverteilung p, Spaltgeometrie h und Schmierflüssigkeitsverteilung hF im stationären Zustand des Demonstrationsbeispiels Demo01 (Bilddatei: Demo01-Dim-3d-Abw-p-h-hF-JT=21.png)
In diesem Abschnitt soll an ausgewählten Demonstrationsbeispielen die Arbeit mit dem Programm illustriert werden. Ergebnisse werden dargestellt und diskutiert. Es wird auf mögliche Probleme hingewiesen und es werden Tipps zu ihrer Beseitigung gegeben. Zu allen gezeigten Demonstrationsbeispielen sind die primären Eingabe- und Ergebnisdatensätze in Textdateien "Demo...txt" dokumentiert und im Verzeichnis "DatenDemo" abgelegt. Dieses Verzeichnis kann unabhängig vom Programm und von der Dokumentation aus dem Internet heruntergeladen werden (siehe Abschnitt 4.2.2). Die in der Dokumentation gezeigten Bilder und Animationen sind in png-Bilddateien und wmv-Videodateien in den Verzeichnissen der Dokumentation "sirius-doku2-0/bilder" und "sirius-doku2-0/animationen" abgelegt. So können die Ergebnisse mit eigenen Berechnungen nachvollzogen werden.
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo01.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Das Demonstrationsbeispiel Demo01 ist identisch mit den Anfangsdaten beim Start des Programms. Mit dem Start des Programms werden alle potentiellen Eingabedaten automatisch mit Anfangsdaten belegt. Diese sind so gewählt, dass sie bereits einen vollständigen Eingabedatensatz eines einfachen Lagerbeispiels darstellen und ohne weitere Datenbearbeitung dieses Bespiel berechnet werden kann. Siehe dazu auch Abschnitt 1.4 "Schnelleinstieg".
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale dieses Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2) -2- Verlagerung der Welle vorgegeben (Last = 1) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale ideal zylindrisch und starr (Schale = 1) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Nach dem Start des Programms brauchst Du Dich nur bis zum Solver durchklicken und dort mit der Auswahl der Aktion -1- die komplette Berechnung zu starten. Das Ergebnis liegt nach wenigen Sekunden vor.
Routine: Druckverlauf2
Berechnung des Druckverlaufs P(Z,X,T) ueber 20 Zeitschritte
JT= 2
JT= 3
JT= 4
JT= 5
JT= 6
JT= 7
JT= 8
JT= 9
JT= 10
JT= 11
JT= 12
JT= 13
JT= 14
JT= 15
JT= 16
JT= 17
JT= 18
JT= 19
JT= 20
JT= 21
----------------------------------------------------------------------
Aktuelle zeitvariable Eingabe- und Ergebnisdaten
JT hMin t e xe f xf pMax
mm s mm grd kN grd MPa
1 0.0100 0.0000 0.0400 0.0000 0.0000 -12.4645 0.5236
2 0.0100 0.0240 0.0400 0.0000 19.5134 -38.2971 14.5279
3 0.0100 0.0480 0.0400 0.0000 23.4112 -36.0907 17.0436
4 0.0100 0.0720 0.0400 0.0000 23.7119 -35.8862 17.1421
5 0.0100 0.0960 0.0400 0.0000 23.9271 -35.5217 17.1789
6 0.0100 0.1200 0.0400 0.0000 23.9873 -35.4372 17.1881
7 0.0100 0.1440 0.0400 0.0000 24.0698 -35.2499 17.1962
8 0.0100 0.1680 0.0400 0.0000 24.1954 -34.5165 17.1983
9 0.0100 0.1920 0.0400 0.0000 24.0652 -35.1725 17.1962
10 0.0100 0.2160 0.0400 0.0000 24.0940 -35.1256 17.1976
11 0.0100 0.2400 0.0400 0.0000 24.1054 -35.1037 17.1982
12 0.0100 0.2640 0.0400 0.0000 24.1131 -35.0871 17.1987
13 0.0100 0.2880 0.0400 0.0000 24.1151 -35.0833 17.1988
14 0.0100 0.3120 0.0400 0.0000 24.1159 -35.0816 17.1988
15 0.0100 0.3360 0.0400 0.0000 24.1163 -35.0805 17.1988
16 0.0100 0.3600 0.0400 0.0000 24.1162 -35.0800 17.1988
17 0.0100 0.3840 0.0400 0.0000 24.1161 -35.0799 17.1987
18 0.0100 0.4080 0.0400 0.0000 24.1159 -35.0802 17.1987
19 0.0100 0.4320 0.0400 0.0000 24.1158 -35.0805 17.1987
20 0.0100 0.4560 0.0400 0.0000 24.1159 -35.0807 17.1987
21 0.0100 0.4800 0.0400 0.0000 24.1159 -35.0808 17.1987
mm s mm grd kN grd MPa
JT hMin t e xe f xf pMax
Aktuelle zeitvariable Eingabe- und Ergebnisdaten
Das Programm hat nun über eine Anlaufrechnung von 20 Zeitschritten bzw. 4 Wellenumdrehungen den stationären Zustand eines statisch belasteten Lagers berechnet.

Bild 4.061: Druckverteilung p, Spaltgeometrie h und Schmierflüssigkeitsverteilung hF im stationären Zustand des Demonstrationsbeispiels Demo01 (Bilddatei: Demo01-Dim-3d-Abw-p-h-hF-JT=21.png)
Bild 4.061 zeigt für den letzten berechneten Zeitpunkt, der den stationären Zustand des statisch belasteten Lagers darstellt, die Druckverteilung p, die Spaltgeometrie h und die Schmierflüssigkeitsverteilung hF.
Erläuterungen, Hinweise, Tipps:
Im aktuellen Beispiel wird mit der erweiterten Reynoldsschen Differentialgleichung gerechnet (Theo=2), bei der auch Kavitation berücksichtigt wird und die Schmiermittelverteilung im Schmierspalt berechnet wird. Deshalb ist hier trotz der stationären Wellenverlagerung eine Anlaufrechnung über mehrere Zeitschritte erforderlich, bis sich der stationäre Zustand eingestellt hat.
Wenn nur das stationäre Endergebnis dokumentiert werden soll und der Ablauf der Anlaufrechnung nicht interessiert, kannst Du nach dieser Berechnung folgendermaßen weiter verfahren:
Gehe zurück in den PreProzessor.
Gehe in das Hauptmenü:
---------------------------------------------------------------------- Eingeben bzw. aendern der konstanten Parameter ---------------------------------------------------------------------- ... -12- NT = 21 - -Anzahl der zu berechnenden Zeitpunkte ... -d- U m s c h a l t e n auf dimensionslose Eingabe (Dim=2 -> Dim=3) -a- Zurueck zum Anfang der Eingabe -z- Zurueck zum vorhergehenden Hauptmenuund ändere die Anzahl der zu berechnenden Zeitschritte auf NT=2 und ändere evtl. auch den Endzeitpunkt tEnd.W e i t e r zum naechsten Hauptmenu Eingabe: 12 Ist-Wert: NT = 21 -Anzahl der zu berechnenden Zeitpunkte Bedingung: 1 < NT <= 620 Neuen Wert eingeben: 2
Gehe weiter in das Hauptmenü:
----------------------------------------------------------------------
Festlegen der Anfangsdruckverteilung
----------------------------------------------------------------------
-1- Anfangsdruckverteilung auf Standardanfangsdruck zuruecksetzen
-2- Druckwerte P(X,Z), PPu, PTa und Stromwerte QPu, QVe des Zeit-
punktes JT zu den neuen Anfangswerten machen
-4- Anfangsdruckverteilung aus einer Datei lesen
-d- U m s c h a l t e n auf dimensionslose Eingabe (Dim=2 -> Dim=3)
-a- Zurueck zum Anfang der Eingabe
-z- Zurueck zum vorhergehenden Hauptmenu
W e i t e r zum naechsten Hauptmenu
Eingabe:
2
Druck- und Stromdaten vom Zeitpunkt JT zu den neuen Anfangsdaten machen
-...- Zeitpunkt JT, 2 <= JT <= 21
< 21 > Waehle den letzten berechneten Zeitpunkt NT2 = 21
- z - Z u r u e c k zum Hauptmenu
Eingabe:
Wähle die Aktion -2- und in der folgenden Abfrage den letzten Zeitpunkt <21>.
Gehe weiter in den Solver und starte mit Aktion -1- erneut die Berechnung. Jetzt wird nur noch ein Zeitpunkt JT=2 berechnet.
====================================================================== SOLVER: Berechnung ausfuehren ====================================================================== HINWEIS: Ueber das Zeitintervall JT= 1 bis 21 wurde bereits eine Berechnung ausgefuehrt. Es ist keine weitere Berechnung erforderlich. -1- Komplette Berechnung von JT= 1 bis 2 ausfuehren -2- Berechnung ueber ein Zeitintervall JT= NT1 bis NT3 ausfuehren -a- Zurueck zum PreProzessor (Eingabedaten bearbeiten)Weiter zum PostProzessor (Ergebnisse auswerten und sichern) Eingabe: 1 Routine: Druckverlauf2 Berechnung des Druckverlaufs P(Z,X,T) ueber 1 Zeitschritte JT= 2 ---------------------------------------------------------------------- Aktuelle zeitvariable Eingabe- und Ergebnisdaten JT hMin t e xe f xf pMax mm s mm grd kN grd MPa 1 0.0100 0.0000 0.0400 0.0000 24.1159 -35.0808 17.1987 2 0.0100 0.4800 0.0400 0.0000 24.1184 -35.0797 17.1988 mm s mm grd kN grd MPa JT hMin t e xe f xf pMax Aktuelle zeitvariable Eingabe- und Ergebnisdaten
Da zum Zeitpunkt JT=1 bereits die stationäre Lösung vorlag, müssen die Ergebnisse zum Zeitpunkt JT=2 mit denen vom Zeitpunkt 1 übereinstimmen. Wenn jetzt dieses Ergebnis abgespeichert wird, werden nur die Druckverteilungen der 2 Zeitpunkte gespeichert und die erfolgte Anlaufrechnung wird nicht mit dokumentiert. Damit wird Speicherplatz gespart. Dabei ist mit den 2 Zeitpunkten auch dokumentiert, ob auch tatsächlich der stationäre Zustand erreicht ist. Das Ergebnis dieser 2.Berechnung ist in der Datei "Demo01-1.txt" abgelegt.
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo02.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:

Als nächstes Demonstrationsbeispiel soll das gleiche einfache Lager des Demonstrationsbeispiels "Demo01" berechnet werden, dieses Mal aber mit der klassischen Reynoldsschen Differentialgleichung mit "Gümbelschen Randbedingungen".
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Reynoldssche Dgl. mit "Guembelscher Randbedingung" (Theo = 1) -2- Verlagerung der Welle vorgegeben (Last = 1) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale ideal zylindrisch und starr (Schale = 1) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Nur bei der Lagervariante eines stationär belasteten Lagers mit vorgegebener Wellenverlagerung, berechnet mit der klassischen Reynoldsschen DGL, ist keine Anlaufrechnung erforderlich. Das Programm legt trotzdem für den 1.Zeitpunkt JT=1 Anfangsbedingungen fest, obwohl diese eigentlich nicht benötigt werden. Mit dem Zeitpunkt NT=2 wird aber bereits das endgültige stationäre Ergebnis geliefert.
Bild 4.063 zeigt für den 2.Zeitpunkt, der den stationären Zustand des statisch belasteten Lagers darstellt, die Druckverteilung p und die Spaltgeometrie h. Eine Schmiermittelverteilung im Schmierspalt kann hier nicht gezeigt werden, weil nach der klassischen Reynoldsschen DGL der Schmierspalt als vollständig mit Flüssigkeit gefüllt angenommen wird, der örtliche Füllungsgrad deshalb im gesamten Schmierspalt F=1 ist und h·F=h. Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo03.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
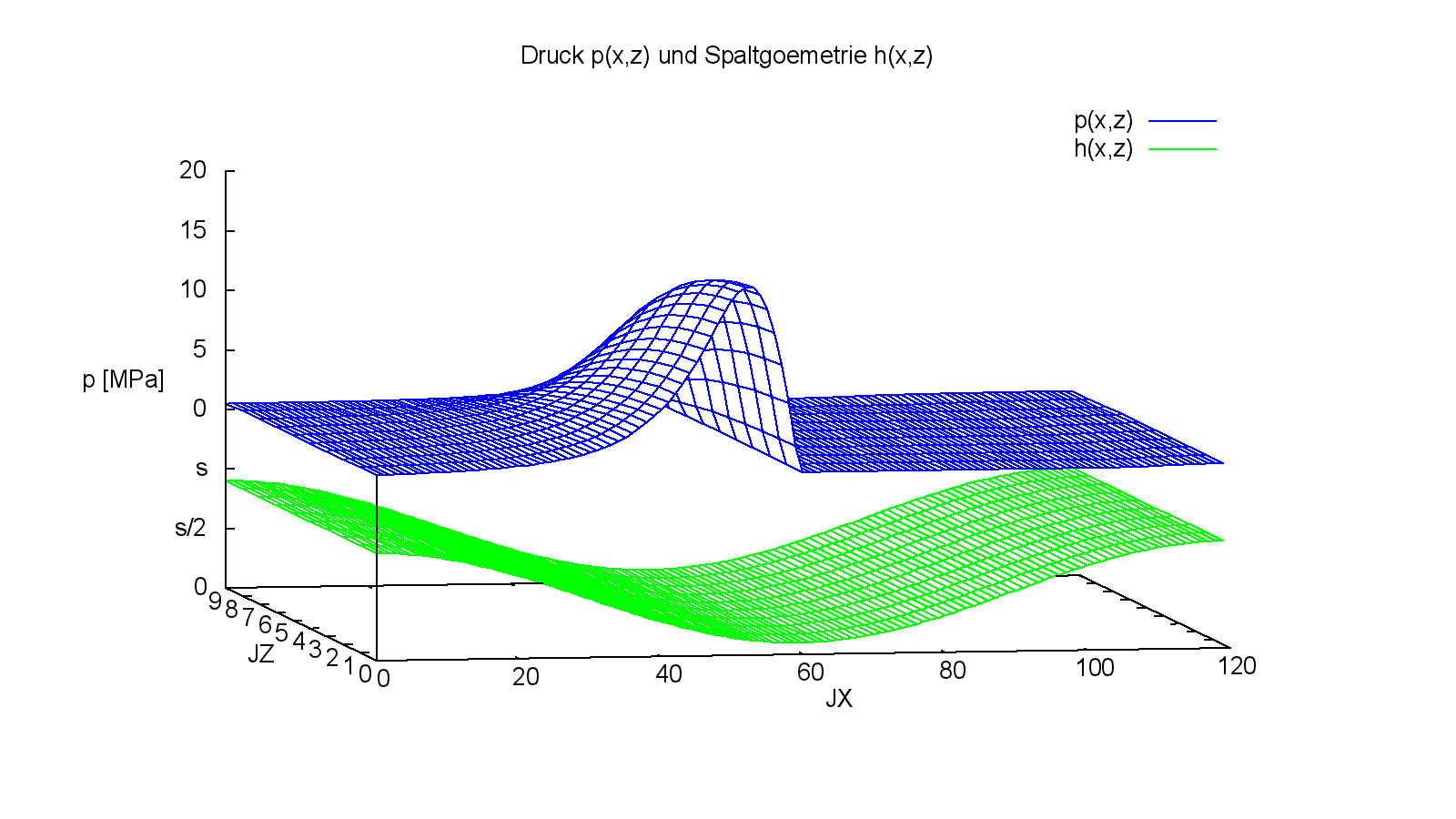
Bild 4.063: Druckverteilung p und Spaltgeometrie h im stationären Zustand des Demonstrationsbeispiels Demo02 (Bilddatei: Demo02-Dim-3d-Abw-p-h-JT=2.png)
4.8.3 Demo03: Berechnung der Verlagerungsbahn aus einer vorgegebenen Lagerbelastung
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2) -2- Belastung des Lagers vorgegeben (Last = 2) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale ideal zylindrisch und starr (Schale = 1) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Auszer den Bezugsparametern alle anderen dimensionslos (Dim = 3)
Die Berechnung einer Wellenverlagerung aus einer vorgegebenen Lagerbelastung ist in der Praxis der Auslegung eines Gleitlagers der relevante Fall. Hier ist im stationären Fall eine Anlaufrechnung nicht nur wegen der Anwendung der erweiterten Reynoldsschen DGL erfotderlich, sondern auch deshalb, weil die Wellenverlagerung, beginnend von einem angenommenen Anfangszustand, iterativ ermittelt werden muss, bis die Lagerbelastung und das Integral des Schmierfilmdrucks ein Gleichgewicht bilden.
Zur Abwechslung wird bei diesem Beispiel an der Bedienoberfläche mit dimensionslosen Daten gearbeitet (Dim=3).
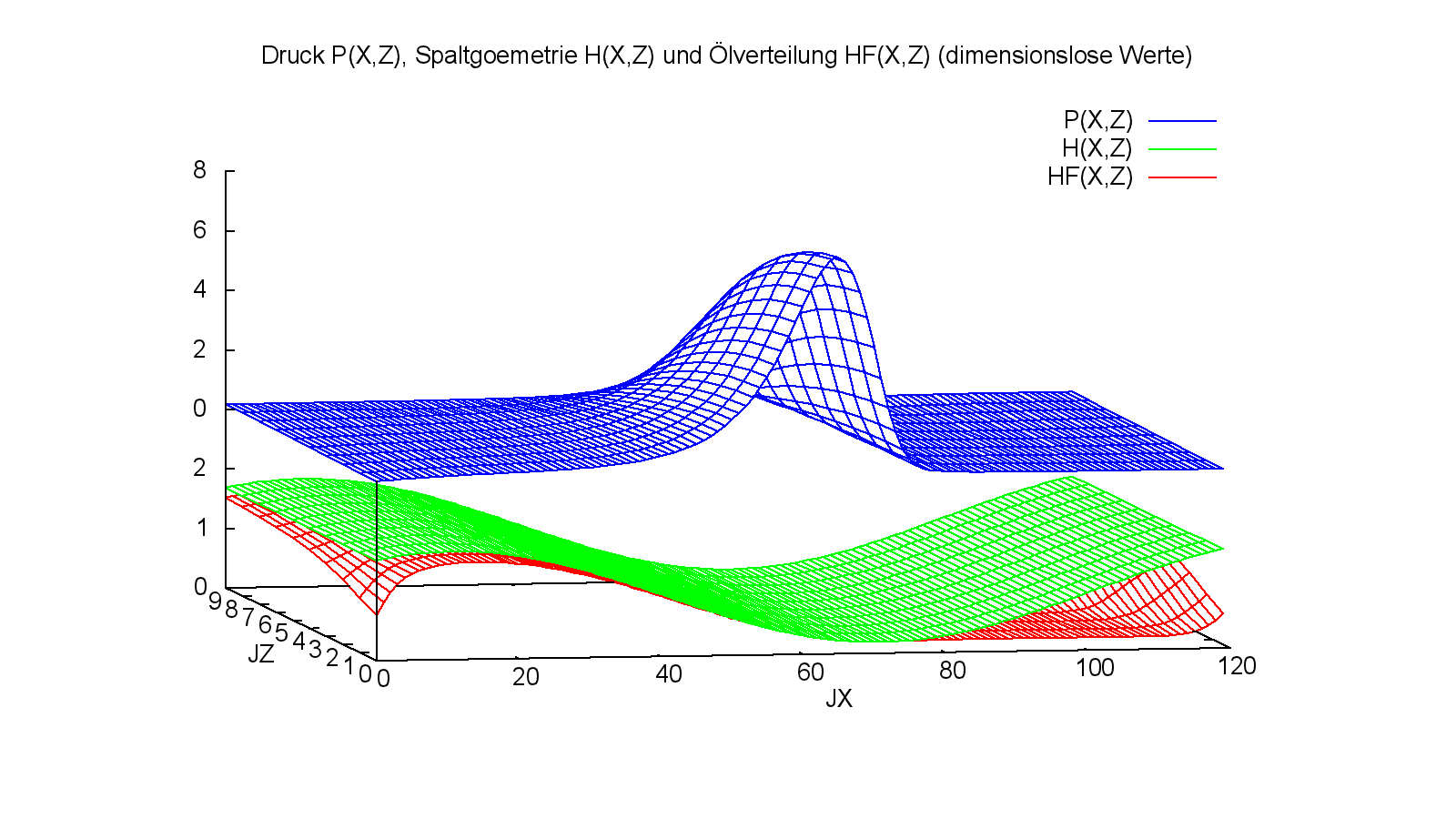
Bild 4.065 zeigt für den letzten berechneten Zeitpunkt, der den stationären Zustand des statisch belasteten Lagers darstellt, die dimensionslose Druckverteilung P, Spaltgeometrie H und Schmierflüssigkeitsverteilung HF. Die zugehörige Animation zeigt den Anlaufprozess.
Bild 4.066 zeigt für die erfolgte Anlaufrechnung die Verlagerungsbahn des Wellenmittelpunktes im dimensionslosen Spielraum, von einer angenommenen konzentrischen Anfangslage bis zum stationären Endpunkt.
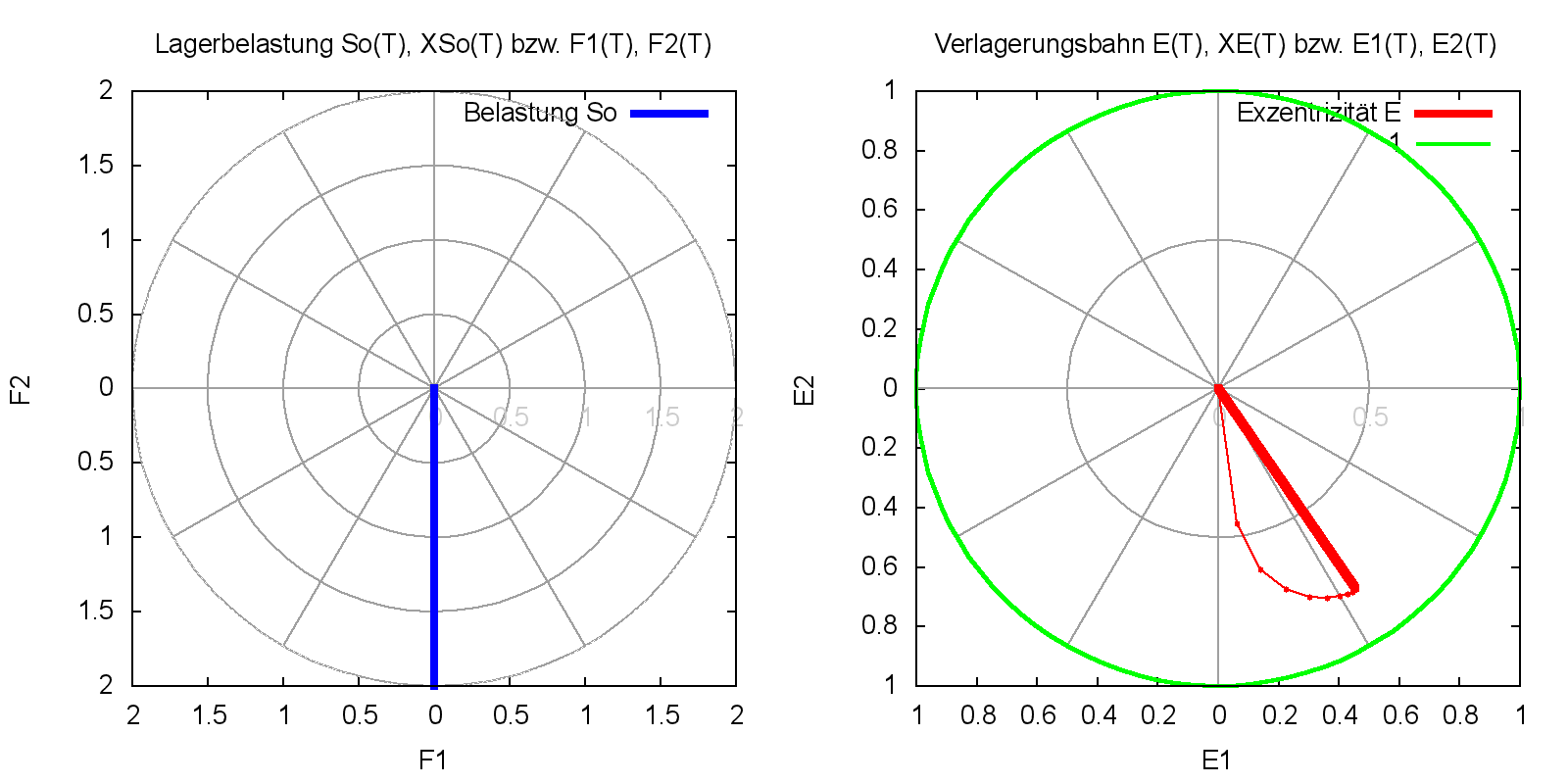
Bild 4.066: Wellenverlagerungsbahn des Anlaufprozesses für das Demonstrationsbeispiel Demo03 (Bilddatei: Demo03-2d-Pol-So-E-Punkte-JT=21.png)
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo04.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2) -2- Belastung des Lagers vorgegeben (Last = 2) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale ideal zylindrisch und starr (Schale = 1) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Die Angaben des folgenden Hauptmenüs beschreiben das periphere Schmiermittelversorgungssystem sowohl qualitativ als auch quantitativ.
----------------------------------------------------------------------
Universal-Schmiermittel-Versorgungssystem
----------------------------------------------------------------------
NPu = 1 Anzahl der Schmiermittelpumpe
NTa = 1 Anzahl der Schmiertaschen
NVe = 1 Anzahl der Verbindungsleitungen
NVar= 1 Anzahl der Geraetevarianten
P u m p e n :
max.Pumpendruck max. Oelstrom
JPu pPuMax(JPu) qPuMax(JPu)
1 0.3000 MPa 0.5000 L/min
G e r a e t e v a r i a n t e n in den Verbindungsleitungen:
1 Nur Kapillare bzw. Leitungswiderstand
1 1 ccp = 1.0000 mm^-3 Widerstandsbeiwert
V e r b i n d u n g s l e i t u n g e n :
JVe Nummer der Verbindungsleitung
JPu Nummer der verbundenen Pumpe
JVar Nummer der Geraetevariante in der Leitung
JTa Nummer der verbundenen Schmiertasche
Typ Nummer des Geraetetyps
JVe JPu JVar JTa Typ Bezeichnung des Geraetetyps
1 1 >-- 1--< 1 1 Nur Kapillare bzw. Leitungswiderstand
Die Beschreibung der Erzeugung einer Schmiertasche ist im Abschnitt 4.4.8.3 erläutert. Die Eingaben zum peripheren Schmiermittelversorgungssystem sind im Abschnitt 4.4.9 beschrieben.
Bei diesem Demonstrationsbeispiel wurde mit einer Gitterteilung von NX=360 gearbeitet, wie sie bei praxisnahen Berechnungen mit Schmiertaschen üblich ist, um genaue Ergebnisse zu erhalten und mögliche Instabilitäten der Iteration weitgehend zu vermeiden. Um bei den 3d-Bildern den Funktionsverlauf besser erkennen zu können, wurde bei diesen Bildern nur jede 3.Gitterlinie gezeigt, so dass der Eindruck entstehen kann, dass mit nur NX=120 gearbeitet wurde. (Die Nummerierung des dargestellten Gitternetzes lässt sich in Gnuplot leider nicht verändern.)
Nachfolgende Bilder zeigen einige Darstellungsmöglichkeiten der Ergebnisse.
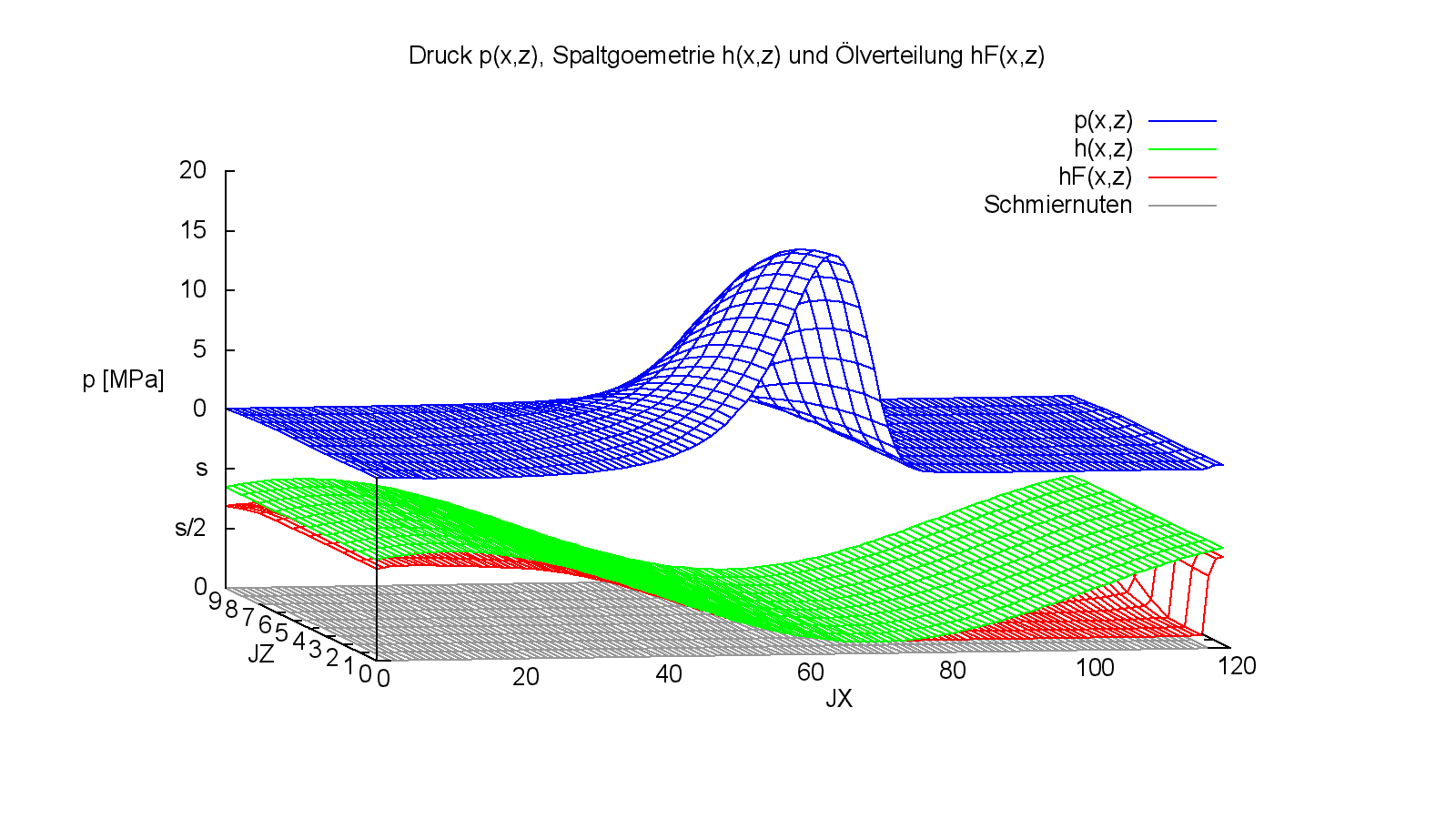
Bild 4.068: Druckverteilung p, Spaltgeometrie h und Schmierflüssigkeitsverteilung hF im stationären Zustand des Demonstrationsbeispiels Demo04 (Bilddatei: Demo04-Dim-3d-Abw-p-h-hF-Nut-JT=41.png)
Die Animation, auf die in der Bildunterschrift 4.069 verwiesen wird und auf die in der elektronischen Version der Dokumentation zugegriffen werden kann, zeigt den Verlauf der Anlaufrechnung.
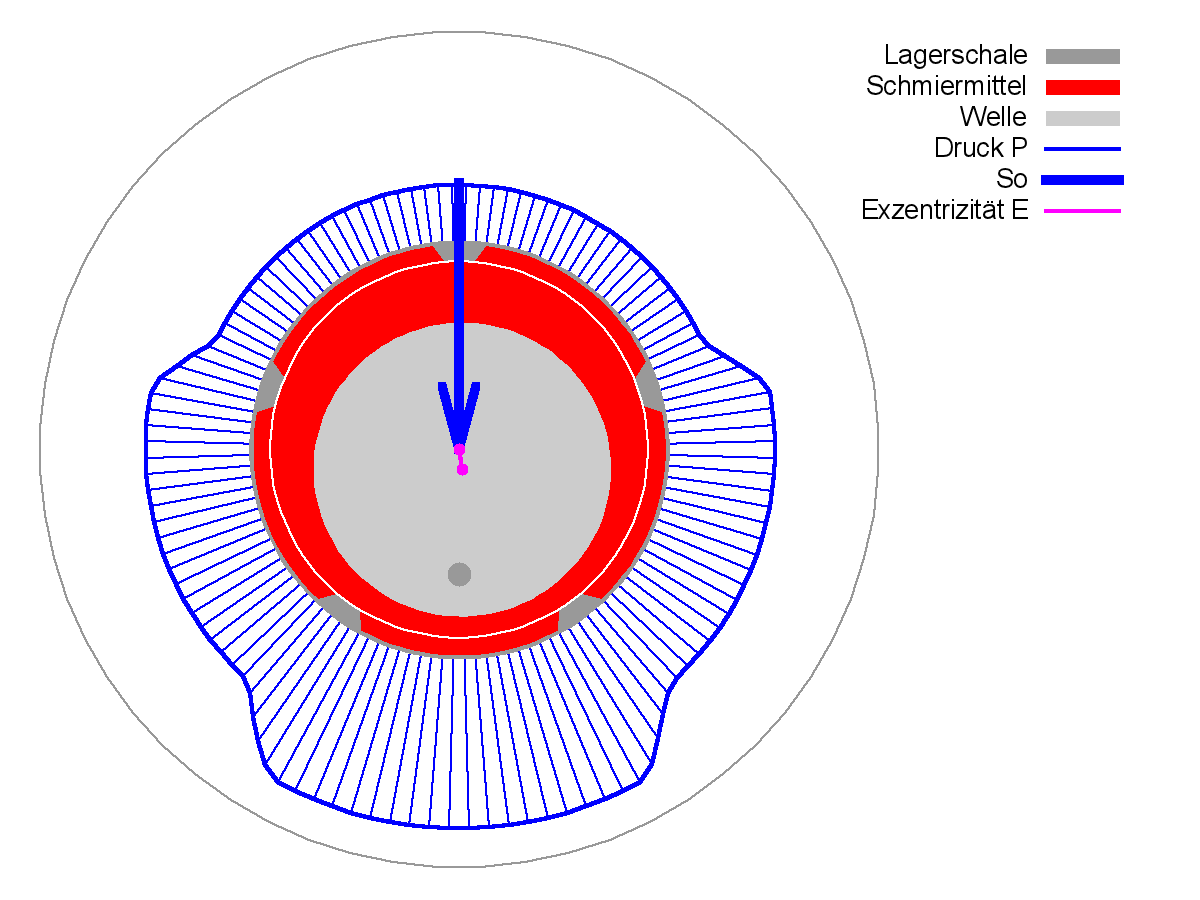
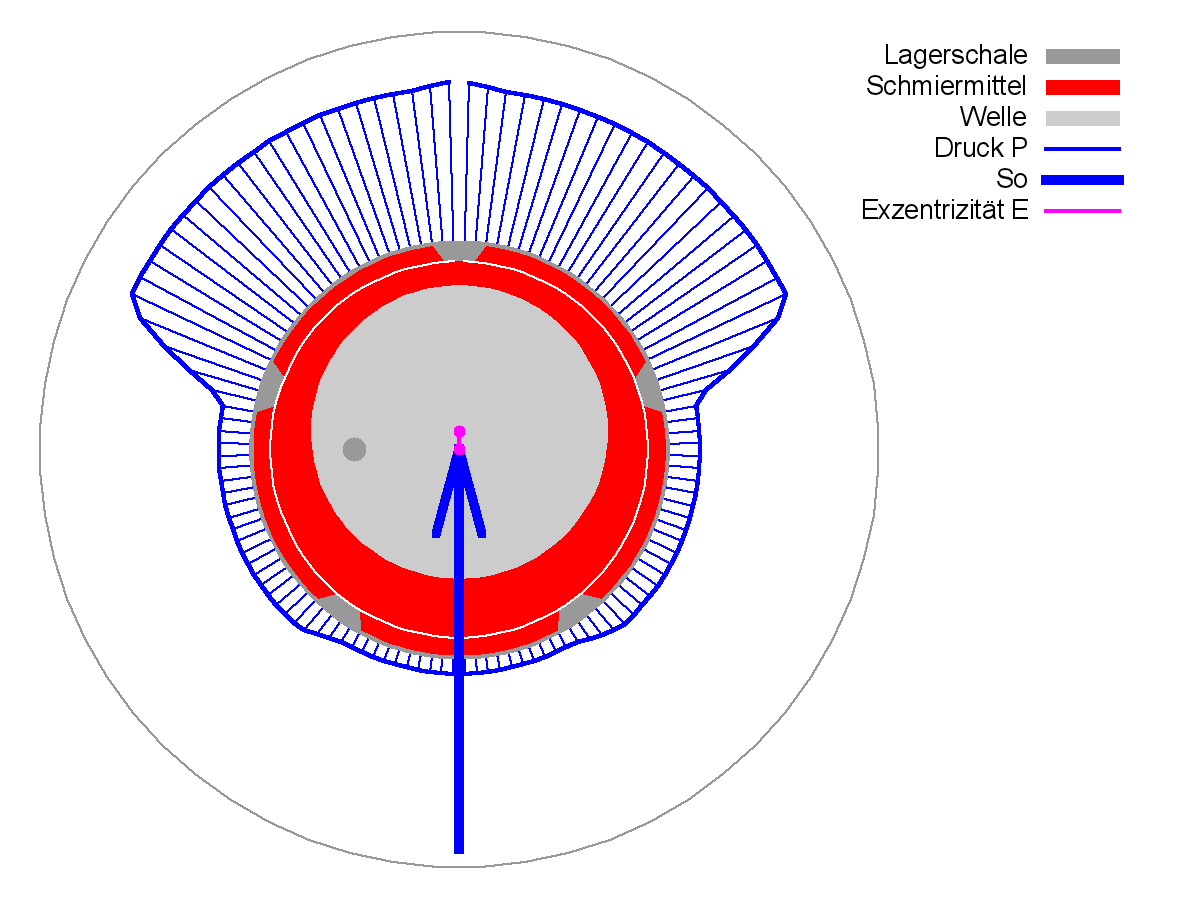
Bild 4.070 zeigt im rechten Diagramm die Verlagerungsbahn (rot) des Wellenmittelpunktes innerhalb des Spielraums (grün) der Anlaufrechnung bis zum stationären Zustand. Die dicke rote Linie gibt den Betrag und die Richtung der Wellenverlagerung im stationären Endzustand an (JT=41). Das linke Diagramm zeigt den Betrag und die Richtung der zeitlich konstanten Lagerbelastung (blau). Die konzentrische Lage des Wellenmittelpunktes als Anfangslage ist in vielen Fällen geeignet. Die Wahl des Anfangspunktes ist aber weitgehend frei. Besonders zweckmäßig ist es, wenn bereits eine Berechnung für einen ähnlichen Lastfall vorliegt und diese Ergebnisse als Anfangswerte für die neue Berechnung genutzt werden.
Wenn die Anlaufrechnung nicht von Interesse ist und nur das stationäre Endergebnis dokumentiert werden soll, ist, wie beim Demonstrationsbeispiel Demo01 (Abschnitt 4.8.1) beschrieben, zu verfahren. Für das Demonstrationsbeispiel Demo04 ist die verkürzte Dokumentation des stationären Endergebnisses in der Datei Demo04-1.txt abgelegt. Damit reduziert sich der erforderliche Speicherplatz von 1,8 MB auf 108 KB. Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo05.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
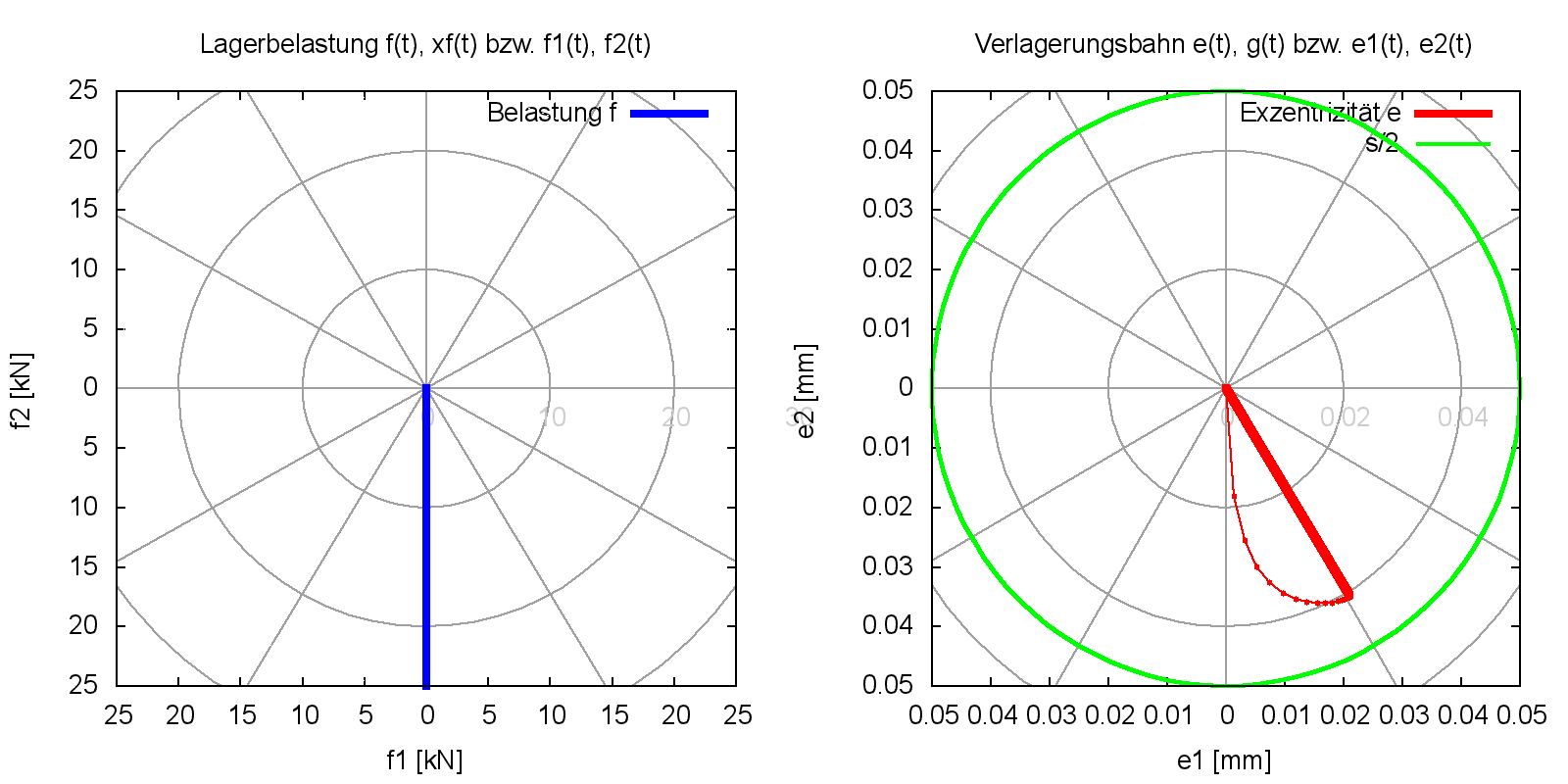
Bild 4.070: Verlagerungsbahn (rechts) während der Anlaufrechnung über 40 Zeitschritte bzw. 2 Wellenumdrehungen bis zum stationären Betriebszustand (Bilddatei: Demo04-Dim-2d-Pol-f-e-Punkte-JT=41.png)
4.8.5 Demo05: Wechselnd belastetes hydrodynamisches Lager
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
----------------------------------------------------------------------
Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp
----------------------------------------------------------------------
-1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2)
-2- Belastung des Lagers vorgegeben (Last = 2)
-3- Vollstaendig umschlossenes Lager (Vollum = 1)
-4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1)
-5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1)
-6- Gerade Welle (Biege = 1)
-7- Keine versetzten Lagerabschnitte (Versatz = 1)
-8- Welle ideal zylindrisch (Welle = 1)
-9- Lagerschale ideal zylindrisch und starr (Schale = 1)
-20- Evtl. einige Eingabeparameter zeitabhaengig (Dynamic = 2)
-21- Zeitschritte DT konstant (SchrittVar = 1)
-22- Omega konstant (OmegaVar = 1)
-24- F1(T)=F1Amp*sin(Omega1*T-Phi1)+F1Mit (LastVar = 5)
F2(T)=F2Amp*sin(Omega2*T-Phi2)+F2Mit
-30- Auszer den Bezugsparametern alle anderen dimensionslos (Dim = 3)
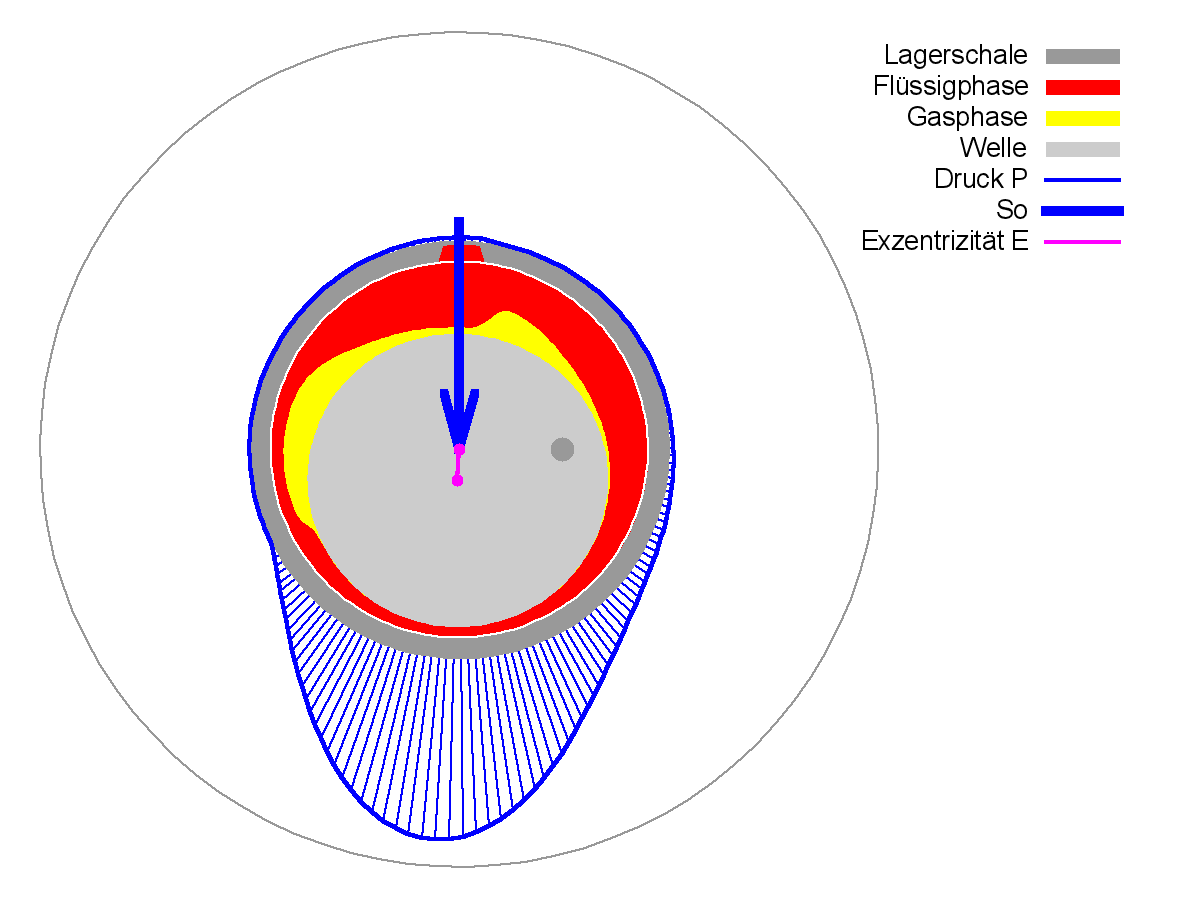
Das Demonstrationsbeispiel "Demo05" ist weitgehend identisch mit dem Demonstrationsbeispiel "Demo04". Der einzige Unterschied besteht darin, dass jetzt ein wechselnder Belastungsverlauf vorgegeben ist. Es werden 2 Wellenumdrehungen berechnet. Die 1.Umdrehung ist die Anlaufrechnung. Mit der zweiten Umdrehung ergibt die Berechnung bereits bei einem geschlossenen Lastzyklus auch einen geschlossenen Zyklus der Welleverlagerungsbahn, was Bild 4.072 zeigt.
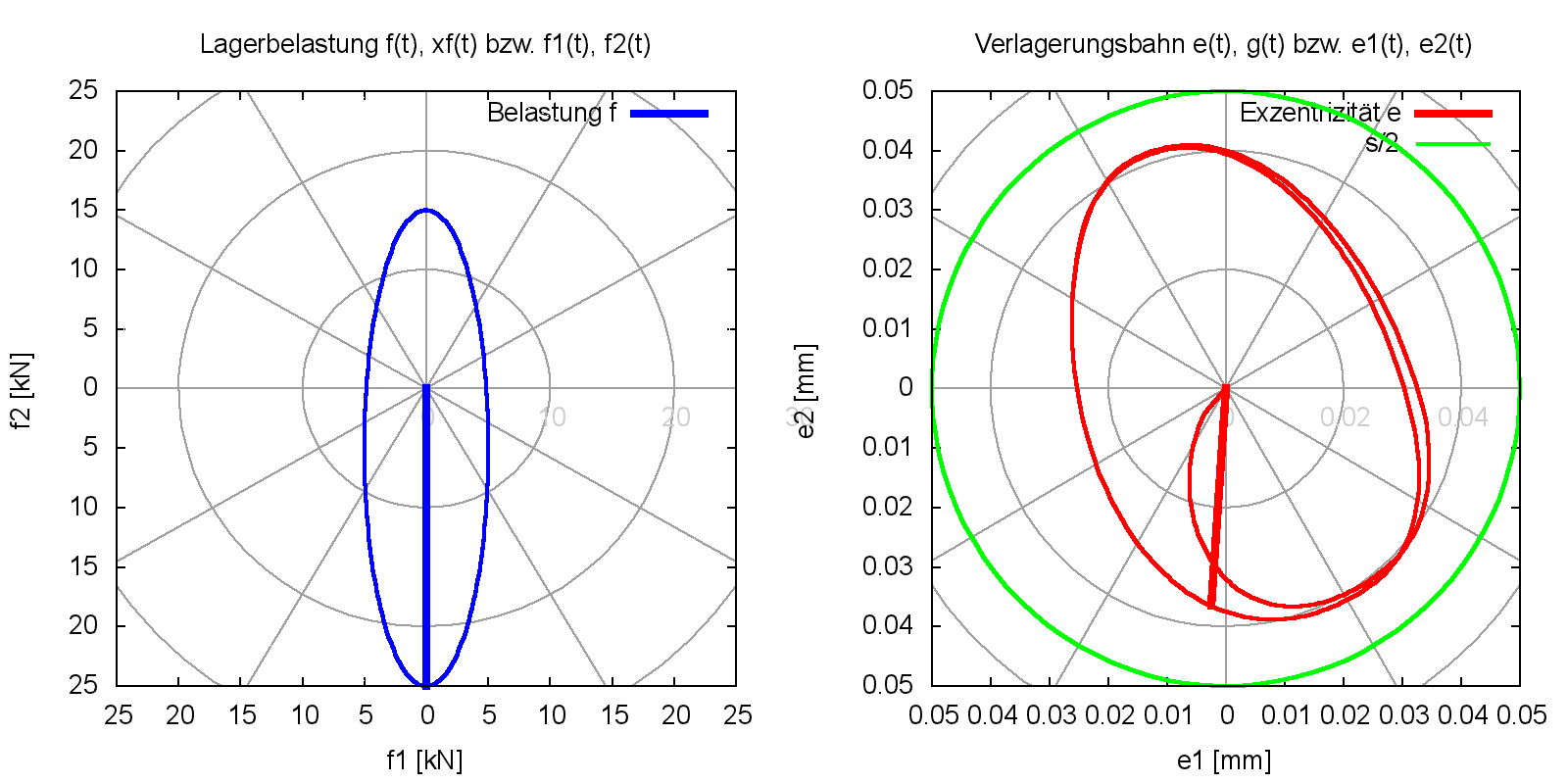
Während das statische Bild 4.072 den Verlauf der Verlagerungsbahn für beide Wellendrehungen zeigt, also auch die Anlaufrechnung, wird in der zugehörigen Animation nur die 2.Wellenumdrehung dargestellt und es ist gut zu erkennen, dass die berechnete Verlagerungsbahn bereits einen geschlossenen Zyklus bildet.
Das Bild zeigt auch, dass trotz einer asymmetrisch wechselnden Last die minimalen Spalthöhen in beide Richtungen fast gleich sind. Das liegt daran, dass sich in der oberen Lagerhälfte eine Schmiertasche befindet, die den Aufbau eines geschlossenen Druckberges beeinträchtigt und so die Tragfähigkeit verringert. Das ist auch gut in der Animation zu Bild 4.071 zu beobachten.
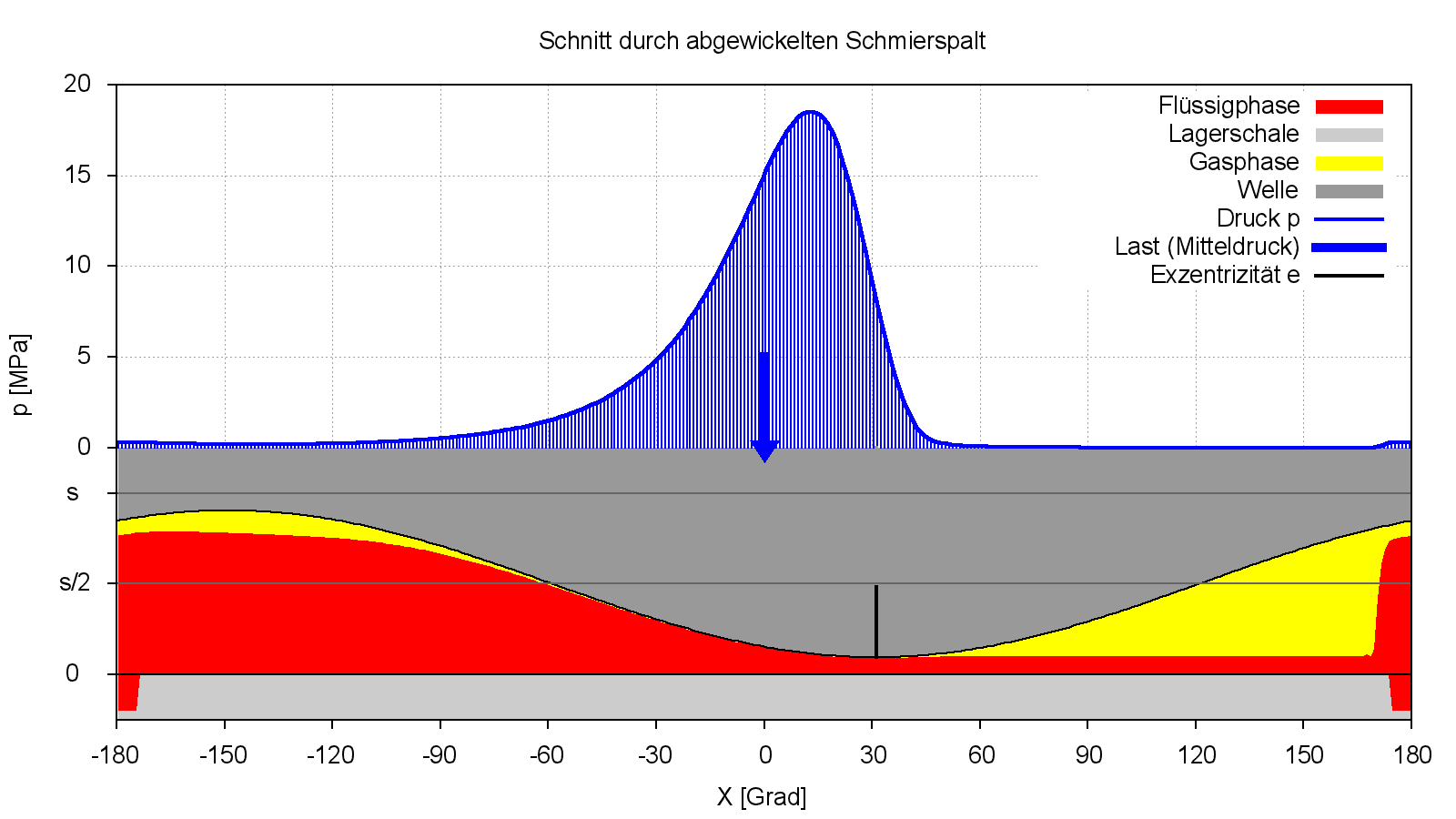
Die Bilder 4.073 und 4.074 zeigen die Druckverteilung p, die Spaltgeometrie h und die Verteilung der Schmierflüssigkeit hF über den abgewickelten Schmierspalt für den Zeitpunkt JT=226 der maximalen Lagerbelastung in der 2.Wellenumdrehung. Die zugehörigen Animationen zeigen den Verlauf dieser Parameter über den Zeitraum der 2.Wellenumdrehung JT=181 bis 361.
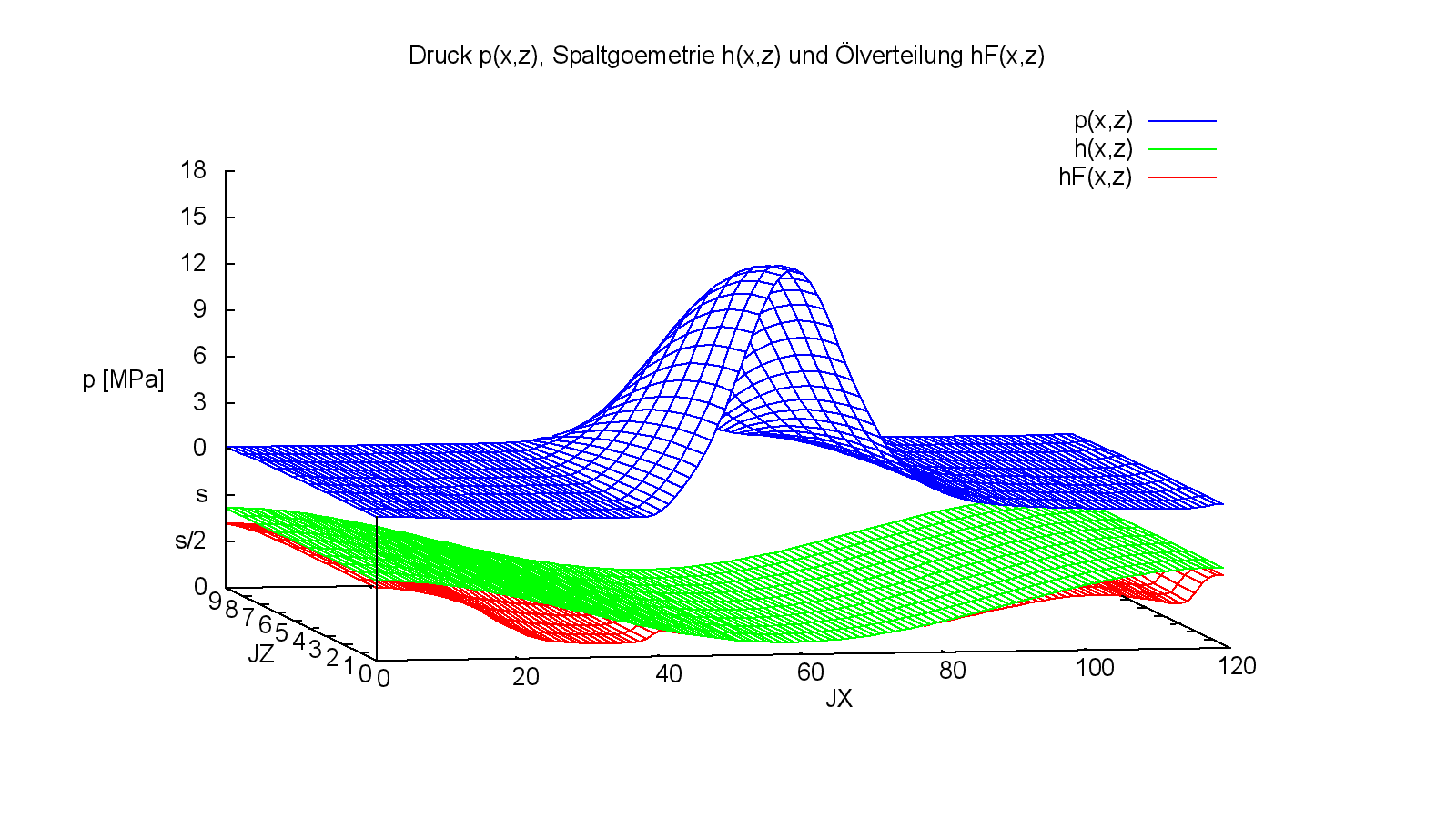
Bild 4.073: Druckverteilung p, Spaltgeometrie h und Flüssigkeitsverteilung hF zum Zeitpunkt der maximalen Belastung des Demonstrationsbeispiels Demo05 (Bilddatei: Demo05-Dim-3d-Abw-p-h-hF-JT=226.png) (Animation: Demo.Demo05-Dim-3d-Abw-p-h-hF)

Bild 4.074: Druckverteilung p, Spaltgeometrie h und Flüssigkeitsverteilung hF in Lagermitte zum Zeitpunkt der maximalen Belastung des Demonstrationsbeispiels Demo05 (Bilddatei: Demo05-Dim-2d-Abw-p-h-hF-JT=226-JZ=1.png) (Animation: Demo05-Dim-2d-Abw-p-h-hF-JZ=1.wmv)
Demonstrationsbeispiel Demo05-1:
Aus dem Demonstrationsbeispiel Demo05 wurde das Beispiel Demo05-1 abgeleitet. Hier wurde lediglich die Zeitschrittweite t verdoppelt und so eine Instabilität provoziert. Die Problematik von Instabilitäten wird ausführlich im Abschnitt 4.9.2 beschrieben.
zurück weiterDie primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo06.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Reynoldssche Dgl. mit "Guembelscher Randbedingung" (Theo = 1) -2- Belastung des Lagers vorgegeben (Last = 2) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale ideal zylindrisch und starr (Schale = 1) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Die Angaben des folgenden Hauptmenüs beschreiben das periphere Schmiermittelversorgungssystem sowohl qualitativ als auch quantitativ:
----------------------------------------------------------------------
Universal-Schmiermittel-Versorgungssystem
----------------------------------------------------------------------
NPu = 1 Anzahl der Schmiermittelpumpe
NTa = 5 Anzahl der Schmiertaschen
NVe = 5 Anzahl der Verbindungsleitungen
NVar= 1 Anzahl der Geraetevarianten
P u m p e n :
max.Pumpendruck max. Oelstrom
JPu pPuMax(JPu) qPuMax(JPu)
1 16.0000 MPa 5.0000 L/min
G e r a e t e v a r i a n t e n in den Verbindungsleitungen:
1 Nur Kapillare bzw. Leitungswiderstand
1 1 ccp =10000.0000 mm^-3 Widerstandsbeiwert
V e r b i n d u n g s l e i t u n g e n :
JVe Nummer der Verbindungsleitung
JPu Nummer der verbundenen Pumpe
JVar Nummer der Geraetevariante in der Leitung
JTa Nummer der verbundenen Schmiertasche
Typ Nummer des Geraetetyps
JVe JPu JVar JTa Typ Bezeichnung des Geraetetyps
1 1 >-- 1--< 1 1 Nur Kapillare bzw. Leitungswiderstand
2 1 >-- 1--< 2 1 Nur Kapillare bzw. Leitungswiderstand
3 1 >-- 1--< 3 1 Nur Kapillare bzw. Leitungswiderstand
4 1 >-- 1--< 4 1 Nur Kapillare bzw. Leitungswiderstand
5 1 >-- 1--< 5 1 Nur Kapillare bzw. Leitungswiderstand
Bei diesem Lager handelt es sich um ein klassisches hydrostatisches Lager, bei dem die Schmiermittelverteilung auf die einzelnen Schmiertaschen durch einfache Laminardrosseln (Kapillaren) erfolgt. Im Programm ist nur der Widerstandsbeiwert der Laminardrossel gefragt. Mit welchen Parametern (Innendurchmesser und Länge) dieser Wert realisiert wird, muss der Anwender selbst festlegen. Der Widerstandsbeiwert ccp=10 000 mm-3 ist z.B. mit einer Kapillare mit einem Innendurchmesser von 0,5 mm und einer Länge von 150 mm realisierbar. Dazu wird empfohlen eine kleine Kalkulationstabelle anzulegen. So kann man schnell geeignete Werte ermitteln und bekommt ein Gefühl für die Abmessungen erforderlicher Kapillaren. Die Formeln dazu siehe Abschnitt 2.1.6.2.1 und 2.2.6.2.1.
Die Berechnungen erfolgen hier sinnvollerweise mit der klassischen Reynoldsschen DGL (Theo=1), weil es bei dieser Lagervariante kein Unterdruckgebiet mit Kavitation gibt und deshalb die aufwendigere Berechnung mit der erweiterten Reynoldsschen DGL (Theo=2) nicht erforderlich ist.
Die nachfolgenden Bilder 4.076 und 4.077 zeigen einige Darstellungsmöglichkeiten der Ergebnisse.
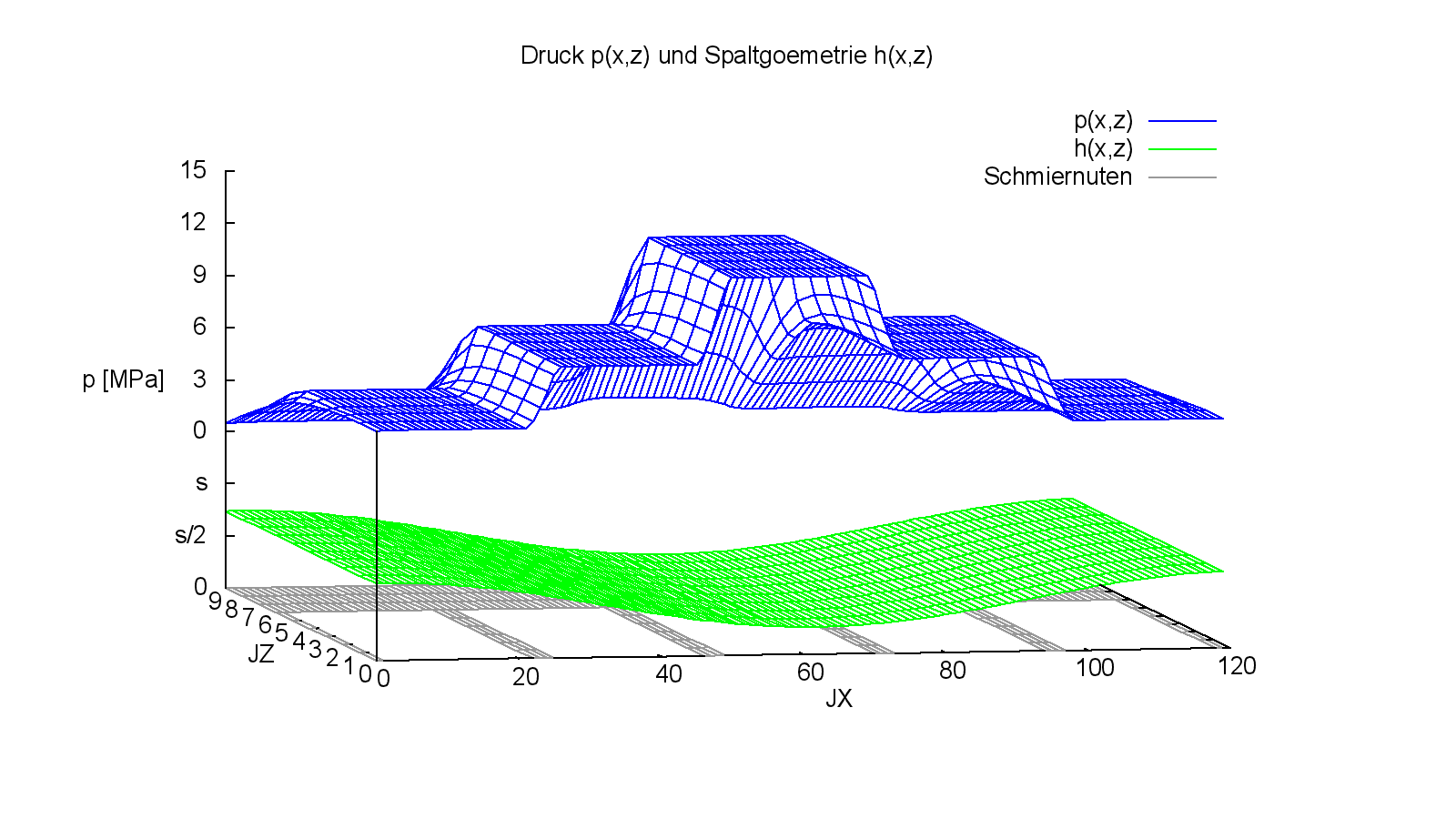
Bild 4.076: Druckverteilung p und Spaltgeometrie h im stationären Zustand des Demonstrationsbeispiels Demo06 (Bilddatei: Demo06-Dim-3d-Abw-p-h-Nut-JT=21.png)
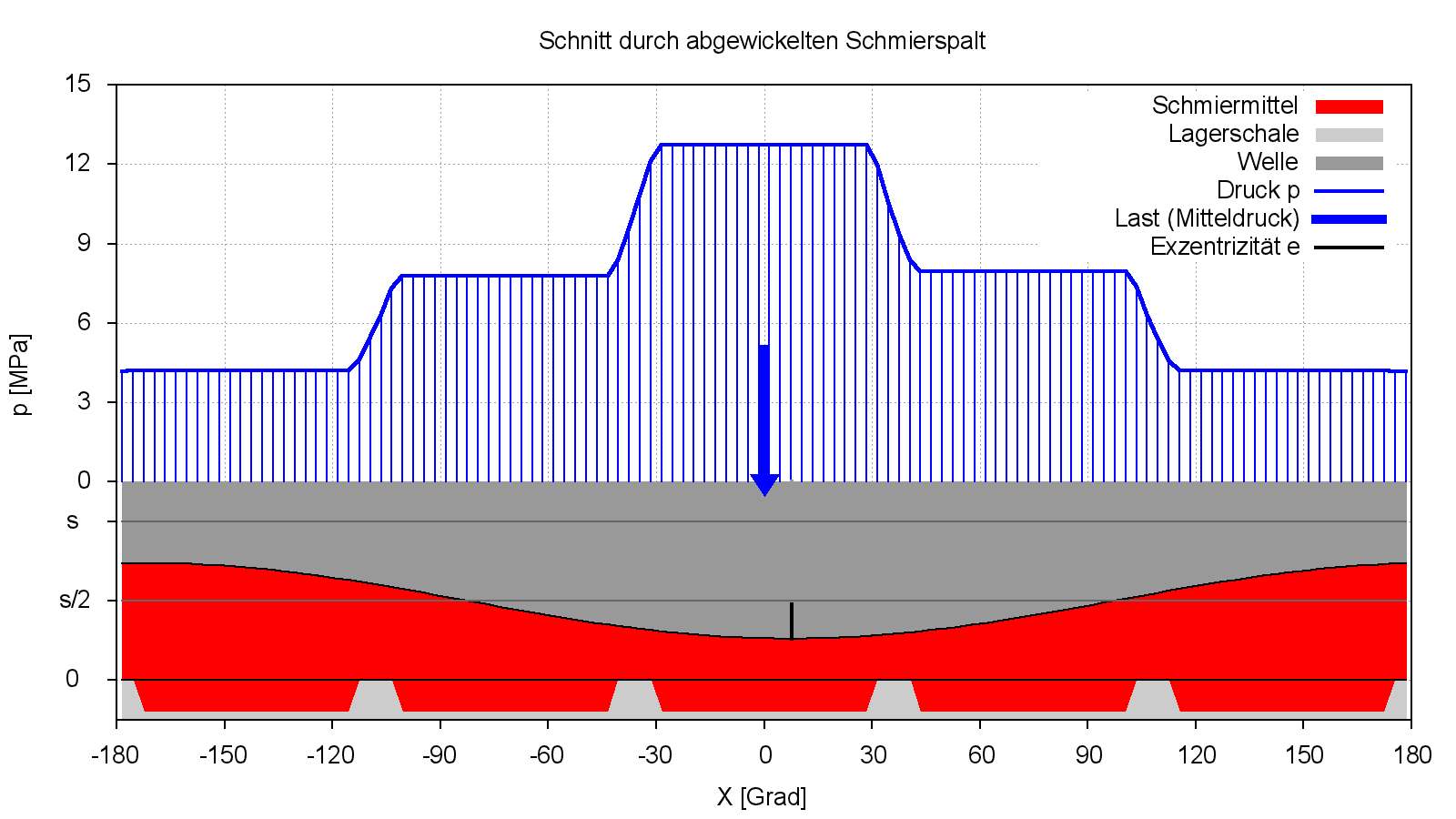
In diesem Beispiel wurde eine Wellendrehzahl von 500 U/min berücksichtigt. Wie die fast vollständige Symmetrie der Druckverteilung zeigt, handelt es sich bei diesem Beispiel um ein klassisches hydrostatisches Lager, bei dem hydrodynamische Einflüsse und damit auch die Wellendrehzahl kaum eine Rolle spielen. Bei der Drehzahl von 0 U/min würde sich die Tragfähigkeit deshalb kaum ändern.
Das Programm liefert als Ergebnis auch die Schmiermittelströme durch das Lager, das Wellenreibmoment und die Energiebilanz des Schmierspalts durch die Aktion -46- im PostProzessor.
Oelstrom- und Leistungsbilanz am Schmierspalt zum Zeitpunkt JT= 21
============================================================================
NTa = 5 Anzahl der Schmiertaschen im Lager
============================================================================
S c h m i e r t a s c h e n
----------------------------------------------------------------------------
JTa Nummer der Schmiertasche
pTa Druck in der Schmiertasche
qTa Oelstrom von den Verbindungsleitungen in die Schmiertasche
leiTa Leistung des Oelstroms in die Schmiertasche
JTa pTa qTa leiTa
[MPa] [L/min] [kW]
1 4.2196 0.7068 0.0497
2 7.7770 0.4934 0.0640
3 12.7433 0.1954 0.0415
4 7.9503 0.4830 0.0640
5 4.1950 0.7083 0.0495
----------------------------------------------------------------------------
Summe 2.5869 0.2687
============================================================================
S t r o m b i l a n z
----------------------------------------------------------------------------
Summe qTa 2.5869 L/min ueber die Schmiertaschen zufliessender Oelstrom
-qRand -2.6521 L/min ueber Lagerrand abfliessender Oelstrom
----------------------------------------------------------------------------
=volSpalt_t 0.0000 L/min =dvolSpalt/dt Spaltvolumenaenderung
Differenz -0.0652 L/min =(Summe pTa)-qRand-d(volSpalt*FGes)/dt
rel.Differenz -2.52 % =Differenz/(summe qTa)*100
============================================================================
S p a l t v o l u m e n
----------------------------------------------------------------------------
volSpalt 0.7854 qcm Schmierspaltvolumen
============================================================================
R e i b m o m e n t
----------------------------------------------------------------------------
moWe 2.3771 Nm Reibmoment an der Welle
============================================================================
E n e r g i e b i l a n z
----------------------------------------------------------------------------
Summe leiTa 0.2687 kW in die Schmiertaschen zugefuehrte Leistung
-leiRand 0.0000 kW ueber Lagerrand abfliessende Leistung
+leiWe 0.1245 kW durch Reibmoment zugefuehrte mech. Leistung
----------------------------------------------------------------------------
=lreib 0.3993 kW im Schmierspalt in Waerme umgewandelte Leistung
Differenz -0.0062 kW =(Summe leiTa)-leiRand+leiWe-lreib
rel.Differenz -1.55 % =Differenz/lreib*100
============================================================================
Das Programm liefert als Ergebnis auch die Schmiermittelströme durch das Schmiermittel-Versorgungssystem und die zugehörige Energiebilanz für die Auslegung des peripheren Schmiermittel-Versorgungssystems durch die Aktion -47- im PostProzessor:
Daten des peripheren Schmiersystems zum Zeitpunkt JT= 21
============================================================================
NPu = 1 Anzahl der Schmiermittelpumpen
NTa = 5 Anzahl der Schmiertaschen im Lager
NVe = 5 Anzahl Verbindungsleitungen zwischen Pumpen und Schmiertaschen
NVar= 1 Anzahl der Geraetevarianten in den Verbindungsleitungen
============================================================================
P u m p e n
----------------------------------------------------------------------------
JPu Nummer der Pumpe
pPuMax maximaler Pumpendruck, durch Sicherheitsventil begrenzt
pPu aktueller Pumpendruck
qPuMax maximaler Pumpenoelstrom
qPu aktuell fuer die Schmierung genutzter Pumpenoelstrom
qPuVer ueber das Sicherheitsventil abgefuehrter Oelstrom
leiPuMax installierte (maximale moegliche) Pumpenleistung
leiPu aktuelle Pumpenleistung
leiPuVer Verlustleistung des ueber das Sicherheitsventil abgefuehrten Oelstroms
JPu pPuMax pPu qPuMax qPu qPuVer leiPuMax leiPu leiPuVer
[MPa] [MPa] [L/min] [L/min] [L/min] [kW] [kW] [kW]
1 16.0000 16.0000 5.0000 2.5869 2.4131 1.3333 1.3333 0.6435
----------------------------------------------------------------------------
Summe 5.0000 2.5869 2.4131 1.3333 1.3333 0.6435
============================================================================
G e r a e t e v a r i a n t e n in den Verbindungsleitungen:
----------------------------------------------------------------------------
1 Nur Kapillare bzw. Leitungswiderstand
1 1 ccp =10000.0000 mm^-3 Widerstandsbeiwert
============================================================================
V e r b i n d u n g s l e i t u n g e n
----------------------------------------------------------------------------
JVe Nummer der Verbindungsleitung
pVeVer Druckgefaelle von der Pumpe zur Schmiertasche
qVe Oelstrom durch die Verbindungsleitung
leiVeVer Verlustleistung in der Verbindungsleitung
JPu Nummer der verbundenen Pumpe
JVar Nummer der Geraetevariante in der Leitung
JTa Nummer der verbundenen Schmiertasche
JVe pVeVer qVe leiVeVer JPu JVar JTa Bezeichnung des Geraetetyps
[MPa] [L/min] [kW]
1 11.7804 0.7068 0.1388 1 >-- 1--< 1 Nur Kapillare bzw. Leitungswiderstand
2 8.2231 0.4934 0.0676 1 >-- 1--< 2 Nur Kapillare bzw. Leitungswiderstand
3 3.2568 0.1954 0.0106 1 >-- 1--< 3 Nur Kapillare bzw. Leitungswiderstand
4 8.0495 0.4830 0.0648 1 >-- 1--< 4 Nur Kapillare bzw. Leitungswiderstand
5 11.8050 0.7083 0.1394 1 >-- 1--< 5 Nur Kapillare bzw. Leitungswiderstand
----------------------------------------------------------------------------
Summe 2.5869 0.4212
============================================================================
S t r o m b i l a n z
----------------------------------------------------------------------------
Summe qPuMax 5.0000 L/min Bereitgestellter Pumpenstrom (Konstantpumpen)
-Summe qPuVer -2.4131 L/min Ueber Druckbegrenzungsventil abgefuehrter Oelstrom
----------------------------------------------------------------------------
=Summe qPu 2.5869 L/min in den Schmierspalt gepumpter Oelstrom
=Summe qVe 2.5869 L/min -"-
=Summe qTa 2.5869 L/min -"-
============================================================================
E n e r g i e b i l a n z
----------------------------------------------------------------------------
Summe leiPuMax 1.3333 kW Summe der installierten Pumpenleistungen
----------------------------------------------------------------------------
Summe leiPu 1.3333 kW Summe der aktuellen Pumpenleistung
-Summe leiPuVer -0.6435 kW Ueber Druckbegrenzungsventil abgefuehrte Leistung
----------------------------------------------------------------------------
=Summe leiVe 0.6898 kW in die Verbindungsleitungen zugefuehrte Leistungen
-Summe leiVeVer -0.4212 kW Reibleistungsverluste in den Verbindungsleitungen
----------------------------------------------------------------------------
=Summe leiTa 0.2687 kW in die Schmiertaschen zugefuehrte Leistung
============================================================================
Zusammenfassend kann aus der umfangreichen Tabelle über die Schmiermittelströme und die Energiebilanzen entnommen werden, dass das Lager im vorgegebenen Betriebszustand einen Schmiermittelstrom von 2,6 l/min bei 16 MPa Zuführdruck benötigt.
Damit wird dem Lager eine hydraulische Leistung von 0,69 kW zugeführt, von der in den Kapillaren bereits 0,42 kW in Wärme umgewandelt werden. Zusätzlich wird dem Lager bei einem Reibmoment von 2,4 Nm eine Reibleistung von 0,12 kW zugeführt.
zurück weiterDie primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo07.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:

Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Reynoldssche Dgl. mit "Guembelscher Randbedingung" (Theo = 1) -2- Belastung des Lagers vorgegeben (Last = 2) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale ideal zylindrisch und starr (Schale = 1) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Die Angaben des folgenden Hauptmenüs beschreiben das periphere Schmiermittelversorgungssystem sowohl qualitativ als auch quantitativ:
----------------------------------------------------------------------
Universal-Schmiermittel-Versorgungssystem
----------------------------------------------------------------------
NPu = 1 Anzahl der Schmiermittelpumpe
NTa = 5 Anzahl der Schmiertaschen
NVe = 5 Anzahl der Verbindungsleitungen
NVar= 1 Anzahl der Geraetevarianten
P u m p e n :
max.Pumpendruck max. Oelstrom
JPu pPuMax(JPu) qPuMax(JPu)
1 16.0000 MPa 5.0000 L/min
G e r a e t e v a r i a n t e n in den Verbindungsleitungen:
1 Nur PM-Regler
1 1 q0 = 0.1300 L/min Oelstrom durch Regler bei Taschendruck PTa=0
1 2 qP = 0.2600 L/min Theoretischer Oelstrom bei Taschendruck PTa=PP
1 3 pP = 16.0000 MPa Pumpendruck bei Aufnahmen der Kennlinie
1 4 pS = 1.6000 MPa Differenz zwischen Pumpendruck PPu und Druck im Kennlinien-Scheitelpunkt S
1 5 eta0 = 100.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers bei Aufnahme der Kennlinie
1 6 eta1 = 100.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers im Betriebszustand
1 qP1 = 0.2600 L/min Theoretischer Oelstrom bei Taschendruck PTa=PPu
1 cpm = 0.0081 L/min/MPa Anstieg der Kennlinie im aufsteigenden Ast
1 rpm = 6.4777 MPa*min/L Stroemungswiderstand des vollstaengig geoeffneten PM-Reglers
V e r b i n d u n g s l e i t u n g e n :
JVe Nummer der Verbindungsleitung
JPu Nummer der verbundenen Pumpe
JVar Nummer der Geraetevariante in der Leitung
JTa Nummer der verbundenen Schmiertasche
Typ Nummer des Geraetetyps
JVe JPu JVar JTa Typ Bezeichnung des Geraetetyps
1 1 >-- 1--< 1 3 Nur PM-Regler
2 1 >-- 1--< 2 3 Nur PM-Regler
3 1 >-- 1--< 3 3 Nur PM-Regler
4 1 >-- 1--< 4 3 Nur PM-Regler
5 1 >-- 1--< 5 3 Nur PM-Regler
Gegenüber dem klassischen hydrostatischen Lager mit Laminardrosseln kann mit Progressiv-Mengen-Reglern (PM-Regler siehe Abschnitt 2.1.6.2.3) in den Schmiermittel-Verteilungsleitungen erheblich Schmiermittelstrom und damit hydraulische Energie gespart werden. Das Lager des Demonstrationsbeispiels Demo07 hat die gleichen Abmessungen, das gleiche Lagerspiel und die gleiche Lagerbelastung wie das Demonstrationsbeispiel Demo06. Nur die Laminardrosseln wurden gegen PM-Regler ausgetauscht. Die Parameter der PM-Regler wurden so gewählt, dass bei der vorgegebenen Lagerbelastung die gleiche Exzentrizität der Welle auftritt.
Die nachfolgenden Bilder 4.079 und 4.080 zeigen einige Darstellungsmöglichkeiten der Ergebnisse.
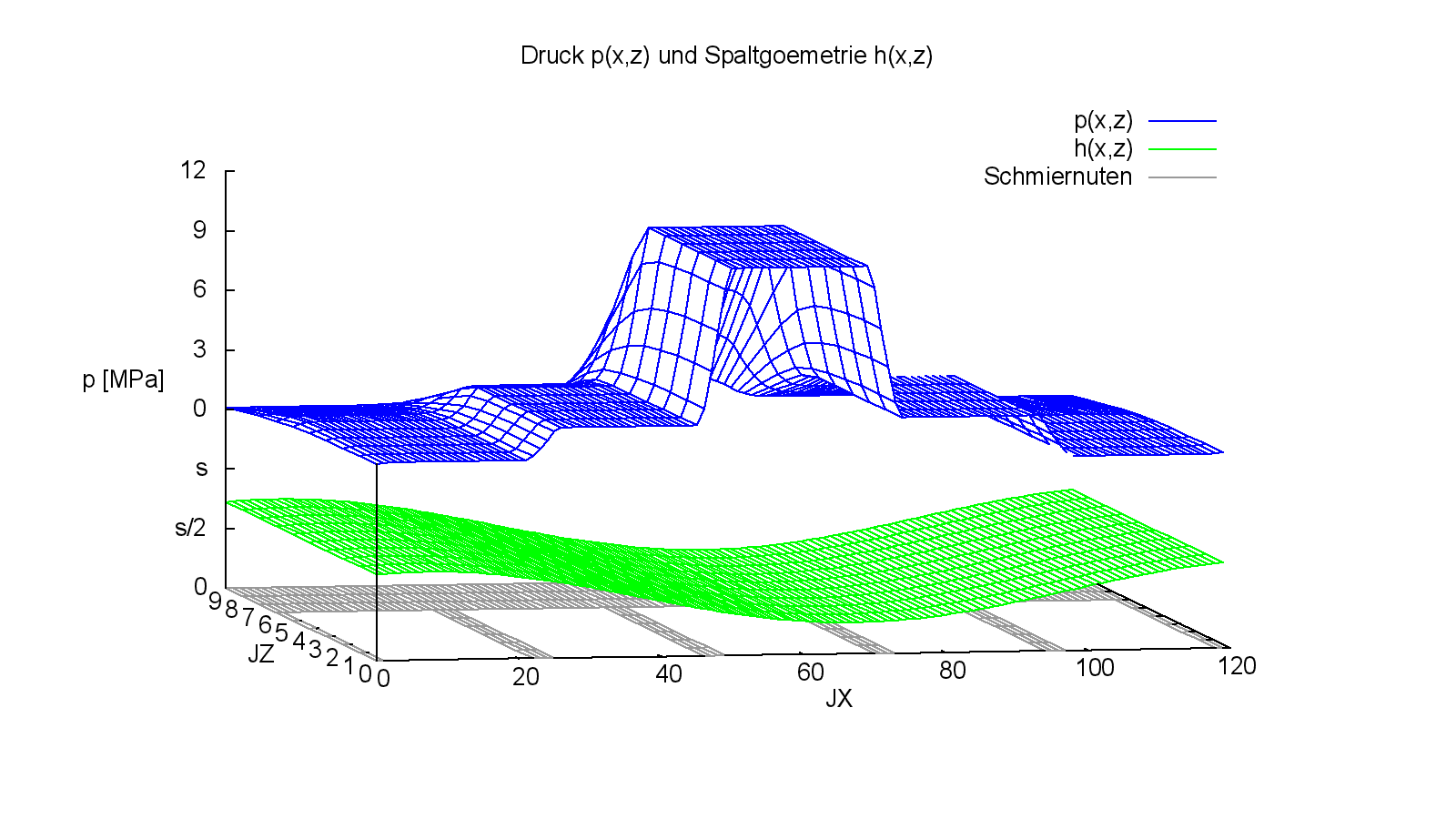

Das Programm liefert als Ergebnis auch die Schmiermittelströme durch das Lager, das Wellenreibmoment und die Energiebilanz des Lagers für die Auslegung des peripheren Schmiermittel-Versorgungssystems.
Oelstrom- und Leistungsbilanz am Schmierspalt zum Zeitpunkt JT= 21
============================================================================
NTa = 5 Anzahl der Schmiertaschen im Lager
============================================================================
S c h m i e r t a s c h e n
----------------------------------------------------------------------------
JTa Nummer der Schmiertasche
pTa Druck in der Schmiertasche
qTa Oelstrom von den Verbindungsleitungen in die Schmiertasche
leiTa Leistung des Oelstroms in die Schmiertasche
JTa pTa qTa leiTa
[MPa] [L/min] [kW]
1 0.9619 0.1378 0.0022
2 2.5807 0.1510 0.0065
3 10.5014 0.2153 0.0377
4 2.8341 0.1530 0.0072
5 0.7621 0.1362 0.0017
----------------------------------------------------------------------------
Summe 0.7933 0.0553
============================================================================
S t r o m b i l a n z
----------------------------------------------------------------------------
Summe qTa 0.7933 L/min ueber die Schmiertaschen zufliessender Oelstrom
-qRand -0.8172 L/min ueber Lagerrand abfliessender Oelstrom
----------------------------------------------------------------------------
=volSpalt_t 0.0000 L/min =dvolSpalt/dt Spaltvolumenaenderung
Differenz -0.0239 L/min =(Summe pTa)-qRand-d(volSpalt*FGes)/dt
rel.Differenz -3.01 % =Differenz/(summe qTa)*100
============================================================================
S p a l t v o l u m e n
----------------------------------------------------------------------------
volSpalt 0.7854 qcm Schmierspaltvolumen
============================================================================
R e i b m o m e n t
----------------------------------------------------------------------------
moWe 2.4568 Nm Reibmoment an der Welle
============================================================================
E n e r g i e b i l a n z
----------------------------------------------------------------------------
Summe leiTa 0.0553 kW in die Schmiertaschen zugefuehrte Leistung
-leiRand 0.0000 kW ueber Lagerrand abfliessende Leistung
+leiWe 0.1286 kW durch Reibmoment zugefuehrte mech. Leistung
----------------------------------------------------------------------------
=lreib 0.1854 kW im Schmierspalt in Waerme umgewandelte Leistung
Differenz -0.0014 kW =(Summe leiTa)-leiRand+leiWe-lreib
rel.Differenz -0.74 % =Differenz/lreib*100
============================================================================
Daten des peripheren Schmiersystems zum Zeitpunkt JT= 21
============================================================================
NPu = 1 Anzahl der Schmiermittelpumpen
NTa = 5 Anzahl der Schmiertaschen im Lager
NVe = 5 Anzahl Verbindungsleitungen zwischen Pumpen und Schmiertaschen
NVar= 1 Anzahl der Geraetevarianten in den Verbindungsleitungen
============================================================================
P u m p e n
----------------------------------------------------------------------------
JPu Nummer der Pumpe
pPuMax maximaler Pumpendruck, durch Sicherheitsventil begrenzt
pPu aktueller Pumpendruck
qPuMax maximaler Pumpenoelstrom
qPu aktuell fuer die Schmierung genutzter Pumpenoelstrom
qPuVer ueber das Sicherheitsventil abgefuehrter Oelstrom
leiPuMax installierte (maximale moegliche) Pumpenleistung
leiPu aktuelle Pumpenleistung
leiPuVer Verlustleistung des ueber das Sicherheitsventil abgefuehrten Oelstroms
JPu pPuMax pPu qPuMax qPu qPuVer leiPuMax leiPu leiPuVer
[MPa] [MPa] [L/min] [L/min] [L/min] [kW] [kW] [kW]
1 16.0000 16.0000 5.0000 0.7933 4.2067 1.3333 1.3333 1.1218
----------------------------------------------------------------------------
Summe 5.0000 0.7933 4.2067 1.3333 1.3333 1.1218
============================================================================
G e r a e t e v a r i a n t e n in den Verbindungsleitungen:
----------------------------------------------------------------------------
1 Nur PM-Regler
1 1 q0 = 0.1300 L/min Oelstrom durch Regler bei Taschendruck PTa=0
1 2 qP = 0.2600 L/min Theoretischer Oelstrom bei Taschendruck PTa=PP
1 3 pP = 16.0000 MPa Pumpendruck bei Aufnahmen der Kennlinie
1 4 pS = 1.6000 MPa Differenz zwischen Pumpendruck PPu und Druck im Kennlinien-Scheitelpunkt S
1 5 eta0 = 100.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers bei Aufnahme der Kennlinie
1 6 eta1 = 100.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers im Betriebszustand
============================================================================
V e r b i n d u n g s l e i t u n g e n
----------------------------------------------------------------------------
JVe Nummer der Verbindungsleitung
pVeVer Druckgefaelle von der Pumpe zur Schmiertasche
qVe Oelstrom durch die Verbindungsleitung
leiVeVer Verlustleistung in der Verbindungsleitung
JPu Nummer der verbundenen Pumpe
JVar Nummer der Geraetevariante in der Leitung
JTa Nummer der verbundenen Schmiertasche
JVe pVeVer qVe leiVeVer JPu JVar JTa Bezeichnung des Geraetetyps
[MPa] [L/min] [kW]
1 15.0381 0.1378 0.0345 1 >-- 1--< 1 Nur PM-Regler
2 13.4193 0.1510 0.0338 1 >-- 1--< 2 Nur PM-Regler
3 5.4986 0.2153 0.0197 1 >-- 1--< 3 Nur PM-Regler
4 13.1659 0.1530 0.0336 1 >-- 1--< 4 Nur PM-Regler
5 15.2379 0.1362 0.0346 1 >-- 1--< 5 Nur PM-Regler
----------------------------------------------------------------------------
Summe 0.7933 0.1562
============================================================================
S t r o m b i l a n z
----------------------------------------------------------------------------
Summe qPuMax 5.0000 L/min Bereitgestellter Pumpenstrom (Konstantpumpen)
-Summe qPuVer -4.2067 L/min Ueber Druckbegrenzungsventil abgefuehrter Oelstrom
----------------------------------------------------------------------------
=Summe qPu 0.7933 L/min in den Schmierspalt gepumpter Oelstrom
=Summe qVe 0.7933 L/min -"-
=Summe qTa 0.7933 L/min -"-
============================================================================
E n e r g i e b i l a n z
----------------------------------------------------------------------------
Summe leiPuMax 1.3333 kW Summe der installierten Pumpenleistungen
----------------------------------------------------------------------------
Summe leiPu 1.3333 kW Summe der aktuellen Pumpenleistung
-Summe leiPuVer -1.1218 kW Ueber Druckbegrenzungsventil abgefuehrte Leistung
----------------------------------------------------------------------------
=Summe leiVe 0.2116 kW in die Verbindungsleitungen zugefuehrte Leistungen
-Summe leiVeVer -0.1562 kW Reibleistungsverluste in den Verbindungsleitungen
----------------------------------------------------------------------------
=Summe leiTa 0.0553 kW in die Schmiertaschen zugefuehrte Leistung
============================================================================
Ein Vergleich der wesentlichen energetischen Parameter des Lagers mit PM-Reglern (Demo07) mit dem Lager mit Kapillaren (Demo06) bei sonst gleichen Bedingungen zeigt nachfolgende Tabelle 4.14.
Tabelle 4.14: Energetischer Vergleich eines hydrostatischen Lagers mit Laminardrosseln und mit Progressiv-Mengen-Reglern
| Parameter | Maßeinheit | Kapillare | PM-Regler | Bezeichnung |
| Summe qTa | L/min | 2,59 | 0,79 | durch das Lager gepumpter Schmiermittelstrom |
| Summe leiVe | kW | 0,69 | 0,21 | dem Lager zugeführte hydraulische Leistung |
| Summe leiVever | kW | 0,42 | 0,15 | davon in den Kapillaren bzw. den PM-Reglern in Wärme umgewandelte Leistung |
| Summe leiTa | kW | 0,27 | 0,06 | davon im Schmierspalt in Wärme umgewandelte Leistung |
| moWe | Nm | 2,4 | 2,5 | Wellenreibmoment |
| leiWe | kW | 0,12 | 0,13 | Leistung des Wellenreibmoments |
| kW | 0,71 | 0,34 | Gesamtleistung, die im Lager in Wärme umgewandelt wird = leiWe + Summe leiVe |
Das Beispiel zeigt, dass durch die PM-Regler ca. 50% Energie am Lager eingespart werden kann. Hinzu kommt, dass diese eingesparte Leistung auch nicht wieder weggekühlt werden muss.
zurück weiterDie primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo08.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
----------------------------------------------------------------------
Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp
----------------------------------------------------------------------
-1- Reynoldssche Dgl. mit "Guembelscher Randbedingung" (Theo = 1)
-2- Belastung des Lagers vorgegeben (Last = 2)
-3- Vollstaendig umschlossenes Lager (Vollum = 1)
-4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse)(Sym = 1)
-5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1)
-6- Gerade Welle (Biege = 1)
-7- Keine versetzten Lagerabschnitte (Versatz = 1)
-8- Welle ideal zylindrisch (Welle = 1)
-9- Lagerschale ideal zylindrisch und starr (Schale = 1)
-20- Evtl. einige Eingabeparameter zeitabhaengig (Dynamic = 2)
-21- Zeitschritte DT konstant (SchrittVar = 1)
-22- Omega konstant (OmegaVar = 1)
-24- f1(T)=f1Amp*sin(Omega1*T-Phi1)+f1Mit (LastVar = 5)
f2(T)=f2Amp*sin(Omega2*T-Phi2)+f2Mit
-30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Das Demonstrationsbeispiel "Demo08" ist weitgehend identisch mit dem Demonstrationsbeispiel "Demo07". Der einzige Unterschied besteht darin, dass jetzt ein wechselnder Belastungsverlauf vorgegeben ist. Es werden 2 Wellenumdrehungen berechnet. Die 1.Umdrehung ist die Anlaufrechnung. Mit der zweiten Umdrehung ergibt die Berechnung bereits bei einem geschlossenen Lastzyklus auch einen geschlossenen Zyklus der Welleverlagerungsbahn, was Bild 4.082 zeigt.

Bild 4.082: Verlagerungsbahn (rechts) während der Anlaufrechnung über 81 Zeitschritte bzw. 2 Wellenumdrehungen (Bilddatei: Demo08-Dim-2d-Pol-f-e-Punkte-JT=71.png) (Animation: Demo08-Dim-2d-Pol-f-e-Punkte.wmv)
Während das statische Bild 4.082 den Verlauf der Verlagerungsbahn für beide Wellendrehungen zeigt, also auch die Anlaufrechnung, wird in der zugehörigen Animation nur die 2.Wellenumdrehung dargestellt und es ist gut zu erkennen, dass die berechnete Verlagerungsbahn bereits einen geschlossenen Zyklus bildet.
Dass trotz eines symmetrischen Lastverlaufs die Verlagerungsbahn nicht auch symmetrisch ist, liegt daran, dass der hydrostatische Druckaufbau durch eine hydrodynamisch induzierte Schmiermittelströmung durch die Wellendrehung überlagert wird.
Die Bilder 4.083 und 4.084 zeigen die Druckverteilung p und die Spaltgeometrie h über den abgewickelten Schmierspalt für den Zeitpunkt JT=71 der nach oben gerichteten maximalen Lagerbelastung in der 2.Wellenumdrehung. Die zugehörigen Animationen zeigen den Verlauf dieser Parameter über den Zeitraum der 2.Wellenumgrehung JT=41 bis 81.
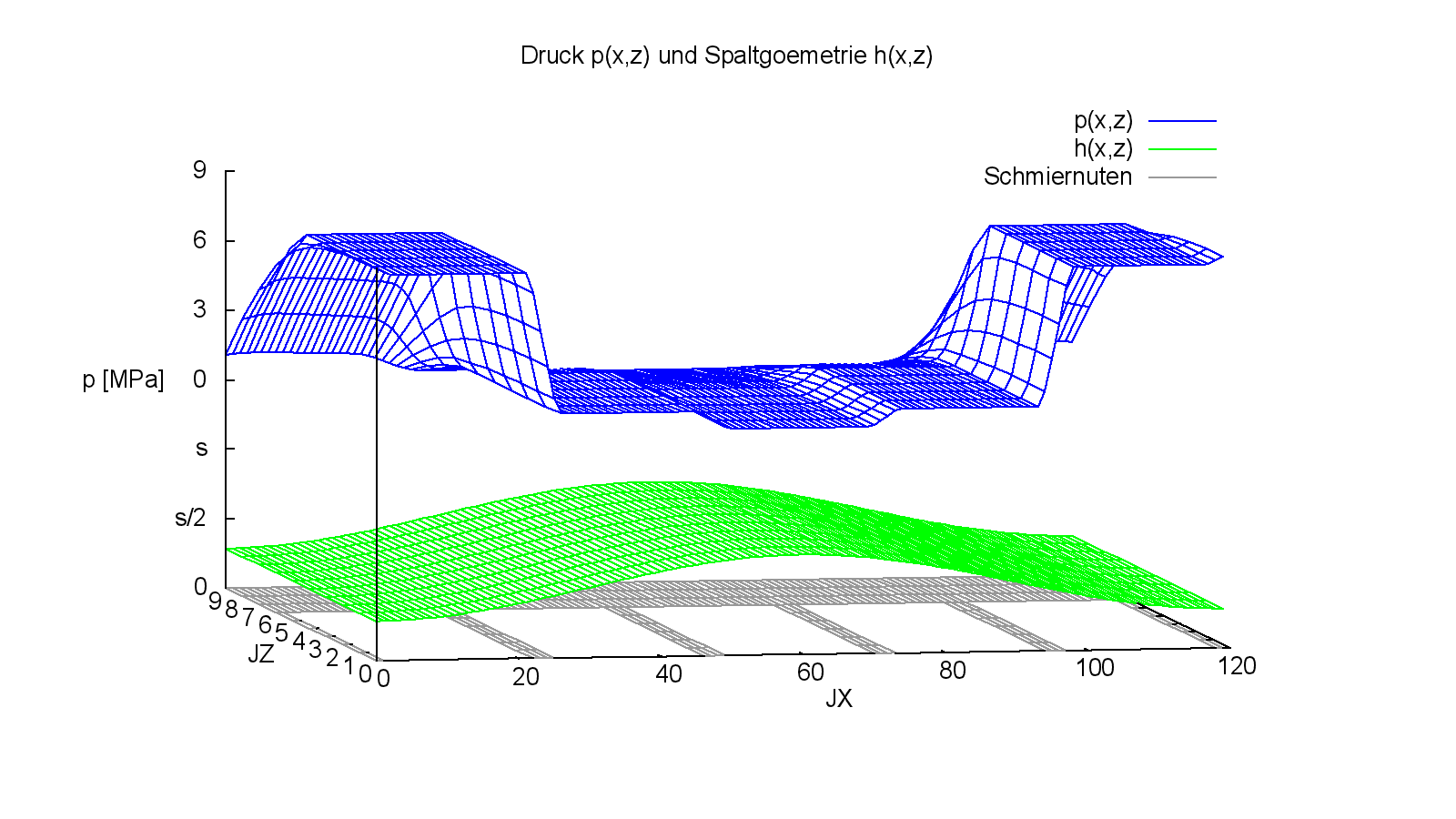
Bild 4.083: Druckverteilung p und Spaltgeometrie h zum Zeitpunkt der maximalen Belastung des Demonstrationsbeispiels Demo08 (Bilddatei: Demo08-Dim-3d-Abw-p-h-Nut-JT=71.png) (Animation: Demo08-Dim-3d-Abw-p-h-Nut.wmv)
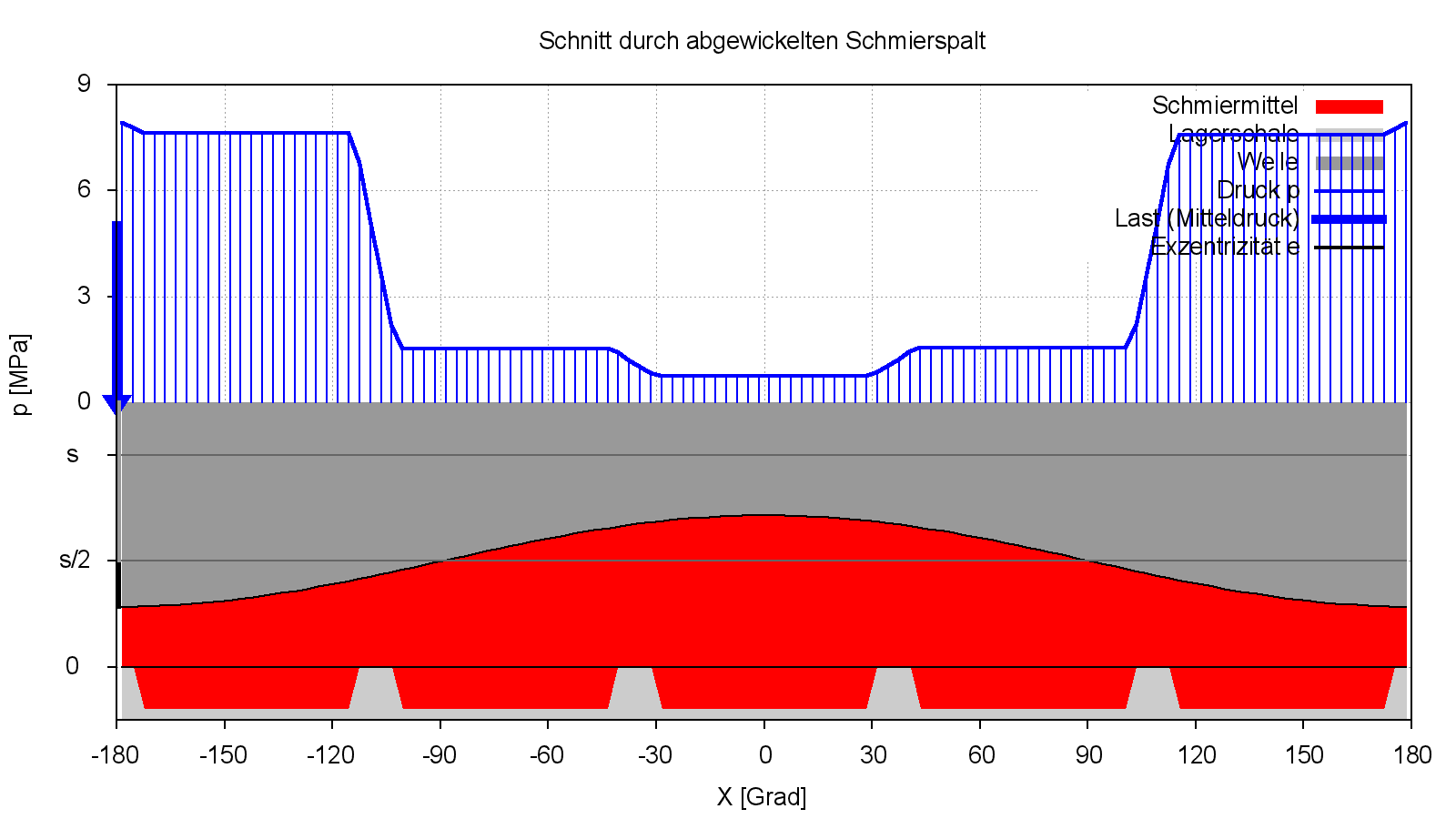
Bei hydrostatischen Lagern sind der erforderliche Schmiermittelstrom und die entsprechenden hydraulischen Leistungen, die das Lager in Wärme umwandelt von Interesse. Bild 4.085 zeigt im unteren Diagramm den Pumpenölstrom qPu, der dem Schmierspalt zugeführt wird. Im oberen Diagramm werden die Leistungen dargestellt, die dem Lager zugeführt und in Wärme verwandelt werden. Die Leistung leiWe ist die mechanische Leistung, die dem Lager über das Wellenreibmoment zugeführt wird. Die Leistung leiVeVer ist die Leistung, die infolge der Drosselwirkung bereits in den PM-Reglern in Wärme umgewandelt wird. Die Leistung leiTa wird über die Schmiertaschen direkt dem Schmierspalt zugeführt und durch die innere Reibung in dem Schmierspalt rund um die Schmiertaschen ebenfalls in Wärme umgewandelt. Die Summe aller drei Leistungen bildet den Gesamtenergieverbrauch des hydrostatischen Lagers. Wie das Beispiel zeigt, haben die PM-Regler hier den größten Anteil am Energieverbrauch des Lagers. Bei traditionellen Lagern mit Laminardrossel ist dieser Energieverbrauch aber noch wesentlich größer.
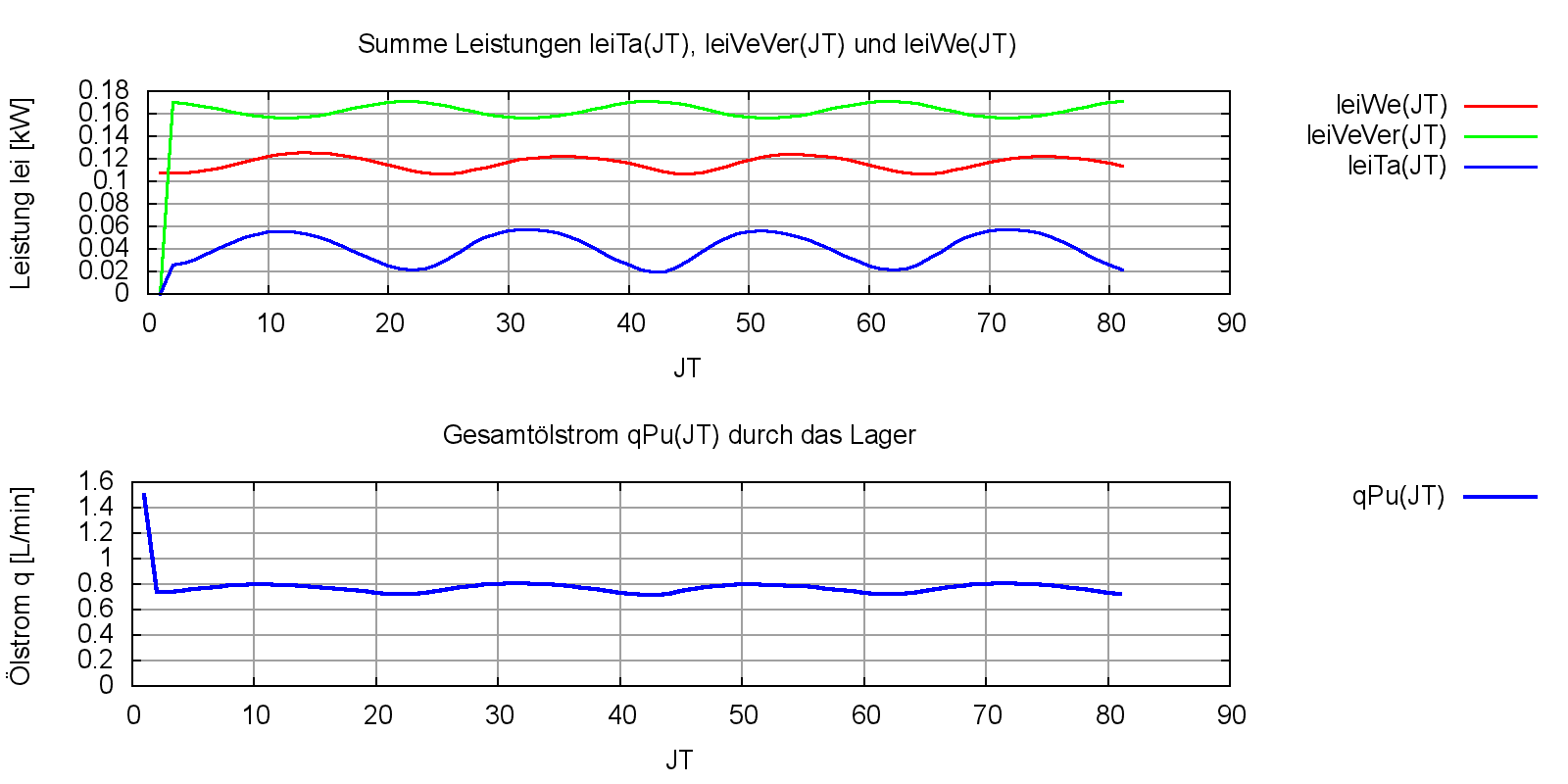
Bild 4.085: Leistungsaufnahme (oben) und Pumpenölstrom (unten) des instationär belasteten hydrostatischen Lagers des Demonstrationsbeispiels Demo08 über den berechneten Zeitraum von 2 Wellenumdrehungen (Bilddatei: Demo08-Dim-2d-Kart-lei-q-JT.png)
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo09.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Reynoldssche Dgl. mit "Guembelscher Randbedingung" (Theo = 1) -2- Belastung des Lagers vorgegeben (Last = 2) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale nur mit starrer punktw. geg. Formabweich. (Schale = 3) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Es können mit SIRIUS auch echte Mehrgleitflächenlager modelliert werden, allerdings nur solche mit festen Keilschuhen. Da es möglich ist, sich die unterschiedlichsten Formen und Anordnungen von Keilschuhen auszudenken und zu untersuchen, wurde im Programm SIRIUS darauf verzichtet, die Geometrie durch die Eingabe weniger Parameter fest einzuprogrammieren. Stattdessen ist für diesen Fall die Geometrie der Lagerschale durch eine Tabelle der punktweise gegebenen Formabweichungen von der idealzylindrischen Form einzugeben. Diese kann mit Hilfe einer Kalkulationstabelle z.B. mit Excel erzeugt werden. Bild 4.087 zeigt einen Ausschnitt der Textdatei "Demo09-Schale.txt", aus der die Geometrie der Lagerschale für das Demonstrationsbeispiel eingelesen wurde.
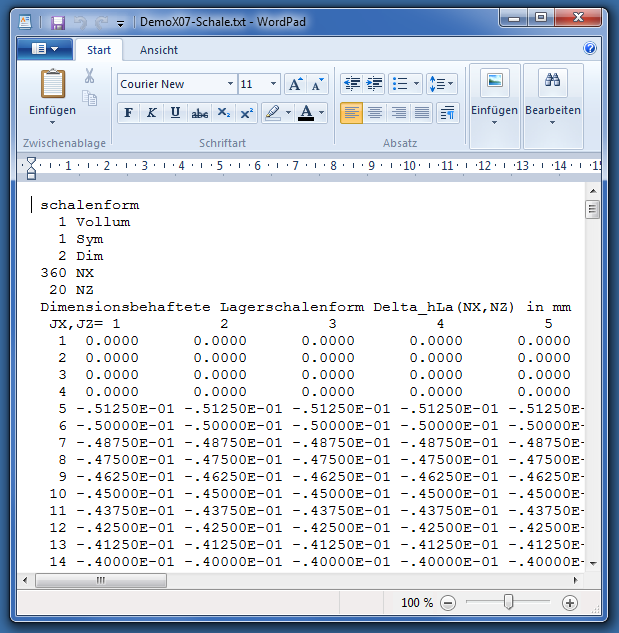
Bild 4.087: Linker oberer Ausschnitt der Tabelle der punktweise gegebenen Geometrie der Gleitschuhe des Mehrgleitflächenlagers für das Demonstrationsbeispiel Demo09 (Datei: Demo09-Schale.txt)
Die Bereiche der Lagerschale, wo sich aktuell kein Gleitschuh befindet, können aus der Berechnung ausgeschlossen werden, indem sie zu einer Schmiertasche erklärt werden, die alle Zwischenräume erfasst. Auch wenn diese Zwischenräume aus mehreren nicht zusammenhängenden Bereichen bestehen, können sie alle als eine einzige Schmiertasche modelliert werden. Die Erzeugung dieser Schmiertasche erfolgt im Hauptmenü: "Anordnung der Schmiertaschen festlegen" (siehe Abschnitt 4.4.8). Diese Schmiertasche muss dann mit einer Pumpe verbunden werden, die einen maximalen Schmiermitteldruck erzeugt, der gleich dem Umgebungsdruck des Lagers ist. Außerdem sollte diese Pumpe einen reichlichen Ölstrom erzeugen können, so dass die Pumpe durchgehend als druckgeregelte Pumpe arbeitet. Diese Maßnahme ist erforderlich, obwohl diese komplexe Schmiertasche an mehreren Stellen den Lagerrand berührt, weil das Programm bei direktem Kontakt von Schmiertasche und Lagerrand keinen Druckausgleich und keinen Flüssigkeitsaustausch vorsieht.
Im Demonstrationsbeispiel kann mit der klassischen Reynoldsschen Differentialgleichung gearbeitet werden (Theo=1), weil in den Gleitschuhen, aufgrund ihrer konkreten Form, nicht mit negativen Drücken im Schmierspalt zu rechnen ist.
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo09.txt" im Verzeichnis "./DatenDemo" abgelegt.
Wenn die Anlaufrechnung nicht von Interesse ist und nur das stationäre Endergebnis dokumentiert werden soll, ist, wie beim Demonstrationsbeispiel Demo01 (Abschnitt 4.8.1) beschrieben, zu verfahren. Für das Demonstrationsbeispiel Demo09 ist die verkürzte Dokumentation des stationären Endergebnisses in der Datei Demo09-1.txt abgelegt. Damit reduziert sich der erforderliche Speicherplatz von 3,7 MB auf 293 KB.
Nachfolgende Bilder zeigen einige Darstellungsmöglichkeiten der Ergebnisse.

Bild 4.088: Druckverteilung p und Spaltgeometrie h im stationären Zustand des Demonstrationsbeispiels Demo09 (Bilddatei: Demo09-Dim-3d-Abw-p-h-Nut-JT=41.png)
Die 3-d-Darstellung der Spalthöhe h(x,z) in Bild 4.088 ist nicht besonders anschaulich, weil hier der Eindruck entstehen könnte, dass die Keilschuhe an der Wellenoberfläche angeordnet sind, was prinzipiell auch möglich wäre. Anschaulicher ist hier die 2-d-Darstelung in Bild 4.089.
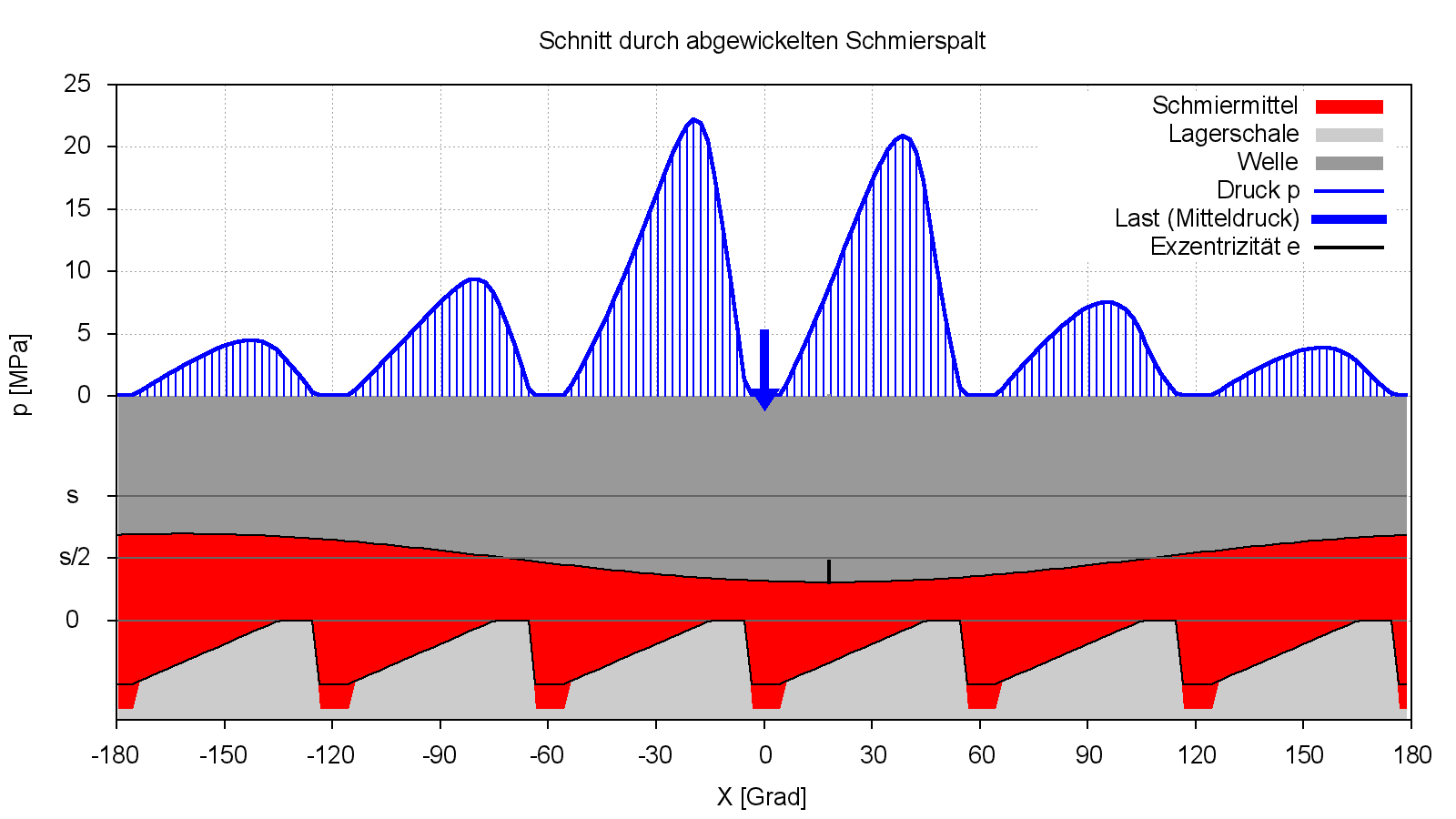
Bild 4.089: Druckverteilung p und Spaltgeometrie h in Lagermitte im stationären Zustand des Demonstrationsbeispiels Demo09 (Bilddatei: Demo09-Dim-2d-Abw-p-h-JT=41-JZ=1.png)

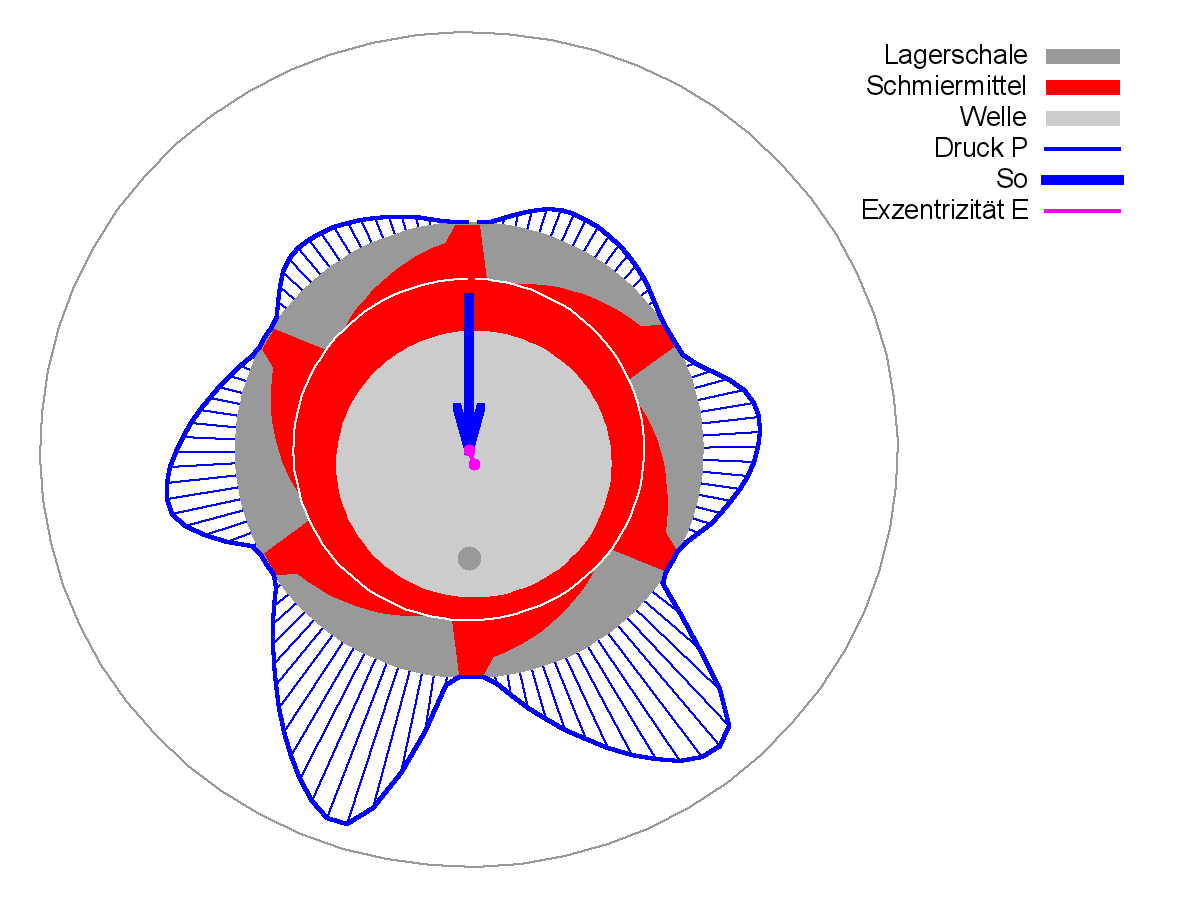
Bild 4.090: Lage der Wellenachse im Spielraum der Lagerschale zum stationären Betriebszustand (Bilddatei: Demo09-Dim-3d-Zyl-spiel-JT=41.png)
Bild 4.090 zeigt die Lage der Wellenachse (rot) im Spielraum (grün) des Lagers, der von den 6 Gleitschuhen gebildet wird.
zurück weiterDie primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo10.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
----------------------------------------------------------------------
Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp
----------------------------------------------------------------------
-1- Reynoldssche Dgl. mit "Guembelscher Randbedingung" (Theo = 1)
-2- Belastung des Lagers vorgegeben (Last = 2)
-3- Vollstaendig umschlossenes Lager (Vollum = 1)
-4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1)
-5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1)
-6- Gerade Welle (Biege = 1)
-7- Keine versetzten Lagerabschnitte (Versatz = 1)
-8- Welle ideal zylindrisch (Welle = 1)
-9- Lagerschale nur mit starrer punktw. geg. Formabweich. (Schale = 3)
-20- Evtl. einige Eingabeparameter zeitabhaengig (Dynamic = 2)
-21- Zeitschritte DT konstant (SchrittVar = 1)
-22- Omega konstant (OmegaVar = 1)
-24- F1(T)=F1Amp*sin(Omega1*T-Phi1)+F1Mit (LastVar = 5)
F2(T)=F2Amp*sin(Omega2*T-Phi2)+F2Mit
-30- Auszer den Bezugsparametern alle anderen dimensionslos (Dim = 3)
Das Demonstrationsbeispiel entspricht im Wesentlichen dem Demonstrationsbeispiel "Demo09". Es wird hier allerdings eine instationäre Lagerbelastung angenommen. Der Betrag der Lagerbelastung ist weiterhin konstant, aber die Kraftrichtung läuft mit der Wellendrehung um. Das könnte z.B. bei einer Unwucht des rotierenden Bauteils der Fall sein.
Eingabe der Geometrie der Gleitschuhe siehe Demonstrationsbeispiel "Demo09" Abschnitt 4.8.9.
Nachfolgende Bilder zeigen einige Darstellungsmöglichkeiten der Ergebnisse.
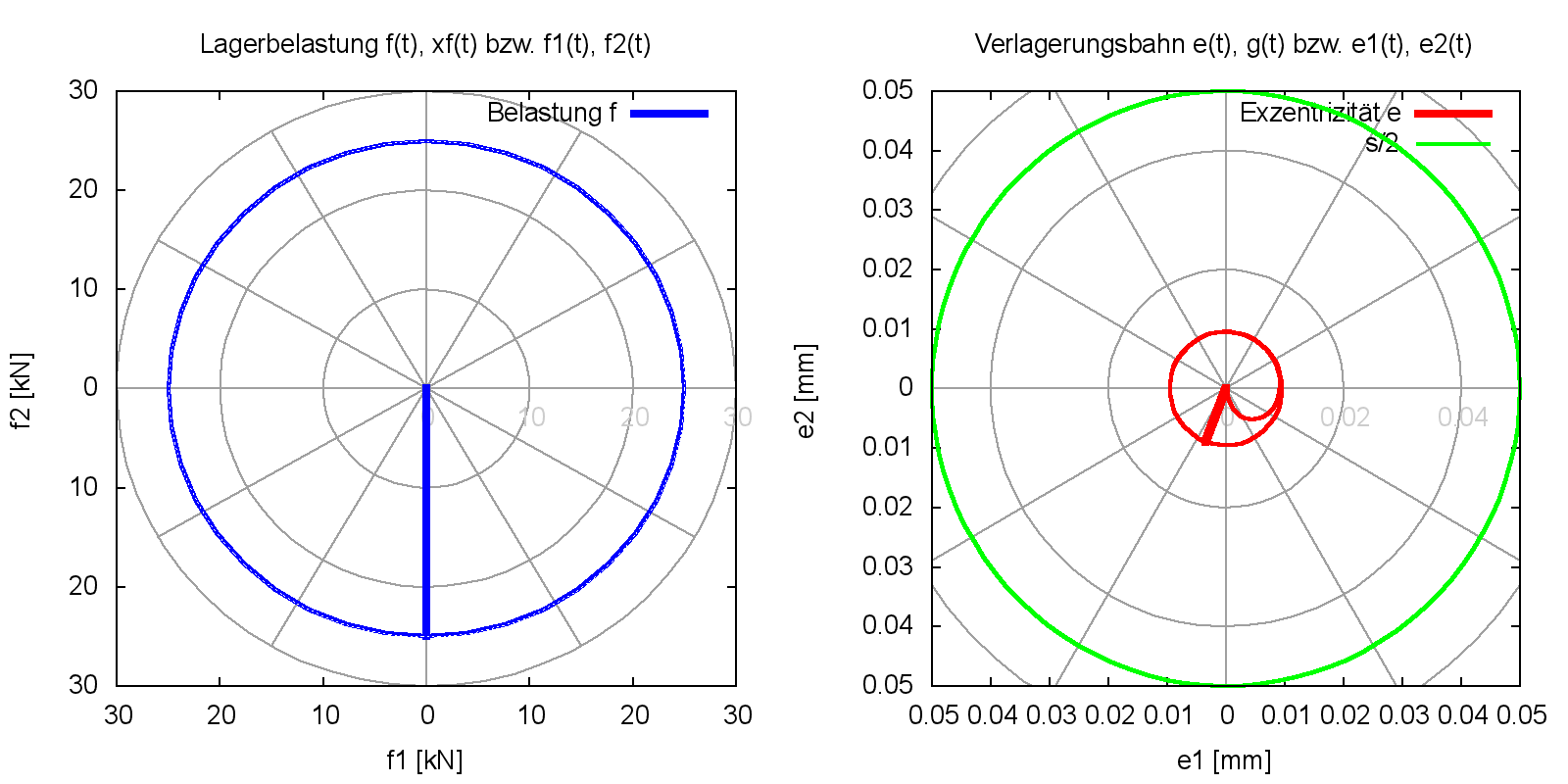
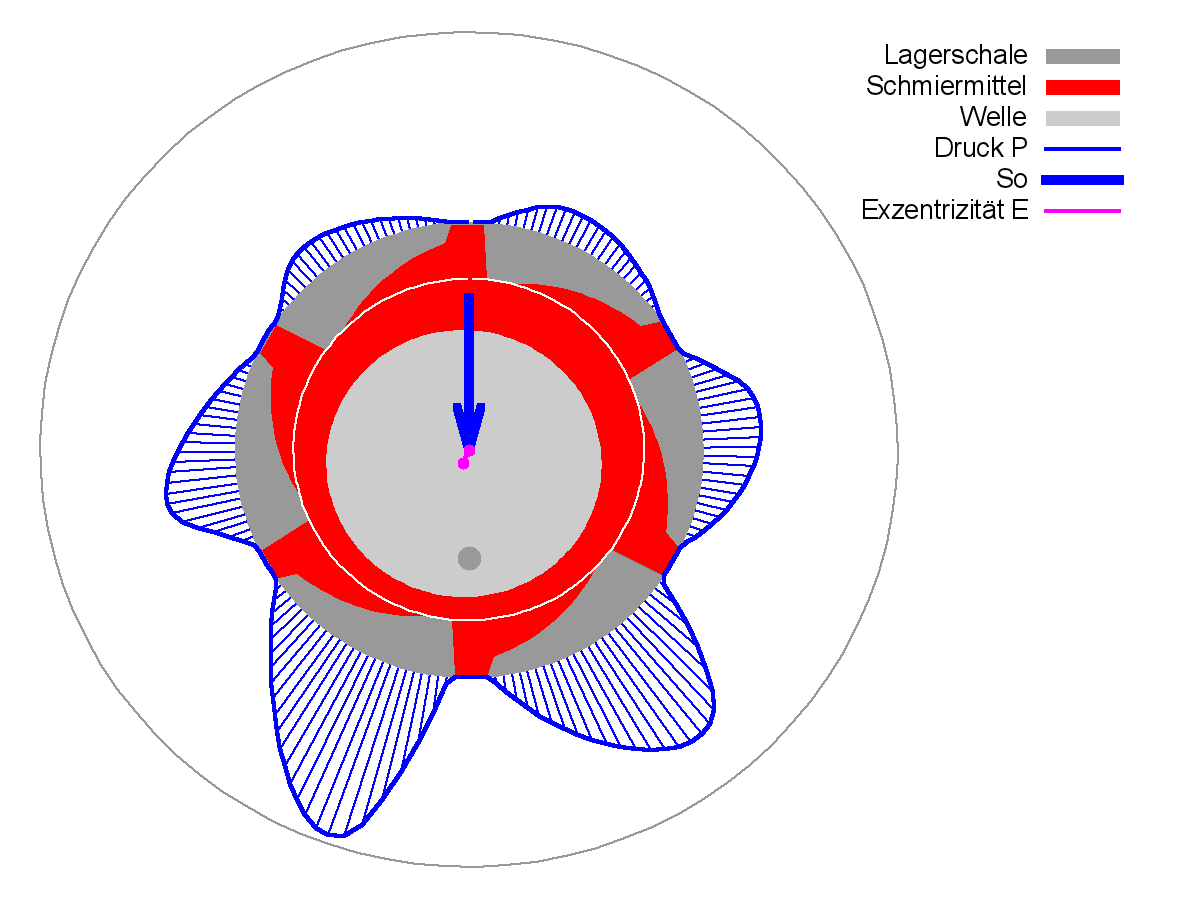
Bild 4.092: Verlagerungsbahn über zwei Wellenumdrehung, einschließlich Anlaufphase (Bilddatei: Demo10-Dim-2d-Pol-f-e-JT=81.png) (Animation: Demo10-Dim-2d-Pol-f-e.wmv)
Bild 4.092 zeigt links den Verlauf der umlaufenden Lagerbelastung über 2 Umdrehungen und rechts die zugehörige Verlagerungsbahn. Die 1.Umdrehung stellt die Einlaufphase der Berechnung dar, beginnend bei einer konzentrischen Anfangslage der Welle. Mit der 2.Umdrehung hat das Lager bereits seine geschlossene zyklische Verlagerungsbahn erreicht. Der dicke blaue Balken und der dicke rote Balken in den Diagrammen stellen jeweils die Größe und die Richtung der Lagerbelastung f bzw. der Wellenverlagerung e zum letzten berechneten Zeitpunkt JT=81 dar.
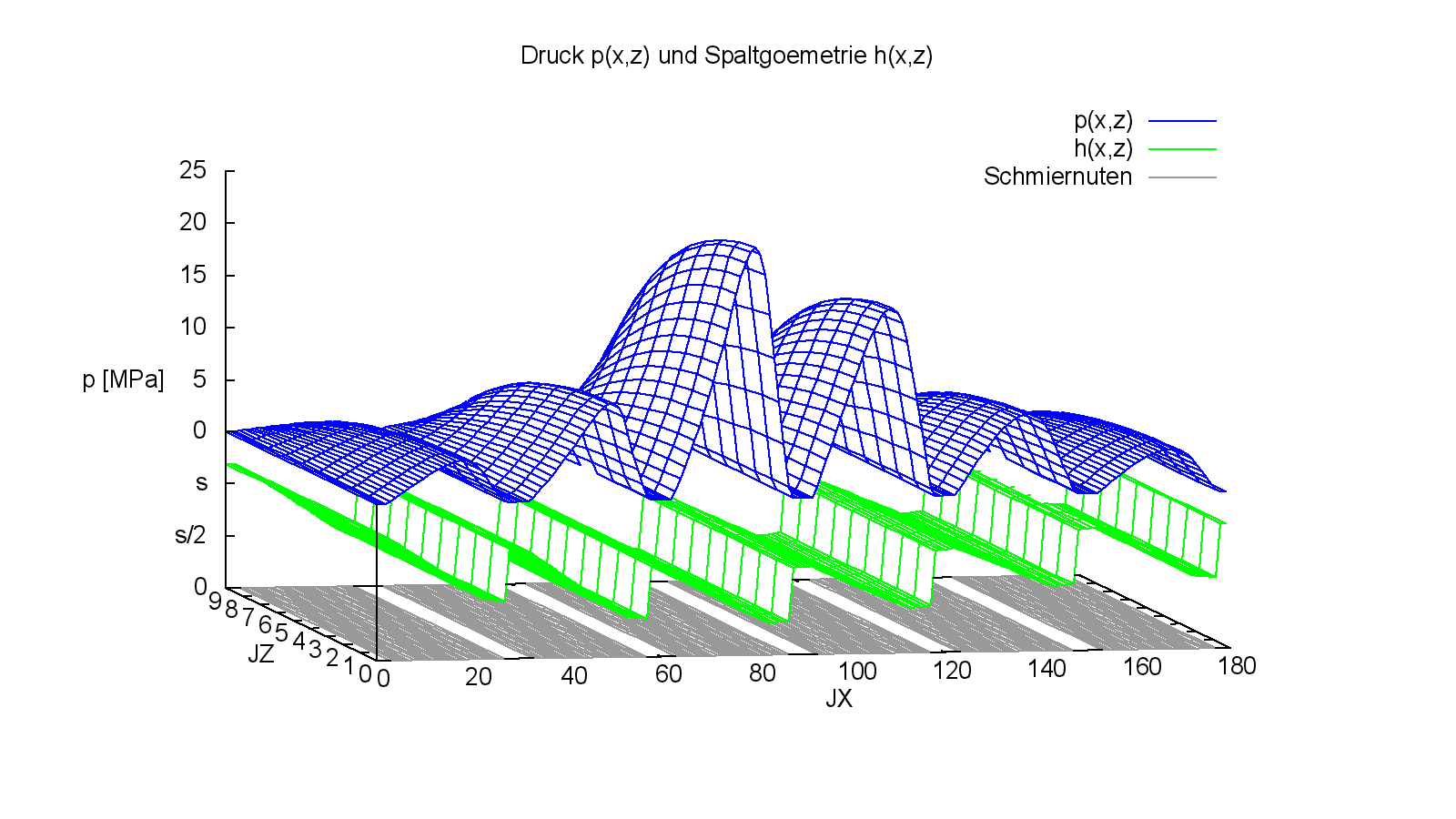
Bild 4.093: Druckverteilung p und Spaltgeometrie h zum letzten Zeitpunkt JT=81 des Demonstrationsbeispiels Demo10 (Bilddatei: Demo10-Dim-3d-Abw-p-h-Nut-JT=81.png) (Animation: Demo10-Dim-3d-Abw-p-h-Nut.wmv)
Die 3-d-Darstellung der Spalthöhe h(x,z) in Bild 4.093 ist nicht besonders anschaulich, weil hier der Eindruck entstehen könnte, dass die Keilschuhe an der Wellenoberfläche angeordnet sind, was prinzipiell auch möglich wäre. Anschaulicher ist hier die 2-d-Darstelung in Bild 4.094.
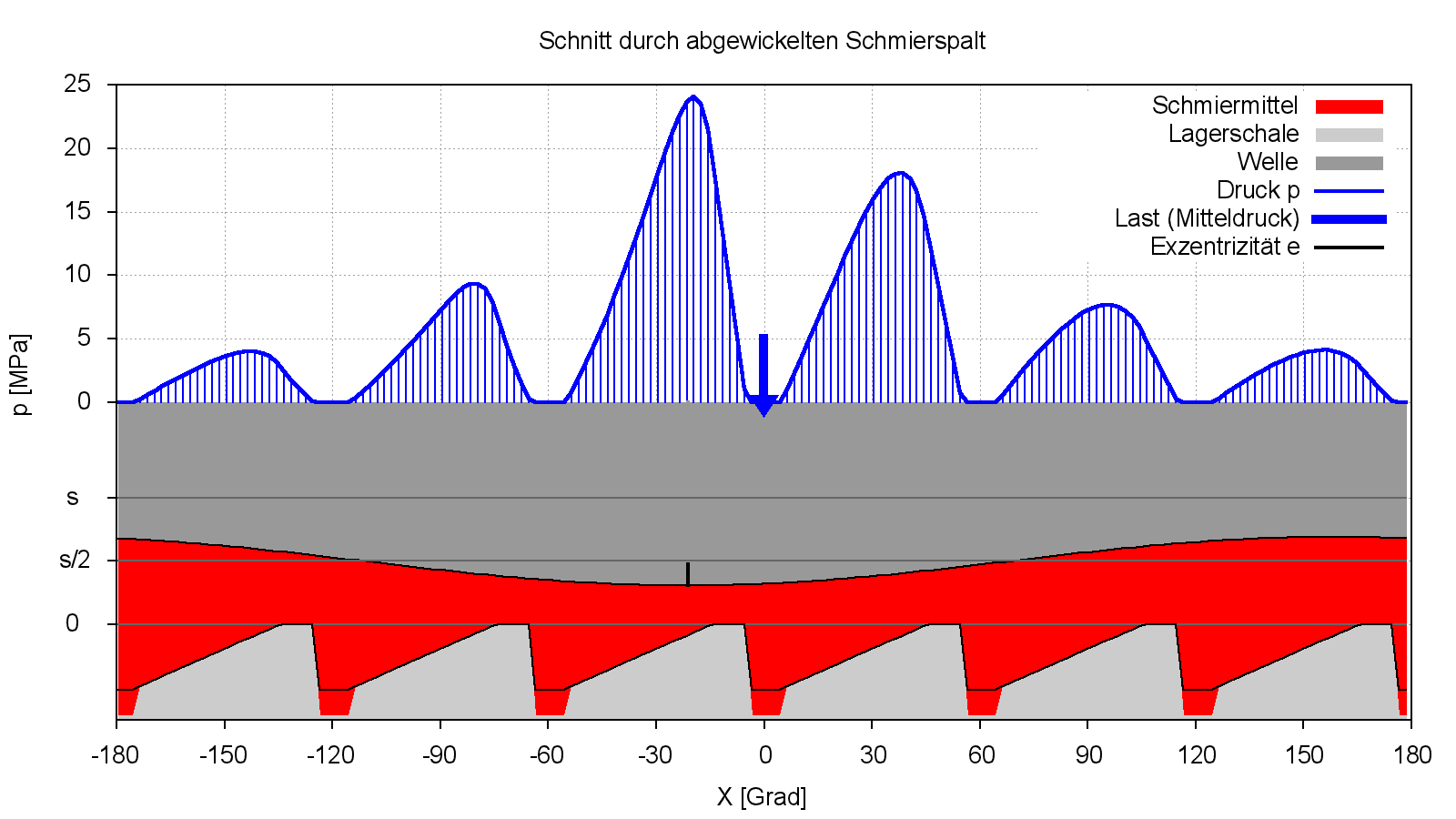
Bild 4.094: Druckverteilung p und Spaltgeometrie h in Lagermitte zum letzten Zeitpunkt JT=81 des Demonstrationsbeispiels Demo10 (Bilddatei: Demo10-Dim-2d-Abw-p-h-JT=81-JZ=1.png) (Animation: Demo10-Dim-2d-Abw-p-h-JZ=1.wmv)
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo11.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2) -2- Belastung des Lagers vorgegeben (Last = 2) -3- Teilweise umschlossenes Lager (Vollum = 2) -4- Asymmetrisches Lager (Sym = 2) -5- Verkantete Welle innerhalb der Lagerschale (Kante = 2) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle ideal zylindrisch (Welle = 1) -9- Lagerschale nur mit Formabweichungsfunktionen (Schale = 2) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Auszer den Bezugsparametern alle anderen dimensionslos (Dim = 3)
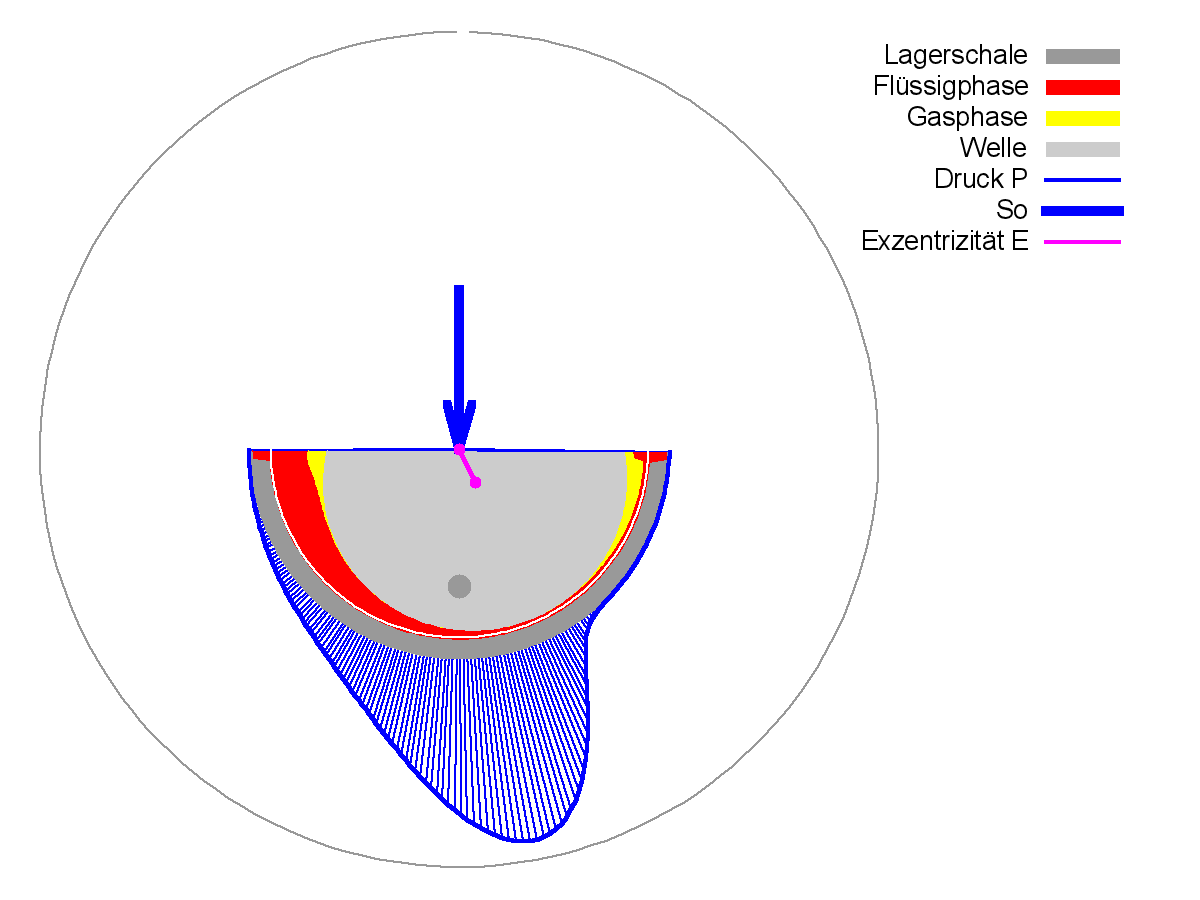
Demonstrationsbeispiel "Demo11" zeigt einige Varianten der Lager- bzw. Spaltgeometrie. Diese werden gut anschaulich gemacht durch die Darstellung des Spielraums des Lagers (Bild 4.096).

Bild 4.096: Spielraum des Lagers zum Demonstrationsbeispiel Demo11 (Bilddatei: Demo11-Dim-3d-Zyl-spiel-JT=21.png)
Die Lagerschale ist leicht ballig und außerdem noch konisch in die gleiche Richtung wie die Welleverkantung. Dadurch wird zum Teil die Kantenpressung gemildert.
Bild 4.097 und 4.098 zeigen die Druckverteilung p, die Spalthöhe h und die Flüssigkeitsverteilung hF über die abgewickelte Schaltfläche im stationären Zustand.
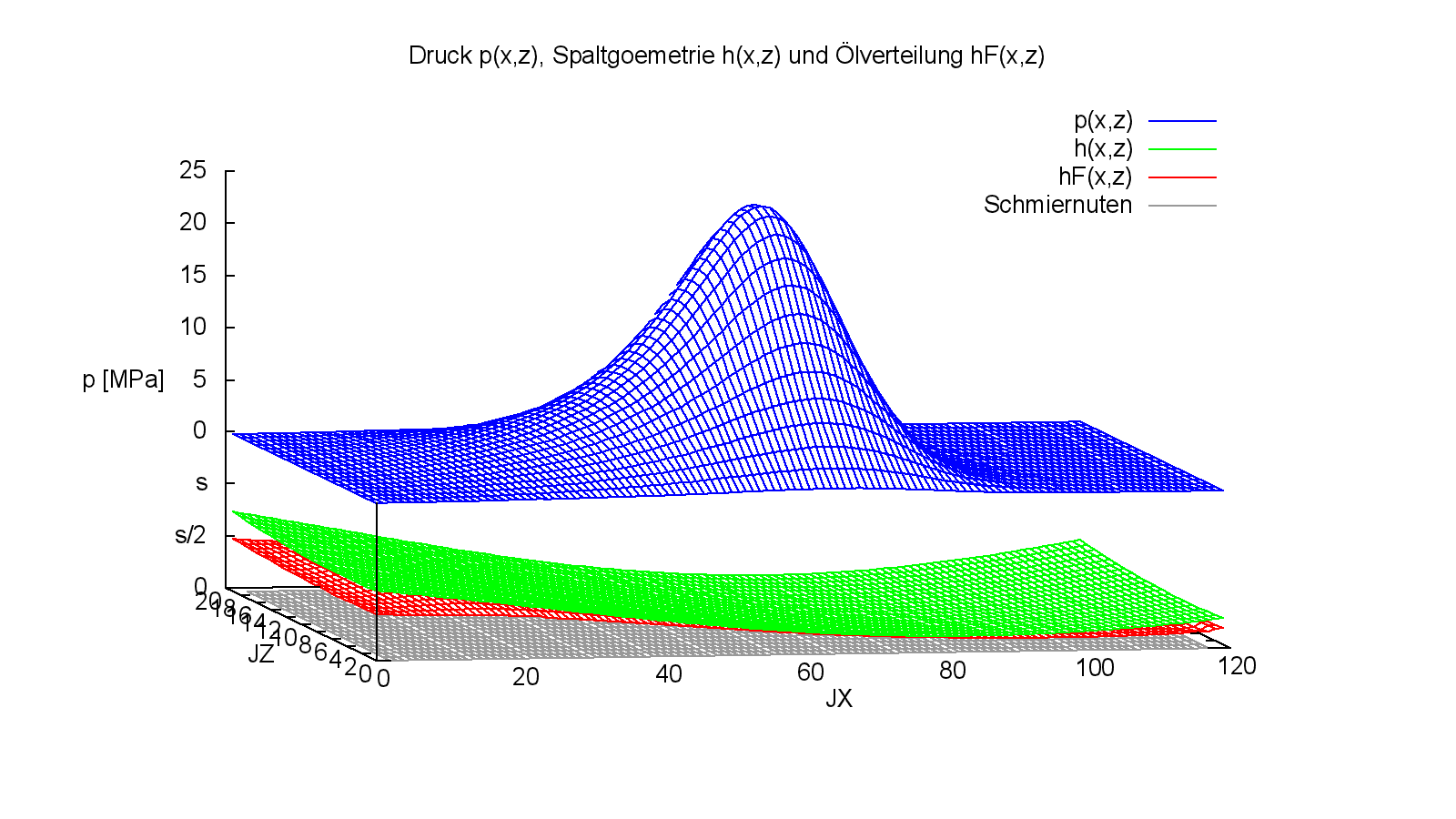
Bild 4.097: Druckverteilung p, Spaltgeometrie h und Schmierflüssigkeitsverteilung hF im stationären Zustand des Demonstrationsbeispiels Demo11 (Bilddatei: Demo11-Dim-3d-Abw-p-h-hF-Nut-JT=21.png)
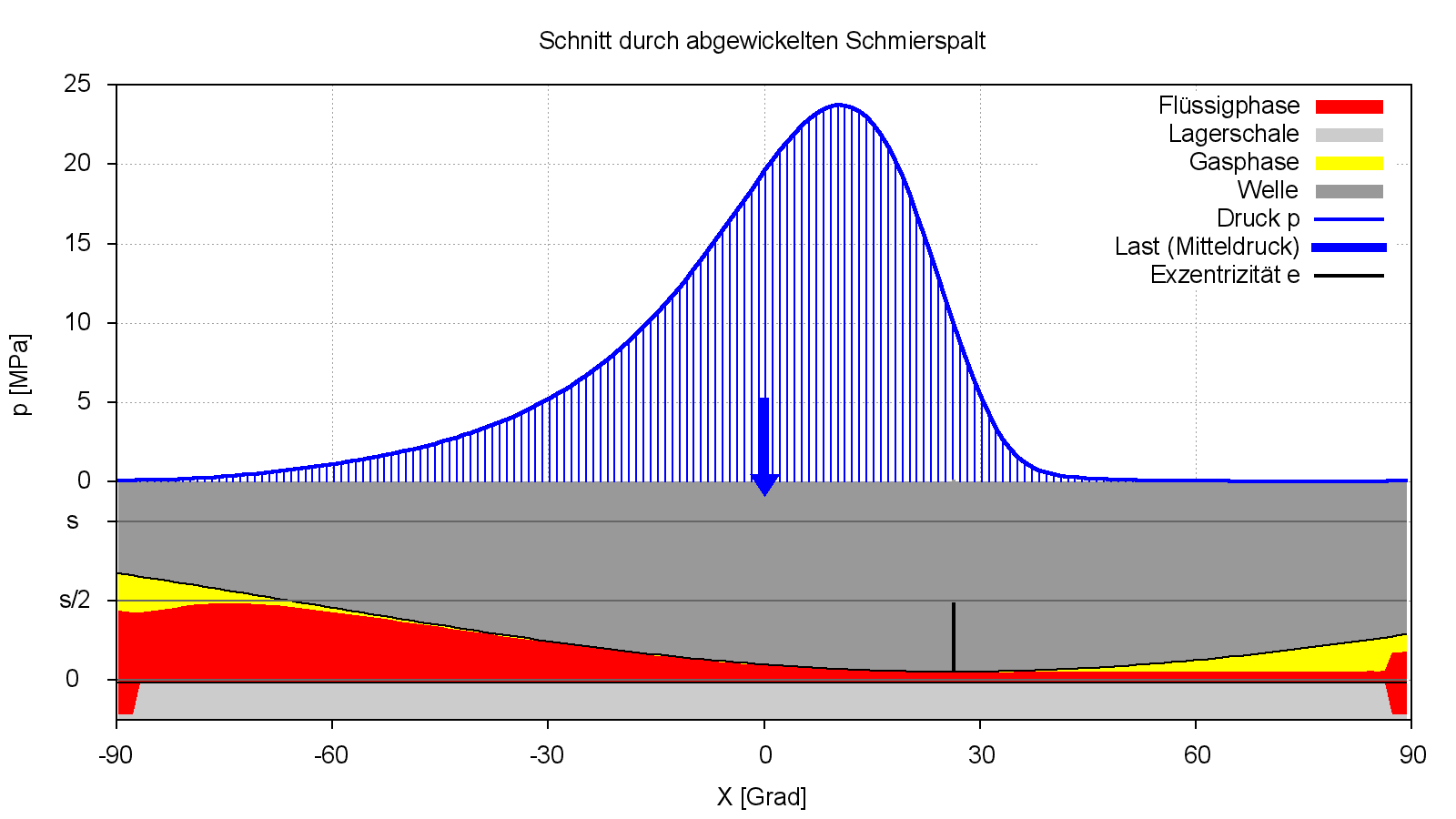
Bild 4.098: Druckverteilung p, Spaltgeometrie h und Schmierflüssigkeitsverteilung hF im stationären Zustand des Demonstrationsbeispiels Demo11 (Bilddatei: Demo11-Dim-2d-Abw-p-h-hF-JT=21-JZ=13.png)
Im Bild 4.098 wird der Querschnitt durch die Schnittebene JZ=13 dargestellt. Das ist nicht die Lagermitte, sondern der Querschnitt in dem das Druckmaximum liegt.
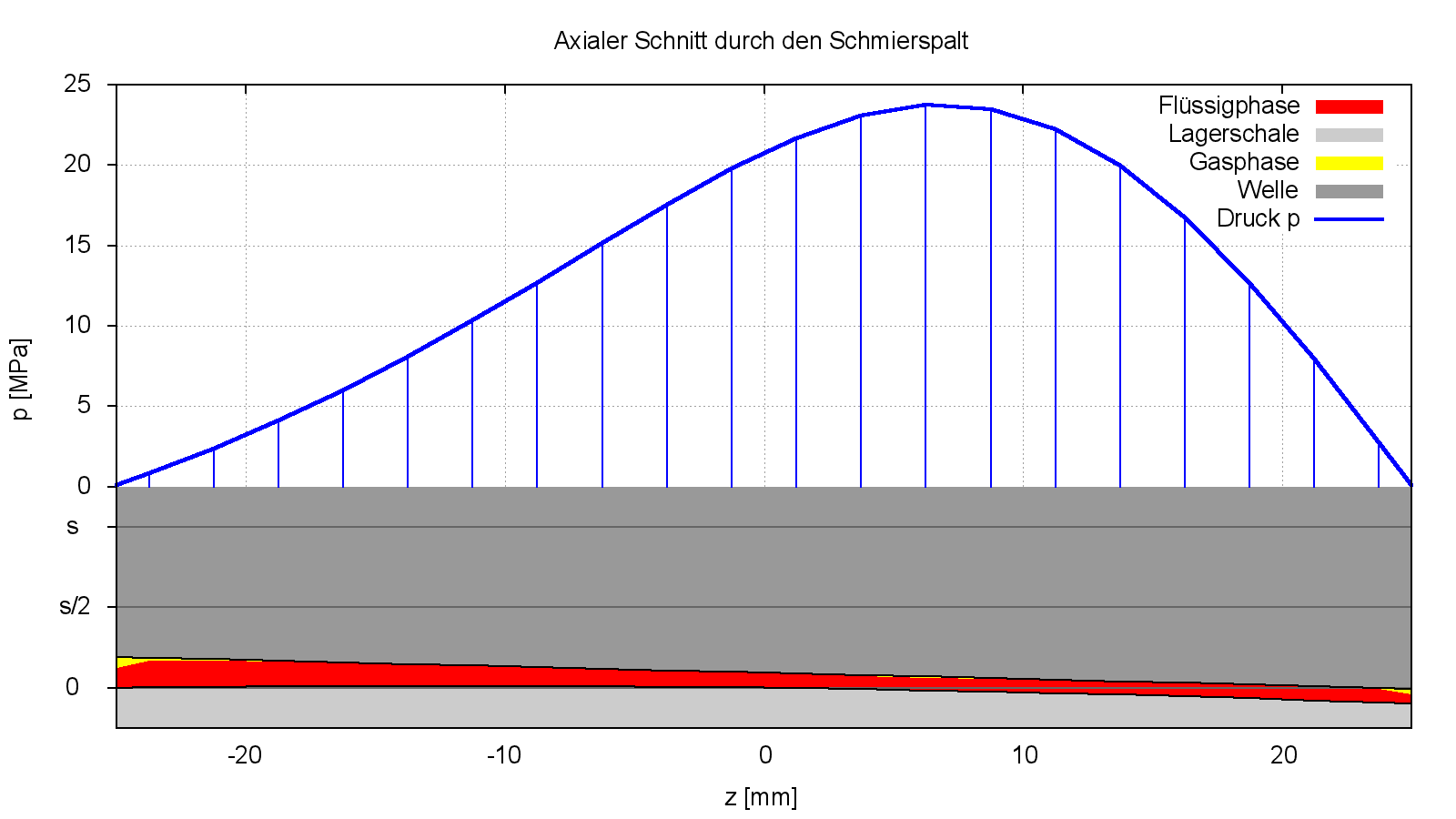
Bild 4.099 zeigt nun noch einen Axialschnitt durch das Lager. Auch hier wird die Schnittebene JX=202 ausgewählt, in der das Druckmaximum liegt.
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo12.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:

Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
----------------------------------------------------------------------
Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp
----------------------------------------------------------------------
-1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2)
-2- Belastung des Lagers vorgegeben (Last = 2)
-3- Teilweise umschlossenes Lager (Vollum = 2)
-4- Asymmetrisches Lager (Sym = 2)
-5- Verkantete Welle innerhalb der Lagerschale (Kante = 2)
-6- Gerade Welle (Biege = 1)
-7- Keine versetzten Lagerabschnitte (Versatz = 1)
-8- Welle ideal zylindrisch (Welle = 1)
-9- Lagerschale nur mit Formabweichungsfunktionen (Schale = 2)
-20- Evtl. einige Eingabeparameter zeitabhaengig (Dynamic = 2)
-21- Zeitschritte DT konstant (SchrittVar = 1)
-22- Omega konstant (OmegaVar = 1)
-24- F1(T)=F1Amp*sin(Omega1*T-Phi1)+F1Mit (LastVar = 5)
F2(T)=F2Amp*sin(Omega2*T-Phi2)+F2Mit
-25- Kant1(T)=Kant1Amp*sin(Omega1Kant*T-Phi1Kant)+Kant1Mit(KantVar= 5)
Kant2(T)=Kant2Amp*sin(Omega2Kant*T-Phi2Kant)+Kant2Mit
-30- Auszer den Bezugsparametern alle anderen dimensionslos (Dim = 3)
Das Demonstrationsbeispiel "Demo12" ist identisch mit dem Demonstrationsbeispiel "Demo11", außer dass hier eine schwellende Lagerbelastung vorgegeben ist. Bild 4.101 zeigt links den vorgegebenen Verlauf der Lagerbelastung und rechts die berechnete Verlagerungsbahn über 2 Wellenumdrehungen und gleichzeitig 2 Lastzyklen. Während der 1.Umdrehung erfolgt die Anlaufrechnung. Während der 2.Umdrehung ist die geschlossene zyklische Verlagerungsbahn bereits erreicht. Die zum statischen Bild gehörende Animation zeigt nur den Lastverlauf und die Verlagerungsbahn über die 2.Wellenumdrehung.
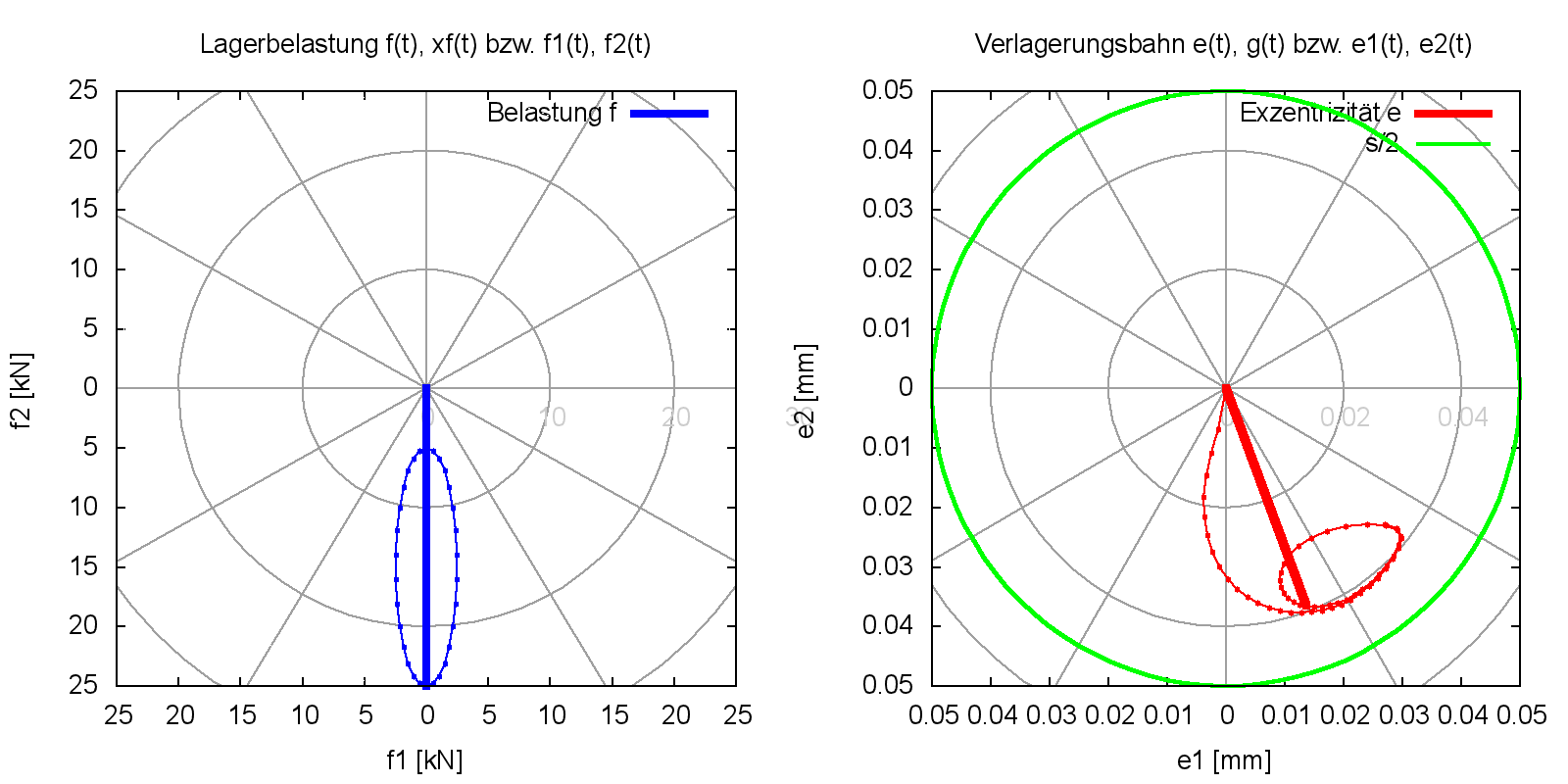
Bild 4.101: Verlagerungsbahn über zwei Wellenumdrehung, einschließlich Anlaufphase (Bilddatei: Demo12-Dim-2d-Pol-f-e-Punkte-JT=46.png) (Animation: Demo12-Dim-2d-Pol-f-e-Punkte.wmv)
Auch die Verkantung wird hier zeitlich veränderlich angenommen. Sie hat einen synchron zur Lagerbelastung schwellenden Verlauf. Die Bewegung der Wellenachse einschließlich Verkantung wird gut anschaulich gemacht durch die Darstellung im Spielraum des Lagers (Bild 4.102).
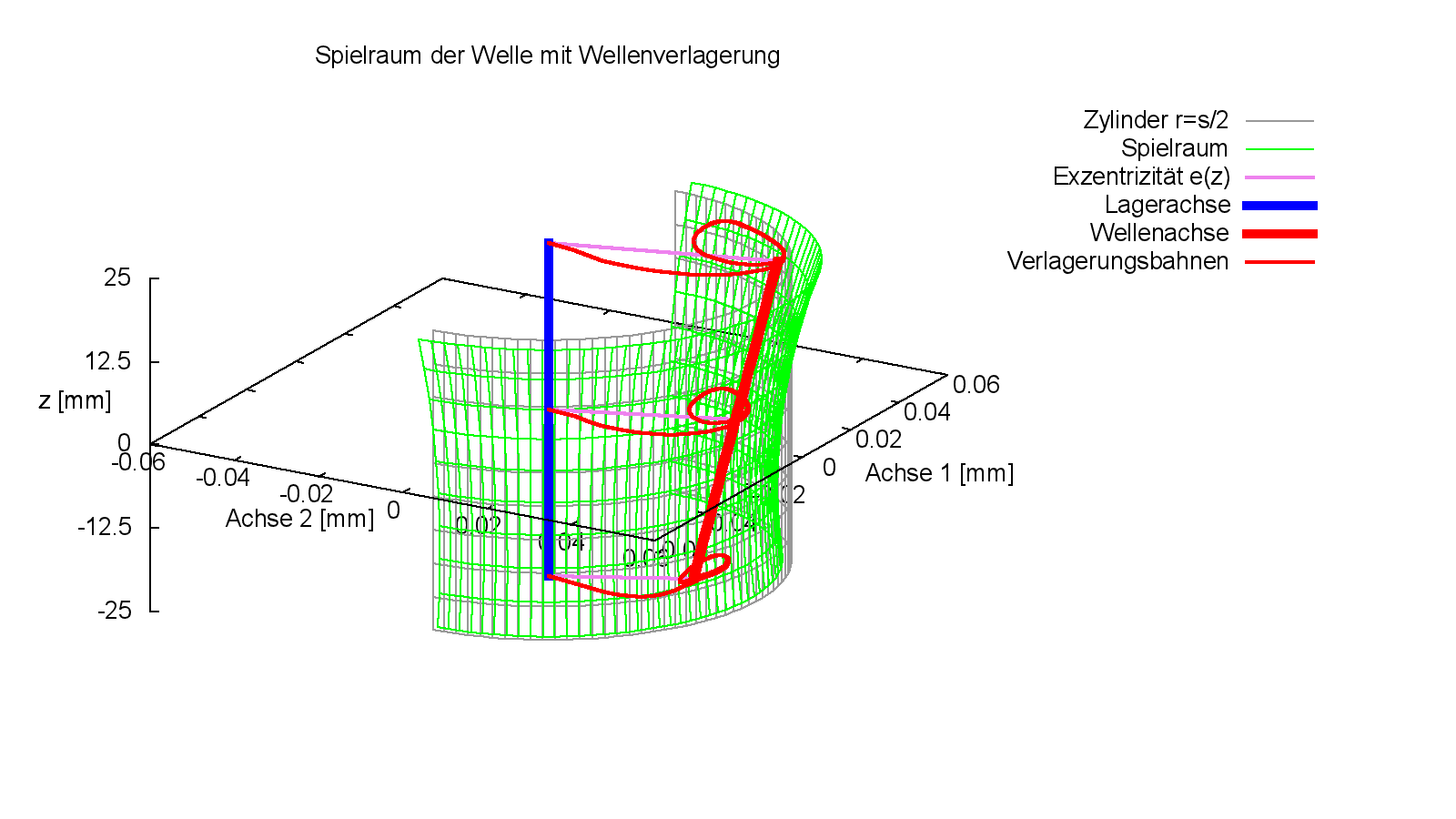
Bild 4.102: Spielraum des Lagers zum Demonstrationsbeispiel Demo12 (Bilddatei: Demo12-Dim-3d-Zyl-spiel-JT=46.png) (Animation: Demo12-Dim-3d-Zyl-spiel.wmv)
Das statische Bild zeigt die Verlagerung der Wellenachse (rot) zum Zeitpunkt JT=46 der maximalen Lagerbelastung. An den Enden der Wellenachse und in der Lagermitte sind die örtlichen Verlagerungsbahnen dargestellt, einschließlich während der Anlaufrechnung der 1. Wellenumdrehung.
Die zugehörige Animation zeigt nur die 2.Wellenumdrehung mit den bereits zyklisch geschlossenen Verlagerungsbahnen der Wellenachse.
Bild 4.103 und 4.104 zeigen die Druckverteilung p, die Spalthöhe h und die Flüssigkeitsverteilung hF über die abgewickelte Schaltfläche zum Zeitpunkt JT=46 der maximalen Lagerbelastung. Die zugehörigen Animationen zeigen den zeitlichen Verlauf während der 2. Wellenumdrehung JT=31 bis 61.
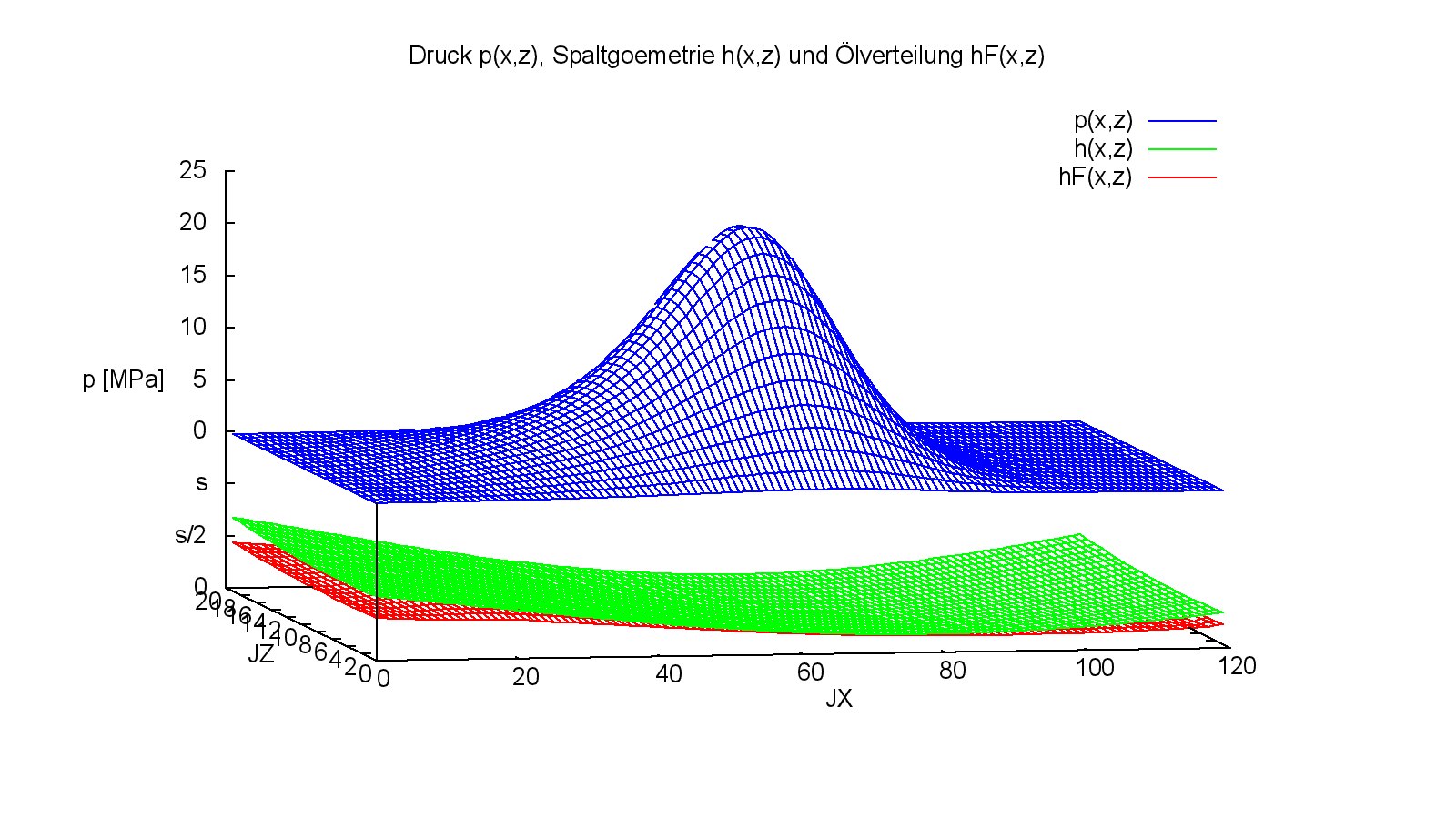
Bild 4.103: Druckverteilung p, Spaltgeometrie h und Schmierflüssigkeitsverteilung hF zum Zeitpunkt JT=46 des Demonstrationsbeispiels Demo12 (Bilddatei: Demo12-Dim-3d-Abw-p-h-hF-JT=46.png) (Animation: Demo12-Dim-3d-Abw-p-h-hF.wmv)
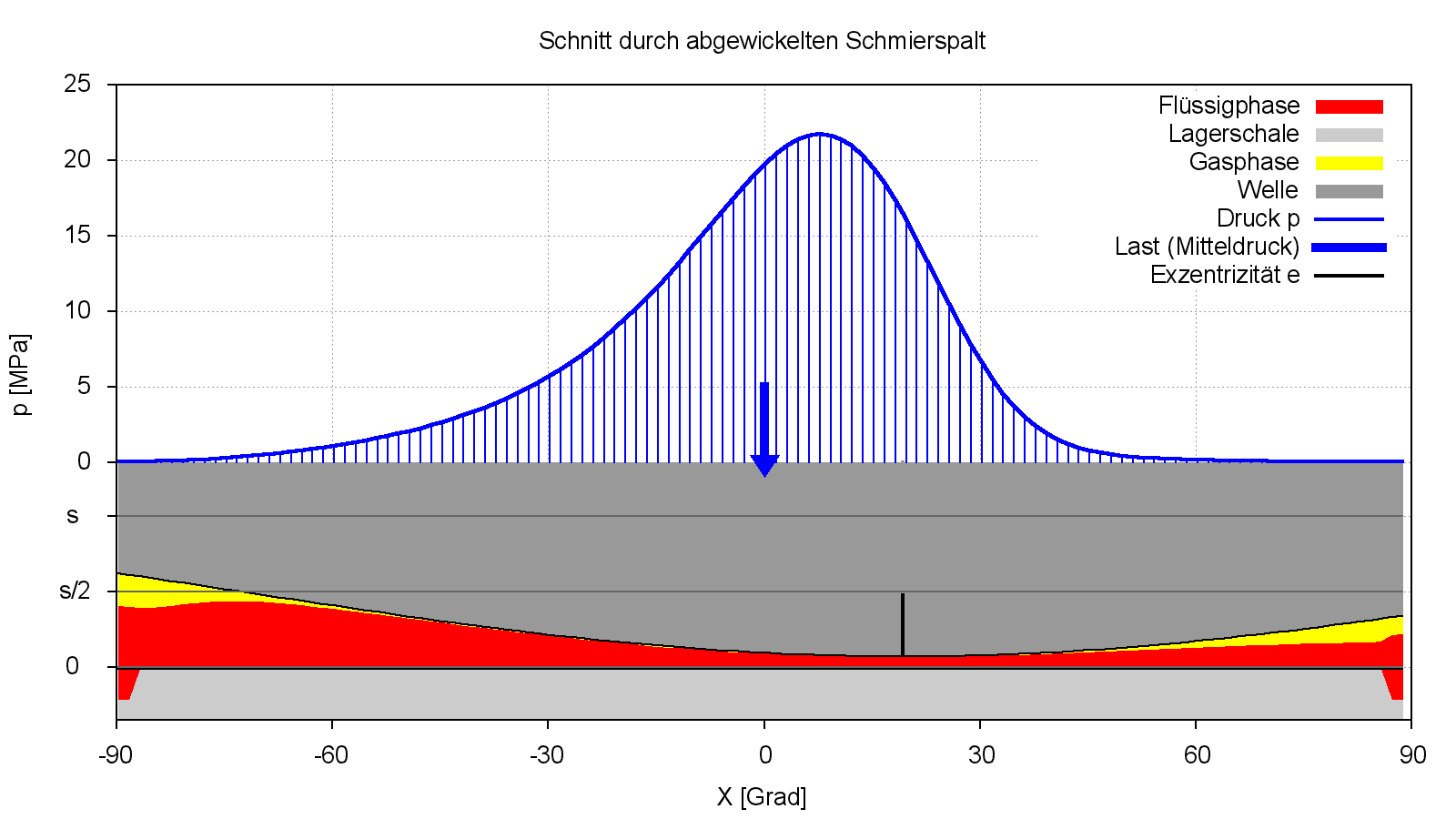
Im Bild 4.104 wird der Querschnitt durch die Schnittebene JZ=13 dargestellt. Das ist nicht die Lagermitte, sondern der Querschnitt, in dem das Druckmaximum während der maximalen Lagerbelastung liegt.
zurück weiterDie primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo13.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
---------------------------------------------------------------------- Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp ---------------------------------------------------------------------- -1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2) -2- Belastung des Lagers vorgegeben (Last = 2) -3- Vollstaendig umschlossenes Lager (Vollum = 1) -4- Symmetrisches Lager (Sym.-ebene senkrecht zu Rot.-achse) (Sym = 1) -5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1) -6- Gerade Welle (Biege = 1) -7- Keine versetzten Lagerabschnitte (Versatz = 1) -8- Welle mit Formabweichungensfunktion (Welle = 2) -9- Lagerschale nur mit Formabweichungsfunktionen (Schale = 2) -20- Alle Eingabeparameter zeitlich konstant (Dynamic = 1) -30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
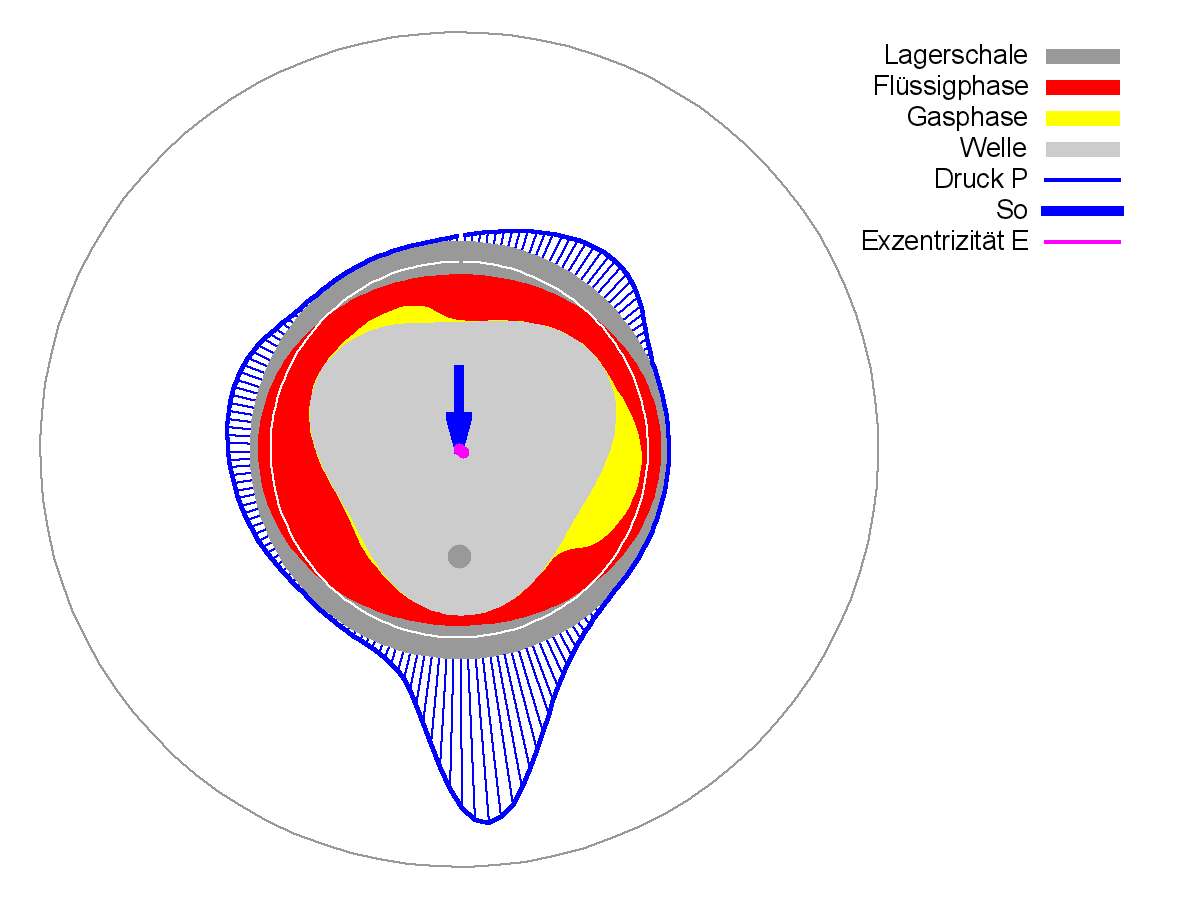
Dieses Demonstrationsbeispiel hat eine Besonderheit: Es sind alle Eingabebedingungen zeitlich konstant (Dymanic=1) und trotzdem sind die Ergebnisdaten auch nach der Einlaufphase über die Zeit variabel. Die Ursache liegt in der Unrundheit der Welle. So bewegt sich die Wellenachse auf einer zyklischen Verlagerungsbahn, obwohl die Lagerbelastung zeitlich konstant ist. Bild 4.106 zeigt diese Verlagerungsbahn für eine Wellenumdrehung. Das erste Drittel der Wellendrehung zeigt die Einlaufphase und die restlichen 2/3 durchläuft der Wellenmittelpunkt bereits die zyklische Wellenverlagerungsbahn. Da die Welle "dreieckig" ist, wird die zyklische Verlagerungsbahn pro Wellenumdrehung dreimal durchlaufen.
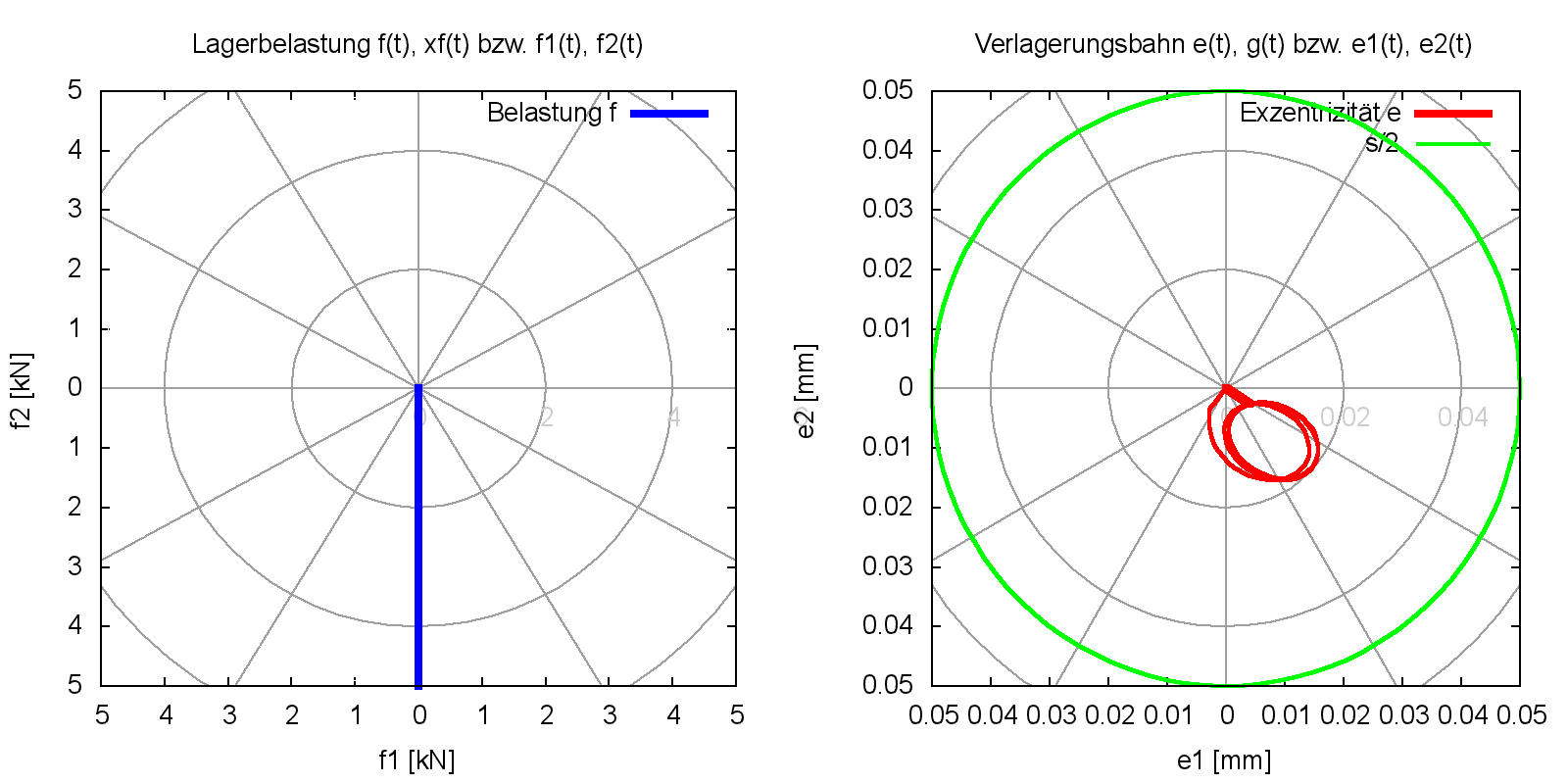
Bild 4.106: Verlagerungsbahn über eine Wellenumdrehung einschließlich Anlaufphase für ein Lager mit unrunder Welle und unrunder Lagerschale (Bilddatei: Demo13-Dim-2d-Pol-f-e-JT=361.png)
In der axialen Ansicht auf den Spielraum des Lagers (Bild 4.107) kann man dessen Verformung gegenüber dem zylindrischen Spielraum eines Lagers mit ideal runder Welle und Lagerschale sehen. In der zugehörigen Animation sieht man dann auch seine zeitlichen Veränderungen. In der Animation wird nur der zyklische Verlauf der Verlagerungen der Welle gezeigt, ohne Anlaufphase.
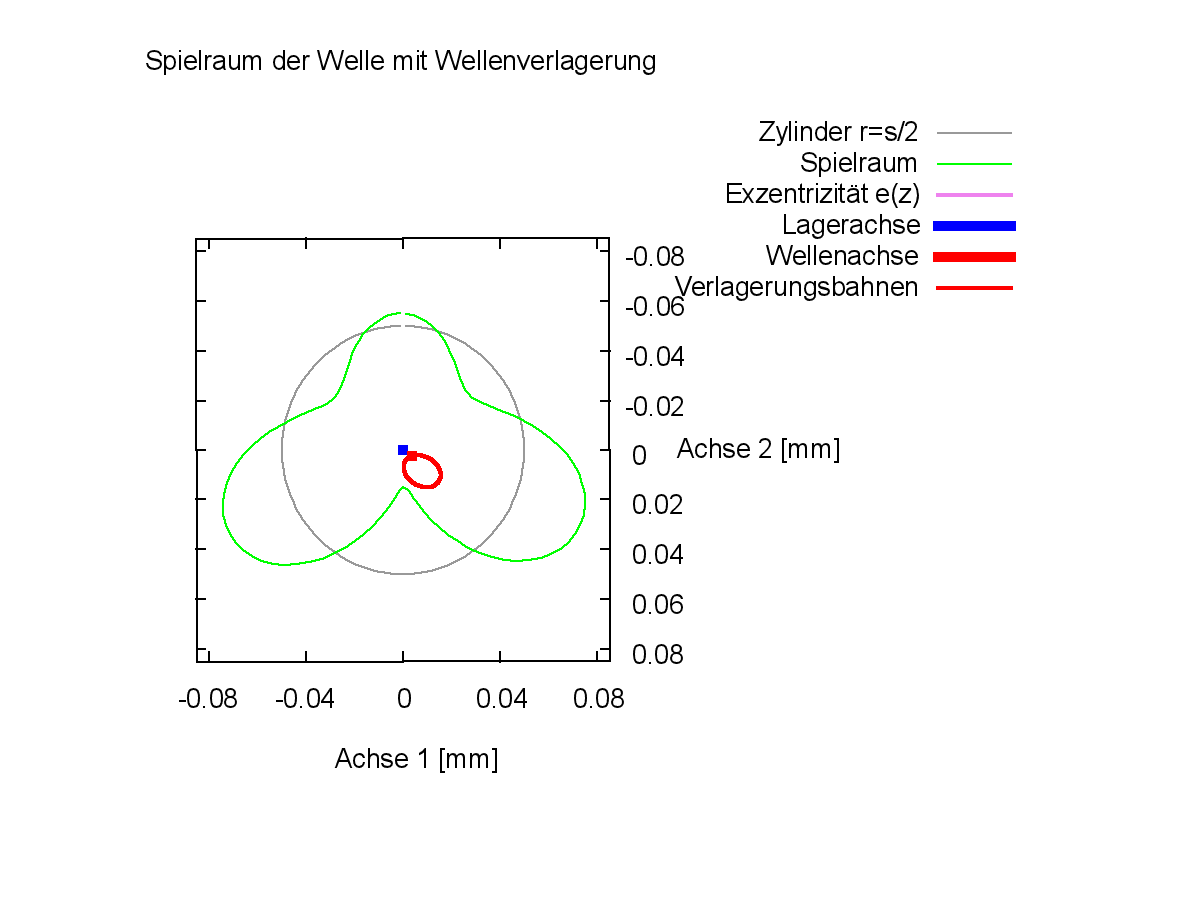
Bild 4.107: Axiale Ansicht des Spielraums eines Lagers mit elliptischer Lagerschale und "dreieckiger" Welle (Bilddatei: Demo13-Dim-3d-Zyl-spiel-JT=361.png) (Animation: Demo13-Dim-3d-Zyl-spiel.wmv)
Bild 4.108 zeigt nun noch die Druckverteilung, die Spaltgeometrie und die Verteilung der Schmierflüssigkeit über den Lagerumfang in Lagermitte zum Zeitpunkt JT=361 und die zugehörige Animation zeigt diese Verteilung in ihrem zyklischen Verlauf.
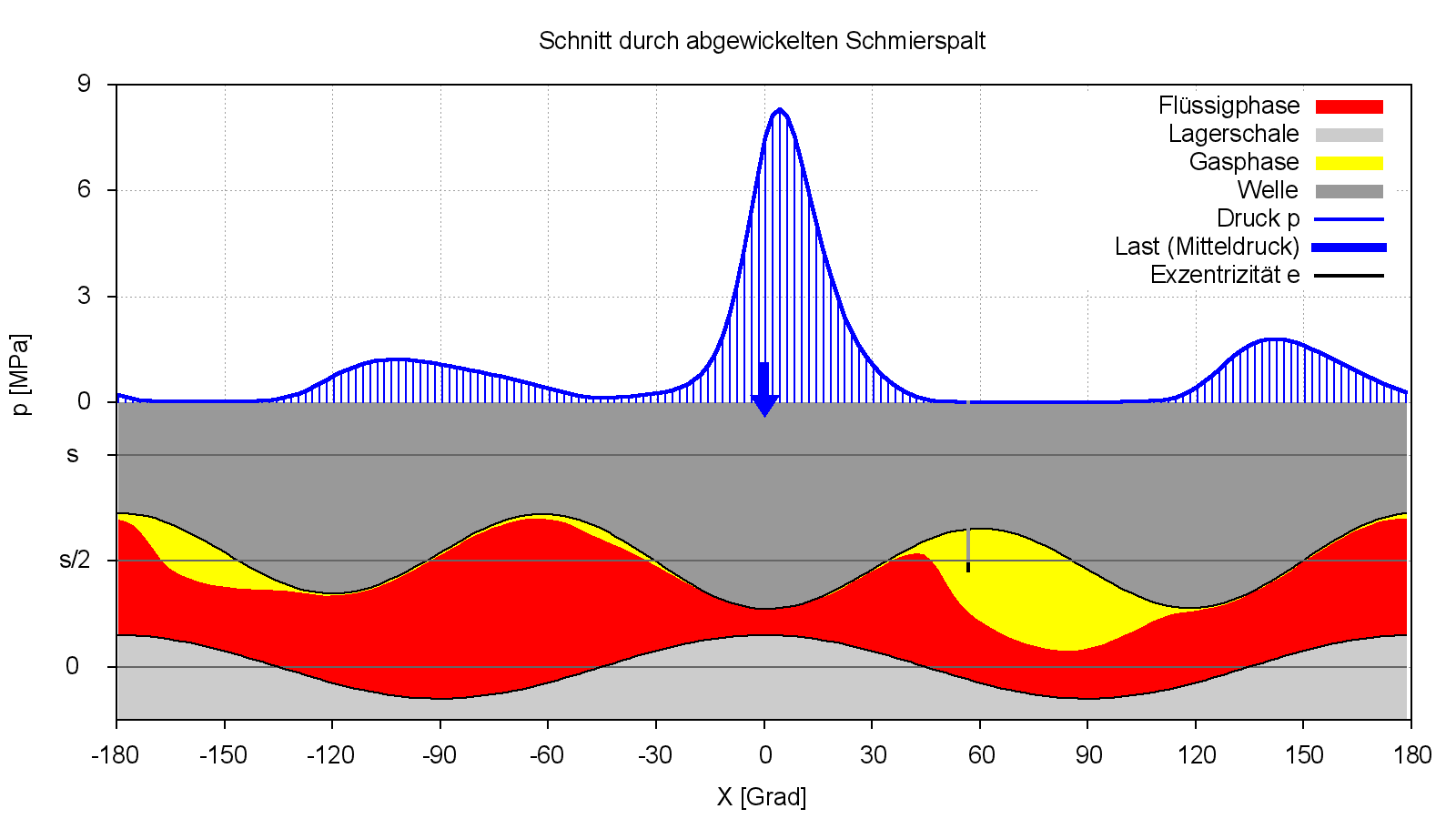
Bild 4.108: Druckverlauf, Spaltgeometrie und Schmierflüssigkeitsverteilung in Lagermitte zum letzten berechneten Zeitpunkt JT=361 in einem Lager mit elliptischer Lagerschale und "dreieckiger" Welle (Bilddatei: Demo13-Dim-2d-Abw-p-h-hF-JT=361-JZ=1.png) (Animation: Demo13-Dim-2d-Abw-p-h-hF-JZ=1.wmv)
Die kompletten primären Eingabe- und Ergebnisdaten zu dem Demonstrationsbeispiel einschließlich Anlaufrechnung sind in der Datei "Demo13.txt" im Verzeichnis "./DatenDemo" abgelegt. Sie hat eine Größe von 16 MB. Um das eigentlich interessierende Ergebnis, von einem Durchlauf der zyklischen Verlagerungsbahn abzuspeichern, was hier 1/3 Wellenumdrehung entspricht, können 2/3 Speichervolumen gespart werden. Die Datei Demo13-1.txt enthält die Eingabe- und Ergebnisdaten des eigentlich interessierenden Ergebnisses und hat ein Volumen von 5,5 MB. Zur Verfahrensweise siehe Erläuterungen zu Demonstrationsbeispiel Demo01, Abschnitt 4.8.1.
zurück weiterDie primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo14.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:

Die Angaben im 2.Hauptmenü beschreiben die qualitativen Merkmale des Lagerbeispiels:
----------------------------------------------------------------------
Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp
----------------------------------------------------------------------
-1- Erweiterte Reynoldssche Differentialgleichung (Theo = 2)
-2- Belastung des Lagers vorgegeben (Last = 2)
-3- Teilweise umschlossenes Lager (Vollum = 2)
-4- Asymmetrisches Lager (Sym = 2)
-5- Fluchtende Welle bezogen auf Lagerschale (Kante = 1)
-6- Gerade Welle (Biege = 1)
-7- Zwei versetzte Lagerabschnitte (Versatz = 2)
-8- Welle ohne weitere Formabweichungen (Welle = 1)
-9- Lagerschale ohne weiteren Formabweichungen (Schale = 1)
-20- Evtl. einige Eingabeparameter zeitabhaengig (Dynamic = 2)
-21- Zeitschritte DT konstant (SchrittVar = 1)
-22- XWe(T)=XWeAmp*sin(OmegaWe*T-PhiWe)+XWeMit (OmegaVar = 4)
-24- f1(T)=f1Amp*sin(Omega1*T-Phi1)+f1Mit (LastVar = 5)
f2(T)=f2Amp*sin(Omega2*T-Phi2)+f2Mit
-30- Dimensionsbehaftete Ein- und Ausgabeparameter (Dim = 2)
Die Definition des Lagerversatzes, der zugehörigen beschreibenden Parameter und Gleichungen findest Du im Abschnitt 2.1.2.16 bzw. 2.2.2.16. Die Beschreibung der Eingabe der Parameter findest Du in Abschnitt 4.4.4.11. Die Beschreibung der Eingabe der pendelnden Drehbewegung findest Du im Abschnitt 4.4.4.4.4.
Die Lagervariante "Lagerversatz" ist ein Sonderfall. Sie beruht auf einer Idee, die Tragfähigkeit für hydrodynamisch geschmierte Lager mit geringer Drehbewegung durch eine spezielle Spaltgeometrie zu erhöhen. Obwohl dem Autor bisher keine Anwendung dieser Idee bekannt geworden ist, wurde sie in das Programm aufgenommen, um mit dieser Variante zu demonstrieren, wie Sondervarianten in das erweiterungsfähige Baukastensystem des Programms eingefügt werden können und um die Leistungsfähigkeit der Berechnungsmethode zu testen. Ausführlicher wurde darüber bereits in der Veröffentlichung [21] berichtet. Das hier gezeigte Demonstrationsbeispiel entspricht der optimalen Auslegung der Veröffentlichung [21, Abschnitt 5]. Es wurden je 2 Schmiertaschen mitten in die Bereiche des tragenden Schmierspalts angeordnet. Die Zuleitungen zu den Taschen sind mit Rückschlagventilen ausgerüstet, so dass Schmiermittel einströmen, aber nicht wieder abfließen kann.
Die Berechnung hat nach einer Anlaufrechnung von einem Zyklus der Pendelbewegung über 200 Zeitschritte eine zyklische Verlagerungsbahn erreicht. Bild 4.110 zeigt die berechnete Verlagerungsbahn ohne Anlaufrechnung.
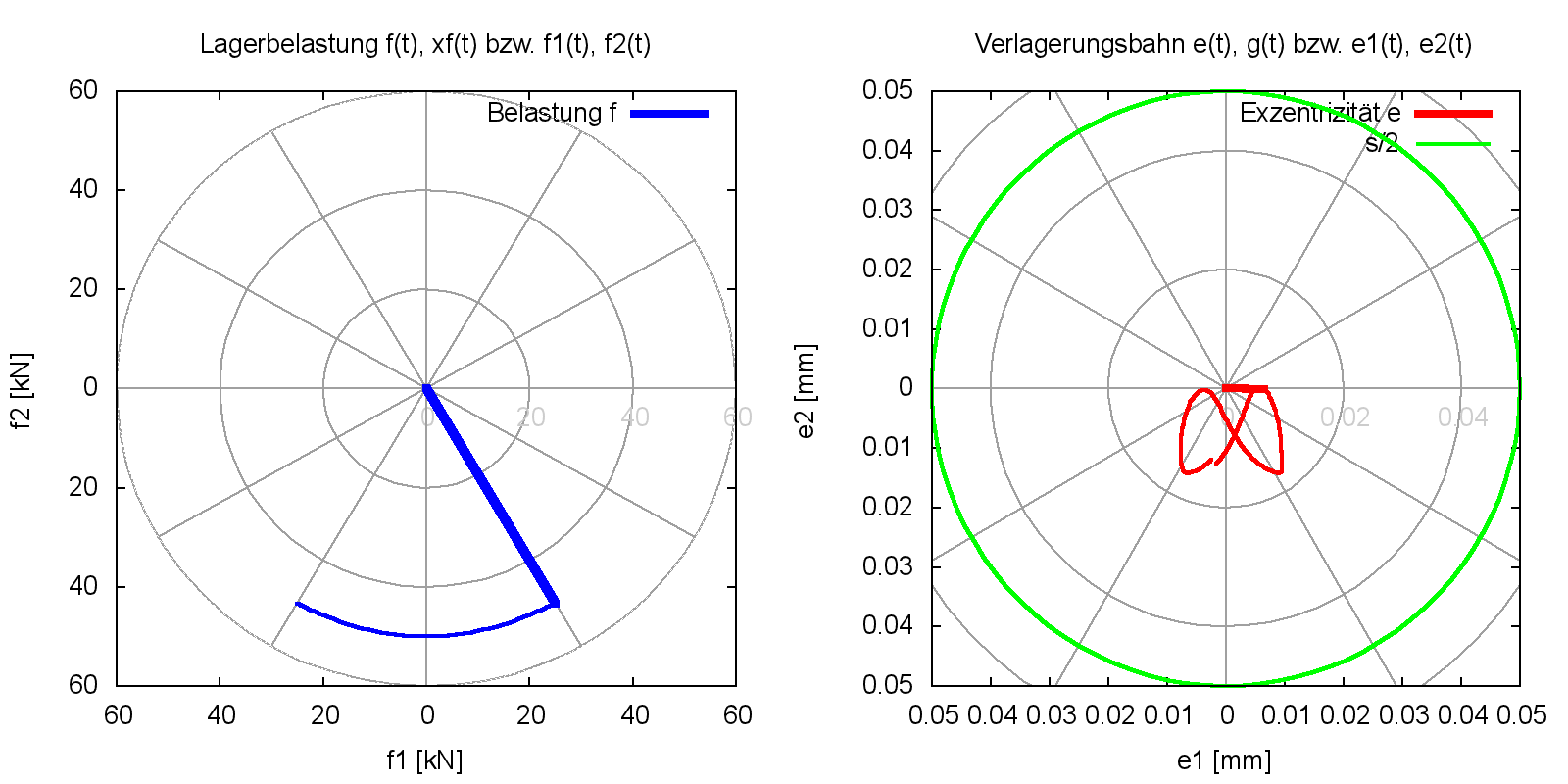
Wegen der versetzten Lagerabschnitte, kann man hier nicht von der Größe der gezeigten mittleren Exzentrizität auf die minimale Schmierspalthöhe schließen, die für die Lagertragfähigkeit die eigentlich entscheidende Größe darstellt. Deshalb ist hier das Diagramm im Bild 4.111 mit dem Verlauf der Exzentrizität e und der minimalen Schmierspalthöhe hMin aufschlussreicher.

Die Animationen zu den Bildern 4.112 und 4.113 zeigen die Druckverteilungen p im Schmierspalt, die Spalthöhen h und die Verteilung der Schmierflüssigkeit im Schmierspalt h·F über eine Pendelbewegung. In den 2-d-Darstellungen des Bildes 4.112 werden dabei synchron die zwei ausgewählten Lagerquerschnitte JZ=11 und JZ=30 gezeigt, die etwa in der Mitte der beiden versetzten Lagerabschnitte liegen.
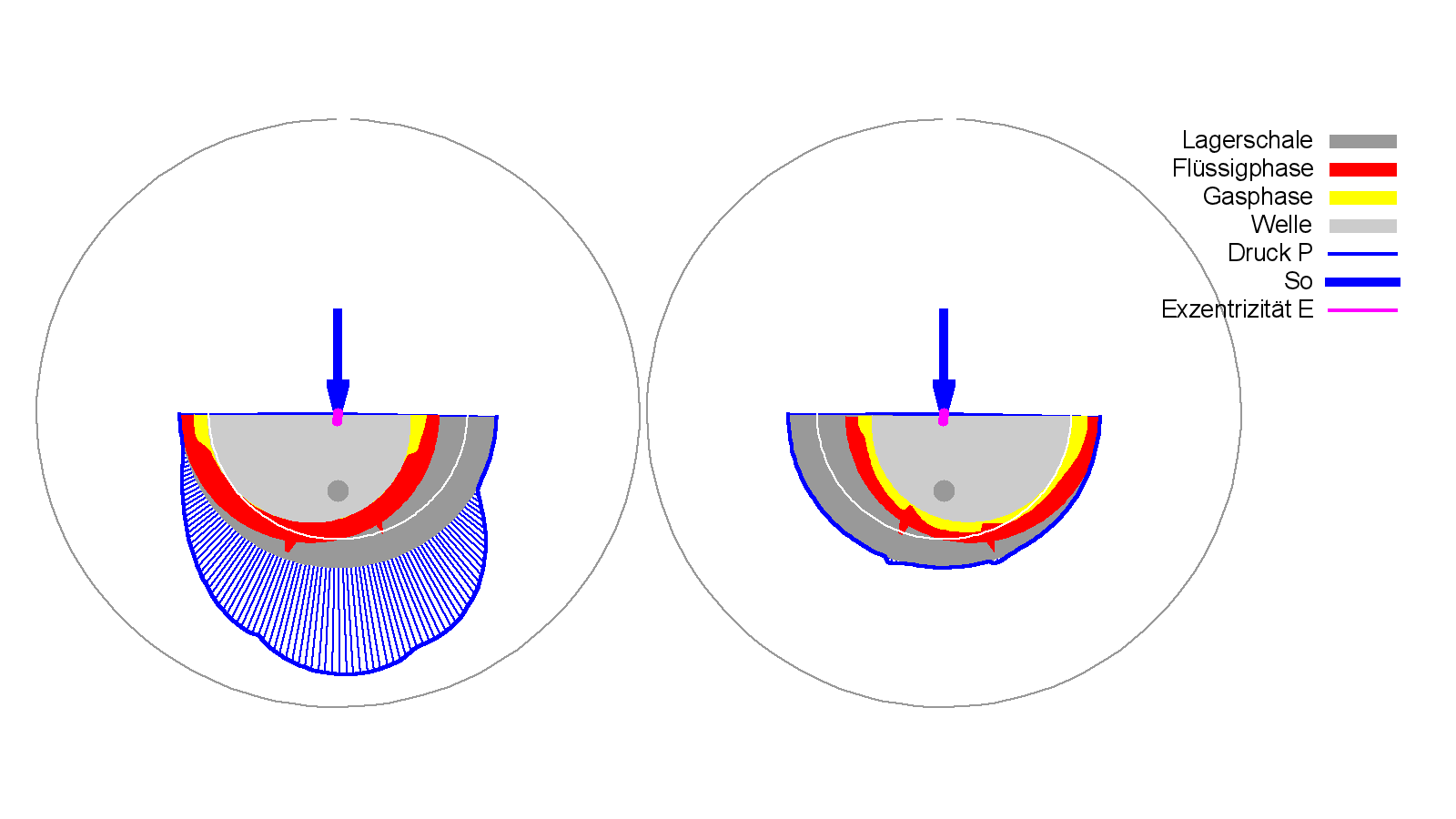
Bild 4.112: Dimensionslose Druckverteilung P, Spaltgeometrie H und Schmierflüssigkeitsverteilung HF zum Zeitpunkt JT=46 des Demonstrationsbeispiels Demo14 (Bilddatei: Demo14-2d-Pol-P-H-HF-JZ=11-JZ=30-JT=201.png) (Animation: Demo14-2d-Pol-P-H-HF-JZ=11-JZ=30.wmv)
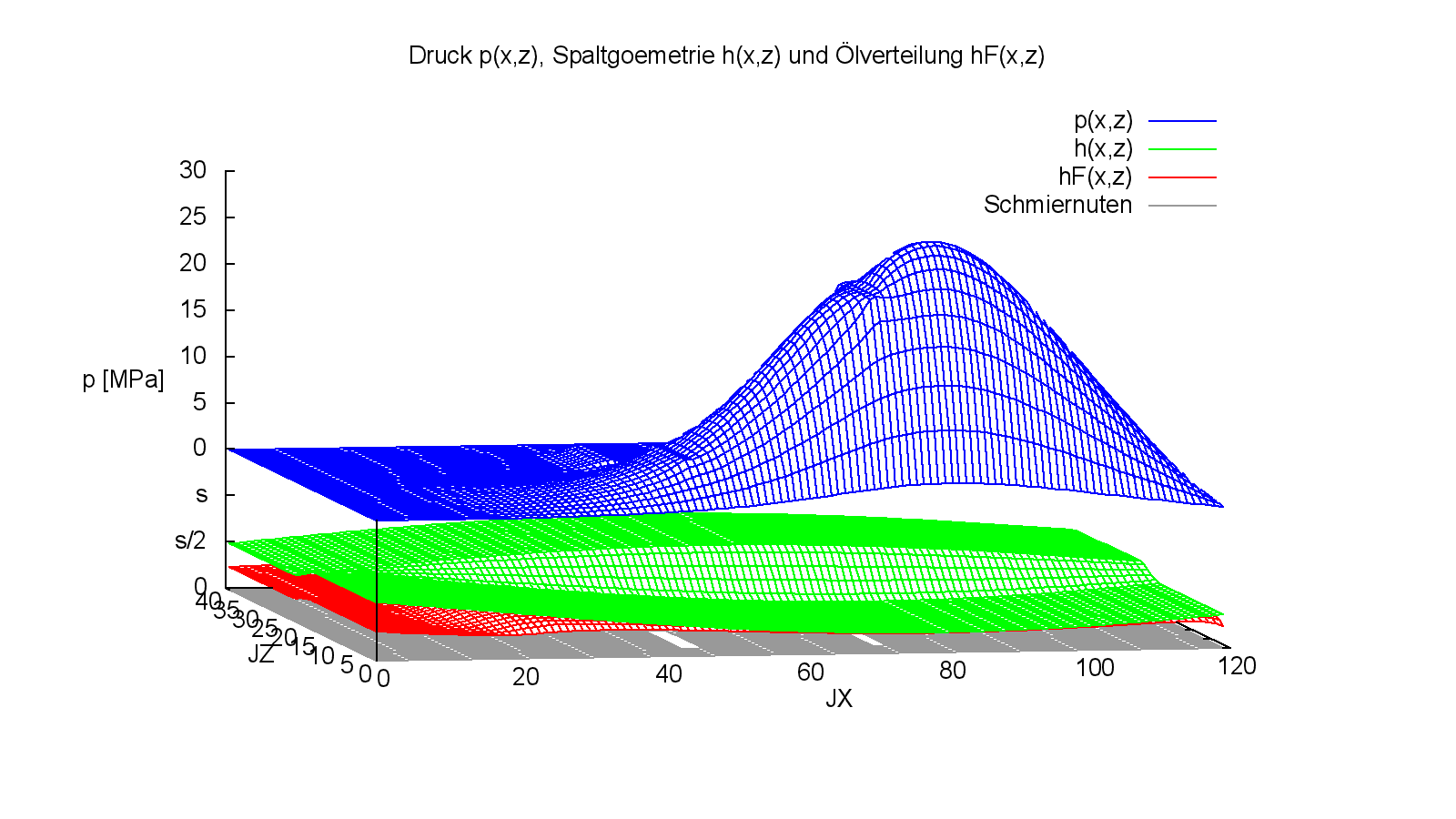
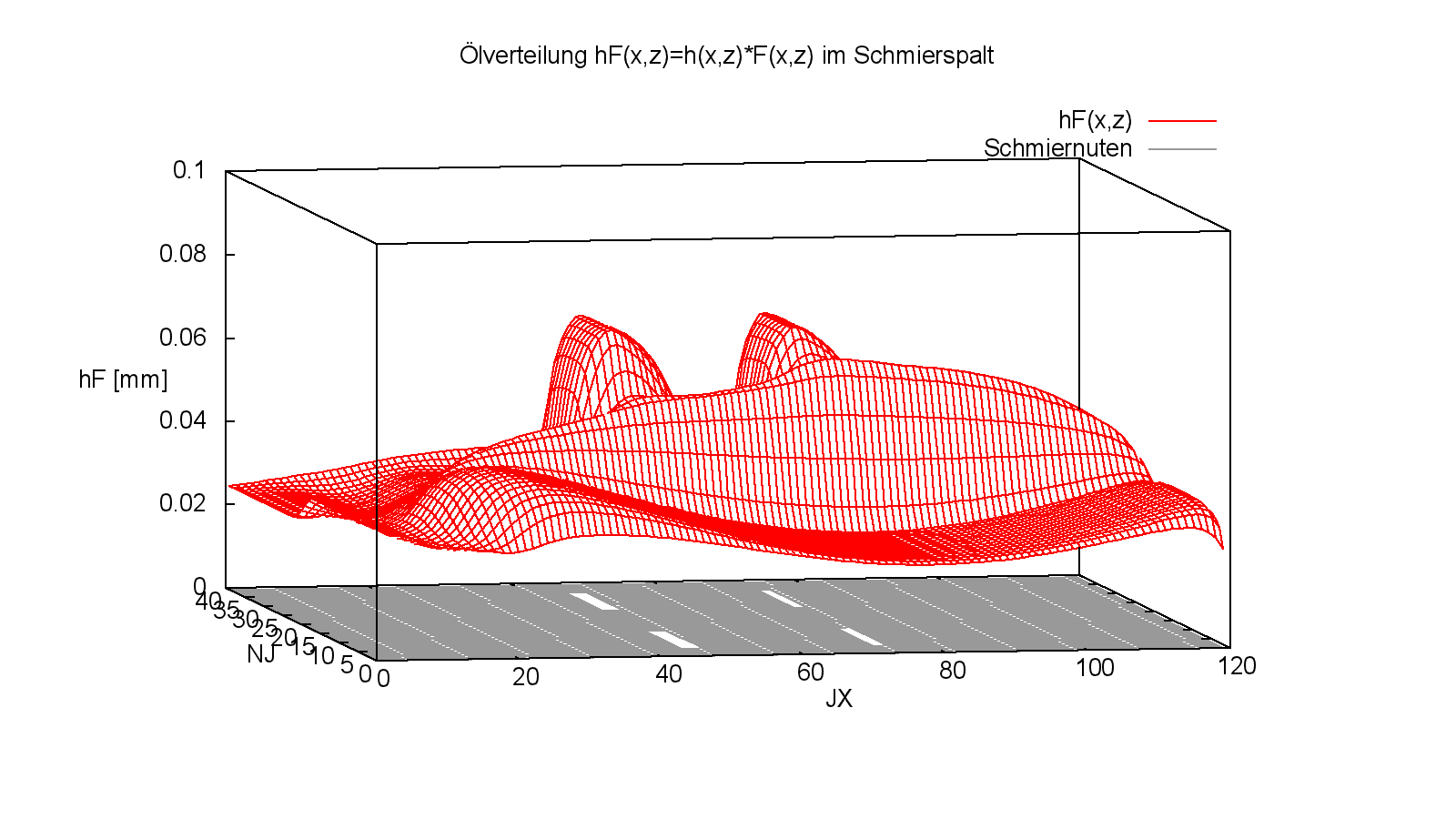
Die Bilder 4.114 und 4.115 mit den zugehörigen Animationen geben einen noch deutlicheren Einblick in die Strömungsverhältnisse der Schmierflüssigkeit im Schmierspalt, die in diesem Beispiel von besonderem Interesse sind.

Hinweis zur Überwindung des Startproblems der Berechnung: Wenn Du versuchst, dieses Demonstrationsbeispiel nachzurechnen, wirst Du feststellen, dass die Berechnung beim 1.Zeitschritt instabil ist. Das Programm liefert folgende Anzeige:
====================================================================== SOLVER: Berechnung ausfuehren ====================================================================== -1- Komplette Berechnung von JT= 1 bis 401 ausfuehren -2- Berechnung ueber ein Zeitintervall JT= 1 bis NT3 ausfuehren -a- Zurueck zum PreProzessor (Eingabedaten bearbeiten)Weiter zum PostProzessor (Ergebnisse auswerten und sichern) Eingabe: 1 Routine: VerlagBahn2 Berechnung des Druckverlaufs P(Z,X,T) ueber 400 Zeitschritte DE1 DE2 DF1 DF2 JT= 2 1 0.0000 0.0000 -0.0042 -0.1973 Extrapolation 2 0.0084 0.1956 0.4884 16.7487 Iteration 3 -0.0033 -0.0038 0.2501 16.8106 Iteration 4 -0.0034 -0.0669 0.0090 3.3059 Iteration 5 0.0033 0.0035 0.0721 3.4628 Iteration 6 0.0020 -0.0211 0.0585 1.4150 Iteration 7 -0.0035 0.0265 0.0498 4.0375 Iteration 8 -0.0006 -0.0070 0.0305 3.3027 Iteration 9 -0.0061 -0.1114 0.0007 -0.1788 Iteration 10 -0.1145 0.1098 -4.6308 6.8398 Iteration FEHLEMELDUNG 302: Abbruch der Iteration wegen Divergenz bei JT= 2 Soll trotzdem mit dem naechsten Zeitschritt fortgefahren werden? -j- Weiterrechnen N e i n, Berechnung abbrechen. Eingabe: n
Das Lösungsverfahren ist mit dem Sprung von einer Anfangslagerbelastung f(JT=1) 0 auf f(JT=1)=5 kN offenbar überfordert und reagiert mit Nicht-Konvergenz. Ein kleiner Trick hilft in diesem Fall einfach über diese Hürde:
Bestätige den Abbruch der Berechnung mit <n> und gehe zurück in den PreProzessor in das 2. Hauptmenü "Festlegungen zur Theorie, zum Berechnungsverlauf und zum Lagertyp" und ändere den Steuerparameter von Thoe=2 auf Theo=1. Nun wird das Programm mit der klassischen Reynoldsschen Differentialgleichung arbeiten. Da diese Differentialgleichung linear ist und deshalb direkt gelöst werden kann, ist sie unanfälliger gegen große Drucksprünge.
Klicke Dich nun durch die Hauptmenüs des PreProzessors bis zum Menü "Festlegen der Anfangsdruckverteilung" und wähle die Aktion -1- "Anfangsdruckverteilung auf Standardanfangsdruck zurücksetzen".
Gehe nun weiter in den Solver und starte die Berechnung erneut. Dieses Mal aber nur für 2 Zeitschritte.
====================================================================== SOLVER: Berechnung ausfuehren ====================================================================== -1- Komplette Berechnung von JT= 1 bis 401 ausfuehren -2- Berechnung ueber ein Zeitintervall JT= 1 bis NT3 ausfuehren -a- Zurueck zum PreProzessor (Eingabedaten bearbeiten)Weiter zum PostProzessor (Ergebnisse auswerten und sichern) Eingabe: 2 Festlegen des letzten zu berechnenden Zeitpunktes NT3 -...- NT3 eingeben. 1 < NT3 <= 401 < z > Abbruch, z u r u e c k zum Hauptmenu Eingabe: 3 Routine: VerlagBahn1 Berechnung des Druckverlaufs P(Z,X,T) ueber 2 Zeitschritte DE1 DE2 DF1 DF2 JT= 2 1 0.0000 0.0000 -0.0300 -0.0879 Extrapolation 2 0.0014 -0.0011 -0.0067 0.1292 Iteration 3 0.0003 -0.0027 -0.0009 0.0088 Iteration DE1 DE2 DF1 DF2 JT= 3 1 0.0017 -0.0038 -0.0020 0.0179 Extrapolation 2 0.0001 -0.0004 -0.0001 0.0006 Iteration ---------------------------------------------------------------------- Aktuelle zeitvariable Eingabe- und Ergebnisdaten JT hMin t omega e xe f mm s grd/s mm grd kN 1 0.0400 0.0000 3141.5940 0.0100 0.0000 50.0000 2 0.0394 0.0003 3140.0437 0.0098 0.4898 49.9996 3 0.0388 0.0006 3135.3945 0.0096 1.0334 49.9983 mm s grd/s mm grd kN JT hMin t omega e xe f Aktuelle zeitvariable Eingabe- und Ergebnisdaten
Nachdem das Programm die erfolgreiche Ausführung dieser 2 Zeitschritte angezeigt hat, gehe erneut in den PreProzessor in das 2. Hauptmenü und setze Theo=1 wieder zurück auf Theo=2.
Klicke Dich nun durch den gesamten PreProzessor, bis Du wieder im Solver angekommen bist. Starte nun die Berechnung erneut, aber dieses Mal mit der Aktion -3- "Restliche Berechnung von JT= 3 bis 401 ausführen". Nun müsste die Berechnung erfolgreich durchlaufen.
Wenn Du nicht gleich die komplette Berechnung ausführen möchtest, kannst Du alternativ auch mit der Aktion -2- starten. Als Anfangszeitpunkt darf dann aber nicht NT1=1 gewählt werden, sondern NT1=3, weil sonst die Berechnung des 1.Zeitschritts erneut ausgeführt wird und die Nicht-Konvergenz erneut auftritt.
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo21.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:

Die im Bild 2.070 skizzierte Variante eines komplexen Schmiermittel-Versorgungssystems wurde nicht aus einer technischen Zweckmäßigkeit heraus entwickelt, sondern um innerhalb der Programmdokumentation in einem Bild zu zeigen, welche Gestaltungsmöglichkeiten des Schmiermittel-Versorgungssystems das Programm SIRIUS bereitstellt. Später kam die Idee, einmal zu testen, ob dieses Schmiersystem auch eine realisierbare Variante darstellt. Nach Belegung der verschiedenen Geräte mit geeigneten technischen Parametern ergab dieses Schmiersystem ein tragfähiges hydrostatisches Lager.
Die Angaben des folgenden Hauptmenüs beschreiben das periphere Schmiermittelversorgungssystem sowohl qualitativ als auch quantitativ:
----------------------------------------------------------------------
Universal-Schmiermittel-Versorgungssystem
----------------------------------------------------------------------
NPu = 3 Anzahl der Schmiermittelpumpe
NTa = 6 Anzahl der Schmiertaschen
NVe = 7 Anzahl der Verbindungsleitungen
NVar= 6 Anzahl der Geraetevarianten
P u m p e n :
max.Pumpendruck max. Oelstrom
JPu pPuMax(JPu) qPuMax(JPu)
1 10.0000 MPa 2.0000 L/min
2 10.0000 MPa 2.0000 L/min
3 10.0000 MPa 2.0000 L/min
G e r a e t e v a r i a n t e n in den Verbindungsleitungen:
1 Nur Kapillare bzw. Leitungswiderstand
1 1 ccp =10000.0000 mm^-3 Widerstandsbeiwert
2 Kapillare und Rueckschlagventil
2 1 ccp =10000.0000 mm^-3 Widerstandsbeiwert
3 Blende und Kapillare in Reihe
3 1 ccp = 2000.0000 mm^-3 Widerstandsbeiwert Kapillare
3 2 cbl = 0.0500 (L/min)^2/MPa Blendenbeiwert
4 Blende, Kapillare und Rueckschlagventil in Reihe
4 1 ccp = 2000.0000 mm^-3 Widerstandsbeiwert Kapillare
4 2 cbl = 0.0500 (L/min)^2/MPa Blendenbeiwert
5 Nur PM-Regler
5 1 q0 = 0.1500 L/min Oelstrom durch Regler bei Taschendruck PTa=0
5 2 qP = 0.3000 L/min Theoretischer Oelstrom bei Taschendruck PTa=PP
5 3 pP = 10.0000 MPa Pumpendruck bei Aufnahmen der Kennlinie
5 4 pS = 1.0000 MPa Differenz zwischen Pumpendruck PPu und Druck im Kennlinien-Scheitelpunkt S
5 5 eta0 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers bei Aufnahme der Kennlinie
5 6 eta1 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers im Betriebszustand
5 qP1 = 0.3000 L/min Theoretischer Oelstrom bei Taschendruck PTa=PPu
5 cpm = 0.0150 L/min/MPa Anstieg der Kennlinie im aufsteigenden Ast
5 rpm = 3.5088 MPa*min/L Stroemungswiderstand des vollstaengig geoeffneten PM-Reglers
6 PM-Regler und Rueckschlagventil
6 1 q0 = 0.1500 L/min Oelstrom durch Regler bei Taschendruck PTa=0
6 2 qP = 0.3000 L/min Theoretischer Oelstrom bei Taschendruck PTa=PP
6 3 pP = 10.0000 MPa Pumpendruck bei Aufnahmen der Kennlinie
6 4 pS = 1.0000 MPa Differenz zwischen Pumpendruck PPu und Druck im Kennlinien-Scheitelpunkt S
6 5 eta0 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers bei Aufnahme der Kennlinie
6 6 eta1 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers im Betriebszustand
6 qP1 = 0.3000 L/min Theoretischer Oelstrom bei Taschendruck PTa=PPu
6 cpm = 0.0150 L/min/MPa Anstieg der Kennlinie im aufsteigenden Ast
6 rpm = 3.5088 MPa*min/L Stroemungswiderstand des vollstaengig geoeffneten PM-Reglers
V e r b i n d u n g s l e i t u n g e n :
JVe Nummer der Verbindungsleitung
JPu Nummer der verbundenen Pumpe
JVar Nummer der Geraetevariante in der Leitung
JTa Nummer der verbundenen Schmiertasche
Typ Nummer des Geraetetyps
JVe JPu JVar JTa Typ Bezeichnung des Geraetetyps
1 1 >-- 2--< 2 2 Kapillare und Rueckschlagventil
2 1 >-- 1--< 3 1 Nur Kapillare bzw. Leitungswiderstand
3 2 >-- 5--< 3 3 Nur PM-Regler
4 2 >-- 6--< 4 4 PM-Regler und Rueckschlagventil
5 1 >-- 4--< 5 6 Blende, Kapillare und Rueckschlagventil in Reihe
6 2 >-- 5--< 6 3 Nur PM-Regler
7 3 >-- 3--< 6 5 Blende und Kapillare in Reihe
Bild 4.130 zeigt die Druckverteilung über den Umfang der Welle in Lagermitte bei konzentrischer Lage der Welle.

Bild 4.130: Druckverteilung über den Umfang in Lagermitte bei konzentrischer Wellenlage des Demonstrationsbeispiels Demo21 (Bilddatei: Demo21-Dim-2d-Abw-p-h-JT=21-JZ=1.png)
Dazu wurde auch noch eine Variante berechnet mit einer vorgegebenen Lagerbelastung 15 kN. Bild 4.131 zeigt dazu die Druckverteilung über den Lagerumfang.
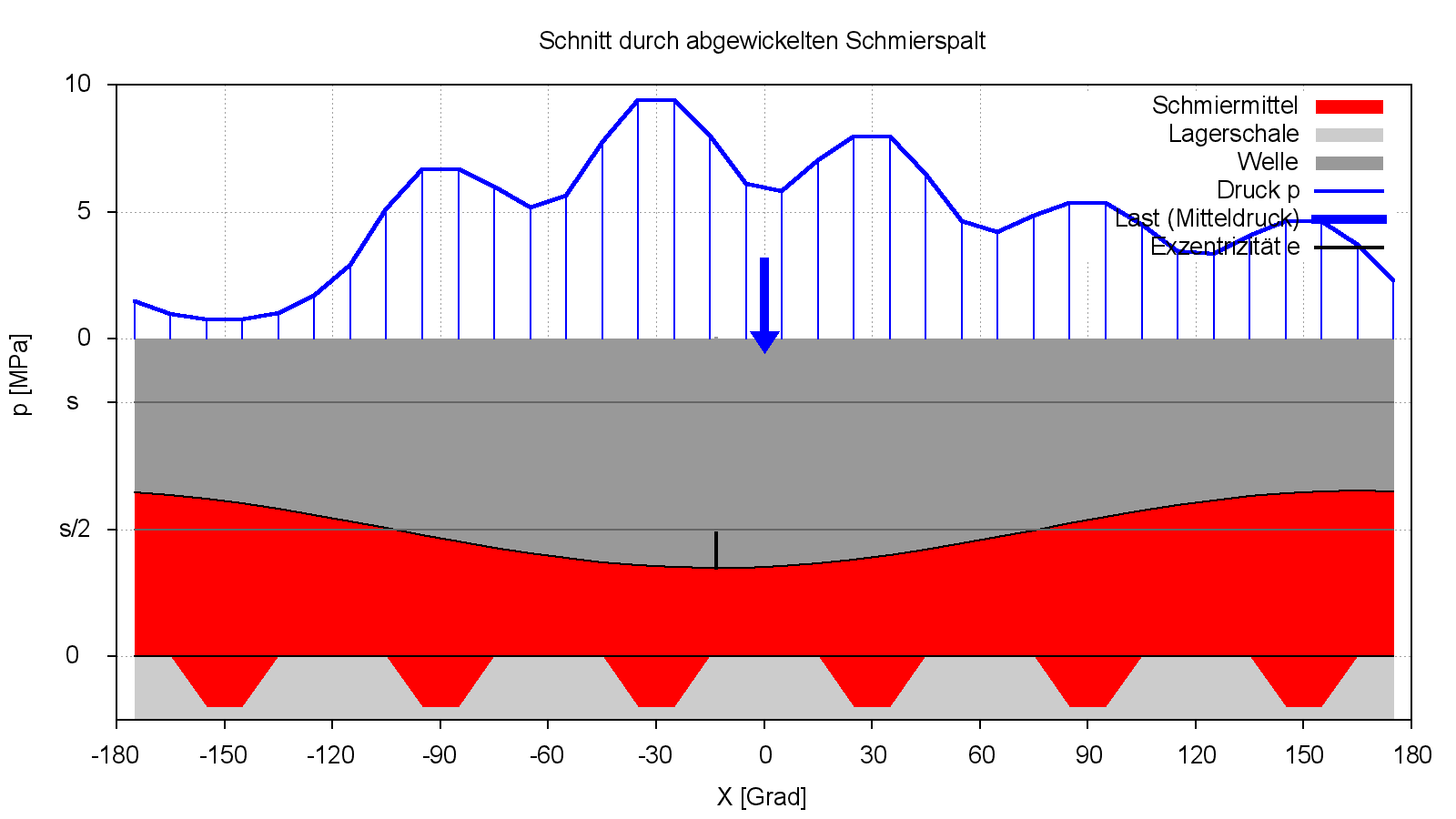
Bild 4.131: Druckverteilung über den Umfang in Lagermitte bei vorgegebener Lagerbelastung des Demonstrationsbeispiels Demo21-1 (Bilddatei: Demo21-1-Dim-2d-Abw-p-h-JT=21-JZ=1.png)
Gegenüber der Ausgangsvariante "Demo21" sind für die Variante "Demo21-1" folgende Eingabedaten zu ändern:
| Steuerparameter | Last=1 | wird zu | Last=2 | Hauptmenü: "Festlegungen zur Theorie, ... " | |
| Lagerbelastung | f=0 | wird zu | f=15 kN | Hauptmenü: "Eingeben ... der konstanten Parameter" |
Bei der Festlegung der Anfangswerte der Variante Demo21-1 wurde so vorgegangen, dass die Endergebnisse aus Demo21 zu den Anfangswerten von Demo21-1 gemacht wurden (Aktion -3- im Hauptmenü "Festlegen der Anfangsdruckverteilung").
Beim Versuch die Berechnung mit exakt den gleichen Daten nachzuvollziehen, wirst Du feststellen, dass das Programm die Berechnung zum Zeitpunkt JT=3 wegen Nicht-Konvergenz abbrechen und die Frage stellen wird, ob weiter gerechnet werden soll, gemäß nachfolgender Fehlermeldung:
Routine: VerlagBahn2
Berechnung des Druckverlaufs P(Z,X,T) ueber 20 Zeitschritte
DE1 DE2 DF1 DF2 JT= 2
1 0.0000 0.0000 0.1086 -0.9079 Extrapolation
2 -0.0197 0.1527 0.0826 0.0741 Iteration
3 -0.0123 -0.0091 0.0000 -0.0051 Iteration
DE1 DE2 DF1 DF2 JT= 3
1 -0.0320 0.1437 -0.0114 0.4516 Extrapolation
2 -0.0147 -0.1228 -0.2377 -0.3789 Iteration
3 0.0310 0.0549 0.0125 0.0372 Iteration
4 -0.0001 -0.0036 0.0318 0.0558 Iteration
5 0.0007 0.0014 0.0121 0.0211 Iteration
6 -0.0002 -0.0003 0.0391 0.0687 Iteration
7 0.0008 0.0015 0.0178 0.0310 Iteration
8 -0.0003 -0.0005 0.0436 0.0764 Iteration
9 0.0009 0.0018 0.0241 0.0423 Iteration
10 -0.0004 -0.0007 0.0472 0.0827 Iteration
A b b r u c h der Iteration wegen Divergenz bei JT= 3
Soll trotzdem mit dem naechsten Zeitschritt fortgefahren werden?
-j- Weiterrechnen
N e i n, Berechnung abbrechen.
Eingabe:
j
DE1 DE2 DF1 DF2 JT= 4
1 -0.0142 0.0752 0.0685 0.3364 Extrapolation
2 -0.0310 -0.0988 -0.2312 -0.3607 Iteration
3 0.0035 -0.0039 -0.3229 -0.5675 Iteration
Da es sich hier nur um die Anlaufrechnung handelt, kann man zunächst versuchen, durch Eingabe der Antwort "j" die Berechnung trotzdem fortzusetzen in der Hoffnung, dass in den nachfolgenden Zeitschritten doch noch eine Konvergenz gegeben ist. In diesem Fall wird unsere Hoffnung erfüllt und wir erhalten ein brauchbares Endergebnis. Wäre das nicht der Fall, müsste durch andere Maßnahmen für die Konvergenz gesorgt werden. Siehe dazu Abschnitt 4.9.2 "Probleme der Überforderung der Lösungsalgorithmen".
Die primären Eingabe- und Ergebnisdaten zu der Variante des Demonstrationsbeispiels sind in der Datei "Demo21-1.txt" im Verzeichnis "./DatenDemo" abgelegt.
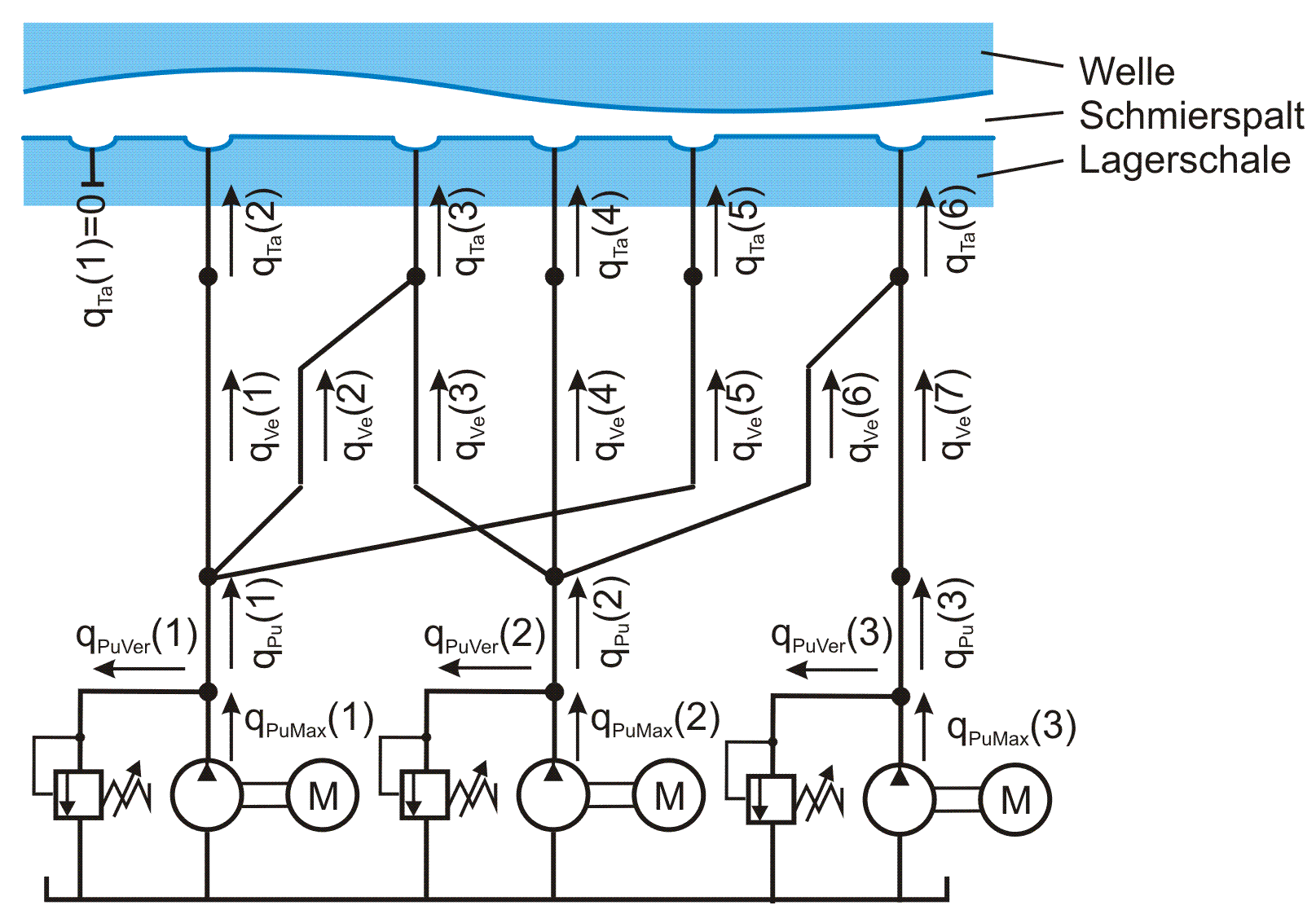
Bild 2.081: Schmiermittelströme im peripheren Schmiersystem
Im Bild 2.081 wird die Zuordnung der einzelnen Schmiermittelströme q... im Schmiersystem darstellt. Es gibt damit eine grafische Interpretationshilfe der folgenden zwei Datentabellen, die der PostProzessor mit den Aktionen -46- und -47- liefert. Die entsprechenden Stromdaten sind gelb hervorgehoben:
Oelstrom- und Leistungsbilanz am Schmierspalt zum Zeitpunkt JT= 21
============================================================================
NTa = 6 Anzahl der Schmiertaschen im Lager
============================================================================
S c h m i e r t a s c h e n
----------------------------------------------------------------------------
JTa Nummer der Schmiertasche
pTa Druck in der Schmiertasche
qTa Oelstrom von den Verbindungsleitungen in die Schmiertasche
leiTa Leistung des Oelstroms in die Schmiertasche
JTa pTa qTa leiTa
[MPa] [L/min] [kW]
1 0.7719 0.0000 0.0000
2 6.6689 0.3997 0.0444
3 9.3975 0.2440 0.0382
4 7.9578 0.2694 0.0357
5 5.3588 0.4419 0.0395
6 4.6141 0.6982 0.0537
----------------------------------------------------------------------------
Summe 2.0531 0.2115
============================================================================
S t r o m b i l a n z
----------------------------------------------------------------------------
Summe qTa 2.0531 L/min ueber die Schmiertaschen zufliessender Oelstrom
-qRand -2.2349 L/min ueber Lagerrand abfliessender Oelstrom
----------------------------------------------------------------------------
=volFlSpalt_t 0.0000 L/min =d(volSpalt*FGes)/dt Fluessigkeitsvolumenaenderung
Differenz -0.1817 L/min =(Summe pTa)-qRand-d(volSpalt*FGes)/dt
rel.Differenz -8.85 % =Differenz/(summe qTa)*100
============================================================================
S p a l t v o l u m e n
----------------------------------------------------------------------------
volSpalt 0.7854 qcm Schmierspaltvolumen
volFlSpalt 0.7795 qcm Volumen der fluessigen Phase im Schmierspalt
FGes 0.9924 Fuellungsgrad des Schmierspalts
============================================================================
R e i b m o m e n t
----------------------------------------------------------------------------
moWe -0.0280 Nm Reibmoment an der Welle
============================================================================
E n e r g i e b i l a n z
----------------------------------------------------------------------------
Summe leiTa 0.2115 kW in die Schmiertaschen zugefuehrte Leistung
-leiRand -0.0037 kW ueber Lagerrand abfliessende Leistung
+leiWe 0.0000 kW durch Reibmoment zugefuehrte mech. Leistung
----------------------------------------------------------------------------
=lreib 0.2223 kW im Schmierspalt in Waerme umgewandelte Leistung
Differenz -0.0145 kW =(Summe leiTa)-leiRand+leiWe-lreib
rel.Differenz -6.51 % =Differenz/lreib*100
============================================================================
Daten des peripheren Schmiersystems zum Zeitpunkt JT= 21 ============================================================================ NPu = 3 Anzahl der Schmiermittelpumpen NTa = 6 Anzahl der Schmiertaschen im Lager NVe = 7 Anzahl Verbindungsleitungen zwischen Pumpen und Schmiertaschen NVar= 6 Anzahl der Geraetevarianten in den Verbindungsleitungen ============================================================================ P u m p e n ---------------------------------------------------------------------------- JPu Nummer der Pumpe pPuMax maximaler Pumpendruck, durch Sicherheitsventil begrenzt pPu aktueller Pumpendruck qPuMax maximaler Pumpenoelstrom qPu aktuell fuer die Schmierung genutzter Pumpenoelstrom qPuVer ueber das Sicherheitsventil abgefuehrter Oelstrom leiPuMax installierte (maximale moegliche) Pumpenleistung leiPu aktuelle Pumpenleistung leiPuVer Verlustleistung des ueber das Sicherheitsventil abgefuehrten Oelstroms JPu pPuMax pPu qPuMax qPu qPuVer leiPuMax leiPu leiPuVer [MPa] [MPa] [L/min] [L/min] [L/min] [kW] [kW] [kW] 1 10.0000 10.0000 2.0000 0.9139 1.0861 0.3333 0.3333 0.1810 2 10.0000 10.0000 2.0000 0.6603 1.3397 0.3333 0.3333 0.2233 3 10.0000 10.0000 2.0000 0.4789 1.5211 0.3333 0.3333 0.2535 ---------------------------------------------------------------------------- Summe 6.0000 2.0531 3.9469 1.0000 1.0000 0.6578 ============================================================================ G e r a e t e v a r i a n t e n in den Verbindungsleitungen: ---------------------------------------------------------------------------- 1 Nur Kapillare bzw. Leitungswiderstand 1 1 ccp =10000.0000 mm^-3 Widerstandsbeiwert 2 Kapillare und Rueckschlagventil 2 1 ccp =10000.0000 mm^-3 Widerstandsbeiwert 3 Blende und Kapillare in Reihe 3 1 ccp = 2000.0000 mm^-3 Widerstandsbeiwert Kapillare 3 2 cbl = 0.0500 (L/min)^2/MPa Blendenbeiwert 4 Blende, Kapillare und Rueckschlagventil in Reihe 4 1 ccp = 2000.0000 mm^-3 Widerstandsbeiwert Kapillare 4 2 cbl = 0.0500 (L/min)^2/MPa Blendenbeiwert 5 Nur PM-Regler 5 1 q0 = 0.1500 L/min Oelstrom durch Regler bei Taschendruck PTa=0 5 2 qP = 0.3000 L/min Theoretischer Oelstrom bei Taschendruck PTa=PP 5 3 pP = 10.0000 MPa Pumpendruck bei Aufnahmen der Kennlinie 5 4 pS = 1.0000 MPa Differenz zwischen Pumpendruck PPu und Druck im Kennlinien-Scheitelpunkt S 5 5 eta0 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers bei Aufnahme der Kennlinie 5 6 eta1 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers im Betriebszustand 6 PM-Regler und Rueckschlagventil 6 1 q0 = 0.1500 L/min Oelstrom durch Regler bei Taschendruck PTa=0 6 2 qP = 0.3000 L/min Theoretischer Oelstrom bei Taschendruck PTa=PP 6 3 pP = 10.0000 MPa Pumpendruck bei Aufnahmen der Kennlinie 6 4 pS = 1.0000 MPa Differenz zwischen Pumpendruck PPu und Druck im Kennlinien-Scheitelpunkt S 6 5 eta0 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers bei Aufnahme der Kennlinie 6 6 eta1 = 50.0000 mPa*s Dynamische Viskositaet am Eingang des PM-Reglers im Betriebszustand ============================================================================ V e r b i n d u n g s l e i t u n g e n ---------------------------------------------------------------------------- JVe Nummer der Verbindungsleitung pVeVer Druckgefaelle von der Pumpe zur Schmiertasche qVe Oelstrom durch die Verbindungsleitung leiVeVer Verlustleistung in der Verbindungsleitung JPu Nummer der verbundenen Pumpe JVar Nummer der Geraetevariante in der Leitung JTa Nummer der verbundenen Schmiertasche JVe pVeVer qVe leiVeVer JPu JVar JTa Bezeichnung des Geraetetyps [MPa] [L/min] [kW] 1 3.3311 0.3997 0.0222 1 >-- 2--< 2 Kapillare und Rueckschlagventil 2 0.6025 0.0723 0.0007 1 >-- 1--< 3 Nur Kapillare bzw. Leitungswiderstand 3 0.6025 0.1717 0.0017 2 >-- 5--< 3 Nur PM-Regler 4 2.0422 0.2694 0.0092 2 >-- 6--< 4 PM-Regler und Rueckschlagventil 5 4.6412 0.4419 0.0342 1 >-- 4--< 5 Blende, Kapillare und Rueckschlagventil in Reihe 6 5.3859 0.2192 0.0197 2 >-- 5--< 6 Nur PM-Regler 7 5.3859 0.4789 0.0430 3 >-- 3--< 6 Blende und Kapillare in Reihe ---------------------------------------------------------------------------- Summe 2.0531 0.1307 ============================================================================ S t r o m b i l a n z ---------------------------------------------------------------------------- Summe qPuMax 6.0000 L/min Bereitgestellter Pumpenstrom (Konstantpumpen) -Summe qPuVer -3.9469 L/min Ueber Druckbegrenzungsventil abgefuehrter Oelstrom ---------------------------------------------------------------------------- =Summe qPu 2.0531 L/min in den Schmierspalt gepumpter Oelstrom =Summe qVe 2.0531 L/min -"- =Summe qTa 2.0531 L/min -"- ============================================================================ E n e r g i e b i l a n z ---------------------------------------------------------------------------- Summe leiPuMax 1.0000 kW Summe der installierten Pumpenleistungen ---------------------------------------------------------------------------- Summe leiPu 1.0000 kW Summe der aktuellen Pumpenleistung -Summe leiPuVer -0.6578 kW Ueber Druckbegrenzungsventil abgefuehrte Leistung ---------------------------------------------------------------------------- =Summe leiVe 0.3422 kW in die Verbindungsleitungen zugefuehrte Leistungen -Summe leiVeVer -0.1307 kW Reibleistungsverluste in den Verbindungsleitungen ---------------------------------------------------------------------------- =Summe leiTa 0.2115 kW in die Schmiertaschen zugefuehrte Leistung ============================================================================zurück weiter
Die primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo22.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
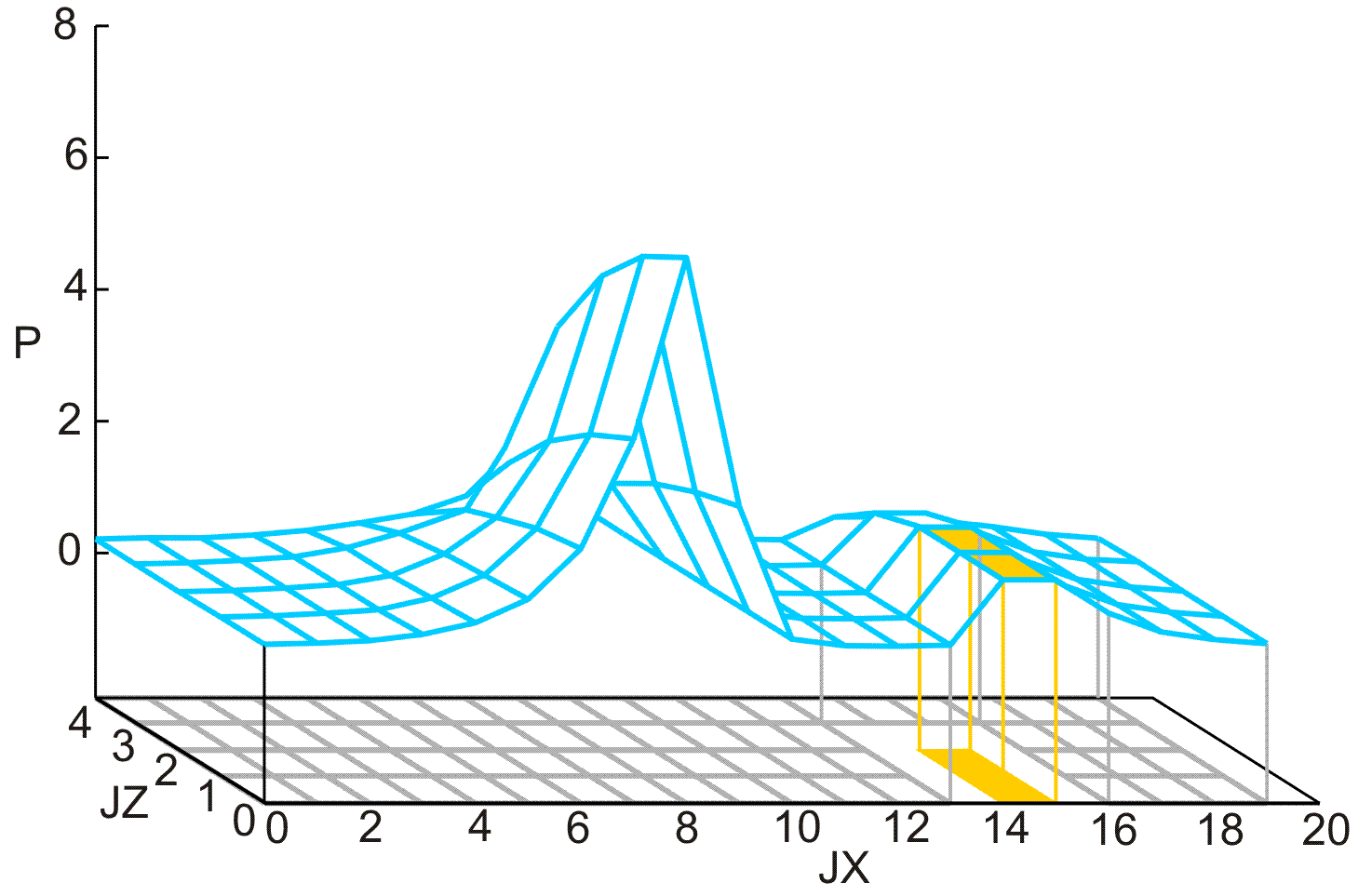
Dieses Demonstrationsbeispiel wurde ausschließlich dazu erzeugt, an einem Beispiel die Diskretisierung der Schmierspaltfläche für die Berechnung der Druckverteilung zu zeigen (siehe dazu Abschnitt 3.4.1.4). Es wurde eine grobe Diskretisierung der Spaltfläche vorgenommen, damit die Gegebenheiten am Spaltelement noch gut erkennbar sind.
zurück weiterDie primären Eingabe- und Ergebnisdaten zu diesem Demonstrationsbeispiel sind in der Datei "Demo23.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
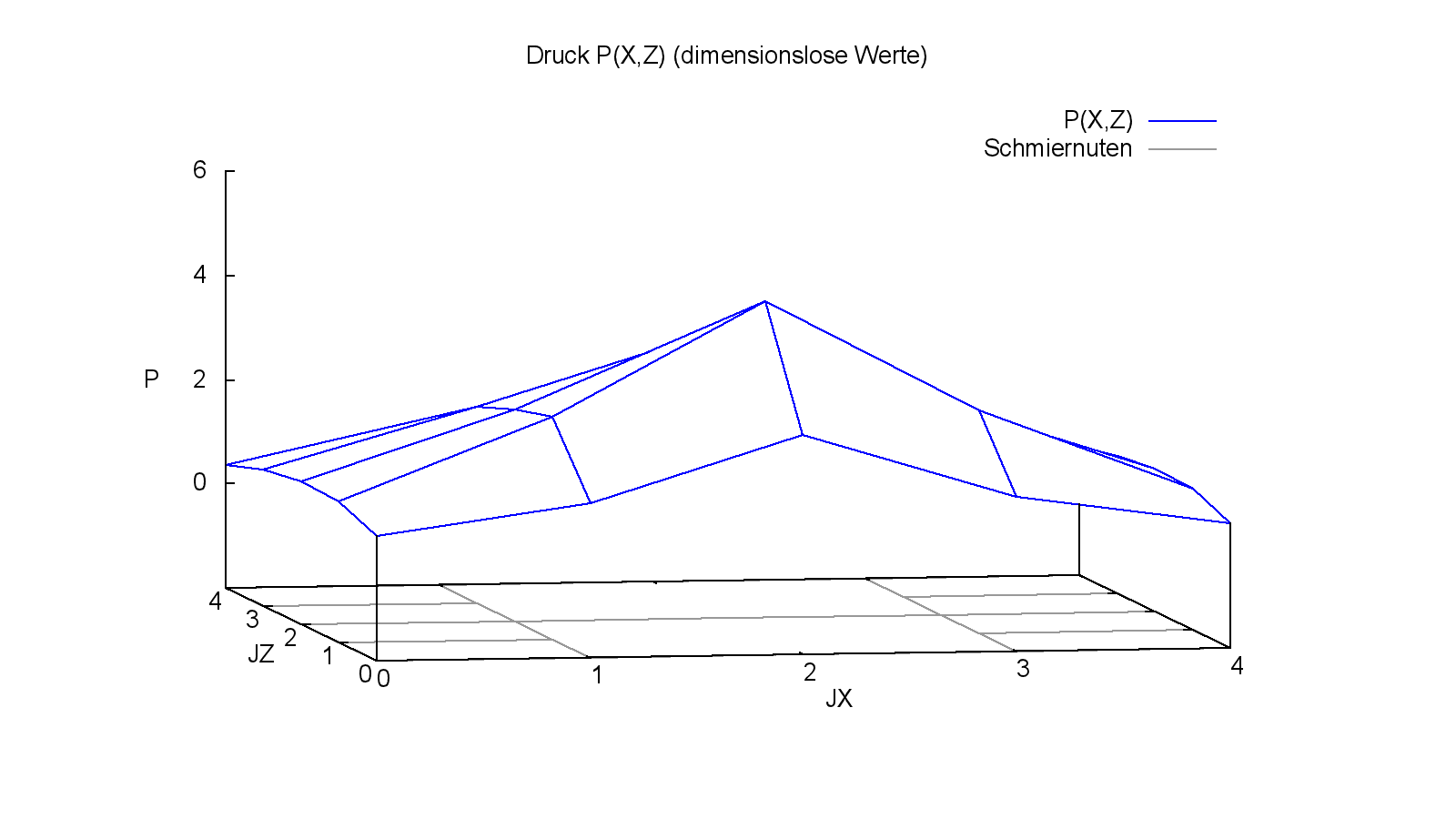
Dieses Demonstrationsbeispiel wurde ausschließlich dazu erzeugt, um an einem Beispiel die Struktur der Koeffizientenmatrix des linearen Gleichungssystems der Hauptrechnung zu zeigen (siehe dazu Abschnitt 3.4.4). Es wurde deshalb eine so extrem grobe Diskretisierung der Spaltfläche vorgenommen, damit die Anzahl der Koeffizienten im Bild 3.41 überschaubar bleibt.
zurück weiterDie primären Eingabe- und Ergebnisdaten der 4 Varianten zu diesem Demonstrationsbeispiel sind in den Dateien "Demo24-1.txt", "Demo24-2.txt", "Demo24-3.txt" und "Demo24-4.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
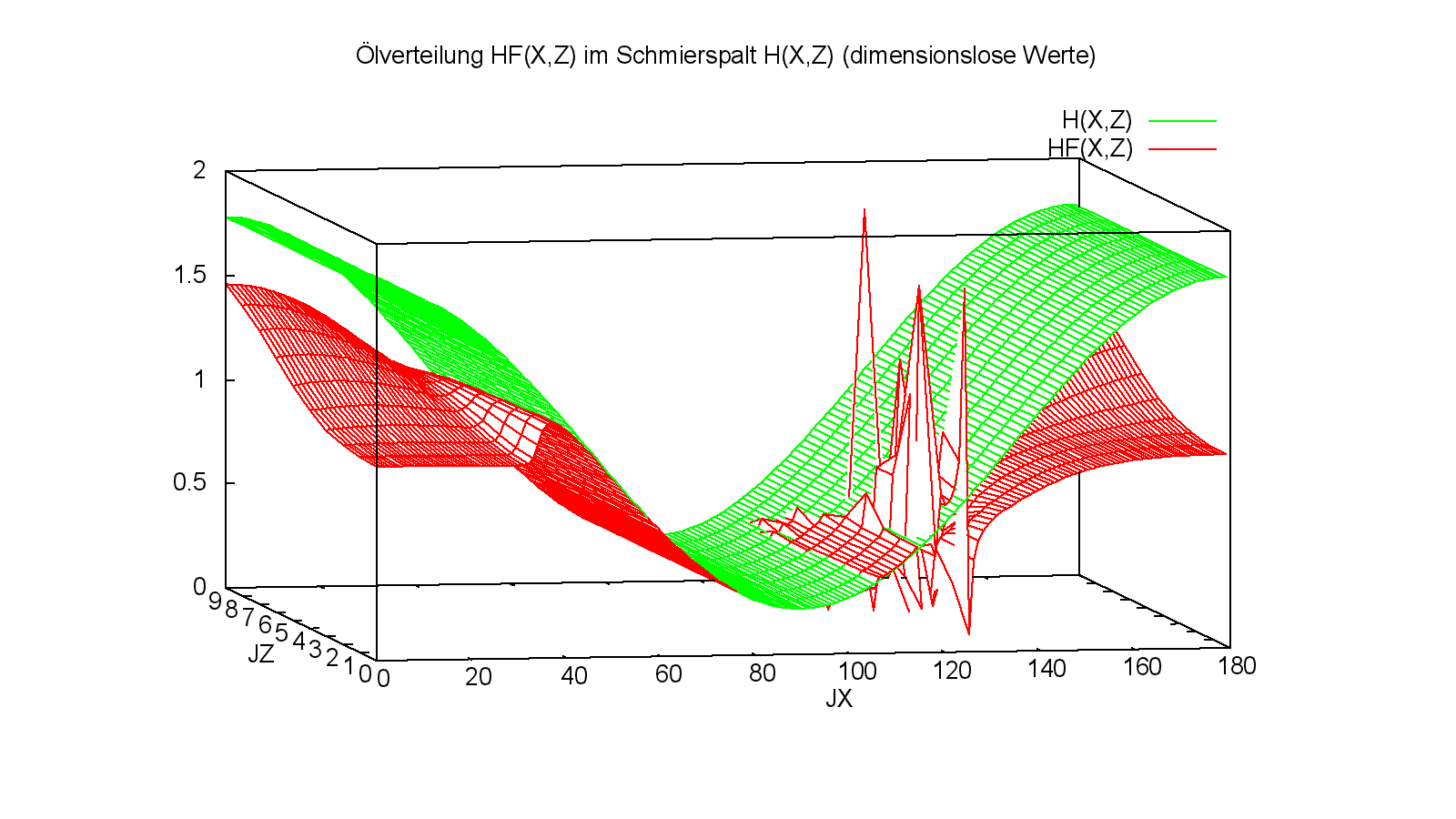
Dieses Demonstrationsbeispiel wurde ausschließlich dazu erzeugt, an einem Beispiel die Wirkungsweise der Korrekturroutinen Pglatt, Fuell1, KleiDru4 und Pkorr6 zur Dämpfung möglicher Instabilitäten der iterativen Berechnung zu demonstrieren. Siehe dazu Abschnitt 3.4.6.
zurück weiterDie primären Eingabe- und Ergebnisdaten der 3 Varianten zu diesem Demonstrationsbeispiel sind in den Dateien "Demo25-1.txt", "Demo25-2.txt" und "Demo25-3.txt" im Verzeichnis "./DatenDemo" abgelegt.
Kurzcharakteristik der Lagervariante:
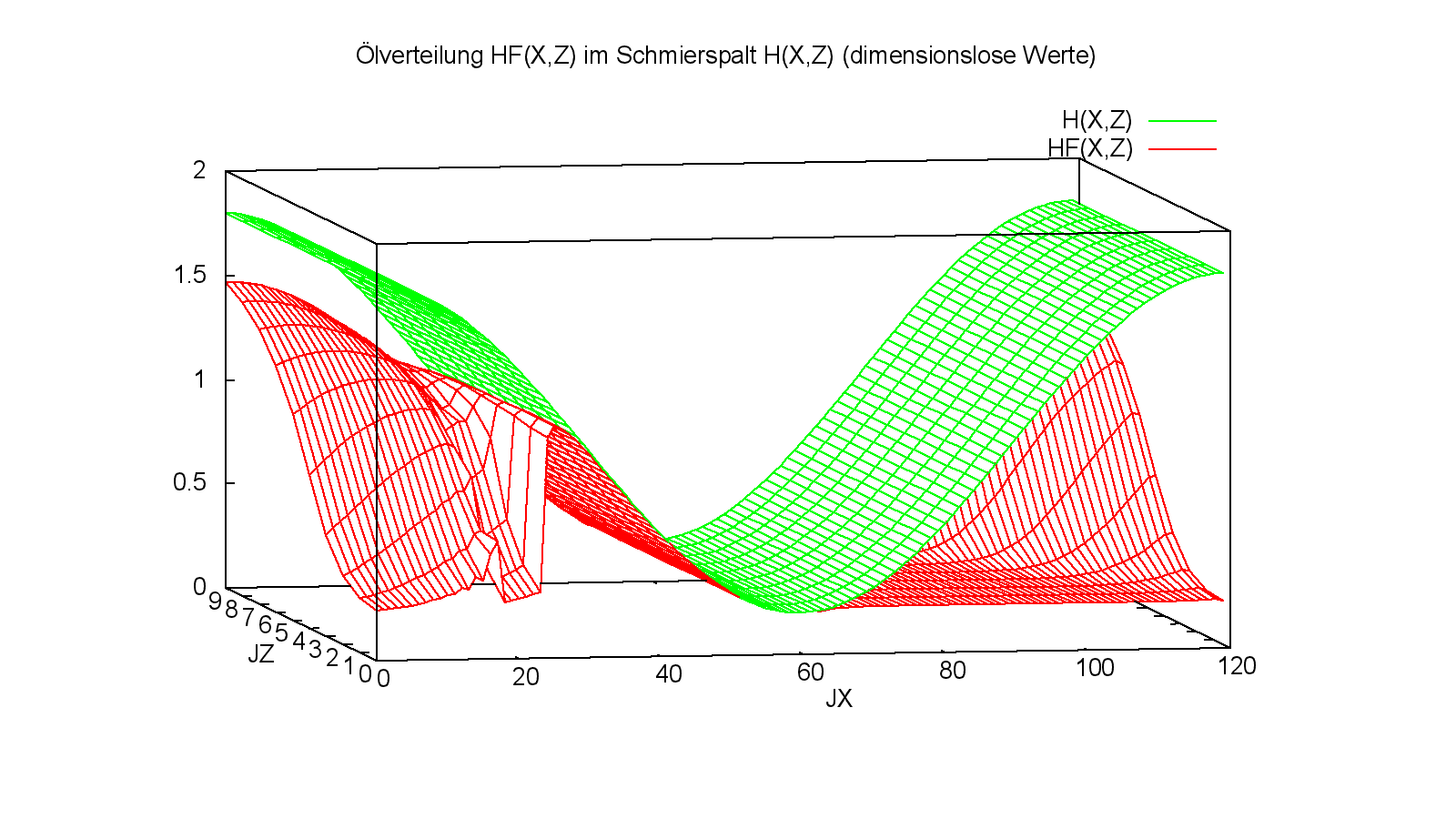
Dieses Demonstrationsbeispiel wurde dazu erzeugt, an einem Beispiel den Umgang mit Instabilitäten der Berechnung zu demonstrieren. Es zeigt eine Instabilität, die trotz der Korrekturroutinen "Pglatt" und "Pkorr6" noch auftreten kann. Siehe dazu Abschnitt 4.9.2.2.
zurück weiter.
.
.