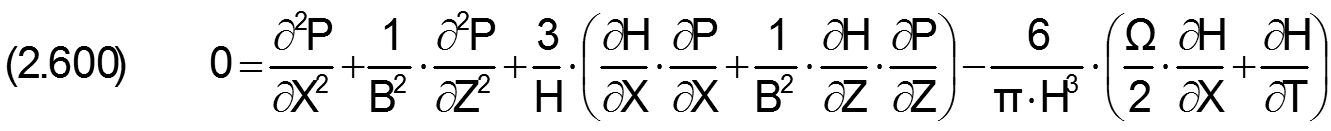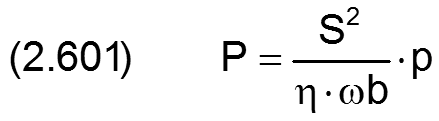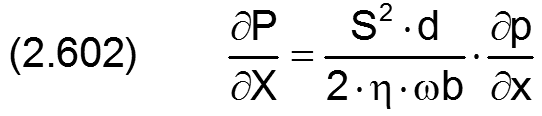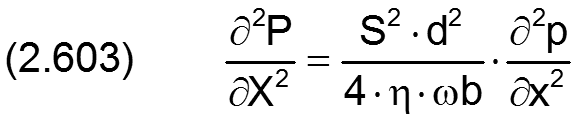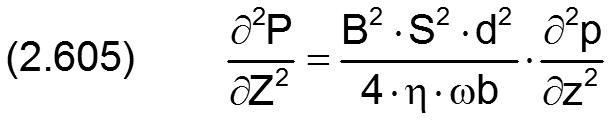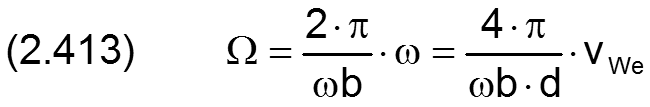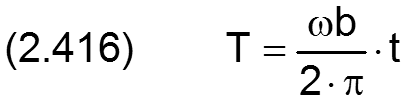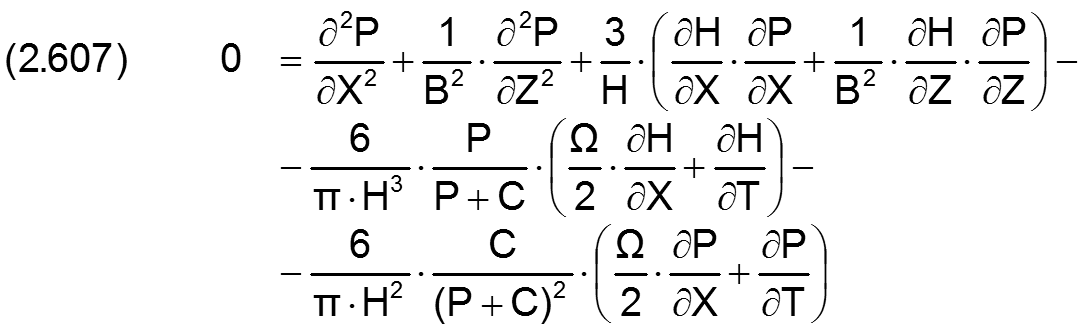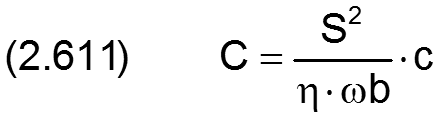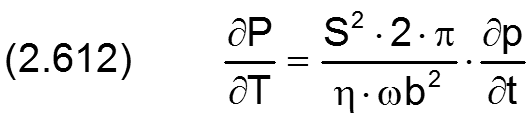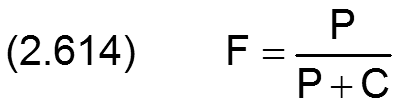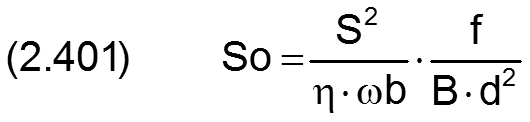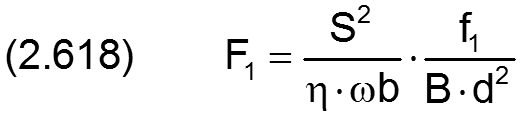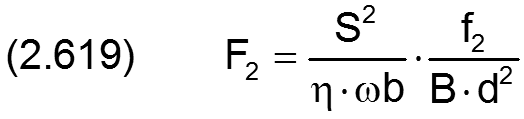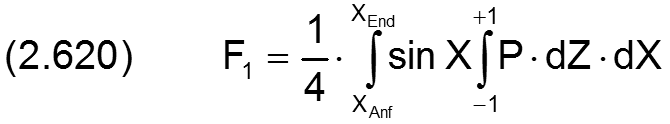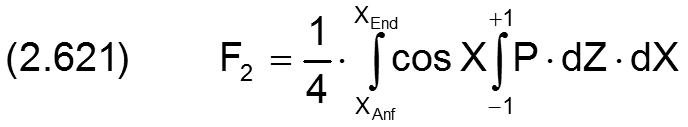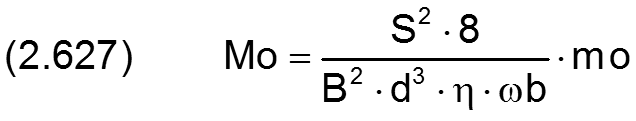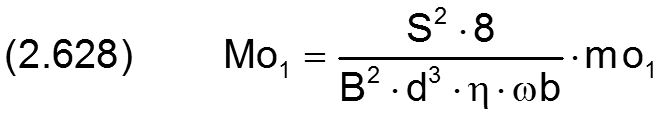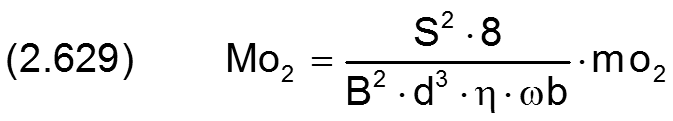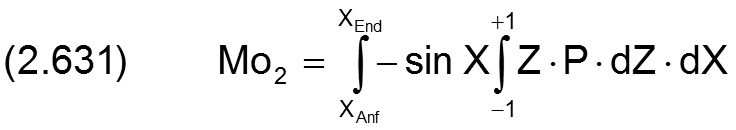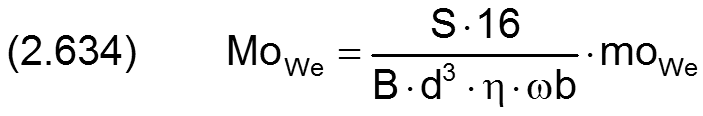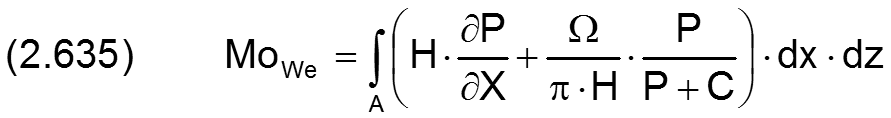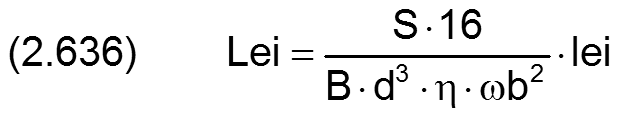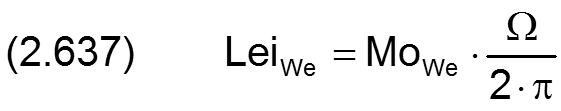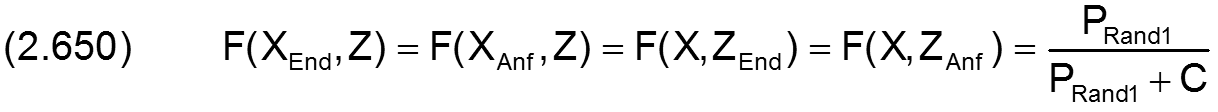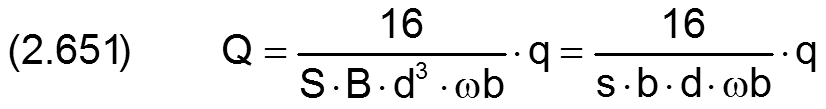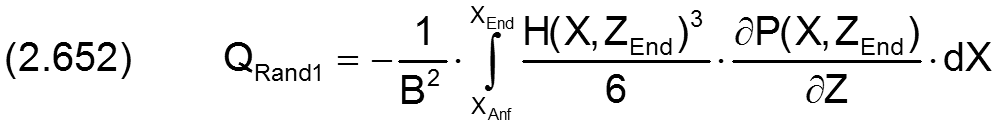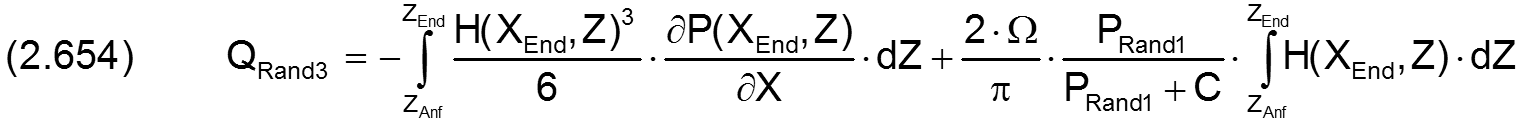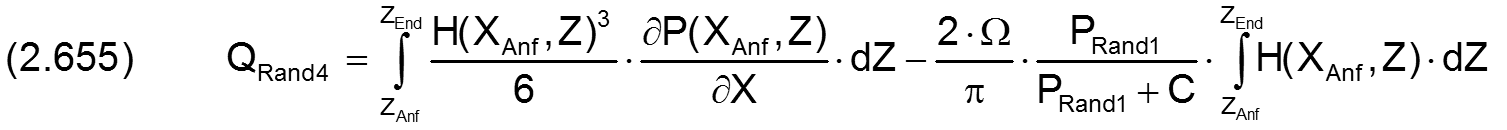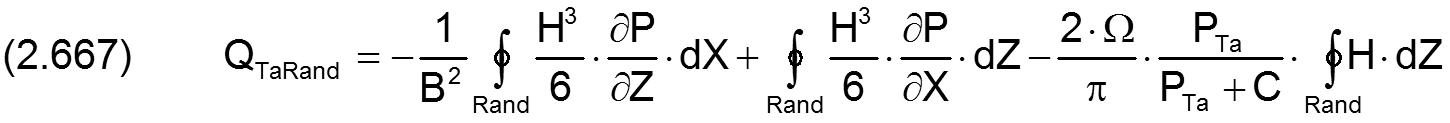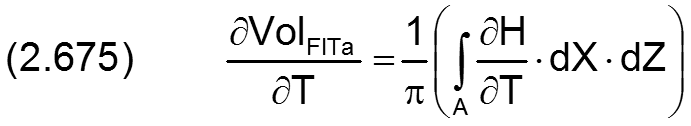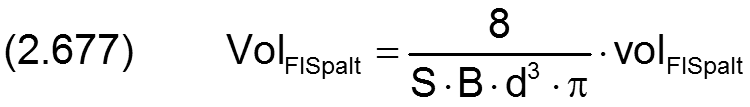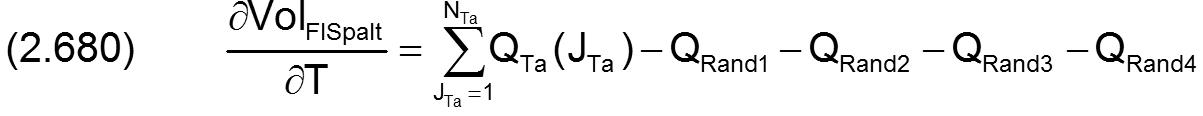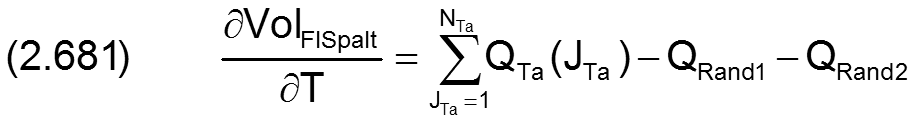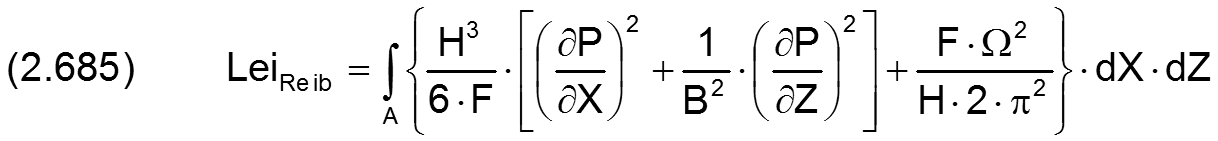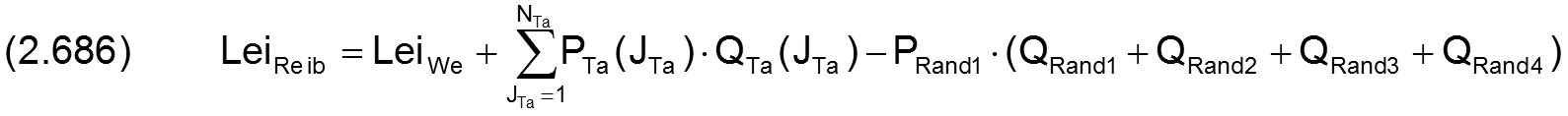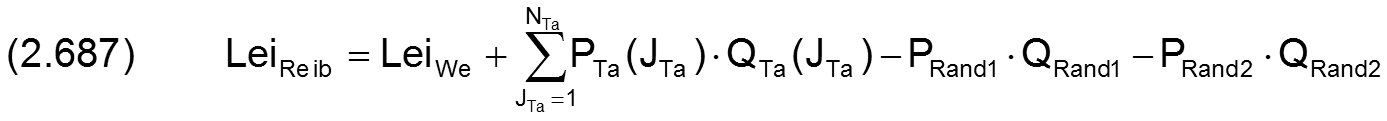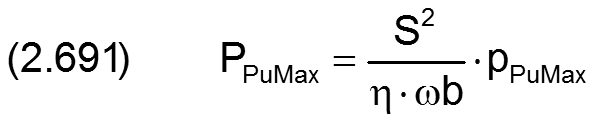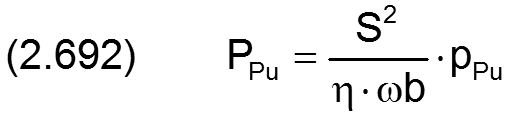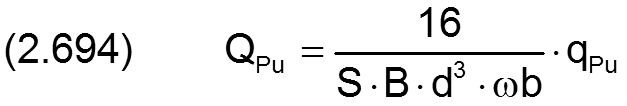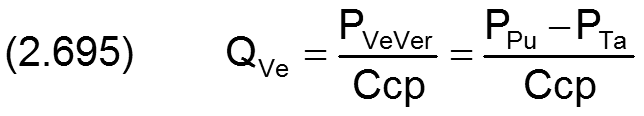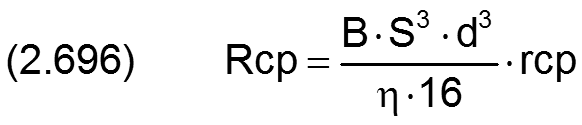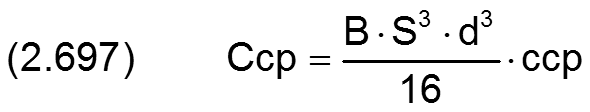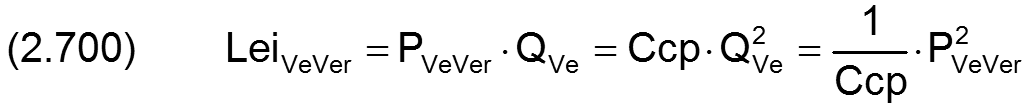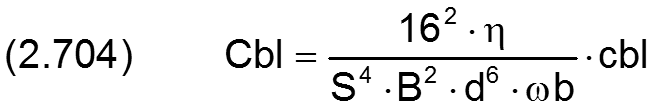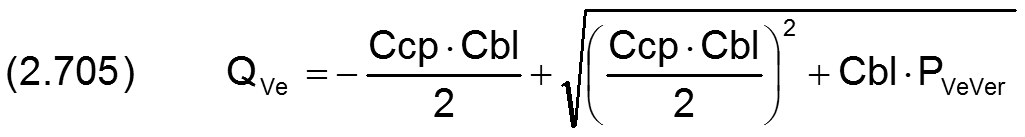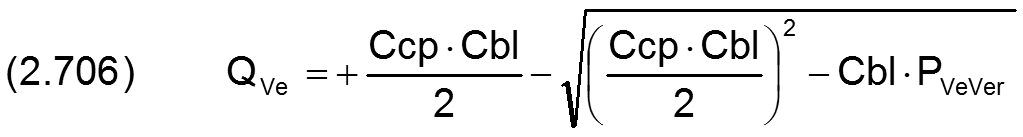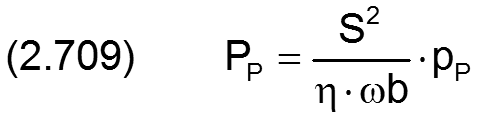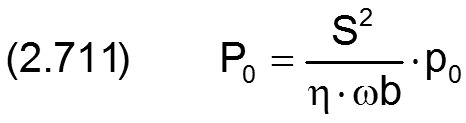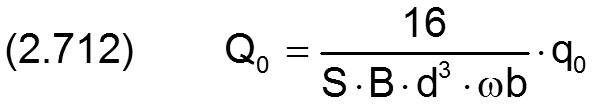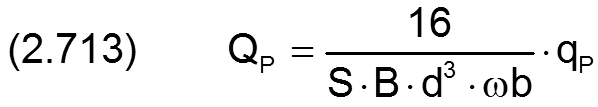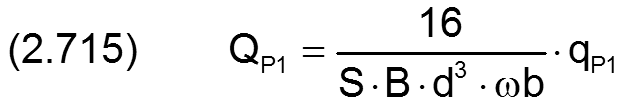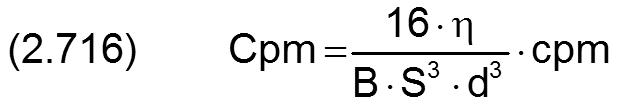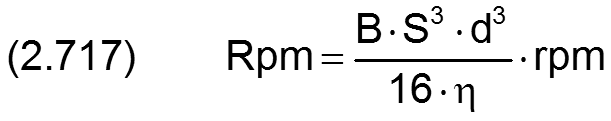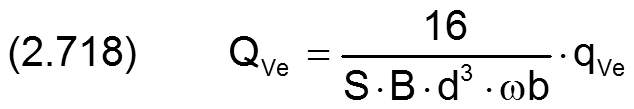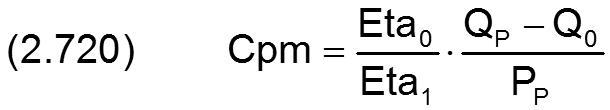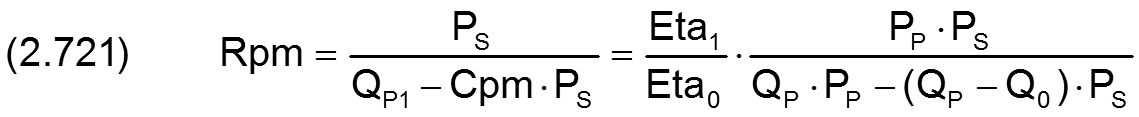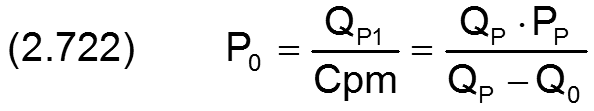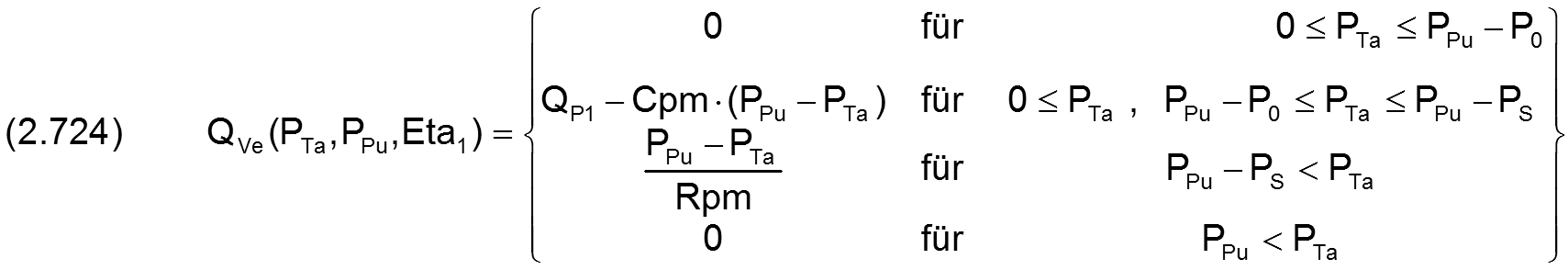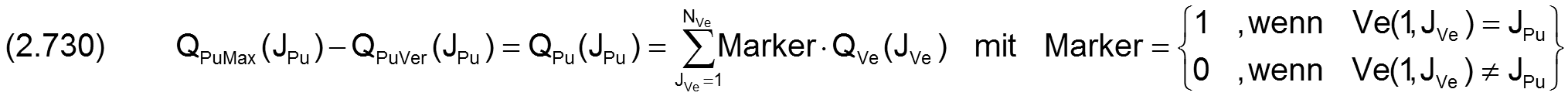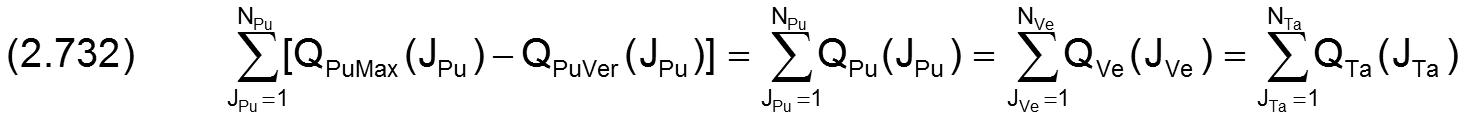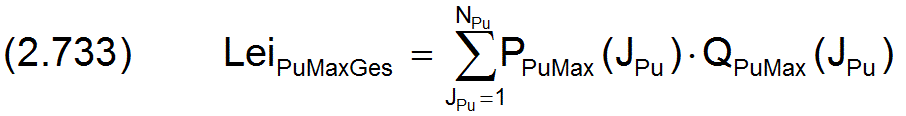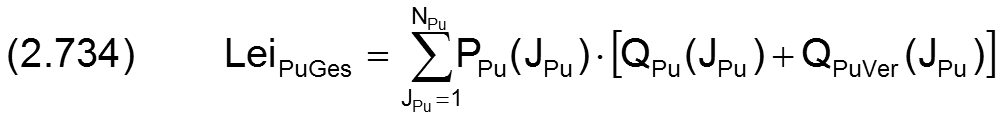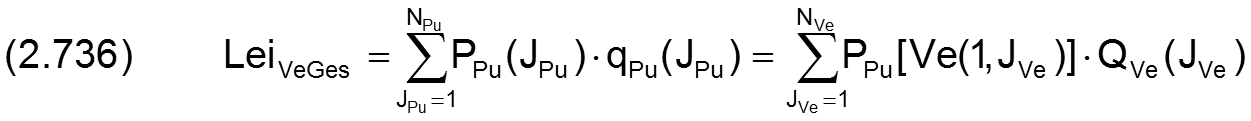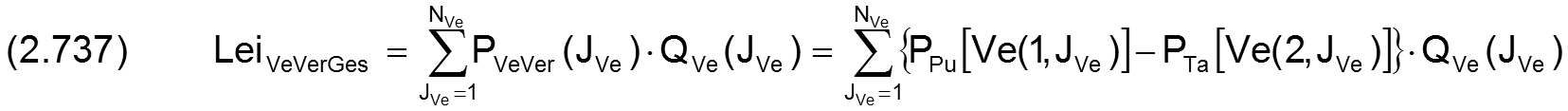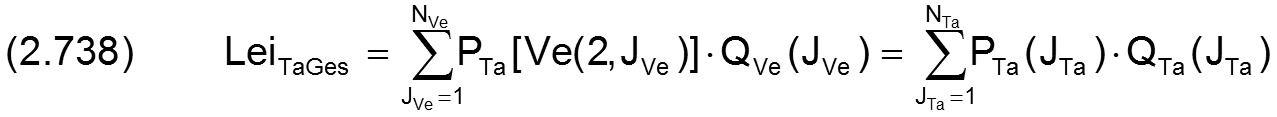zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.3 Hydrodynamische Schmiertheorie in dimensionsloser Form
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.3.1 Klassische hydrodynamische Theorie in dimensionsloser Form
Die Reynoldssche Differentialgleichung in dimensionsloser Form lautet
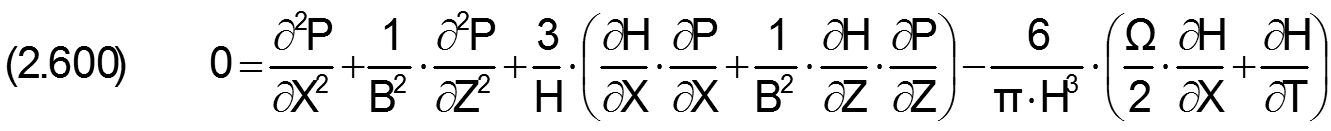
der dimensionslose Druck P im Schmierspalt und seine partiellen Ableitungen nach X und Z sind definiert durch
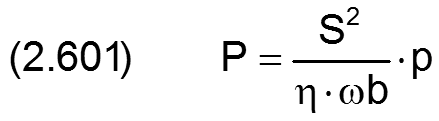
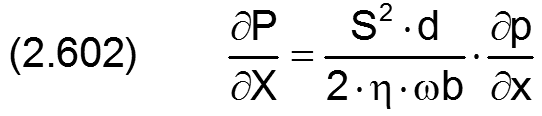
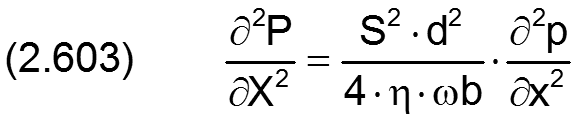

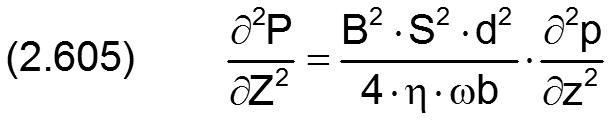
Die dimensionslose Wellendrehgeschwindigkeit Ω und die dimensionslose Zeit T sind definiert durch
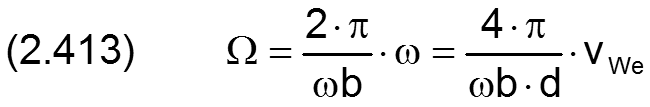
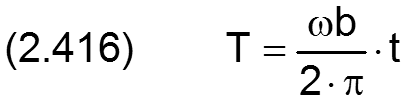
Bild 2.152 zeigt eine dimensionslose Druckverteilung P(X) nach der klassischen Reynoldsschen Differentialgleichung und der Annahme der "Gümbelschen Randbedingung" und die zugehörige dimensionslose Spalthöhe H(X) in Lagermitte über den Lagerumfang von X= -π bis +π bzw. -180° bis +180°.
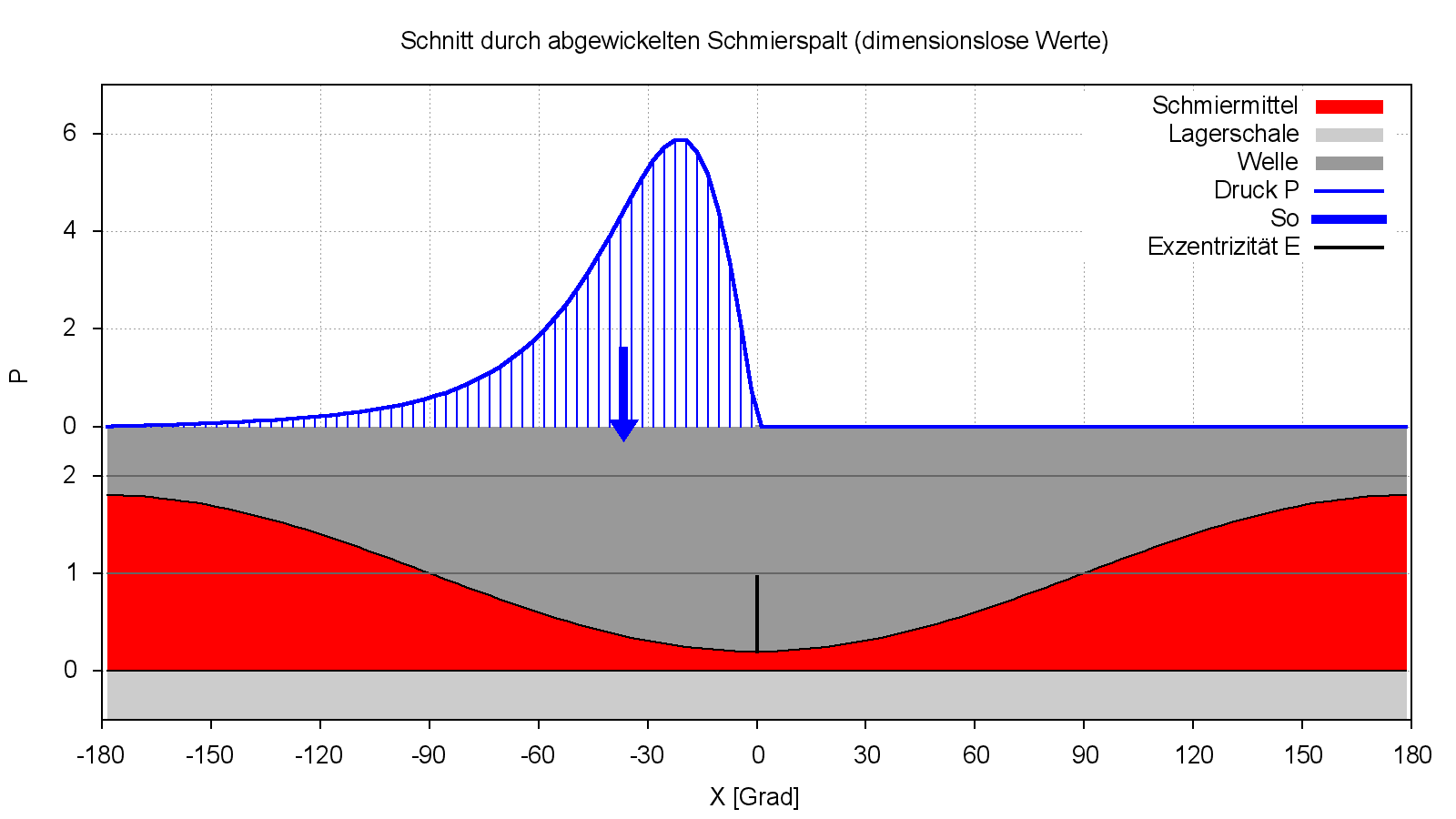
Bild 2.152: Druckverlauf P(X) und Spalthöhe H(X) in der Mitte eines stationär belasteten Lagers berechnet mit der klassischen Reynoldsschen Differentialgleichung und Annahme der "Gümbelschen Randbedingung"
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.3.2 Erweiterte hydrodynamische Theorie in dimensionsloser Form
Die dimensionslose erweiterte Reynoldssche Differentialgleichung lautet
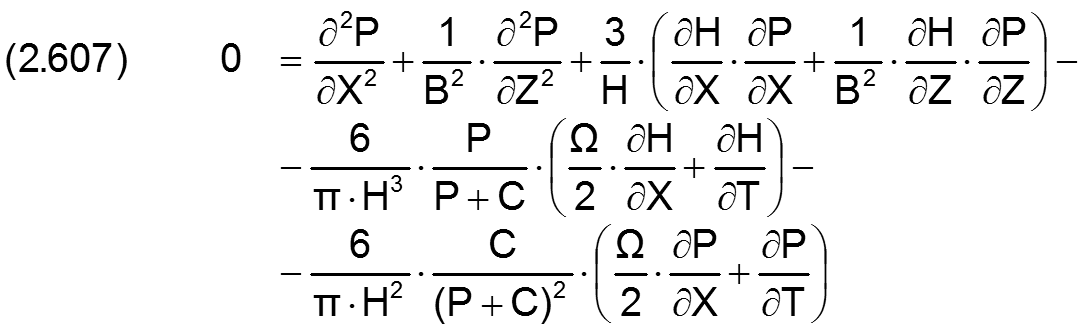
Die neu hinzukommenden dimensionslosen Parameter sind hier die dimensionslose Mischungskonstante C
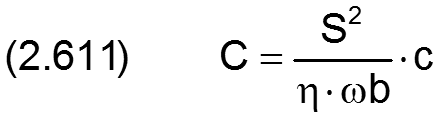
und die partielle Ableitung des Druckes P nach der dimensionslosen Zeit T
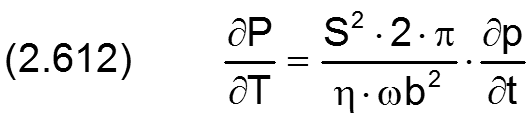
Der generell dimensionslose örtliche Füllungsgrad F kann auch aus dem dimensionslosen Druck P und der dimensionslosen Mischungskonstanten C berechnet werden durch
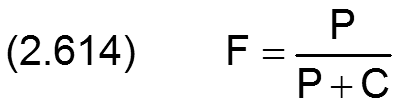
Bild 2.154 zeigt eine dimensionslose Druckverteilung P(X) in Lagermitte nach der erweiterten Reynoldsschen Differentialgleichung und die zugehörige dimensionslose Spalthöhe H(X) und darin die entsprechenden Anteile flüssiger Phase (rot) und gasförmiger Phase (gelb) über den Lagerumfang von X= -π bis +π bzw. -180° bis +180°.
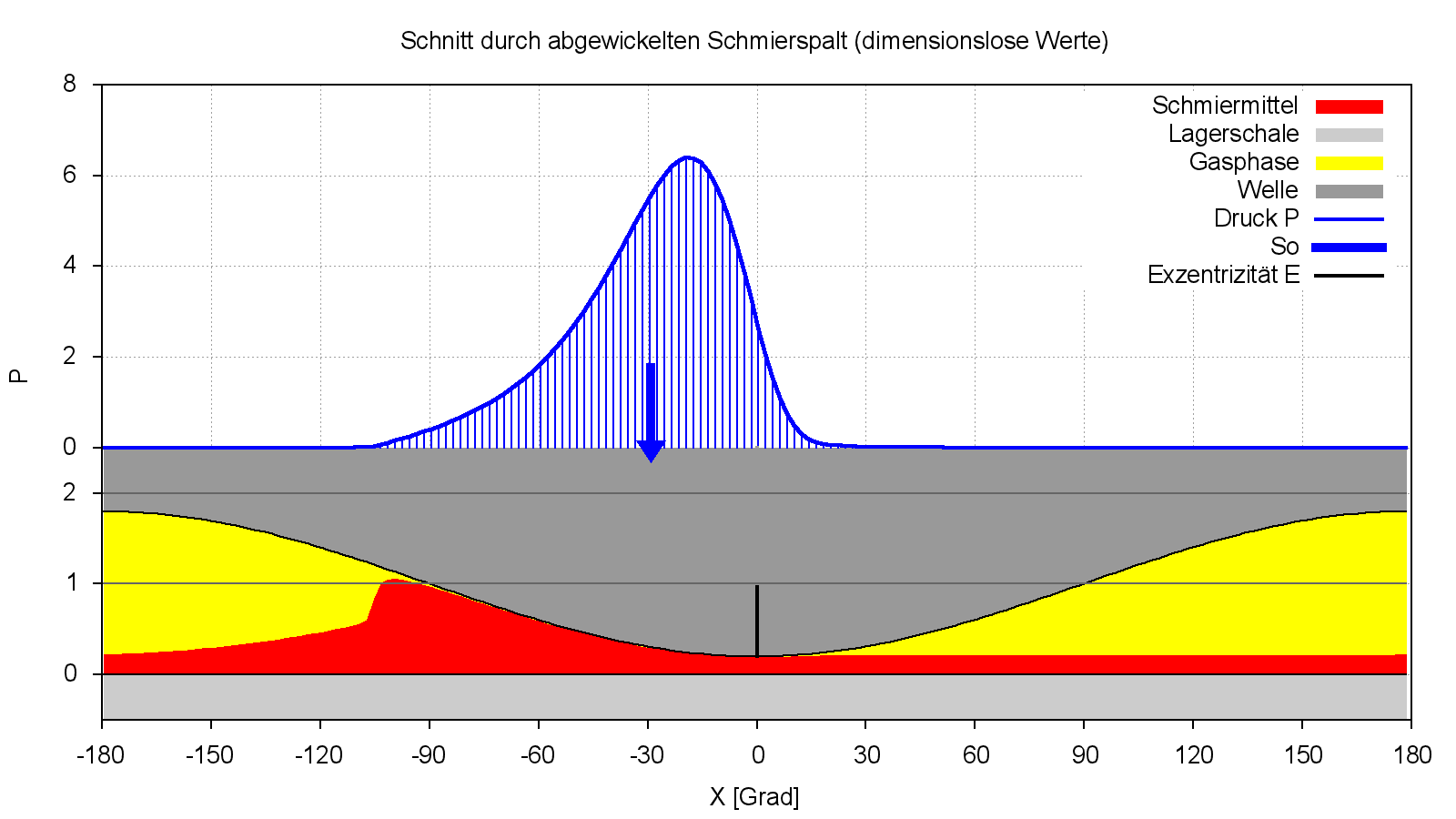
Bild 2.154: Druckverlauf P(X), Spalthöhe H(X) und Flüssigkeitsverteilung HF=H·F in der Mitte eines stationär belasteten Lagers berechnet mit der erweiterten Reynoldsschen Differentialgleichung
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.4 Dimensionslose Lagerbelastung
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.4.1 Dimensionslose Lagerkräfte
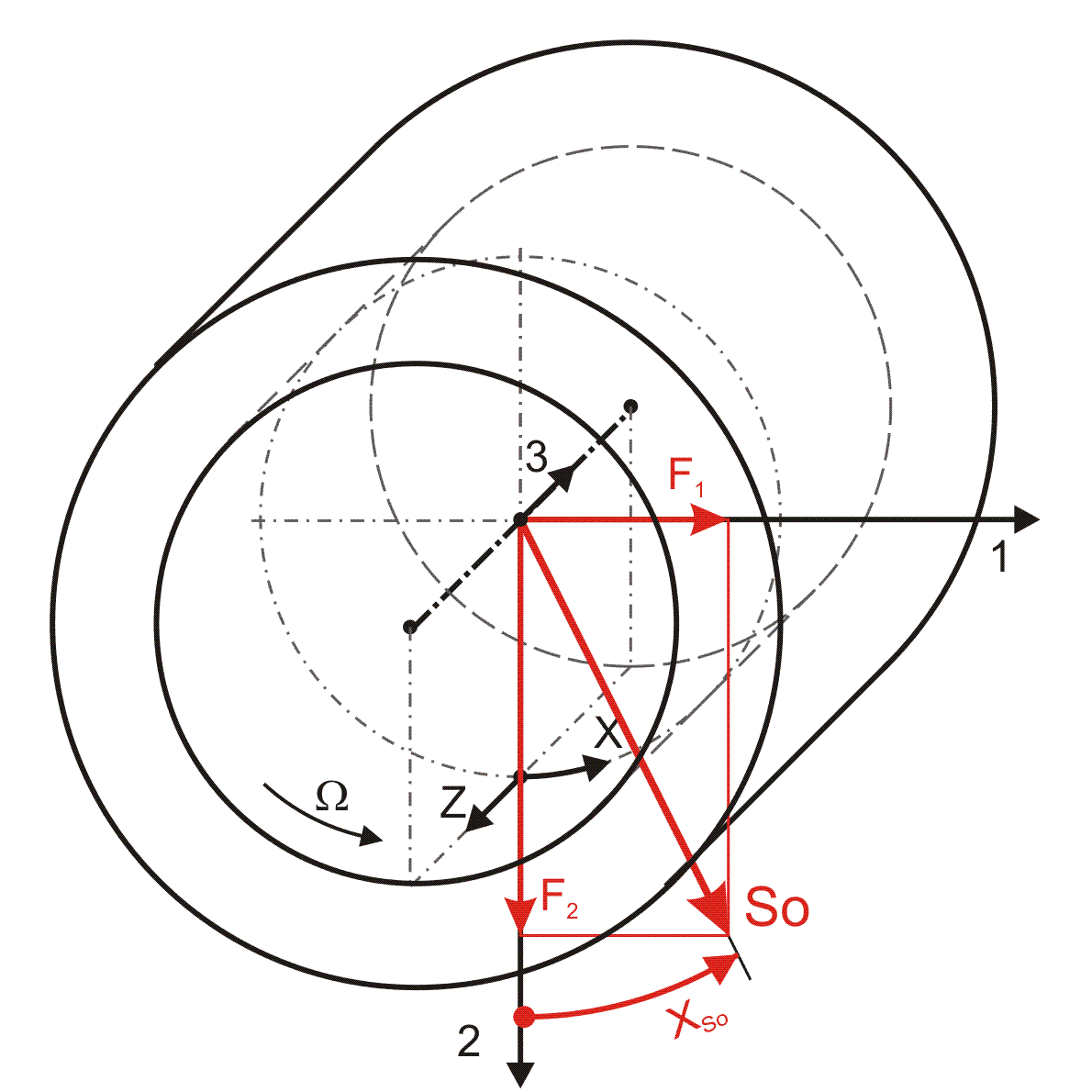
Bild 2.156: Dimensionslose Lagerkräfte
Die Lagerkräfte werden in folgender Weise dimensionslos gemacht:
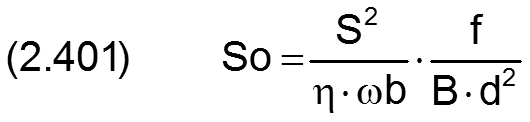
Der Betrag der dimensionslosen Lagerkraft ist die Sommerfeldzahl.
Die Komponenten F1 und F2 der dimensionslosen Lagerkraft werden analog dimensionslos gemacht
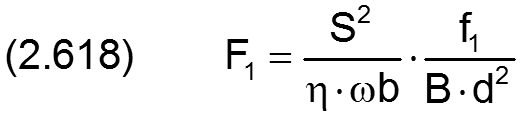
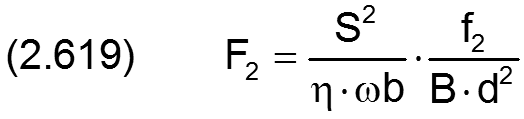
Die Komponenten F1 und F2 der dimensionslosen Lagerkraft werden berechnet durch die Integrale
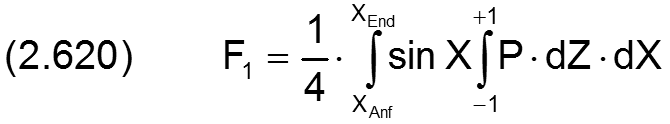
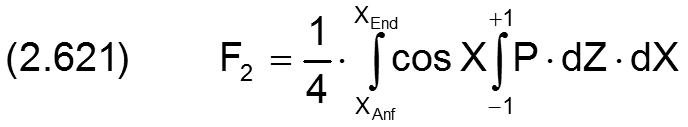
Der Betrag der resultierenden Lagerkraft So wird berechnet durch
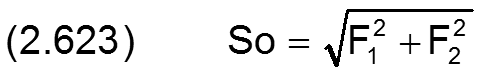
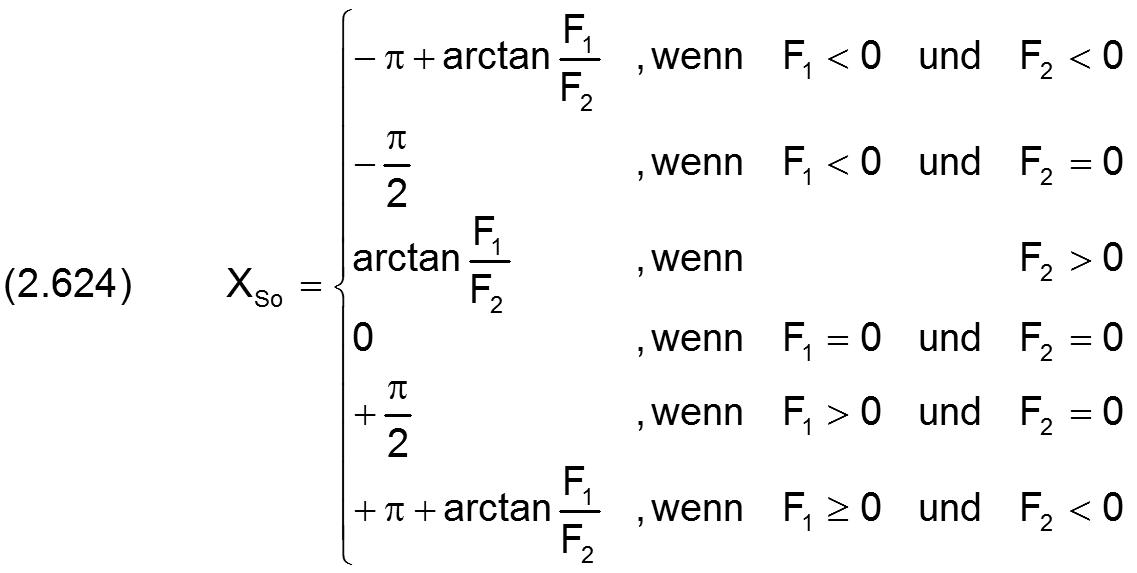
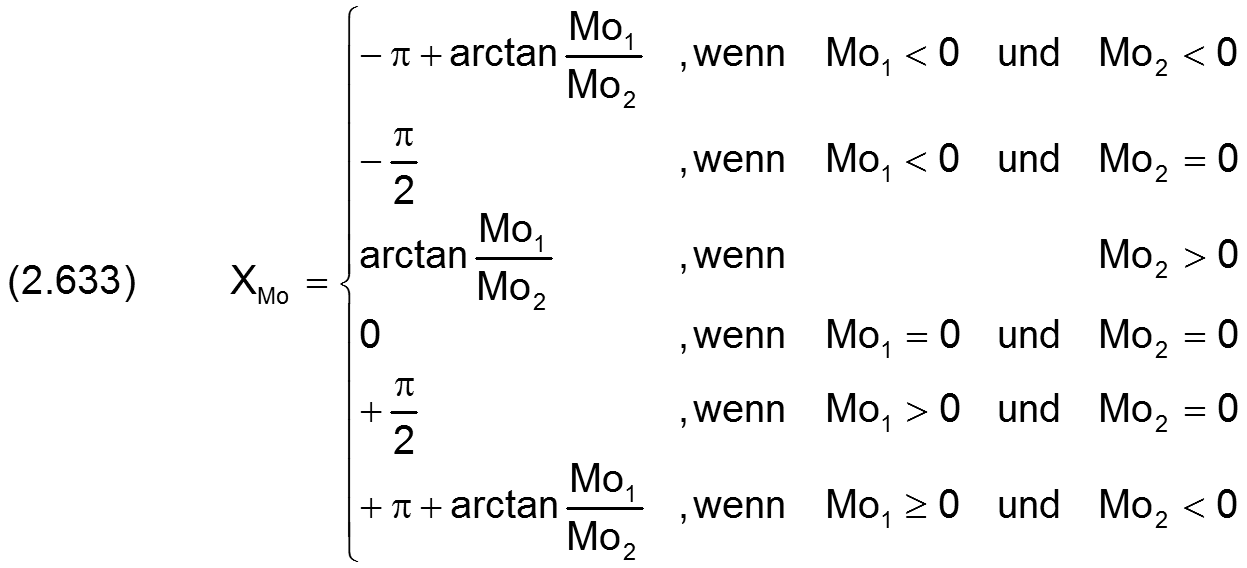
Die Richtung der resultierenden Kraft ist gegeben durch den Winkel XSo, mit
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.4.2 Instationäre dimensionslose Lagerkräfte
Die dimensionslose Lagerbelastung, gegeben durch die Parameter der Kraft So und der Kraftrichtung XSo bzw. durch die Komponenten der Lagerkraft F1 und F2, können als konstant oder als zeitlich variabel angenommen werden. Wenn die Verlagerungsbahn aus einem vorgegebenen (gemessenen) Verlauf der Lagerbelastung berechnet werden soll, dann können die entsprechenden Parameter der Lagerkraft für die zu berechnenden NT Zeitpunkte punktweise eingegeben werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lager, wenn noch keine konkreten Daten für den Kraftverlauf bekannt sind, können komplette Kraftverläufe auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung des Kraftverlaufs implementiert.

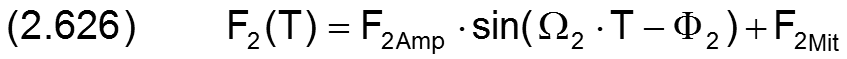
mit
| F1Amp |
Amplitude der Lagerkraft F1 |
| F1Mit |
Mittelwert der Lagerkraft F1 |
| Ω1 |
Phasenwinkelgeschwindigkeit der Lagerkraft F1 |
| Φ1 |
Phasenwinkel der Lagerkraft F1 zum Zeitpunkt T=0 |
| F2Amp |
Amplitude der Lagerkraft F2 |
| F2Mit |
Mittelwert der Lagerkraft F2 |
| Ω2 |
Phasenwinkelgeschwindigkeit der Lagerkraft F2 |
| Φ2 |
Phasenwinkel der Lagerkraft F2 zum Zeitpunkt T=0 |
Bild 2.157 zeigt ein Beispiel für einen dimensionslosen Kraftverlauf mit den Werten F1Amp = 0,076; F1Mit = 0; Ω1 = 2·π; Φ1 = -π/2; F2Amp = 0,955; F2Mit = 0,955; Ω2 = 2·π; Φ2 = 0; B=0,5.
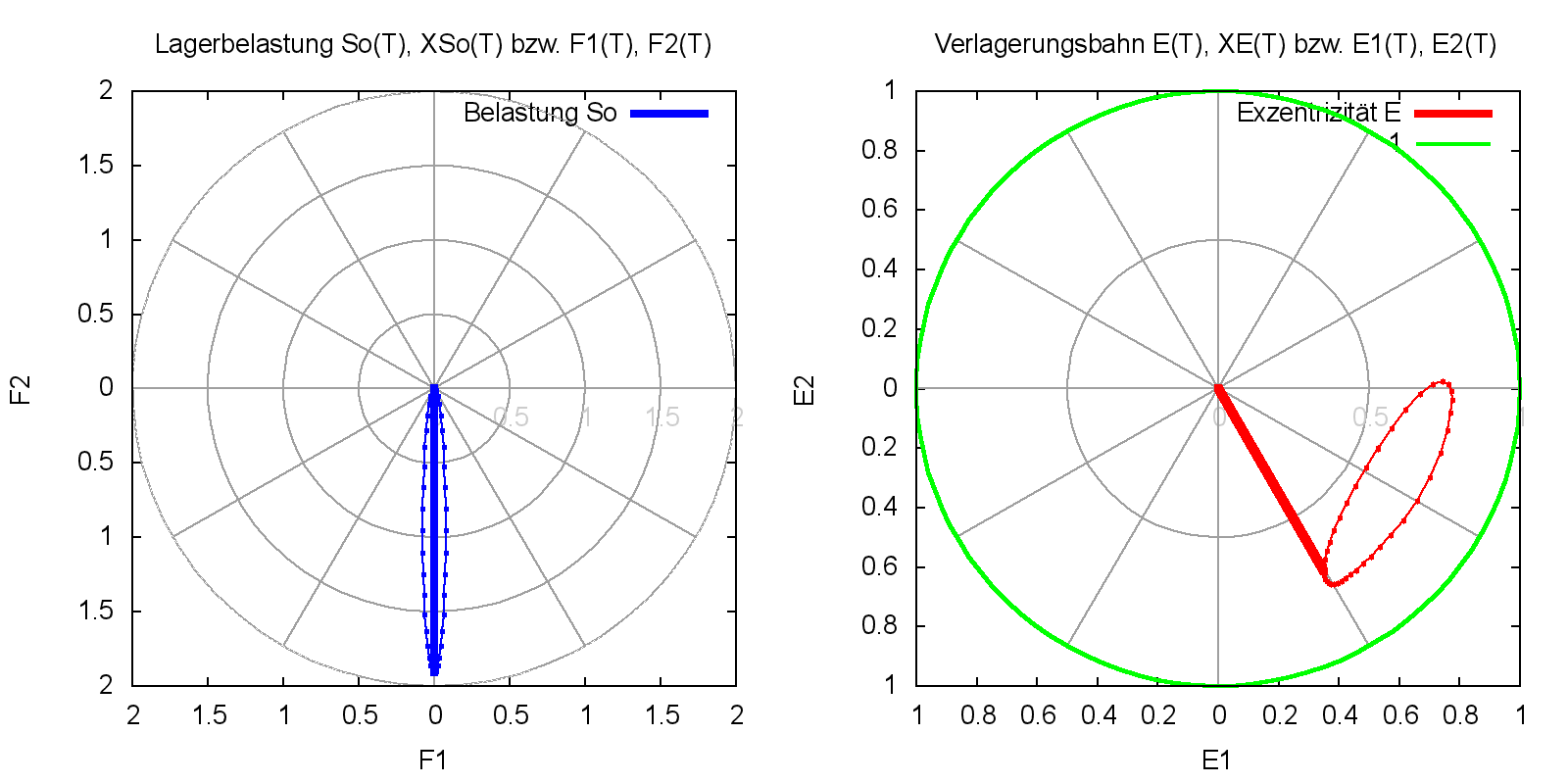
Bild 2.157: Beispiel für einen Kraftverlauf (links), der durch die Parameter einer Funktion vorgegeben wurde, und rechts die zugehörige Verlagerungsbahn (Animation)
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.4.3 Dimensionslose Kippmomente
Kippmomente am Lager entstehen bei asymmetrischer Spaltgeometrie, z.B. bei Verkantung der Welle in der Lagerschale.
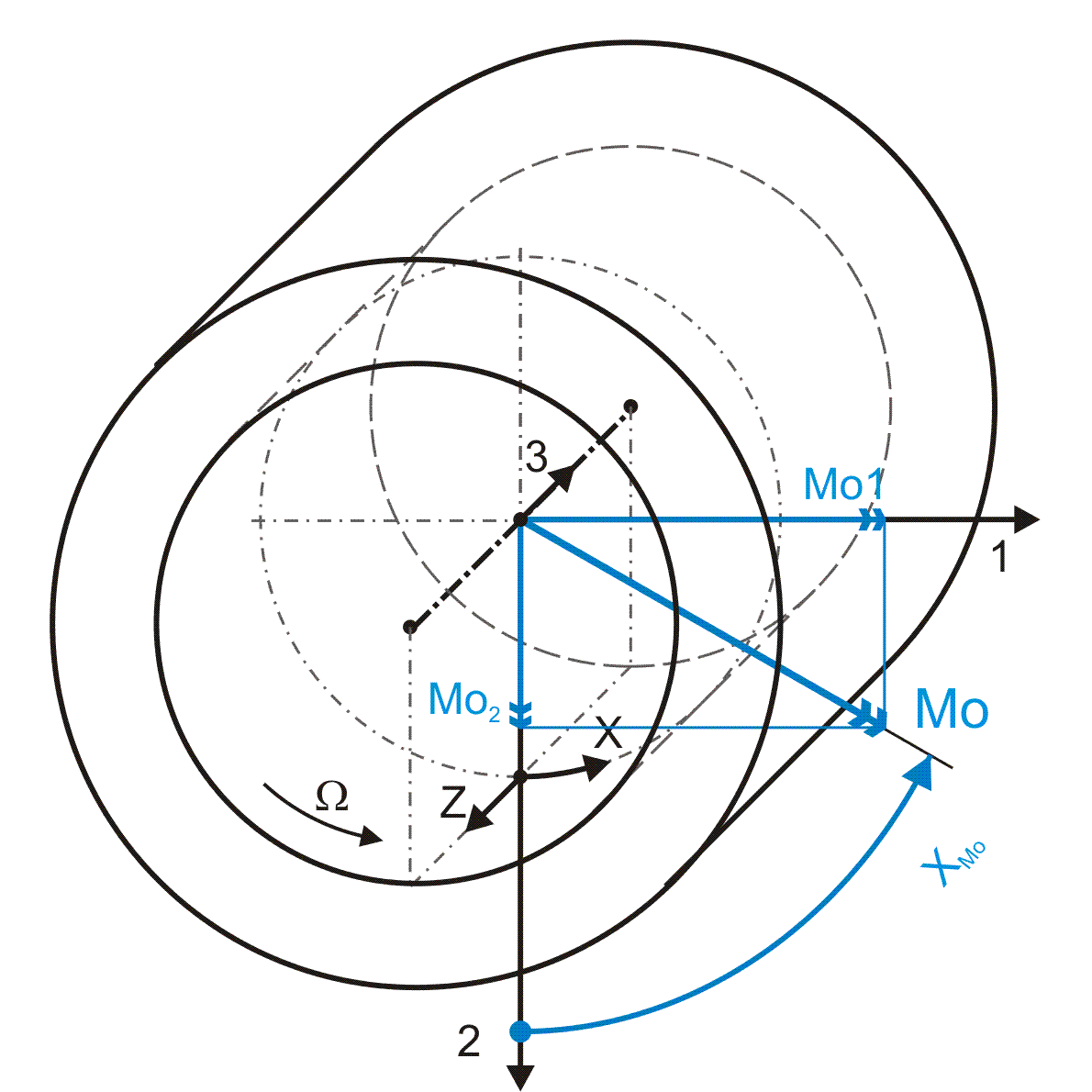
Bild 2.158: Dimensionslose Kippmomente
Der Betrag des dimensionslosen Kippmoments Mo ist definiert durch
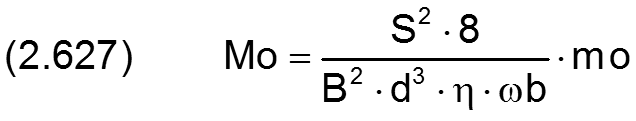
Entsprechend gilt für die horizontale Komponente Mo1
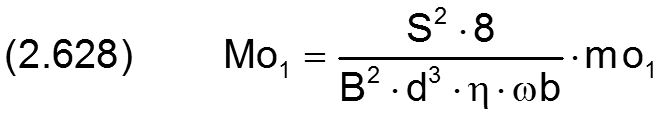
und für die vertikale Komponente Mo2
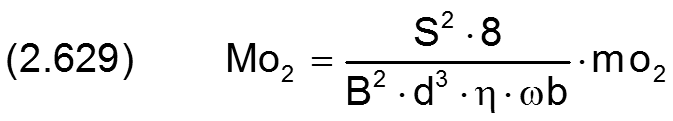
HINWEIS: Die Kippmomente Mo, Mo1 und Mo2 werden hier anders dimensionslos gemacht als das Reibmoment MoWe.
Die Komponenten Mo1 und Mo2 des dimensionslosen Kippmoments werden berechnet durch die Integrale

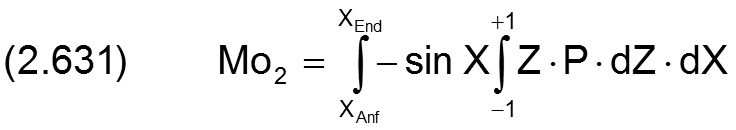
Der Betrag des resultierenden Kippmoments Mo wird berechnet durch

Die Richtung des resultierenden Kippmoments ist gegeben durch den Winkel XMo, mit
Die dritte mögliche Komponente MoWe eines Moments, welche in die axiale Richtung zeigt, gehört nicht zum Kippmoment. Es ist das Reibmoment und wird im Rahmen der Energiebilanz des Lagers berechnet. Siehe dazu folgenden Abschnitt 2.2.4.4.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.4.4 Wellenreibmoment MoWe und Wellenreibleistung LeiWe
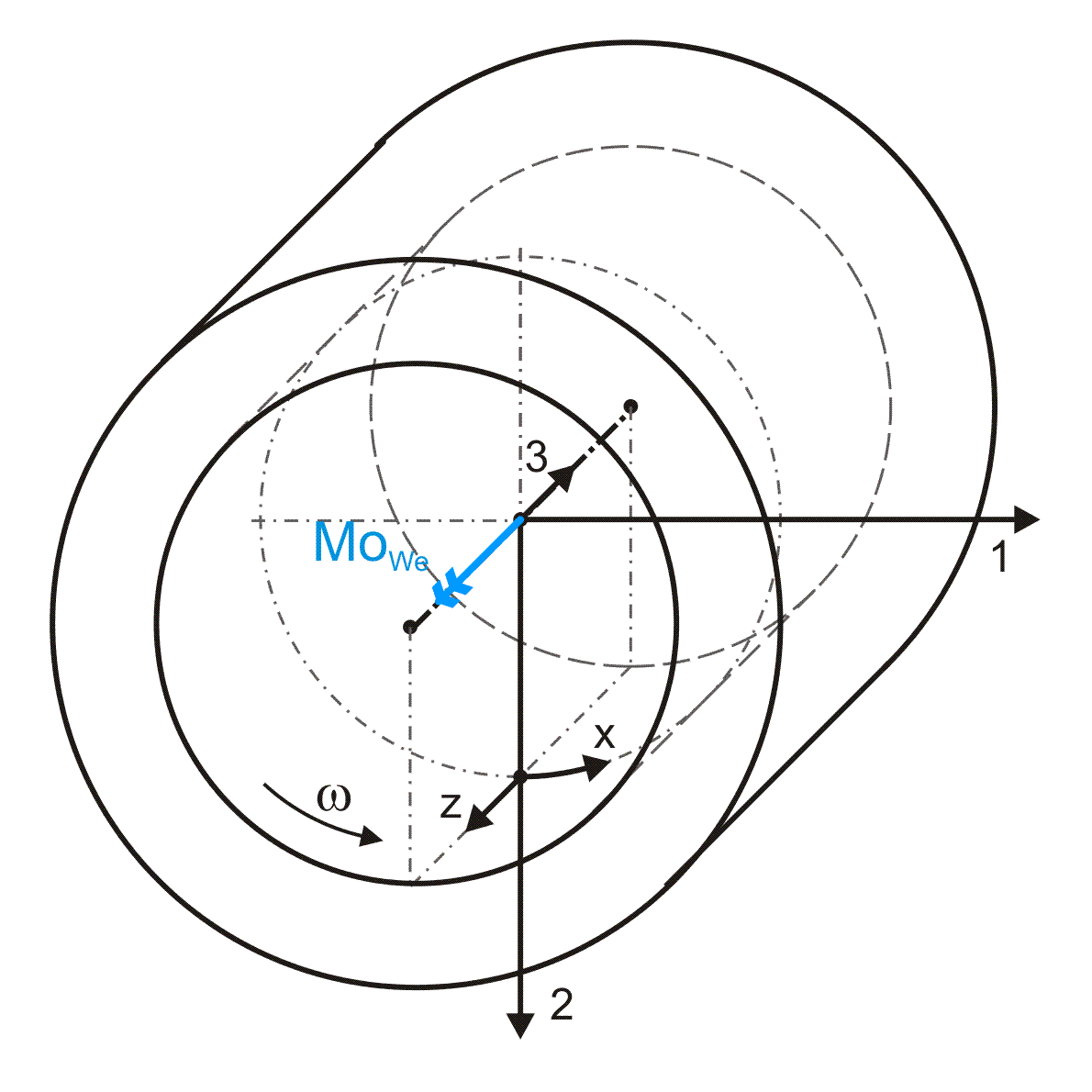
Bild 2.159: Dimensionsloses Reibmoment
Das Wellenreibmoment wird auf folgende Weise dimensionslos gemacht
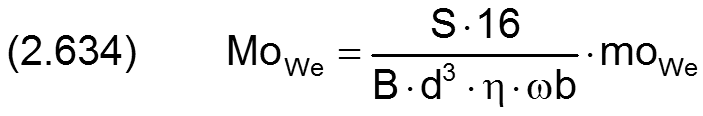
HINWEIS: Das Reibmoment MoWe wird hier anders dimensionslos gemacht als die Kippmomente Mo1 und Mo2.
Die Gleichung (2.235) für das Reibmoment moWe lässt sich mit den Gleichungen (2.404), (2.405), (2.423), (2.601), (2.602) und (2.634) in die dimensionslose Form bringen
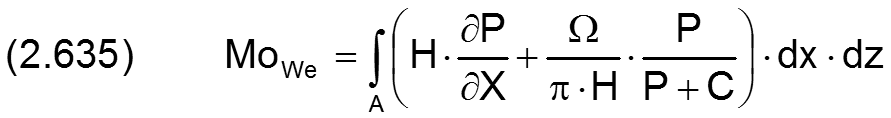
Hier ist die Fläche A=((XEnd-XAnf)·(ZEnd-ZAnf)-Taschenflächen), die gesamte Schmierspaltfläche unter Abzug aller Flächen der Schmiertaschen. Das ergibt sich aus der Annahme, dass die Schmiertaschentiefe viel größer ist als die Spalthöhen H(X,Z) und dass deshalb die innere Reibungen in den Schmiertaschen vernachlässigt wird.
Die Leistung allgemein wird auf folgende Weise dimensionslos gemacht
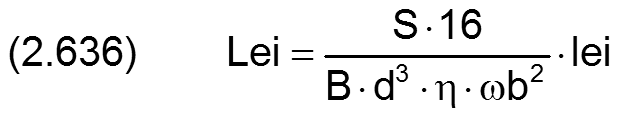
Die Gleichung (2.237) für die Reibleistung leiWe der Welle lässt sich mit den Gleichungen (2.413), (2.634) und (2.636) in die dimensionslose Form bringen
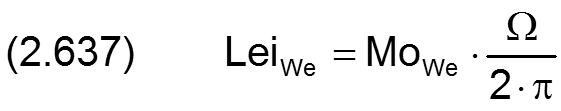
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5 Dimensionslose Bilanz der Flüssigkeits- und Energieströme des Schmierspalts
HINWEIS: Wenn nachfolgend von Flüssigkeits- oder Ölströmen die Rede ist, dann sind die Volumenanteile der flüssigen inkompressiblen Phase des Flüssigkeits-Gasgemischs im Schmierspalt gemeint und nicht der Gesamtvolumenstrom des Gemischs, das stets den gesamten Schmierspalt ausfüllt und gemäß den Annahmen der erweiterten Reynoldsschen Gleichung auch als eine homogene aber kompressible Flüssigkeit angesehen werden könnte.
HINWEIS: Nach der klassischen Reynoldsschen Gleichung wird angenommen, dass der Schmierspalt vollständig mit inkompressibler Flüssigkeit gefüllt ist. Deshalb braucht hier nicht auf den Unterschied zwischen Schmierspalt- und Flüssigkeitsvolumen geachtet werden. Die hier dargestellten Formeln können aber auch angewendet werden, wenn der örtliche Füllungsgrad F für den gesamten Schmierspalt auf 1 gesetzt wird. Dabei ist aber darauf hinzuweisen, dass für die Berechnung der Ölstrombilanz die klassische Reynoldssche Differentialgleichung meist unbefriedigende Ergebnisse liefert, weil sie die Kavitationsgebiete aus der Berechnung ausschließt und damit in diesem Gebiet gegen die Kontinuitätsbedingung verstößt.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.1 Strömungsgeschwindigkeiten im Schmierspalt
Für die Strömungsgeschwindigkeiten im Schmierspalt wurde keine dimensionslose Darstellung entwickelt, da diese Geschwindigkeiten im Programm nicht explizit vorkommen.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.2 Über die Lagerränder abfließender dimensionsloser Ölstrom QRand
Bild 2.162 zeigt den abgewickelten Schmierspalt eines teilweise umschlossenen Lagers mit seinen 4 Rändern und seinen dimensionslosen Ölströmen QRand1, QRand2, QRand3 und QRand4 über diese Ränder.
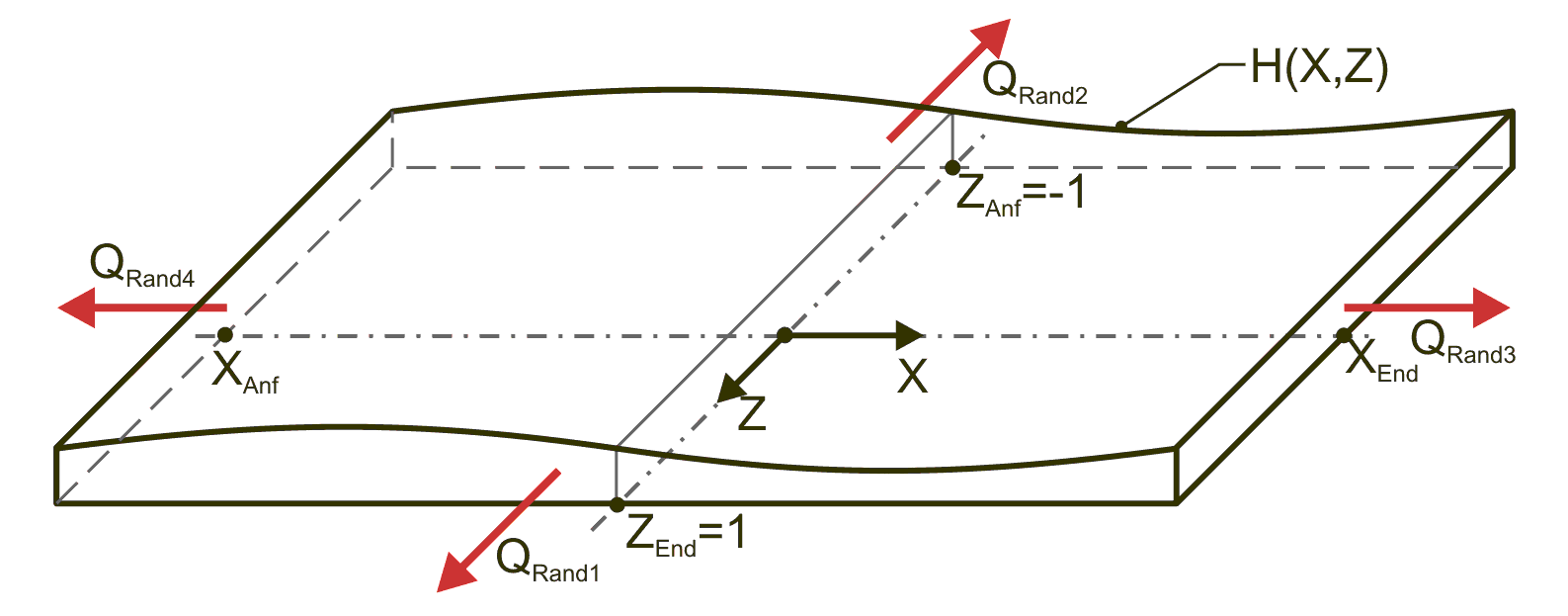
Bild 2.162: Abgewickelte dimensionslose Schmierspaltfläche mit den 4 möglichen Ölströmen über die Schmierspaltränder
Für ein teilweise umschlossenes Lager wird ein konstanter Umgebungsdruck PRand1 für den gesamten Lagerrand angenommen und es ergibt sich durch Einsetzen von PRand1 in Gleichung (2.614)
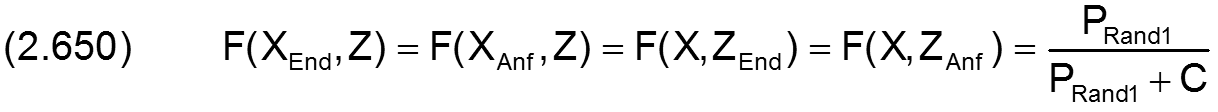 |
für X = XAnf bis XEnd und Z = -1 bis +1 |
Volumenströme werden in folgender Weise dimensionslos gemacht
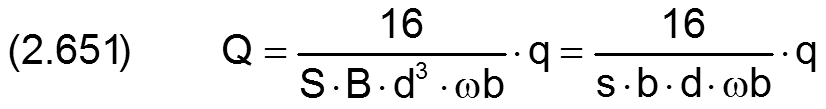
Durch Einführung der dimensionslosen Parameter gemäß den Gleichungen (2.404), (2.405), (2.413), (2.601), (2.602), (2.604) und (2.651) in die Gleichungen (2.252), (2.253), (2.254) und (2.255) ergeben sich die folgenden Gleichungen für die dimensionslosen Ölströme QRand1 bis QRand4
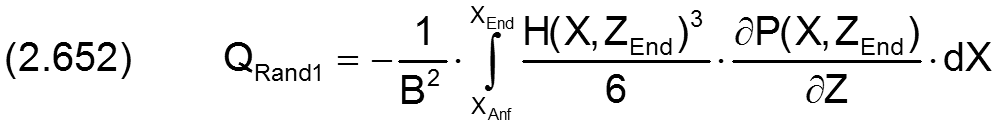

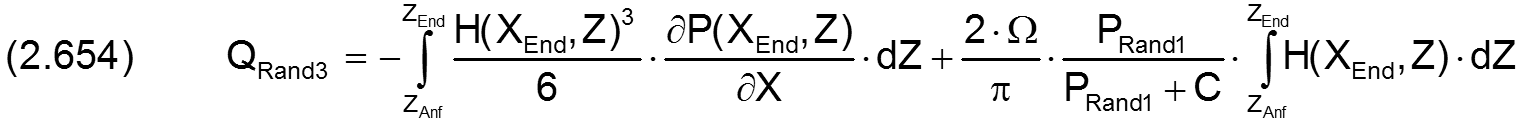
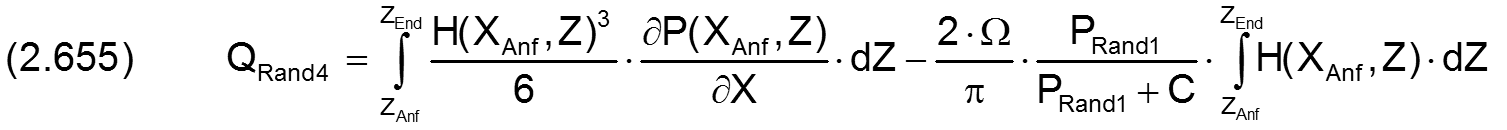
und der dimensionslose Gesamtölstrom QRand

Das voll umschlossene Lager hat nur die zwei Ränder bei Z=ZAnf und Z=ZEnd. Damit ergibt sich hier für das voll umschlossene Lager ein Gesamtölstrom von
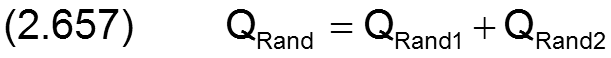
Wenn das voll umschlossene Lager außerdem symmetrisch ist gilt
 zurück
weiter
zur dimensionsbehafteten Darstellung
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.3 Dimensionsloser Ölstrom QTaRand von einer Schmiertasche über den Taschenrand in den Schmierspalt
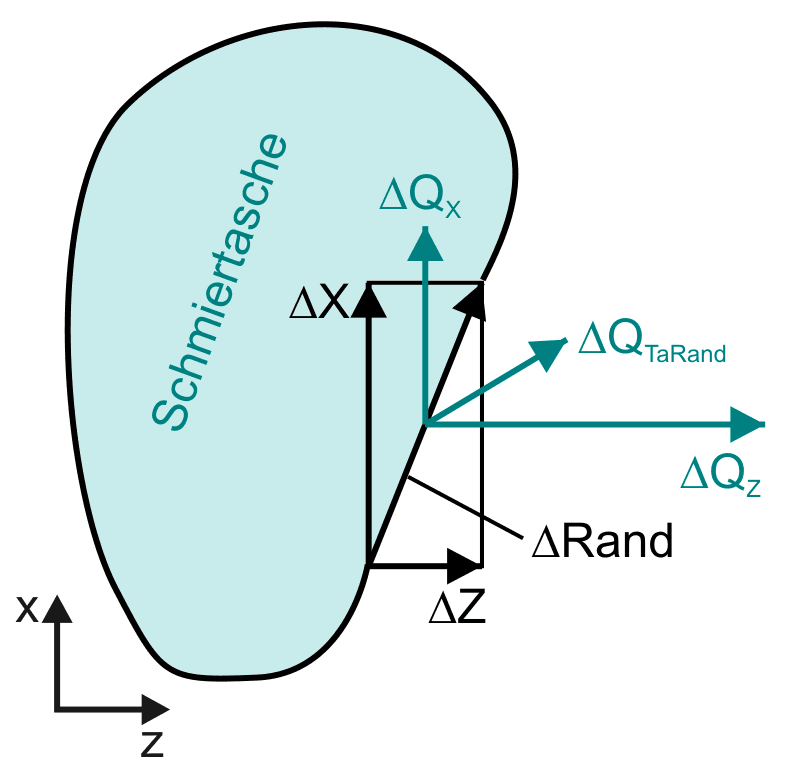
Bild 2.163: Dimensionsloser Ölstrom ΔQTaRand über das Randelement ΔRand aus einer Schmiertasche in den Schmierspalt
Bild 2.163 zeigt die Randkontur einer Schmiertasche mit einem gerichteten Randstück ΔRand und skizziert den dimensionslosen Ölstrom ΔQTaRand über das Randelement Rand aus der Schmiertasche in den eigentlichen Schmierspalt. Der resultierende Ölstrom ΔQTaRand ist dann die Summe

Die Gleichung (2.267) für den dimensionsbehafteten Ölstrom qTaRand über den Rand einer Schmiertasche lässt sich mit den Gleichungen (2.404), (2.405), (2.423), (2.601), (2.602), (2.604) und (2.651) in die dimensionslose Form bringen
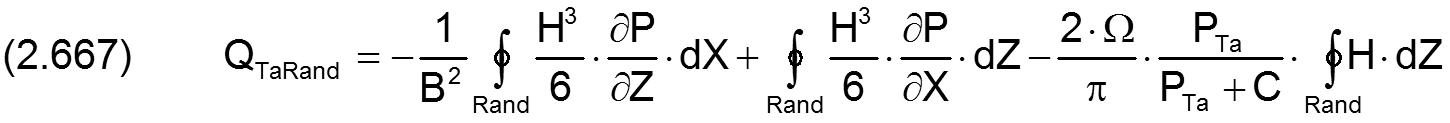
HINWEIS: Zu beachten ist bei dieser Gleichung, dass von der Drehrichtung, mit der die Integration über den Rand ausgeführt wird, das Vorzeichen des berechneten Ölstroms abhängt. Hier soll ein Ölstrom aus der Schmiertasche in den Schmierspalt ein positives Vorzeichen bekommen. Das ist der Fall, wenn das Ringintegral rechtsdrehend (entgegen dem Uhrzeiger) um die Fläche der Schmiertasche herum ausgeführt wird.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.4 Dimensionslose Volumenänderung ∂VolFlTa/∂T der Schmierflüssigkeit in einer Schmiertasche über die Zeit
Eine Volumenänderung über die Zeit hat die gleiche Dimension wie ein Volumenstrom und wird deshalb in gleicher Weise dimensionslos gemacht mit

Für die erweiterte hydrodynamische Schmiertheorie ist die dimensionslose Volumenänderung einer Schmiertasche aus Gleichung (2.274) abgeleitet gegeben durch

Hier ist A die Fläche der Schmiertasche.
Für die klassische Schmiertheorie, bei der immer ein vollständig gefüllter Schmierspalt F=1 angenommen wird, vereinfacht sich die Gleichung zu
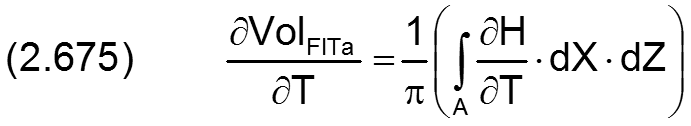
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.5 Dimensionslose Volumenbilanz der Schmiertaschen
Wenn in einem Lager NTa Schmiertaschen existieren, ist für jede dieser Taschen die Volumenbilanz der Schmierflüssigkeit aufzustellen durch die NTa Gleichungen
 |
für JTa = 1 bis NTa |
Dabei ist QTa(JTa) der dimensionslose Ölstrom der über eine Leitung vom Schmiermittelversorgungssystem des Lagers in die Schmiertasche Nr. JTa fließt, QTaRand(JTa) ist der Ölstrom der aus der Schmiertasche in den Schmierspalt weiter fließt und ∂VolFlTa(JTa)/∂T ist die Änderung des Flüssigkeitsvolumens in der Schmiertasche pro Zeit. Die Ölströme QTa(JTa) ergeben sich im Zusammenspiel mit dem peripheren Schmiermittel-Versorgungssystem und werden im Programm SIRIUS als primäre Ergebnisparameter mit berechnet und ausgegeben.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.6 Dimensionsloses Volumen der Flüssigkeit im Schmierspalt
Genau so, wie das Schmierspaltvolumen volSpalt (2.597) wird das Flüssigkeitsvolumen volFlSpalt im Schmierspalt dimensionslos gemacht
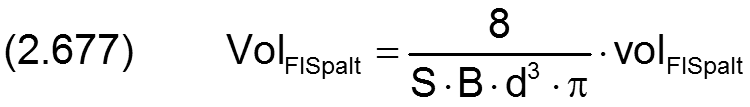
Durch Einführung der dimensionslosen Parameter gemäß den Gleichungen (2.404), (2.405), (2.423) und (2.677) in die Gleichung (2.278) ergibt sich die folgende Gleichung für die dimensionslosen Flüssigkeitsmenge VolFlSpalt im Schmierspalt

Der Gesamtfüllungsgrad FGes des Schmierspalts kann dann analog Gleichung (2.279) auch aus den entsprechenden dimensionslosen Werten berechnet werden durch

zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.7 Dimensionslose Strombilanz des gesamten Schmierspalts
Die Summe der zu- und abfließenden Flüssigkeitsströme ist gleich der Änderung des Flüssigkeitsvolumens im Schmierspalt. Analog zu den Gleichungen (2.280) und (2.281) lassen sich die Bilanzgleichungen für die dimensionslosen Ölströme aufstellen. Für ein teilweise umschlossenes Lager gilt
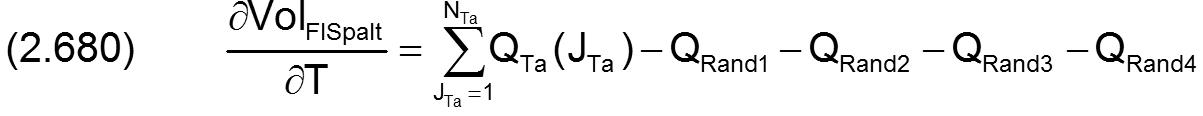
Für das voll umschlossene Lager gilt
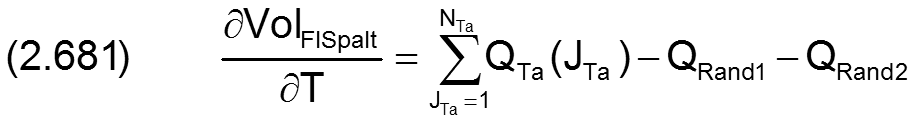
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.8 Dimensionslose innere Reibung im Schmierspalt
Die Gleichung (2.285) für die Leistung leiReib der inneren Reibung im Schmierfilm lässt sich mit den Gleichungen (2.636), (2.404), (2.405), (2.413), (2.423) und (2.601) in die dimensionslose Form bringen
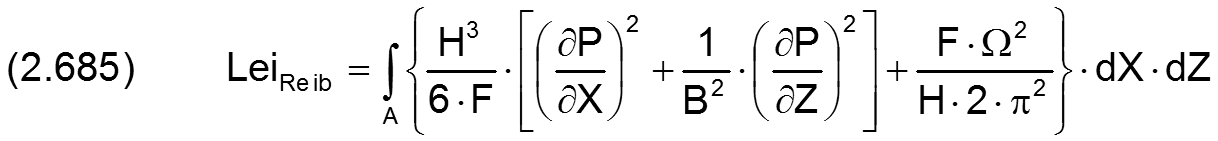
HINWEIS: Hier ist die Fläche A=((XEnd-XAnf)·(ZEnd-ZAnf)-Taschenflächen), die gesamte Schmierspaltfläche unter Abzug aller Flächen der Schmiertaschen. Das ergibt sich aus der Annahme, dass die Schmiertaschentiefe viel größer ist als die Spalthöhen H(X,Z) und deshalb innere Reibungen in den Schmiertaschen vernachlässigt wird.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.5.9 Dimensionslose Energiebilanz am Schmierspalt
Für den Schmierspalt des teilweise umschlossenen Lagers lässt sich die Energiebilanz analog Gleichung (2.286) aufstellen
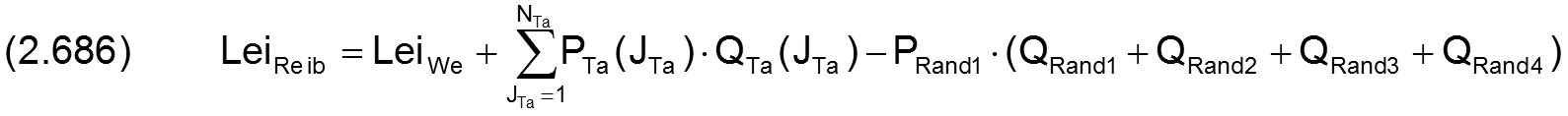
Für ein voll umschlossenes Lager gilt
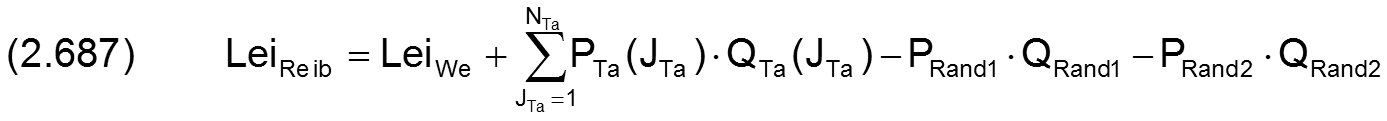
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6 Das dimensionslose periphere Schmiersystem
Allgemeine Erläuterungen siehe Abschnitt 2.1.6
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6.1 Schmiermittelpumpen in dimensionsloser Form
Die dimensionslose Pumpenkennlinie zeigt Bild 2.171
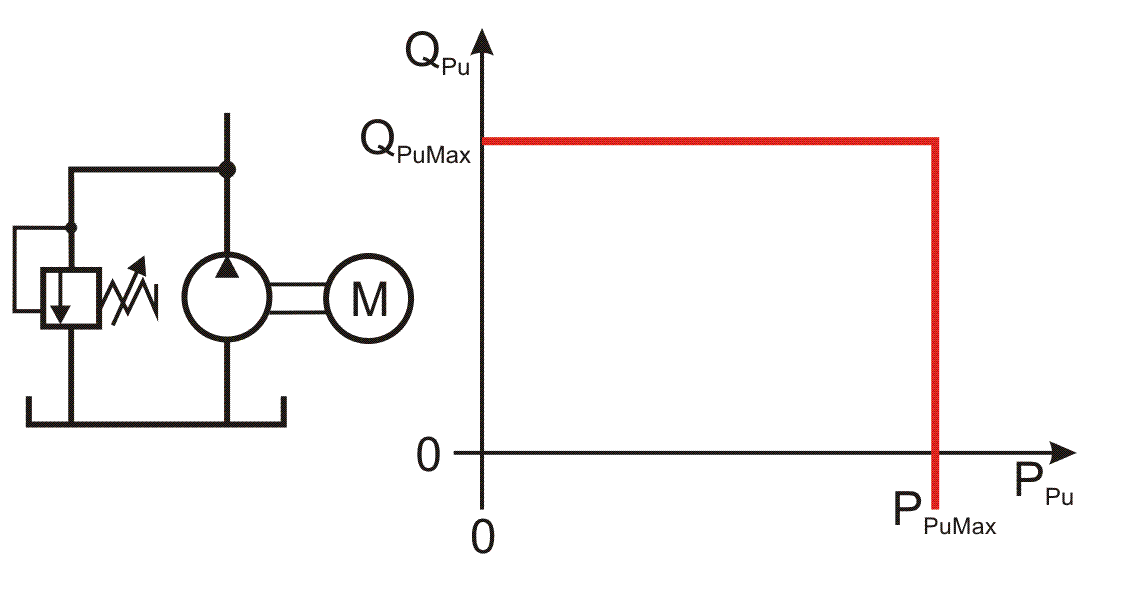
Bild 2.171: Betriebskennlinie einer Schmiermittelpumpe
Gemäß Gleichung (2.601) lassen sich die Pumpendrücke umrechnen
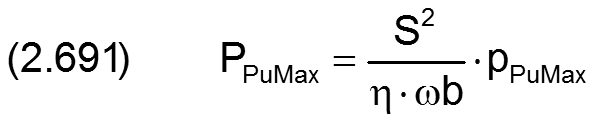
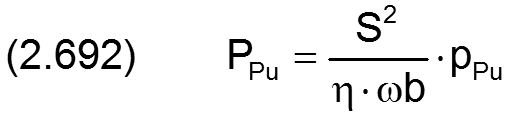
Gemäß Gleichung (2.651) lassen sich die Ölströme der Pumpen umrechnen

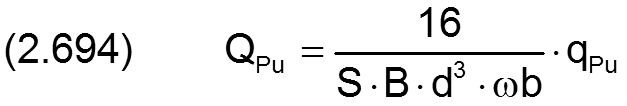
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6.2 Geräte in den Verbindungsleitungen zur Steuerung bzw. Regelung der Schmiermittelverteilung in die einzelnen Schmiertaschen in dimensionsloser Form
Nachfolgend werden die Gerätetypen beschrieben, die in den Verbindungsleitungen angeordnet werden können.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6.2.1 Laminardrossel bzw. Leitungswiderstand der Verbindungsleitung in dimensionsloser Form

Bild 2.173: Betriebskennlinie einer Laminardrossel, ohne Rückschlagventil links, mit Rückschlagventil rechts
Bild 2.173 zeigt die Kennlinien einer Laminardrossel mit und ohne Rückschlagventil. Es wird der dimensionslose Ölstrom QVe durch die Verbindungsleitung in Abhängigkeit vom dimensionslosen Schmiertaschendruck PTa dargestellt bei einem vorgegebenen Pumpendruck PPu.
Die Gleichung (2.295) für den Ölstrom durch die Kapillare lässt sich mit den Gleichungen (2.601), (2.651) und (2.697) in die dimensionslose Form bringen
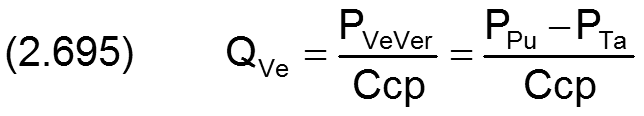
Der Strömungswiderstand rcp für den Widerstand einer Laminardrossel wird speziell für die Verwendung im Programm SIRIUS in einen dimensionslosen Widerstand Rcp umgerechnet durch
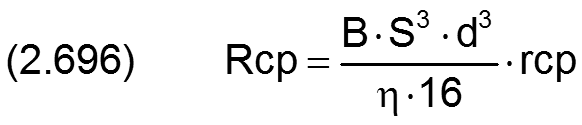
Der Widerstandsbeiwert ccp einer Kapillare kann auf ähnliche Weise dimensionslos gemacht werden durch
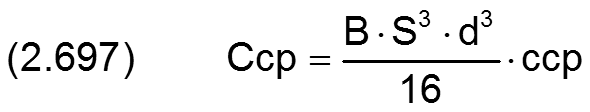
HINWEIS: Beachte, dass hier der Durchmesser d nicht etwa der Innendurchmesser der Kapillare ist, sondern der Wellendurchmesser des zu untersuchenden Lagers wie auch die anderen Bezugsparameter B, S und η.
Aus den Gleichungen (2.298), (2.696) und (2.697) ergibt sich interessanter Weise, dass der dimensionslose Widerstand Rcp einer Kapillare und der dimensionslose Widerstandsbeiwert Ccp identisch sind

HINWEIS: Im Programm SIRIUS wird mit dem Widerstandsbeiwert gearbeitet, weil dieser Wert auch im dimensionsbehafteten Zustand unabhängig von der Viskosität ist und damit ein konstanter Wert für verschiedene Betriebszustände.
Die Gleichung (2.300) für die Verlustleistung leiVeVer in der Kapillare einer Verbindungsleitung lässt sich mit den Gleichungen (2.601), (2.636), (2.651) und (2.697) in die dimensionslose Form bringen
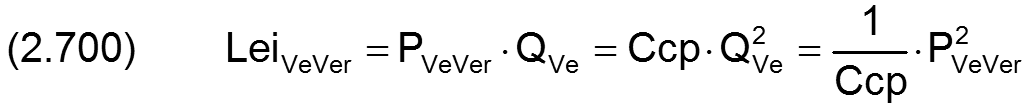
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6.2.2 Kombinierte Spalt- und Laminardrossel in dimensionsloser Form
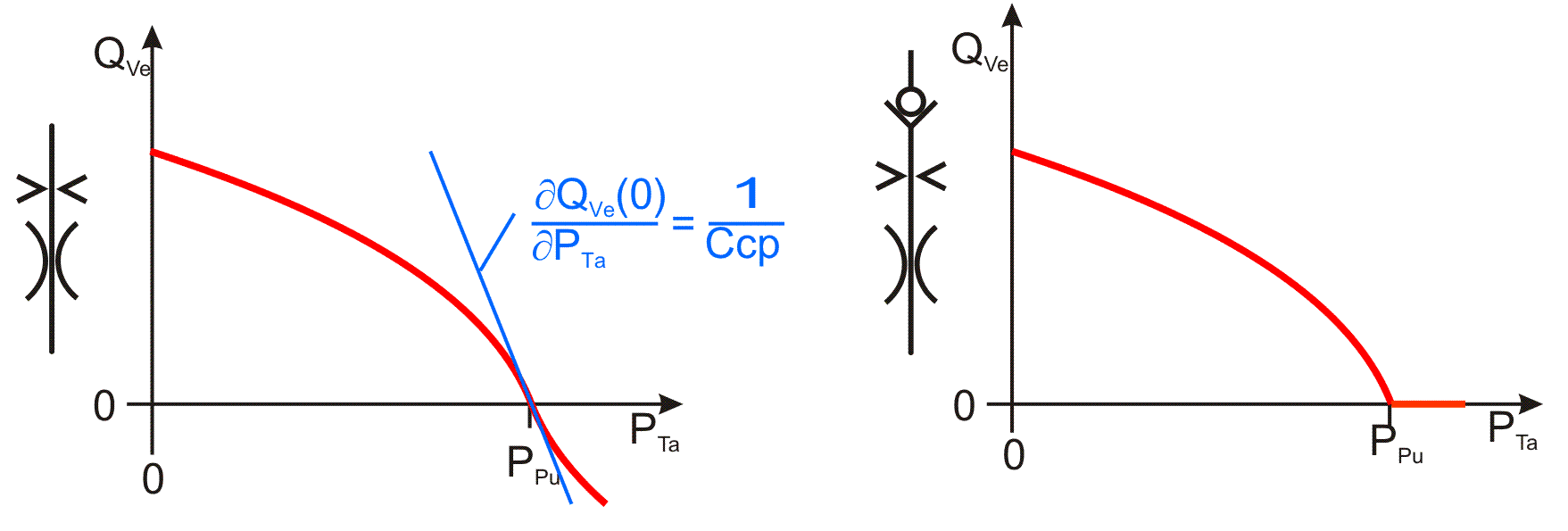
Bild 2.175: Betriebskennlinie einer Spaltdrossel in Reihe mit einer Laminardrossel, ohne Rückschlagventil links, mit Rückschlagventil rechts
Bild 2.175 zeigt die Kennlinien der Reihenschaltung einer Spaltdrossel mit einer Laminardrossel mit und ohne Rückschlagventil. Es wird der dimensionslose Ölstrom QVe durch die Verbindungsleitung in Abhängigkeit vom dimensionslosen Schmiertaschendruck PTa dargestellt bei einem vorgegebenen Pumpendruck PPu.
Die Gleichung (2.303) für den Ölstrom durch die reine Spaltdrossel lässt sich mit den Gleichungen (2.601), (2.651) und (2.704) in die dimensionslose Form bringen
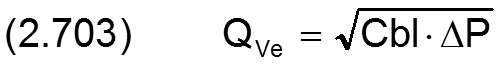
Der Blendenbeiwert cbl einer Spaltdrossel (Blende) wird hier dimensionslos gemacht durch
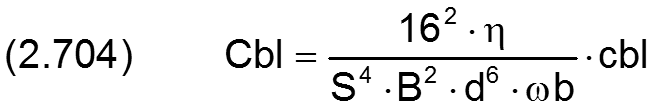
HINWEIS: Beachte, dass hier der Durchmesser d nicht etwa der lichte Durchmesser der Blende ist, sondern der Wellendurchmesser des zu untersuchenden Lagers wie auch die anderen Bezugsparameter B, S, η und ωb.
Im Programm wird die Blende nur in Kombination mit einer in Reihe geschalteten Laminardrossel modelliert. Die Kombination der Gleichungen (2.695) für die Laminardrossel und (2.703) für die Blende ergibt eine Strom-Druck-Kennlinie für eine Reihenschaltung von Laminardrossel und Spaltdrossel von
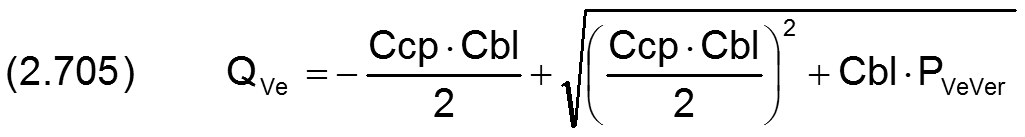 für PVeVer&gr;0
für PVeVer&gr;0
mit
| Ccp |
dimensionsloser Widerstandsbeiwert des laminaren Strömungswiderstandes |
| Cbl |
dimensionsloser Blendenbeiwert der Spaltdrossel |
| PVeVer |
dimensionsloser Druckverlust über die Drosseln PVeVer=PPu-PTa |
Wenn kein Rückschlagventil in der Schmiermittelleitung einen Rückstrom des Schmiermittels verhindert, gilt für den entsprechenden Rückfluss des Schmiermittels
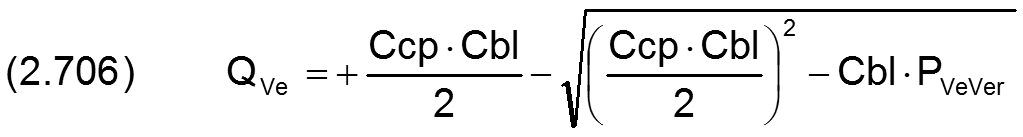 für PVeVer<0
für PVeVer<0
Dabei wird vereinfachend angenommen, dass die Drosselwirkung der Spaltdrossel in beiden Stromrichtungen gleich ist.
Die Gleichung (2.307) für die Verlustleistung leiVeVer in der Kapillare einer Verbindungsleitung lässt sich mit den Gleichungen (2.601), (2.636) und (2.651) in die dimensionslose Form bringen

zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6.2.3 PM-Regler mit idealisierter Kennlinie in dimensionsloser Form
Bild 2.180 zeigt links den prinzipiellen Aufbau eines PM-Reglers, in der Mitte ein vereinfachtes Schaltsymbol des Reglers und rechts die Standardkennlinie des Reglers und eine auf die Betriebsbedingungen umgerechnete Kennlinie, beide in dimensionsloser Form.
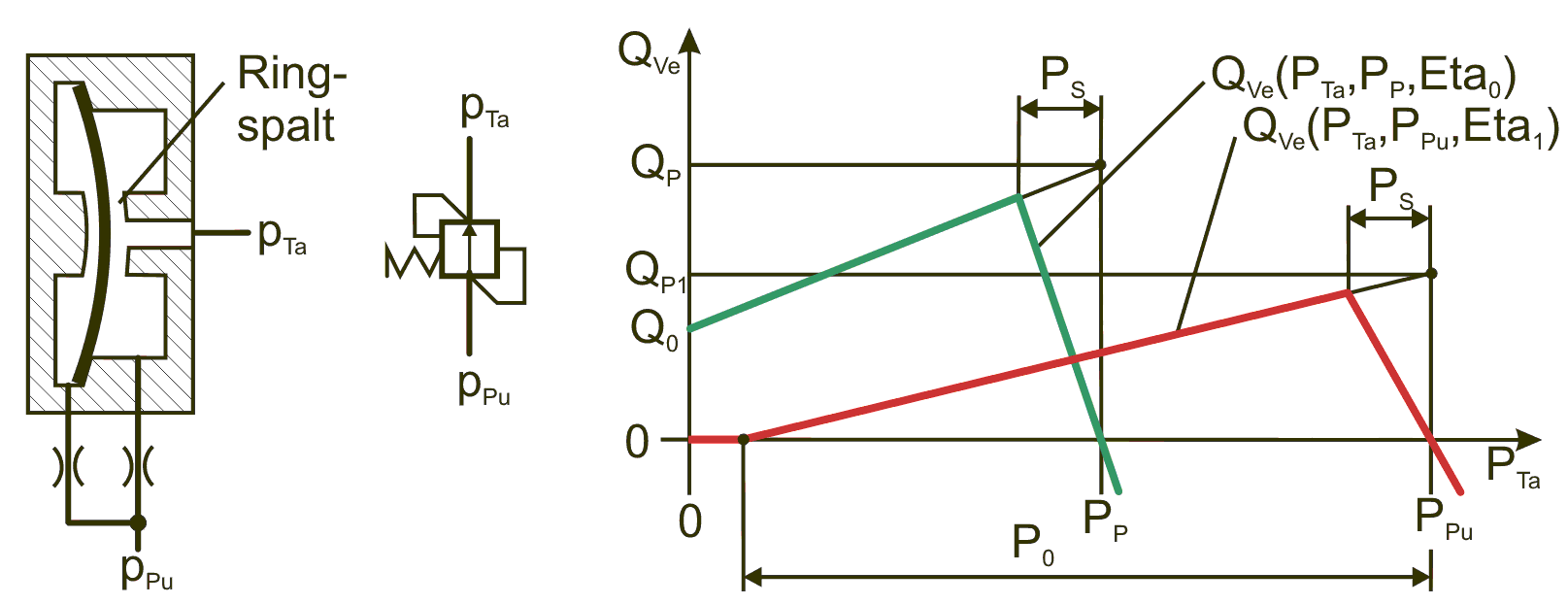
Bild 2.180: Dimensionslose Standardkennlinie (grün) und dimensionslose umgerechnete und erweiterte Kennlinie (rot) eines PM-Reglers ohne Rückschlagventile
In der Regel werden die Kennwerte für den PM-Regler in dimensionsbehafteten Parametern vorliegen und so auch in das Programm eingegeben werden. Da das Programm intern grundsätzlich mit dimensionslosen Daten arbeitet, müssen diese mindestens intern umgerechnet werden. Deshalb werden hier die erforderlichen Formeln angegeben, die SIRIUS verwendet. Aus Gründen der durchgehenden Wahlfreiheit der Art der Dateneingabe können die dimensionslosen Parameter auch direkt dimensionslos eingegeben werden und erscheinen so an der Programmoberfläche.
Die in SIRIUS benötigten Parameter für den PM-Regler werden mit den Gleichungen (2.708) bis (2.718) dimensionslos gemacht.
Dynamische Viskosität η0 bei Aufnahme der Reglerkennlinie

Pumpendruck bei Aufnahme der Kennlinie
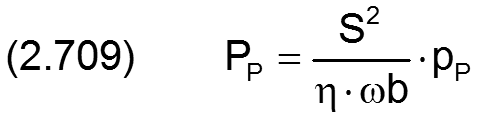
Differenzdruck zwischen Pumpendruck und dem Druck am Scheitelpunkt S der Kennlinie, der Stelle des maximalen Ölstroms,

Druckdifferenz zwischen Pumpendruck und Druck bei linker Nullstelle der Kennlinie
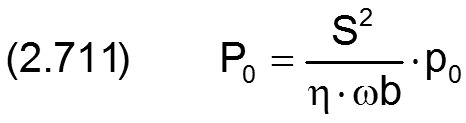
Ölstrom Q0 bei Pumpendruck PP, Taschendruck PTa=0 und Schmiermittelviskosität Eta0
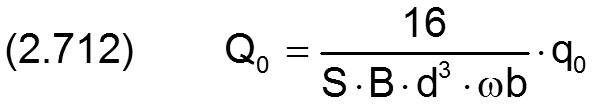
Theoretischer Ölstrom QP bei Pumpendruck PP, Taschendruck PTa=PP und Schmiermittelviskosität Eta0
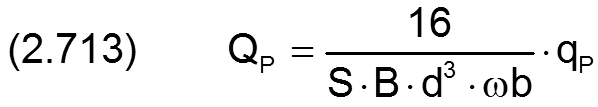
Dynamische Viskosität Eta1 am Eingang des PM-Reglers im Betrieb

Theoretischer Ölstrom QP1 bei aktuellem Pumpendruck PPu, Taschendruck PTa=PPu und aktueller Schmiermittelviskosität Eta1 am Eingang des PM-Reglers
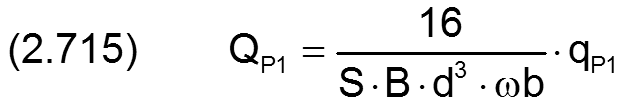
Steigung des aufsteigenden Astes der Kennlinie
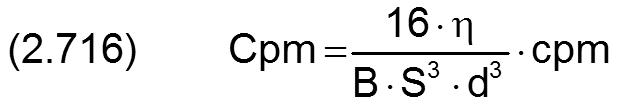
Laminarer Widerstand des maximal geöffneten PM-Reglers
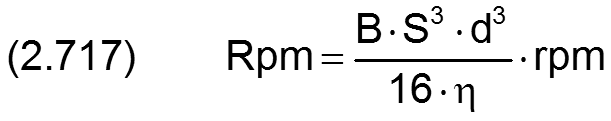
Ölstrom durch den PM-Regler
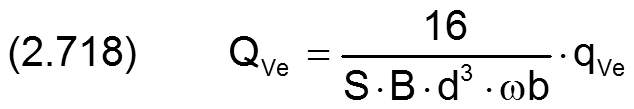
Die Gleichung (2.319) für den theoretischen Ölstrom qP1 lässt sich mit den oben angegebenen Gleichungen in die dimensionslose Form bringen

Die Gleichung (2.320) für die Steigung cpm des aufsteigenden Astes der umgerechneten Kennlinie lässt sich mit den oben angegebenen Gleichungen in die dimensionslose Form bringen
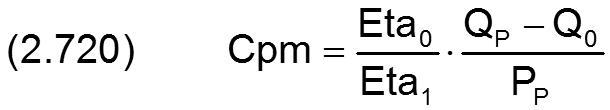
Die Gleichung (2.321) für den laminaren Widerstand rpm der umgerechneten Kennlinie des maximal geöffneten Reglers lässt sich mit den oben angegebenen Gleichungen in die dimensionslose Form bringen
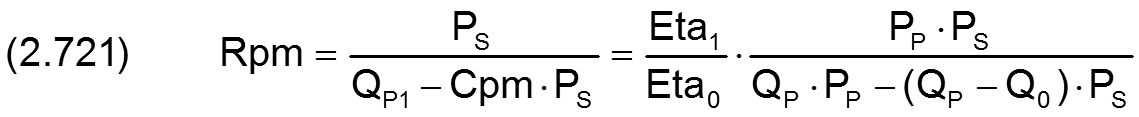
Die Gleichung (2.322) für den Abstand p0 des linken Nullpunktes der Kennlinie vom Pumpendruck pPu lässt sich mit den oben angegebenen Gleichungen in die dimensionslose Form bringen
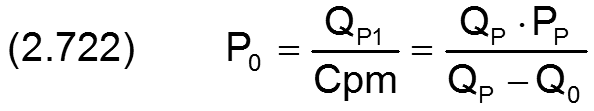
Mit diesen Parametern kann die dimensionslose idealisierte Kennlinie des PM-Reglers ohne Rückschlagventil (Bild 2.180) für beliebigen Pumpendruck PPu und beliebige Viskosität Eta1 angegeben werden durch

und entsprechend auch die Kennlinie für einen PM-Regler mit Rückschlagventil
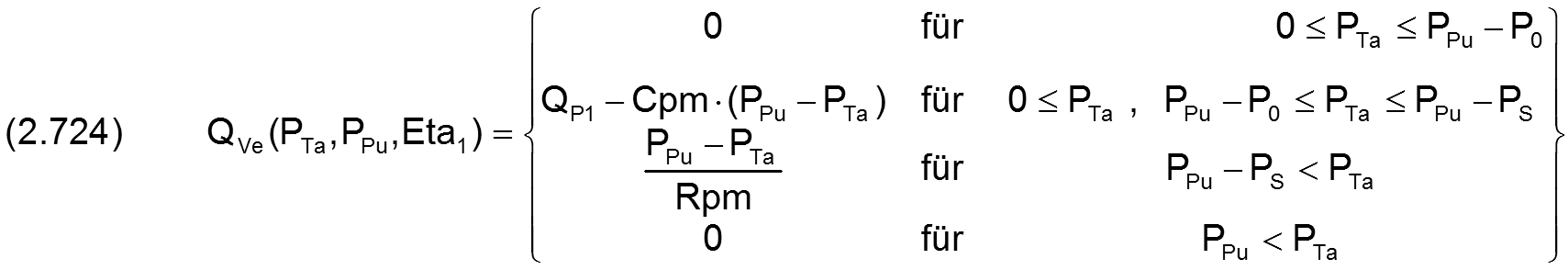
Bei einem Druckverlust pVeVer = pPu - pTa ist die Verlustleistung leiVeVer im PM-Regler gegeben durch

Mit den Formeln für die einzelnen Äste der Kennlinie z.B. für den PM-Regler ohne Rückschlagventil gemäß Gleichung (2.723) lässt sich die Gleichung für die Verlustleistung im Regler weiter konkretisieren

zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6.3 Bilanz der Ölströme des peripheren Schmiersystems
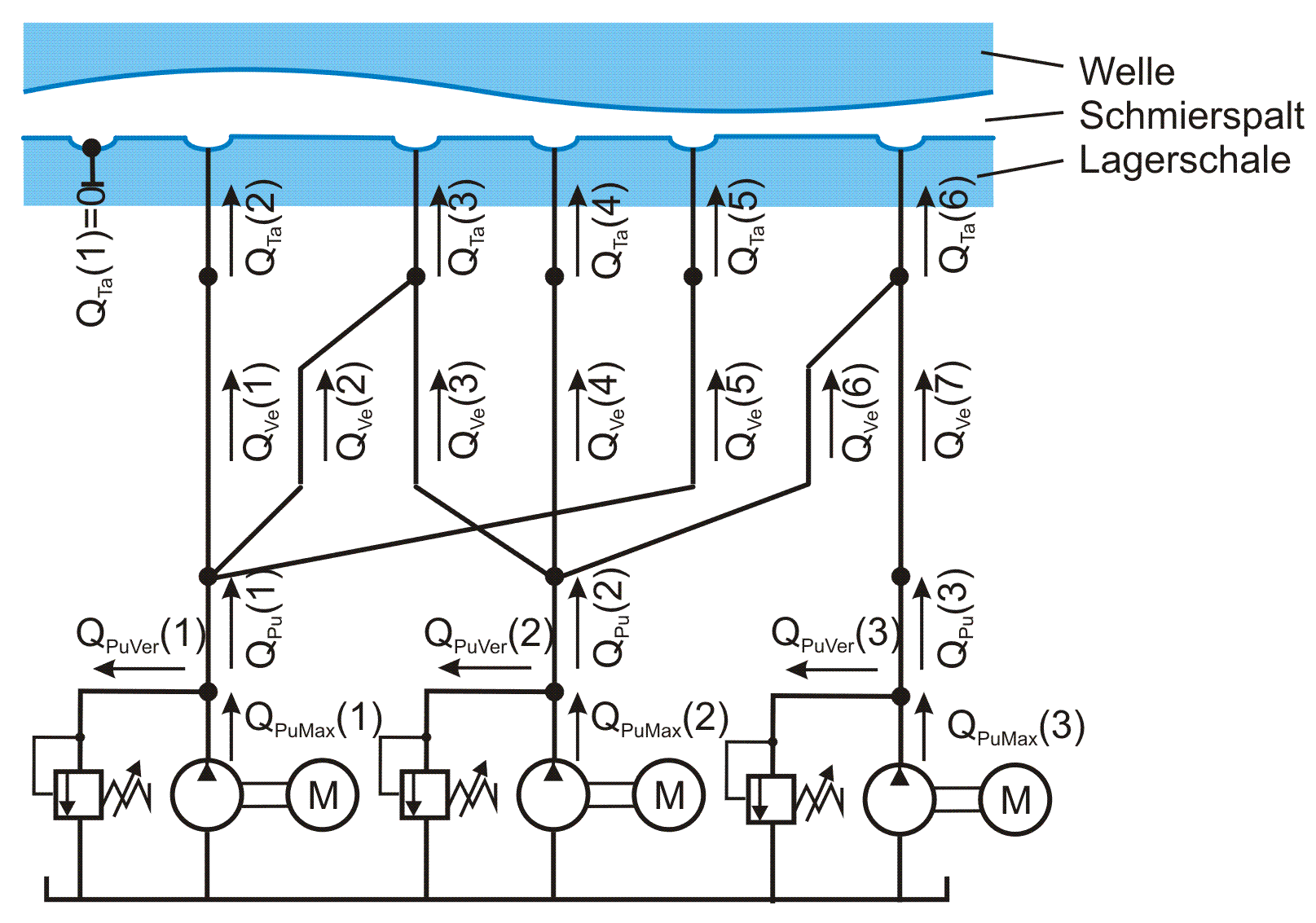
Bild 2.181: Dimensionslose Schmiermittelströme im peripheren Schmiersystem
Bild 2.181 zeigt die Netzstruktur einer möglichen Variante des Schmiersystem und die Bezeichnungen der einzelnen Teilströme. Schmiermittelströme, die von den Pumpen weg gerichtet sind, haben ein positives Vorzeichen.
Für die Pumpen Nr. JPu = 1 bis NPu, die ihren Schmiermittelstrom QPu(JPu) auf einige der NVe Leitungen mit den Ölströmen QVe(JVe) für JVe=1 bis NVe verteilen, gelten die Strombilanzen analog Gleichung (2.330).
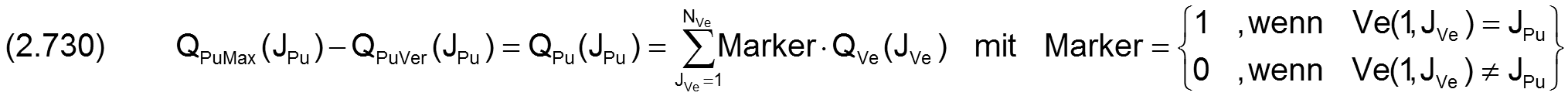
Für die Schmiertaschen Nr. JTa = 1 bis NTa, die ihren Schmiermittelstrom QTa(JTa) auf einige der NVe Leitungen mit den Ölströmen QVe(JVe) für JVe=1 bis NVe verteilen, gelten die Strombilanzen analog Gleichung (2.331).

Für den Gesamtölstrom des peripheren Schmiersystems in Richtung Schmierspalt kann nun folgende Beziehung analog Gleichung (2.332) aufgestellt werden.
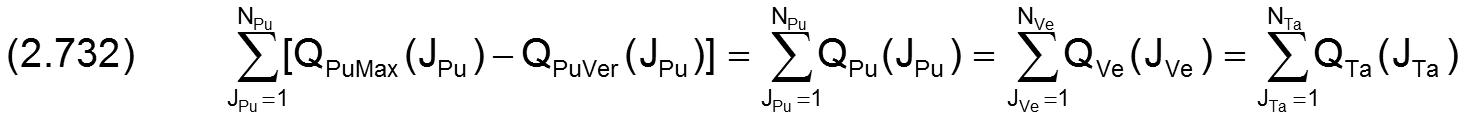
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.6.4 Energiebilanz des peripheren Schmiersystems in dimensionsloser Form
Die dimensionslose installierte Gesamtausgangsleistung aller Pumpen des peripheren Schmiersystem ist analog Gleichung (2.333) gegeben durch
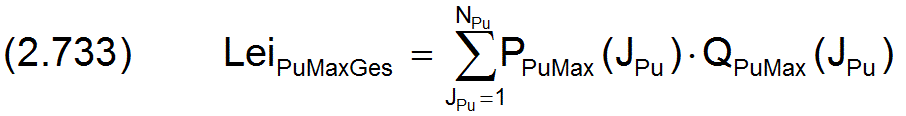
Die von den Pumpen tatsächlich bereitgestellte dimensionslose Ausgangsleistung ist analog Gleichung (2.334) gegeben durch
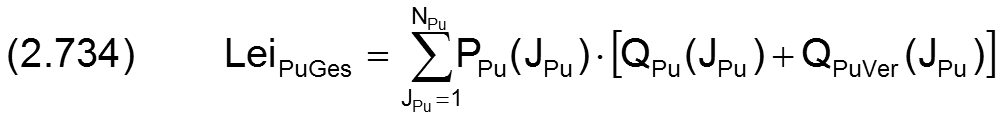
Die dimensionslose Verlustleistung der Ölströme über die Druckbegrenzungsventile an den Schmiermittelpumpen ist analog Gleichung (2.335) gegeben durch

Die Summe der dimensionslosen Leistungen, die in die Verbindungsleitungen zur Versorgung der Schmiertaschen eingespeist wird, ist analog Gleichung (2.336) gegeben durch
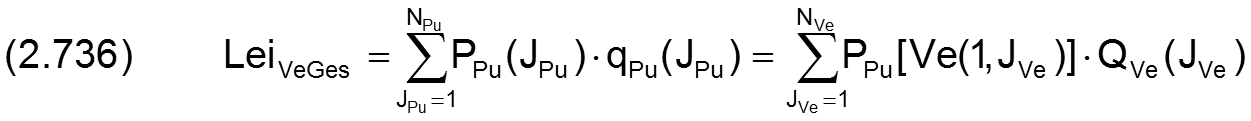
Die Summe der dimensionslosen Verlustleistungen in den Verbindungsleitungen ist analog Gleichung (2.337) gegeben durch
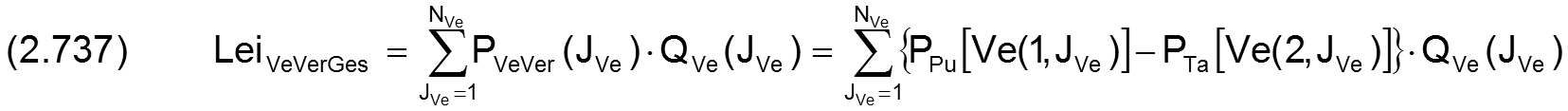
Die dimensionslose Restleistung, die dann über die Schmiertaschen dem Schmierspalt zugeführt wird, ist analog Gleichung (2.338) gegeben durch
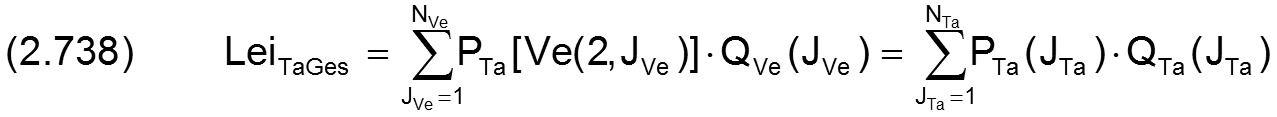
Damit lässt sich die dimensionslose Energiebilanz für das gesamte periphere Schmiermittel-Versorgungssystem aufstellen analog Gleichung (2.339)

zurück weiter
.
.
.