
Hier sind
Theoretische Grundlage zur Berechnung der Tragfähigkeit eines flüssigkeitsgeschmierten Lagers ist die hydrodynamische Schmiertheorie, die von Petroff [13], Reynolds [14] und Sommerfeld [16] begründet wurden. Sie beschreibt, wie sich in Abhängigkeit von der Geometrie des Schmierspalts, der Relativbewegung zwischen Lagerschale und Welle, der dynamischen Viskosität des Schmiermittels in der Schmierflüssigkeit und den Umgebungsdrücken an den Rändern der Schmierspaltfläche ein hydrodynamischer Druck aufbaut, der der Lagerbelastung entgegenwirkt und so den Festkörperkontakt zwischen Welle und Lagerschale und damit mechanischen Verschleiß vermeidet.
Diesen Zusammenhang beschreibt die Reynoldssche Differentialgleichung

Hier sind
| p | Druck im Schmiermittel an der Stelle (x,z) |
| h | Spalthöhe an der Stelle (x,z) |
| t | Zeit |
| vWe | Relativgeschwindigkeit zwischen Lagerschale und Welle |
| η | dynamische Viskosität der Schmierflüssigkeit |
Bei der Herleitung dieser linearen partiellen Differentialgleichung wurden folgende Annahmen getroffen:
Wendet man die Reynoldssche Differentialgleichung auf die gesamte Schmierspaltfläche an, so ergibt sich für ein stationär belastetes Lager (konstante Drehzahl, konstante Lagerbelastung und damit konstante Wellenverlagerung) ein prinzipieller Druckverlauf in der Mitte des Lagers über den Lagerumfang gemäß Bild 2.051.
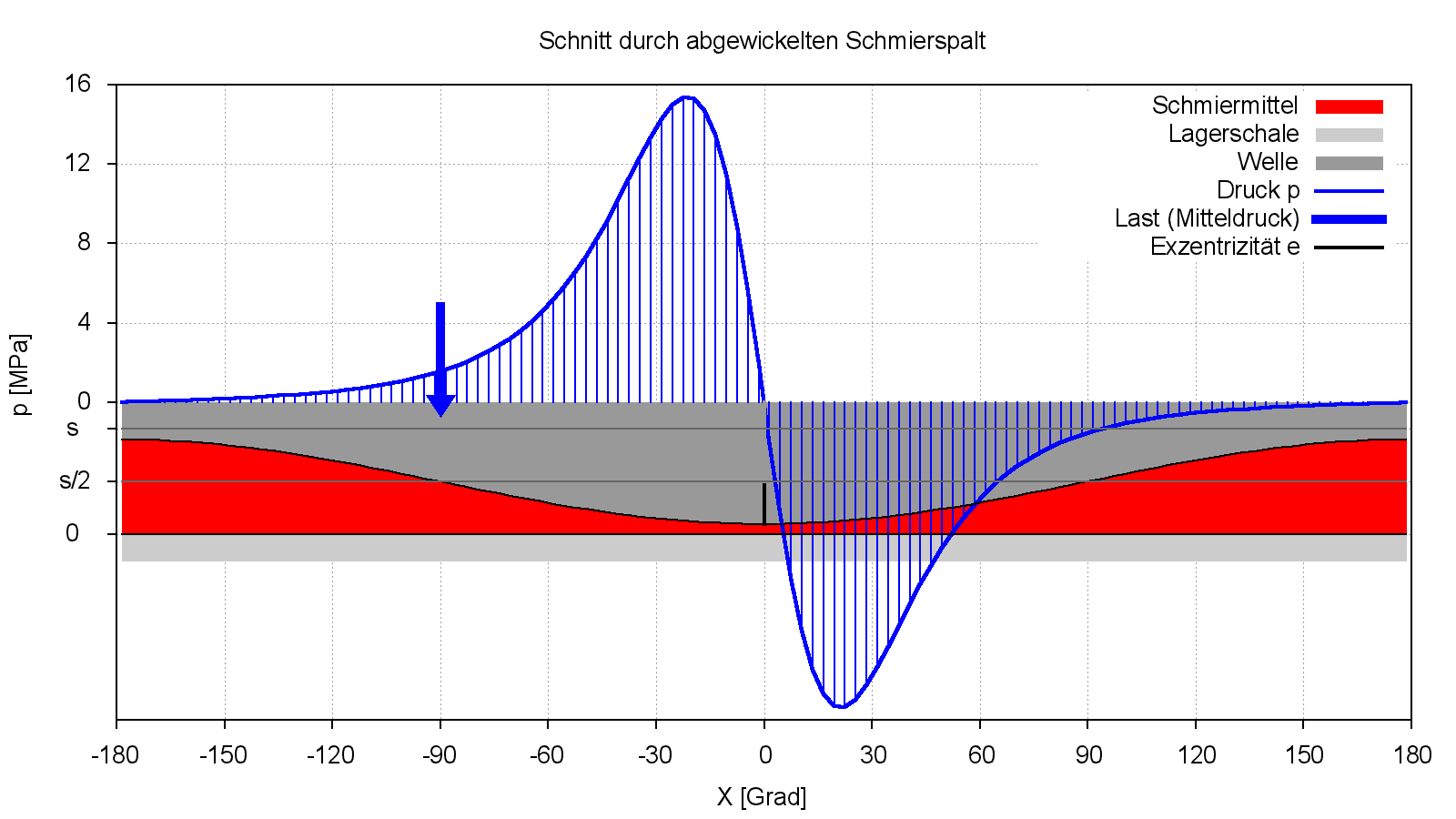
Bild 2.051: Druckverlauf p(x) und Spalthöhe h(x) in der Mitte eines stationär belasteten Lagers berechnet mit der klassischen Reynoldsschen Differentialgleichung ohne Berücksichtigung von Randbedingungen für Druckberganfang und -ende
Während im sich verengenden Schmierspaltabschnitt erwartungsgemäß ein positiver Schmierfilmdruck aufbaut, berechnet die Gleichung im Abschnitt des sich wieder erweiternden Schmierspalts negative Drücke gleichen Betrags. Diese negativen Drücke resultieren aus der Annahme eines vollständig gefüllten Schmierspalts und der Kontinuitätsbedingung, die in die Reynoldssche Gleichung eingebaut ist. Da Flüssigkeiten unter den üblichen Betriebsbedingungen eines Gleitlagers aber nicht in der Lage sind, Zugspannungen aufzunehmen, kann die klassische Reynoldssche Gleichung nur auf das Gebiet positiver Drücke angewendet werden. Deshalb müssen neben den bereits geltenden Randbedingungen weitere Randbedingungen für Druckberganfang und -ende angenommen werden.
Das Programm SIRIUS kann wahlweise mit der klassischen Reynoldsschen Gleichung arbeiten. In diesem Fall wird hier mit der "Gümbelschen Randbedingung" gearbeitet. Diese Randbedingung ist eigentlich keine echte Randbedingung. Sie funktioniert in der Weise, dass zunächst der Druckverlauf, wie oben gezeigt, für die gesamte Spaltfläche berechnet wird und anschließend alle negativen Drücke Null gesetzt werden. Diese Bedingung verstößt offensichtlich gegen die Kontinuitätsbedingung im Unterdruckgebiet und auch am Druckbergrand. Die Berechnung lässt sich aber leicht für beliebige Spaltgeometrien programmieren. Sofern keine oder nur Unterdruckgebiete geringer Ausdehnung auftreten, kann dieses Modell ausreichend sein. Solche Fälle treten z.B. bei hydrostatischen Lagern auf. Bild 2.052 zeigt eine Druckverteilung im stationären Lager unter Annahme der "Gümbelschen Randbedingung". Die Lagerbelastung f und besonders deren Richtung (hier ca. -37 grd) unterscheiden sich von dem entsprechenden Beispiel in Bild 2.051, weil die Berechnung der Lagerbelastung durch Integration des Schmierfilmdrucks über die Spaltfläche erst nach dem Null-Setzen der negativen Drücke erfolgt.
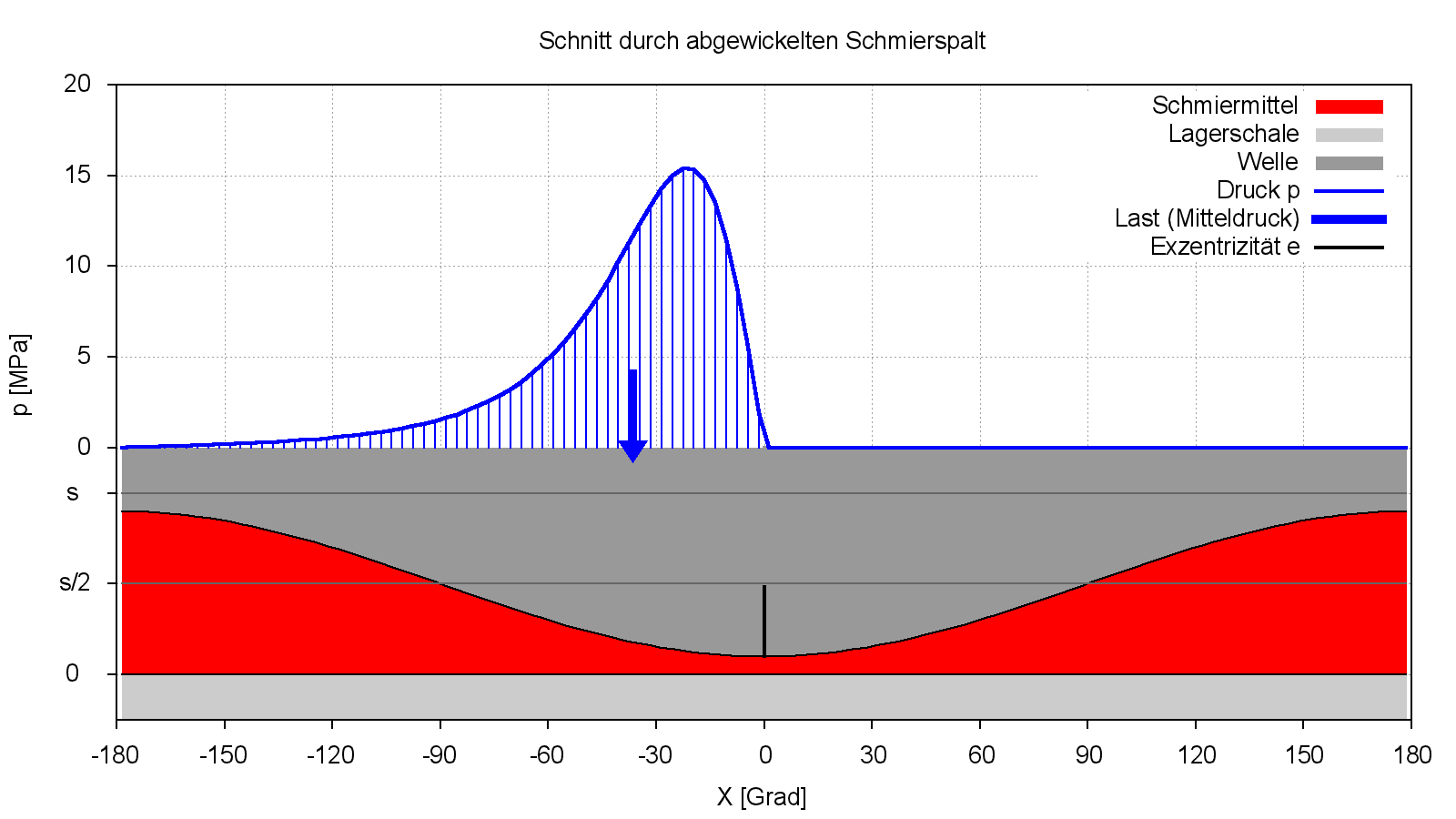
Bild 2.052: Druckverlauf p(X) und Spalthöhe h(X) in der Mitte eines stationär belasteten Lagers berechnet mit der klassischen Reynoldsschen Differentialgleichung und Annahme der "Gümbelschen Randbedingung"
Im Programm SIRIUS wurde die "Gümbelsche Randbedingung" dahingehend abgewandelt, dass der Druck im Unterdruckgebiet nicht automatisch gleich Null gesetzt wird, sondern auf die Hälfte des kleinsten Umgebungsdruckes am Lagerrand. Wenn jetzt der Umgebungsdruck > 0 angegeben wird (z.B. der absolute Umgebungsdruck von ca. 0,1 MPa) dann berechnet das Programm im gesamten Schmierspalt Drücke, die immer etwas größer als Null sind. Das hat den praktischen Vorteil, dass es möglich ist, zunächst mit der einfacheren und schnelleren Berechnung der klassischen linearen Reynoldsschen Gleichung zu arbeiten und anschließend mit dem genaueren Modell der erweiterten Reynoldsschen Gleichung die Lösung weiter zu verbessern. Drücke=0 im Schmierspalt verträgt die erweiterte Reynoldssche Gleichung nicht und können deshalb auch nicht als Anfangswerte für eine weitere Iteration verwendet werden.
Setzt man bei Annahme der klassischen Reynoldsschen Gleichung in üblicher Weise den Druck am Lagerrand gleich Null, was SIRIUS zulässt, dann berechnet das Programm den Druckverlauf wieder in der bisher üblichen Weise, bei dem der Druck im Unterdruckgebiet den Wert Null annimmt, denn 0/2=0.
zurück weiter zur dimensionslosen DarstellungUm das Problem der Randbedingungen zu lösen und die Schmiermittelströmung im gesamten Schmierspalt abzubilden, wurde die Reynoldssche Differentialgleichung weiterentwickelt. Neben dem Modell idealer Kavitation [7],[12] wurde das Modell der Schmiermittelströmung im Lagerspalt als ein Gemisch aus einer flüssigen und einer gasförmigen Phase entwickelt [20]. Dieses Modell eines Flüssigkeits-Gas-Gemischs wird neben dem klassischen Modell im Programm SIRIUS angewendet.
Hier werden die Annahmen aus dem vorhergehenden Abschnitt (2.1.3.1) um folgende ergänzt:
Daraus lässt sich die erweiterte Reynoldssche Differentialgleichung herleiten in der Form
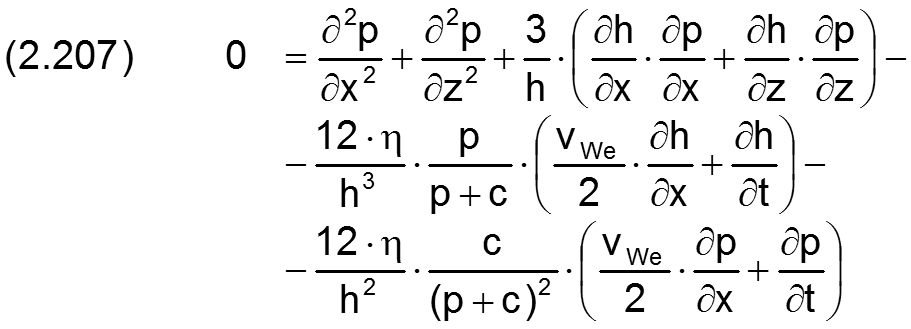
Die ausführliche Herleitung der Gleichung und Begründung des Modells ist zu finden in [20].
Zur Beschreibung des Zustandes des Flüssigkeits-Gas-Gemischs ergeben sich zwei neue Parameter, der Füllungsgrad F und die Mischungskonstante c.
Ein Volumenelement volGe im Schmierspalt enthält den Volumenanteil volFl an flüssiger Phase und den Volumenanteil volGas an gasförmiger Phase und es gilt
![]()
Dann ist der örtliche Füllungsgrad F definiert durch
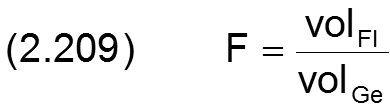
Während volFl wegen der angenommenen Inkompressibilität konstant ist, verändert sich volGas mit veränderlichem Druck und deshalb auch volGe. Damit wird der örtliche Füllungsgrad F(x,z) eine variable Größe über die Schmierspaltfläche.
Für die Gasphase soll die isothermische Zustandsänderung gelten, d.h.
![]()
Es wird der Parameter c definiert durch
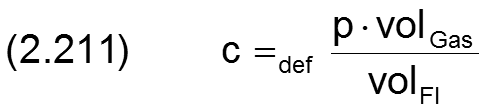
Da Zähler und Nenner des Verhältnisses gemäß der gemachten Annahmen konstant sind, ist auch der Parameter c eine konstante. Er wird als Mischungskonstante c bezeichnet und quantifiziert das konstante Mengenverhältnis von flüssiger und gasförmiger Phase im Flüssigkeits-Gas-Gemisch.
HINWEIS: Die Mischungskonstant c quantifiziert in diesem Modell einen physikalischen Sachverhalt und es entsteht beim Anwender die Frage: Welchen Wert nimmt diese Konstante unter konkreten Lagerbedingungen an und gibt es Messwerte für diesen Parameter? Dem Autor sind keine konkreten Messergebnisse zu diesem Parameter bekannt. Die Arbeit mit dem Modell eines Flüssigkeits-Gas-Gemischs hat aber gezeigt, dass der Wert für c in einem großen Intervall kaum Einfluss auf die Berechnungsergebnisse der Druckverteilung im Schmierspalt hat und es deshalb von untergeordneter Bedeutung ist, mit welchem konkreten Wert gearbeitet wird. Deshalb ist es glücklicher Weise auch nicht erforderlich durch Messungen diesen Wert zu ermitteln. Sinn der Einführung dieses Modell ist die Simulation der Kavitation im sich erweiternden Schmierspalt und das kann mit sehr verschiedenen Werten für die Mischungskonstante c erreicht werden.
Die Größe des Wertes c kann aber von Bedeutung sein für die Stabilität des in SIRUS angewendeten Berechnungsverfahrens. Einerseits erreicht man mit kleinen Werten für c, dass der Flüssigkeitsrückstau am Druckberganfang gut abgebildet wird, wie im Bild 2.054 gut zu erkennen ist. Andererseits neigt das Berechnungsverfahren genau an dieser Stelle auch zu numerischen Instabilitäten. Durch größere Werte für c wird der Verlauf des Schmierfilmdrucks p im Schmierspalt abgerundet. Dadurch arbeitet das nummerische Verfahren stabiler. Zusammenfassend kann also gesagt werden, dass der konkrete Wert von c für das eigentliche Berechnungsergebnis von untergeordneter Bedeutung ist, aber dem Anwender mit der Variation dieses Wertes eine Möglichkeit in die Hand gegeben wird, auftretende Instabilitäten des Näherungsverfahrens zu unterdrücken.
Die Berechnungen mit verschiedenen Mischungskonstanten zeigen nebenbei auch noch, dass es aus mechanischer Sicht kein Problem ist, ein Lager mit verschäumtem Öl zu schmieren, weil dadurch die Tragfähigkeit kaum sinkt. Das bedeutet aber nicht, dass Gasblasen im Schmiermittel generell unbedenklich sind. So können z.B. Luftblasen im Schmiermittel, die u.a. Sauerstoff enthalten, unter den hohen Drücken im Schmierfilm mit den Kohlenwasserstoffverbindungen des Mineralöls zu chemische Reaktionen führen, die das Schmiermittel schädigen.
Die Gleichungen (2.208) und (2.211) ergeben das Druck-Volumen-Gesetz des Flüssigkeits-Gas-Gemischs,
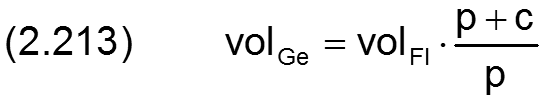
welches in Bild 2.053 qualitativ dargestellt ist. Von der Größe der Mischungskonstanten c hängt ab, wie stark sich die Kurve an ihre beiden Asymptoten anschmiegt.
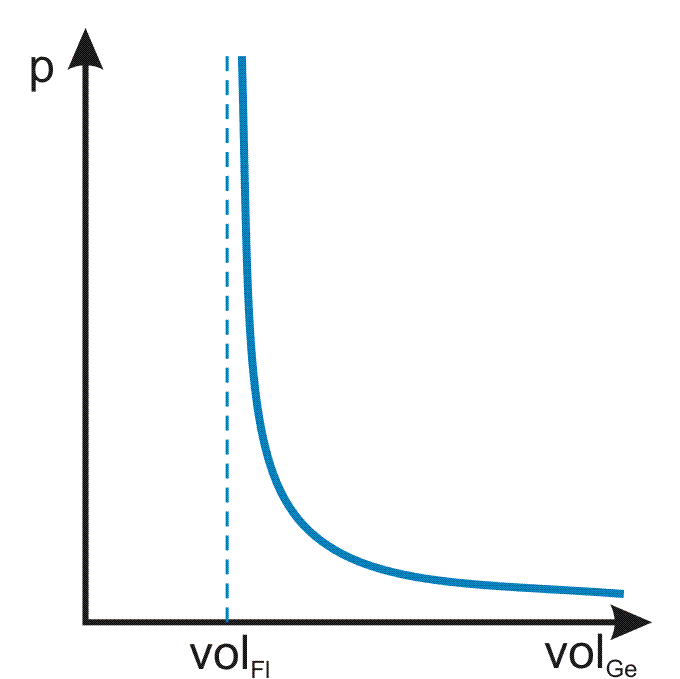
Bild 2.053: Druck-Volumen-Diagramm des Flüssigkeits-Gas-Gemischs
Die Gleichungen (2.209) und (2.213) ergeben den Zusammenhang zwischen dem Schmierfilmdruck p und dem örtlichen Füllungsgrad F
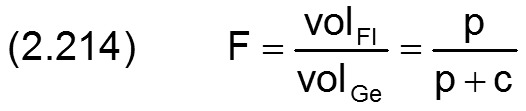
Für die flüssige Phase wird die konstante Viskosität η angenommen. Das Flüssigkeits-Gas-Gemisch wird ebenfalls als Newtonsche Flüssigkeit mit der Viskosität ηGe angenommen. Die Viskosität ηGe ergibt sich, indem die Viskosität des Gemischs proportional zum vorhandenen Blasenvolumen reduziert wird (entsprechend der Annahme s.o.). Daraus folgt
![]()
Da der Füllungsgrad F eine Funktion des Druckes ist (2.214), ist die Viskosität ηGe des Gemischs ebenfalls eine Funktion des Druckes
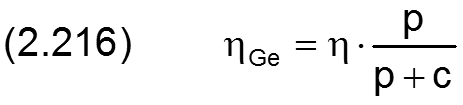
Bild 2.054 zeigt eine Druckverteilung p(X) in Lagermitte über den Umfang berechnet durch das Programm SIRIUS mit dem Modell eines Flüssigkeits-Gas-Gemischs im Schmierspalt. Außerdem wird die zugehörige Spaltgeometrie h(X) und darin die entsprechenden Anteile flüssiger Phase (rot) und gasförmiger Phase (gelb) dargestellt.
Dass hier die flüssige Phase an der Lagerschale haftend und die gasförmige Phase an der Welle haftend dargestellt ist, ist einer besseren Anschaulichkeit dieser quasi bildlichen Darstellung geschuldet und entspricht nicht der physikalischen Wirklichkeit. Beobachtungen an Lagern mit durchsichtigen Lagerschalen haben gezeigt, dass im Unterdruckgebiet der Schmierfilm aufreißt in stochastisch verteilte Gebiete, die mit Flüssigkeit oder mit Gas gefüllt sind. Sowohl die flüssige Phase als auch die Gasblasen erstrecken sich dabei jeweils über die gesamte Spalthöhe an der entsprechenden Stelle [4].
Das Demonstrationsbeispiel in Bild 2.054 stellt den Druckverlauf in einem Lager ohne Schmiertaschen dar. Hier ist der Beginn des Druckaufbaus durch einen Flüssigkeitsstau charakterisiert, ähnlich wie er vor dem Rad eines Autos zu beobachten ist, das durch eine Pfütze fährt. Hier hat der Druckverlauf quasi einen Knick und die Flüssigkeitsverteilung h·F bzw. der Füllungsgrad F macht einen Sprung. Diese Stelle stellt für das numerische Verfahren zu Berechnung der Druckverteilung im Schmierspalt die größte Herausforderung dar und ist gelegentlich Ausgangspunkt von numerischen Instabilitäten. (Ausführlicher dazu siehe Abschnitte 4.9.2.1 und 4.9.2.2)
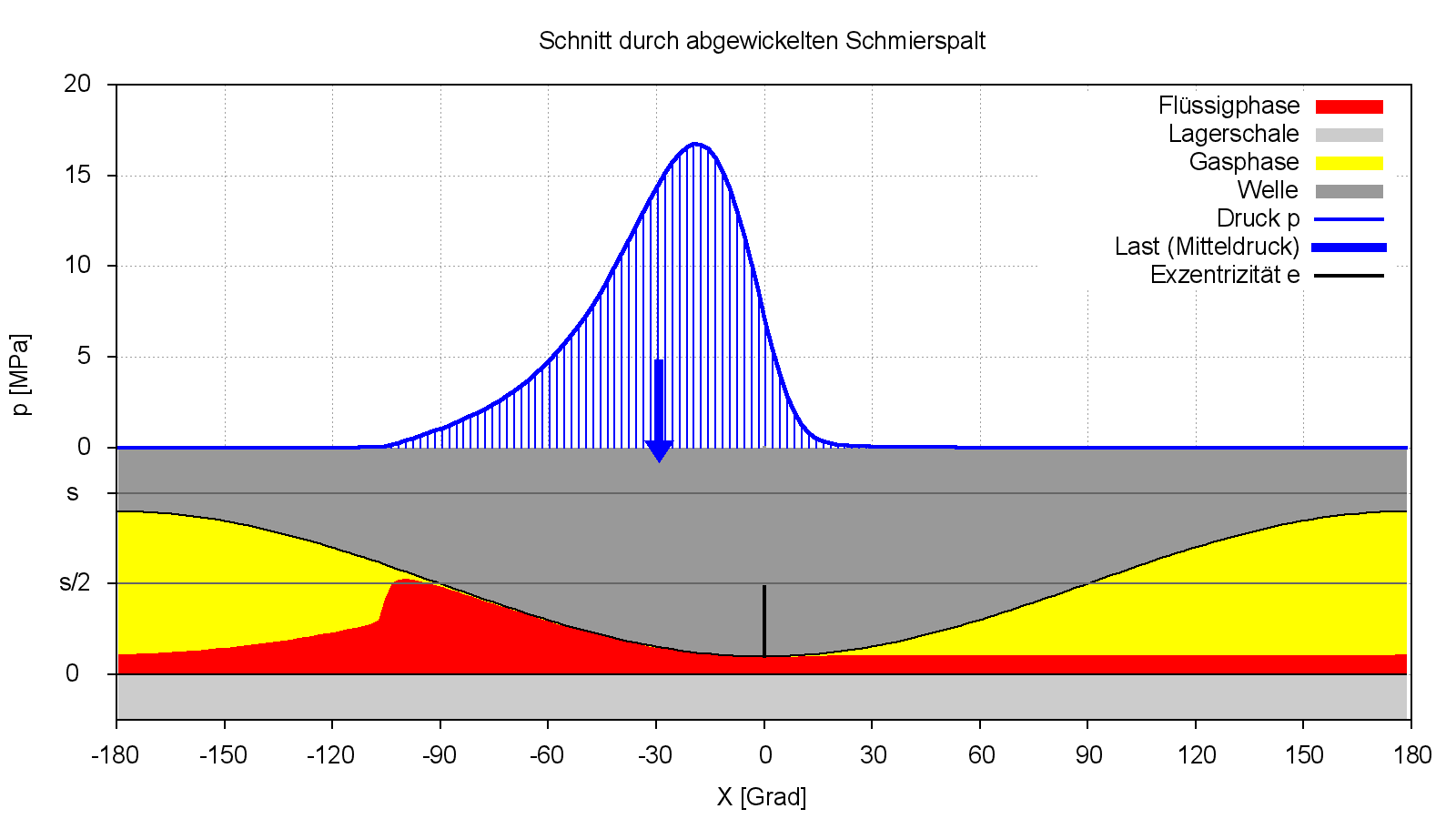
Bild 2.055 zeigt nun noch zu dem gleichen Demonstrationsbeispiel wie in Bild 2.054 eine perspektivische Darstellung des Druckverlaufs p(JX,JZ) sowie die Spalthöhe h(JX,JZ) und darunter die Flüssigkeitsverteilung hF(JX,JZ) über das abgewickelte Gitternetz der Schmierspaltfläche (NX·NZ). In dem gezeigten Beispiel ist das Lager in axialer Richtung symmetrisch. Deshalb ist hier nur der halbe abgewickelte Schmierspalt dargestellt. Die Symmetrieebene liegt bei z=0.
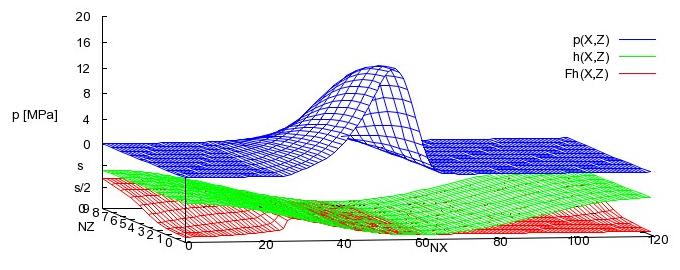
Bild 2.055: Druckverteilung p(JX,JZ), Spalthöhe h(JX,JZ) und Flüssigkeitsverteilung hF(JX,JZ) über die abgewickelte Schmierspaltfläche (NX·NZ)
Da in diesem Beispiel noch keine Schmiertaschen vorgesehen sind, wird das Lager nur von den Lagerrändern her aufgrund des geringen Druckgefälles zwischen Umgebungsdruck und Unterdruckgebiet mit Schmiermittel versorgt. Da sich insbesondere bei stationär belasteten Lagern im Unterdruckgebiet entgegen der Annahme im Modell gern Gasblasen ansammeln und damit das geringe Druckgefälle zwischen Umgebungsdruck und Unterdruckgebiet weiter reduziert wird, ist es nicht ratsam, sich auf diese unzuverlässige Schmiermittelversorgung von den Rändern her zu verlassen. Statt dessen sollten regelmäßig an geeigneten Stellen Schmiertaschen angeordnet werden, die im Programm SIRIUS an beliebiger Stelle, in beliebiger Größe und beliebiger Form berücksichtigt werden können. (Siehe dazu die Abschnitte 4.4.8 und 3.4.2.)
zurück weiter zur dimensionslosen DarstellungAls Lagerbelastung werden nachfolgend die Lagerkräfte f1, f2 und die Kippmomente mo1, mo2 angesehen , die von außen auf die Welle wirken und über die Welle mit dem Schmierfilmdruck an der Wellenoberfläche im Gleichgewicht stehen. Man kann sie auch als die Kräfte und Momente interpretieren, die resultierend aus dem Schmierfilmdruck auf die Gleitfläche der Lagerschale wirken.
Hinzu kommt das Reibmoment moWe, das aus den Schubspannungen des zähen Schmiermittels an den Gleitflächen des Lagers resultiert.
zurück weiter zur dimensionslosen Darstellung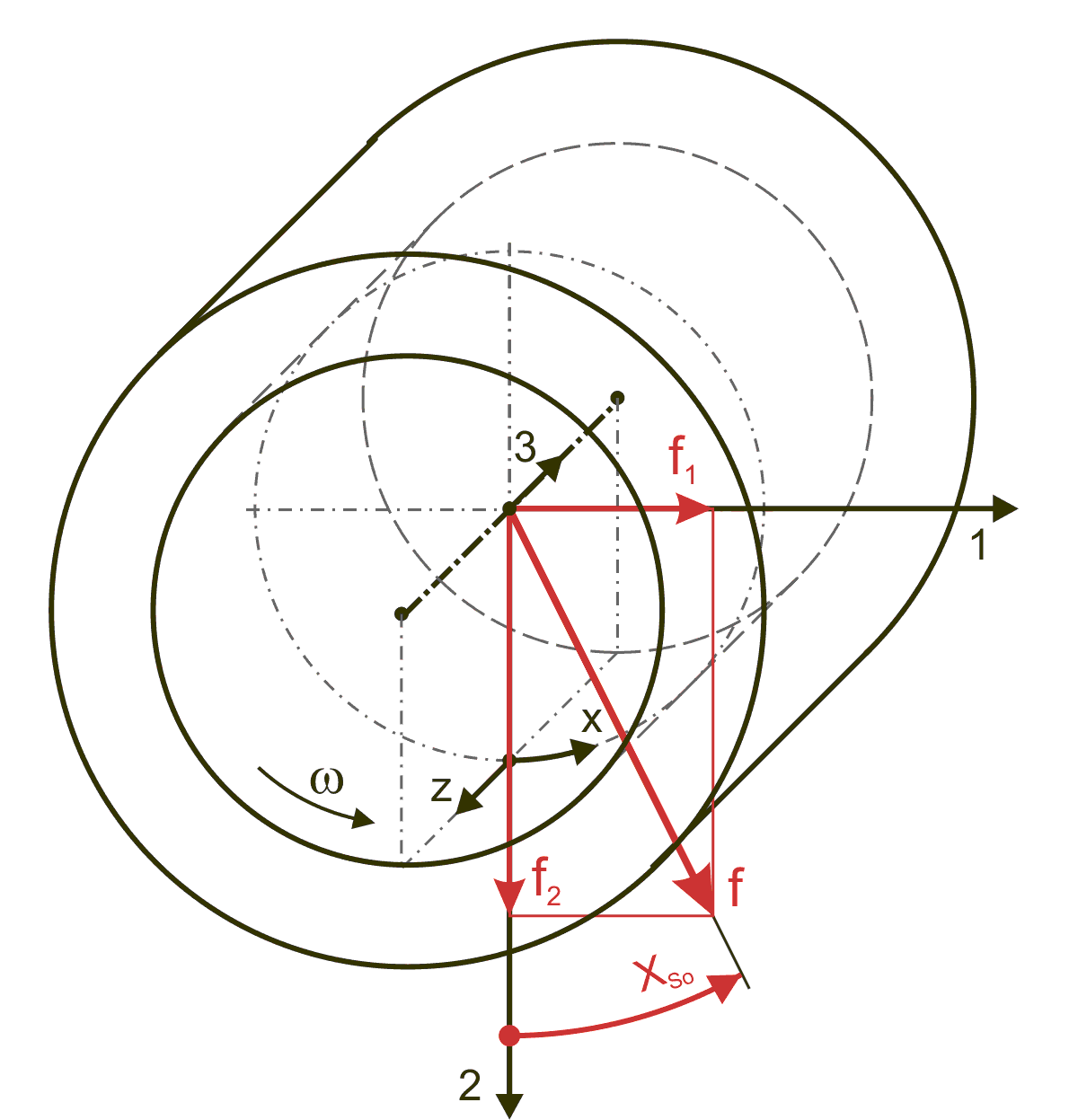
Gemäß der Definition der beiden Koordinatensysteme 1-2-3 und x-y-z ergibt sich der Zusammenhang zwischen den Lagerkräften und dem Schmierfilmdruck p(x,z) durch Integrationen über die Spaltfläche. Die Komponenten f1 und f2 sind gegeben durch die Integrale
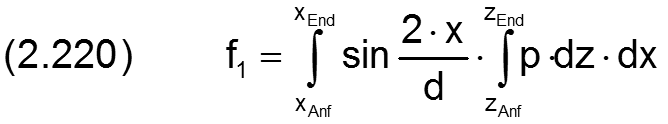
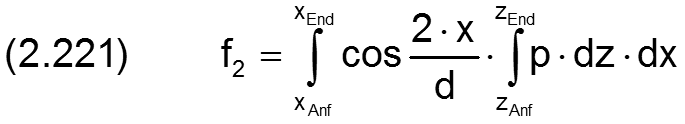
In axialer Richtung kann ein Radialgleitlager keine Kräfte aufnehmen, d.h.
![]()
Der Betrag f der resultierenden Kraft ist
![]()
Die Richtung der resultierenden Kraft ist gegeben durch den Winkel XSo, mit

Die Lagerbelastung gegeben durch die Parameter der Kraft f und der Kraftrichtung XSo bzw. durch die Komponenten der Lagerkraft f1 und f2 können als konstant oder als zeitlich variabel angenommen werden. Wenn die Verlagerungsbahn aus einem vorgegebenen (gemessenen) Verlauf der Lagerbelastung berechnet werden soll, dann können die entsprechenden Parameter der Lagerkraft für die zu berechnenden NT Zeitpunkte punktweise eingegeben werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lagers, wenn noch keine konkreten Daten für den Kraftverlauf bekannt sind, können komplette Kraftverläufe auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung des Kraftverlaufs implementiert.
![]()
![]()
mit
| f1Amp | Amplitude der Lagerkraft f1 |
| f1Mit | Mittelwert der Lagerkraft f1 |
| ω1 | Phasenwinkelgeschwindigkeit der Lagerkraft f1 |
| Φ1 | Phasenwinkel der Lagerkraft f1 zum Zeitpunkt t=0 |
| f2Amp | Amplitude der Lagerkraft f2 |
| f2Mit | Mittelwert der Lagerkraft f2 |
| ω2 | Phasenwinkelgeschwindigkeit der Lagerkraft f2 |
| Φ2 | Phasenwinkel der Lagerkraft f2 zum Zeitpunkt t=0 |
Bild 2.057 zeigt ein Beispiel für einen Kraftverlauf einer schwellenden Lagerbelastung mit den Werten f1Amp = 1 kN; f1Mit = 0 kN; ω1 = 3000 grd/s; Φ1 = -90 grd; f2Amp = 12,5 kN; f2Mit = 12,5 kN; ω2 = 3000 grd/s; Φ2 = 0 für ein Lager mit d=100 mm; b=50 mm; s=0,1mm und η=50 mPa·s.
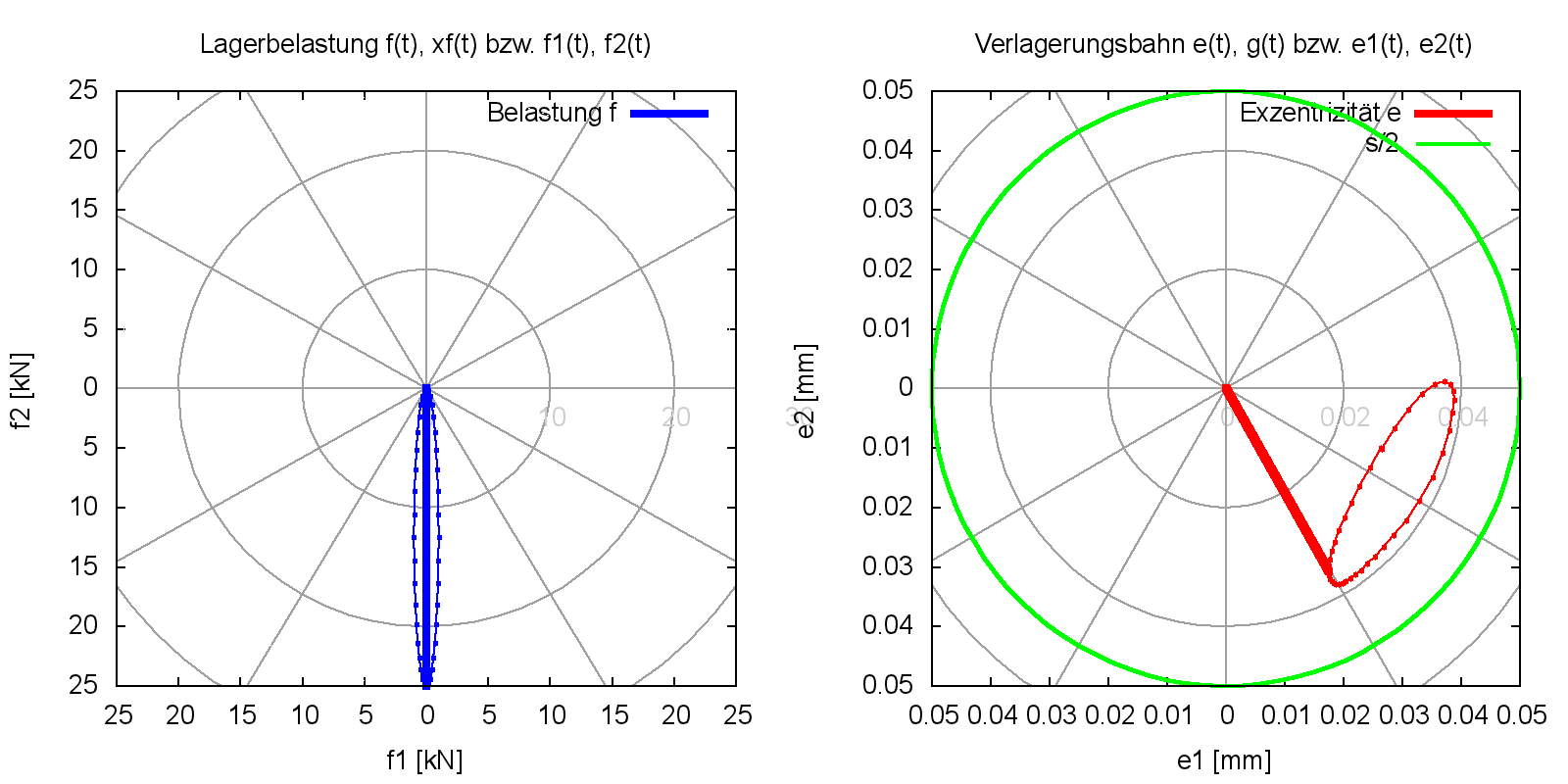
Bild 2.057: Beispiel für einen Kraftverlauf (links), der durch die Parameter einer Funktion vorgegeben wurde und rechts die zugehörige Verlagerungsbahn (Animation)
Kippmomente am Lager (Bild 2.058) entstehen bei asymmetrischer Spaltgeometrie, z.B. bei Verkantung der Welle in der Lagerschale.
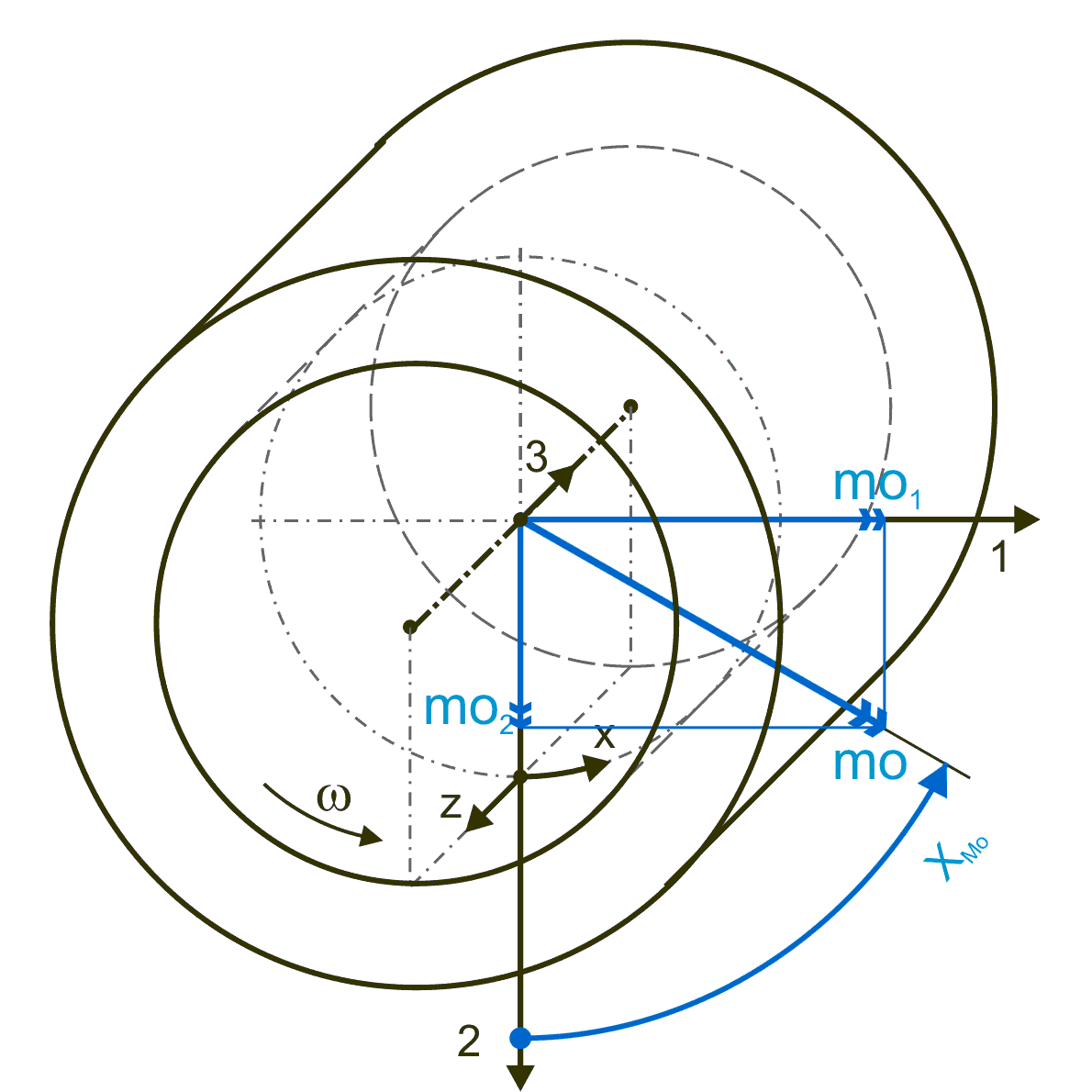
Bild 2.058: Kippmomente
Gemäß der Definition der beiden Koordinatensysteme 1-2-3 und x-y-z ergibt sich der Zusammenhang zwischen den Kippmomenten und dem Schmierfilmdruck p(x,z) durch Integrationen über die Spaltfläche.
Die Kippmomente mo1 und mo2 sind gegeben durch die Integrale
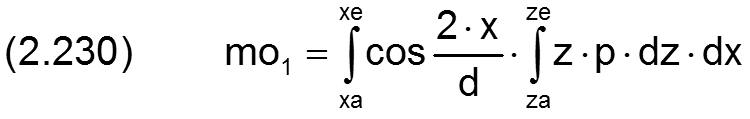
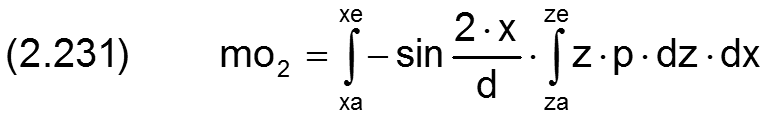
Der Betrag mo des resultierenden Kippmoments ist dann
![]()
Die Richtung des resultierenden Kippmoments ist gegeben durch den Winkel XMo, mit

Kippmomente am Lager werden im Programm SIRIUS nur als Berechnungsergebnisse geliefert, die sich aus asymmetrischer Spaltgeometrie ergeben. Sie können nicht als Eingabedaten vorgegeben werden.

Neben der mechanischen Leistung, die dem Lager durch die Schmiermittelpumpen zugeführt wird, wird dem Gleitlager auch mechanische Leistung durch das Reibmomente moWe zugeführt. Sie wird vom viel größeren Hauptenergiestrom durch die Welle an der Wellenoberfläche abgezweigt. Dieses Reibmoment ergibt sich aus dem Integral der Schubspannungen der zähen Newtonschen Schmierflüssigkeit an der Wellenoberfläche multipliziert mit dem halben Wellendurchmesser. Es gilt
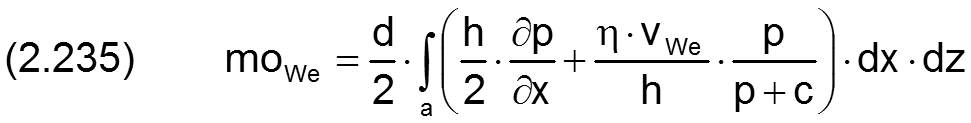
Hier ist die Fläche a=((xEnd-xAnf)·(zEnd-zAnf)-Taschenflächen), die gesamte Schmierspaltfläche unter Abzug aller Flächen der Schmiertaschen. Das ergibt sich aus der Annahme, dass die Schmiertaschentiefe viel größer ist als die Spalthöhen h(x,z) und dass deshalb die innere Reibung in den Schmiertaschen vernachlässigt werden kann.
Die Wellenreibleistung leiWe ist die mechanische Leistung, die von der Wellenoberfläche durch ihre Rotation gegen den Widerstand der Schubspannungen zwischen Wellenoberfläche und Schmierflüssigkeit auf den Schmierfilm übertragen wird, bezogen auf eine feststehende Lagerschale.

Diese mechanische Leistung wird nicht gleich an der Wellenoberfläche in Wärme umgewandelt, sondern zunächst über das Geschwindigkeitsprofil im Schmierspalt in das gesamte Schmierflüssigkeitsvolumen eingetragen. Hier wird sie dann durch die Geschwindigkeitsunterschiede der Schmiermittelschichten und der dadurch entstehenden inneren Reibung in Wärme umgewandelt.
Die nachfolgend angegebenen Gleichungen sind zum Teil bereits in der Reynoldsschen Differentialgleichung zur Berechnung des Schmierfilmdruckes verarbeitet. Sie werden auch im Rahmen der Hauptrechnung für die Formulierung der Volumenbilanz in den Schmiertaschen benötigt. Außerdem werden sie im Anschluss an die Hauptrechnung zur Berechnung weiterer wichtiger sekundärer Ergebnisse benötig. Deshalb werden dieser physikalische Sachverhalt und die daraus resultierenden Gleichungen hier ausführlich dokumentiert.
Für die Auslegung der Schmiermittelversorgung als auch die Ermittlung des Energieverbrauchs und die daraus resultierende Erwärmung des Schmiermittels bzw. des Lagers ist die Kenntnis der Ölströme durch das Lager wichtig. Deshalb sind sie bei der Auslegung eines Lagers explizit zu ermitteln.
Die Gleichungen für die Strömungsgeschwindigkeiten im Schmierspalt sind Grundlage für die Herleitung weiterer Gleichungen wie z.B. die Reynoldssche Differentialgleichung, die Bilanz der Schmiermittelströme und die Energiebilanz. Deshalb werden diese Gleichungen hier angegeben.
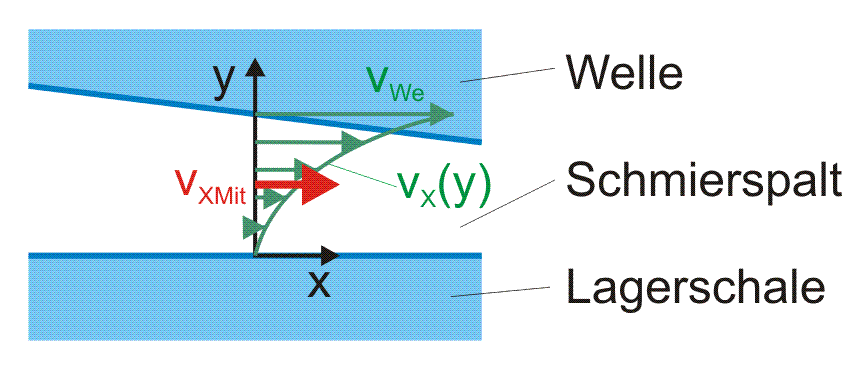
Bild 2.060: Profil der Strömungsgeschwindigkeiten über die Spalthöhe in Umfangsrichtung x
Bild 2.060 skizziert das Profil der Komponente vX(y) der Strömungsgeschwindigkeit in Umfangsrichtung x über die Spalthöhe und die daraus resultierende Komponente der mittlere Strömungsgeschwindigkeit vXMit.
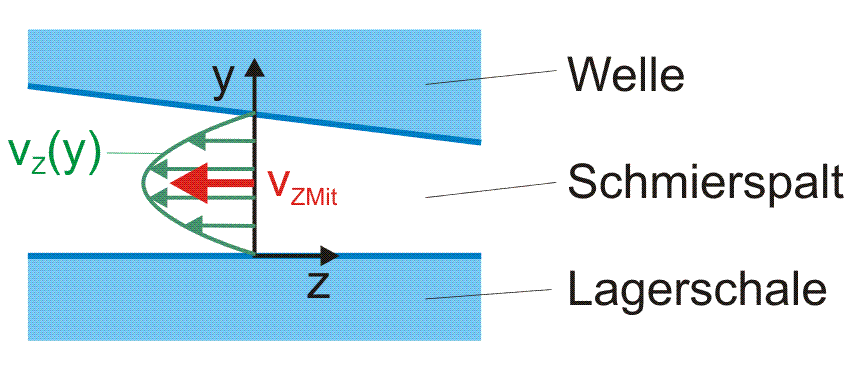
Bild 2.061: Profil der Strömungsgeschwindigkeiten über die Spalthöhe in axialer Richtung z
Bild 2.061 skizziert das Profil der Komponente vZ(y) der Strömungsgeschwindigkeit in axialer Richtung z über die Spalthöhe und die daraus resultierende Komponente der mittlere Strömungsgeschwindigkeit vZMit.
Diese Geschwindigkeitsprofile ergeben sich aus dem Kräftegleichgewicht am Volumenelement im Schmierspalt und deren Integration über y. Das Geschwindigkeitsfeld v(x,y,z) der Schmiermittelströmung im Spalt ist gegeben durch die Gleichungen für die Komponenten vX(x,y,z) und vZ(x,y,z) mit
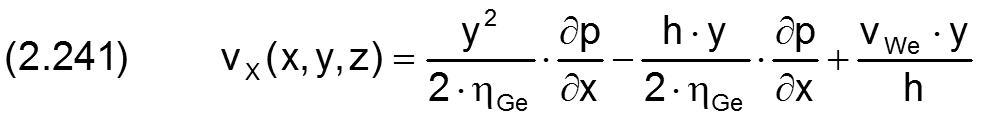
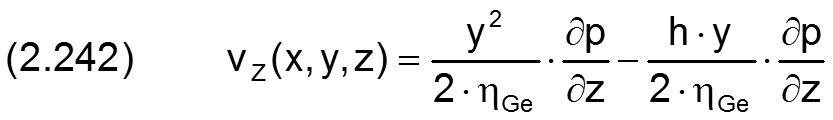
Wegen der geringen Höhe des Schmierspalts gilt für die Geschwindigkeitskomponente vY(x,y,z)
![]()
Die Integrationen dieser Geschwindigkeitsprofile über die Spalthöhe h und einsetzen der Gleichung (2.216) ergeben dann die mittleren Strömungsgeschwindigkeiten vXMit und vZMit
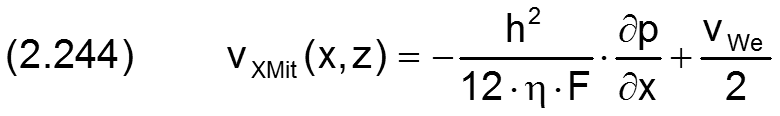
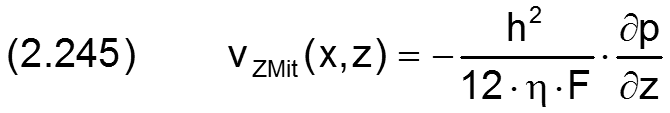
Die ausführliche Herleitung der Gleichungen ist enthalten in [20, Kap.4]
Bild 2.062 zeigt den abgewickelten Schmierspalt eines teilweise umschlossenen Lagers mit seinen 4 Rändern und seinen Ölströmen qRand1, qRand2, qRand3 und qRand4 über diese Ränder.

Bild 2.062: Abgewickelte Schmierspaltfläche mit den 4 möglichen Ölströmen über die Schmierspaltränder
Die Ölströme werden berechnet durch die Integrale
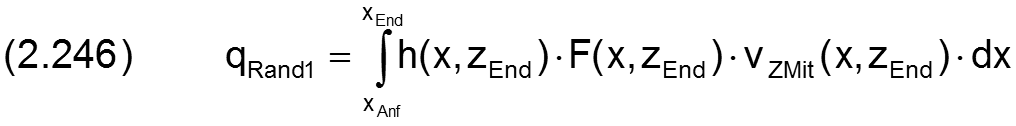
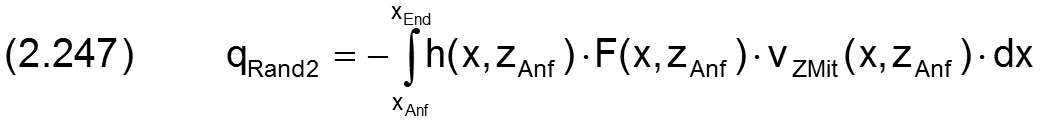
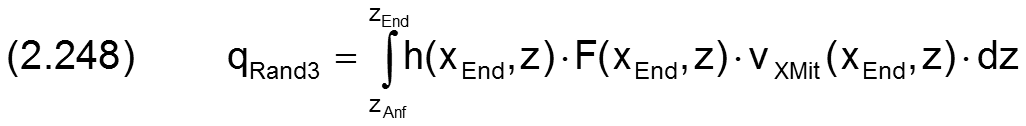
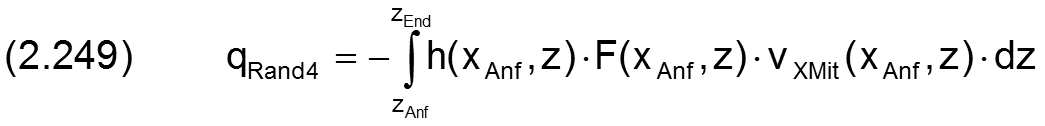
Die Ölströme aus dem Schmierspalt heraus haben hier ein positives Vorzeichen.
Indem der Füllungsgrad F berücksichtigt wird, gelten diese Gleichungen für die erweiterte Schmiertheorie mit der Annahme eines Flüssigkeits-Gas-Gemischs im Schmierspalt. Die angegebenen Ölströme qRand1 bis qRand4 enthalten dabei nur noch den Volumenanteil der flüssigen inkompressiblen Phase des Schmiermittel-Gas-Gemischs. Wird der Füllungsgrad F=1 gesetzt, gelten die Gleichungen auch für die klassische Theorie.
Da der Druck am Schmierspaltrand eines teilweise umschlossenen Lagers der konstante Umgebungsdruck pRand1 ist, sind F(xEnd,z), F(xAnf,z), F(x,zAnf) und F(x,zEnd) auch konstant und gegeben nach Gleichung 2.214 durch
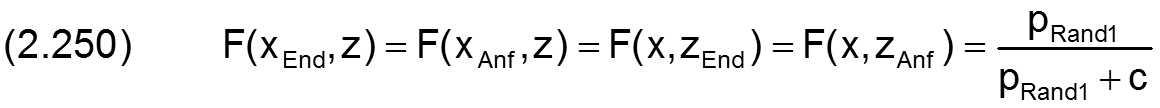
Wenn der Druckverlauf im Schmierspalt bekannt ist und so neben dem Umgebungsdruck pRand1 auch die Druckanstiege ∂p/∂x bzw. &Part;p/∂z an den Lagerrändern, lassen sich mit Hilfe der Gleichungen (2.215), (2.244), (2.245) und (2.250) die Integrale weiter konkretisieren, so dass daraus die Ölströme direkt berechnet werden können.
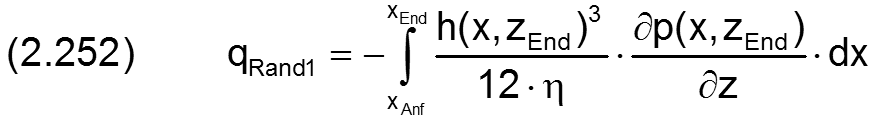
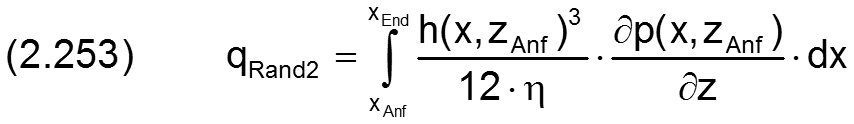
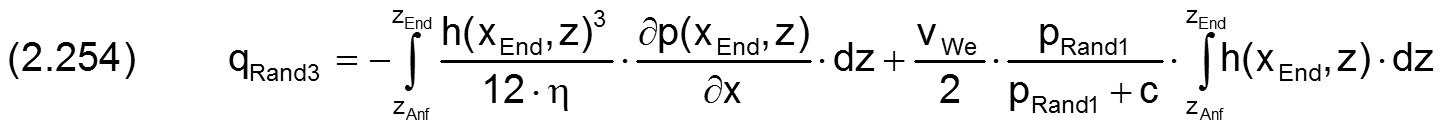
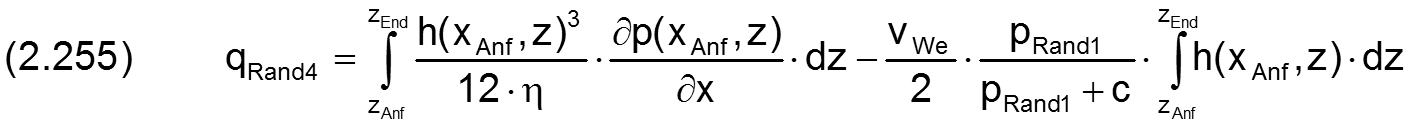
Am teilweise umschlossenen Lager ist also der Gesamtölstrom qRand über die Lagerränder gegeben durch die 4 Teilströme
![]()
Das voll umschlossene Lager hat nur die zwei Ränder bei z=zAnf und z=zEnd. Damit ergibt sich hier für das voll umschlossene Lager ein Gesamtölstrom von
![]()
Wenn das voll umschlossene Lager außerdem symmetrisch ist gilt
![]()
Die Ränder der Schmiertaschen sind, genauso wie die Lagerränder, Ränder der eigentlichen Schmierspaltfläche, über die ein Ölstrom fließt von der Schmiertasche in den Schmierspalt oder umgekehrt, je nach Druckgefälle entlang des Randes.
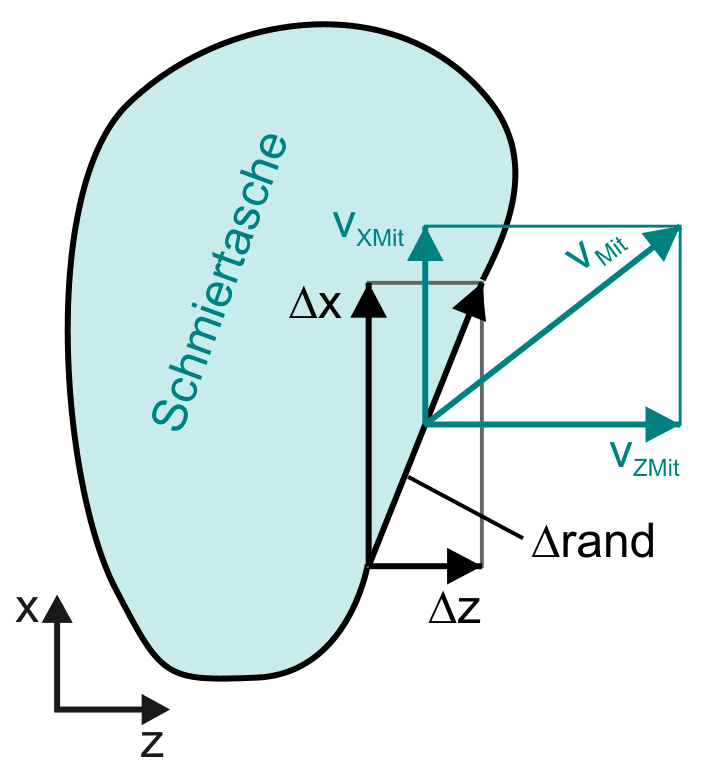
Bild 2.063: Ölstrom qTaRand über das Randelement Δrand aus einer Schmiertasche in den Schmierspalt
Bild 2.063 zeigt die Randkontur einer Schmiertasche mit einem gerichteten Randstück Δrand. Dieses Randstück ist der Vektor

Über das Randstück strömt das Öl mit einer mittleren Strömungsgeschwindigkeit vMit.
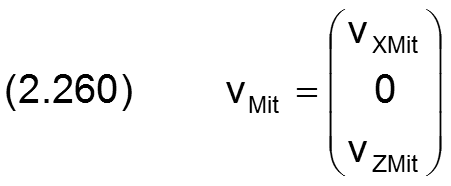
Da Schmiertaschen im Vergleich zur Schmierspalthöhe sehr tief sind, werden Strömungswiderstände innerhalb der Schmiertasche vernachlässigt. D.h., der Schmiertaschendruck pTa über die Fläche einer Schmiertasche, einschließlich dem Rand, ist konstant und damit auch der Füllungsgrad FTa der Tasche, der nach Gleichung (2.214) eine direkte Funktion vom Druck pTa ist. Er berechnet sich durch
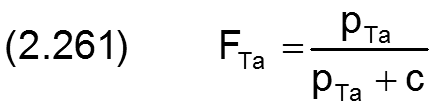
Der Teilstrom qTaRand über das Randelement ist das Vektorprodukt aus h·FTa·vMit und Δrand
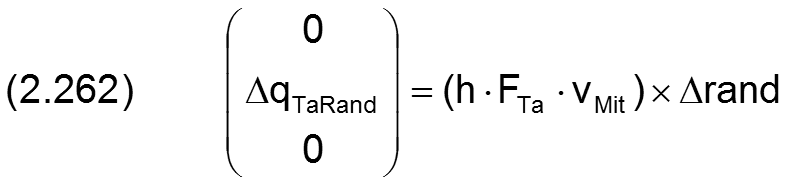
oder ausmultipliziert
![]()
Der Gesamtölstrom qTaRand aus der Tasche in den Schmierspalt ist dann das Integral über den Schmiertaschenrand
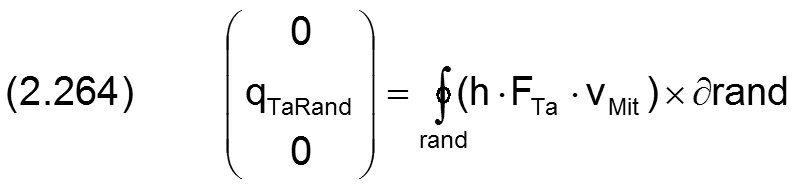
oder ausmultipliziert
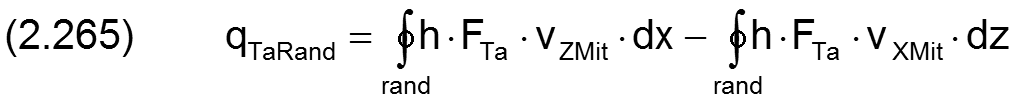
Mit den Gleichungen (2.215), (2.244) und (2.245) lässt sich auch diese Gleichung weiter konkretisieren zu
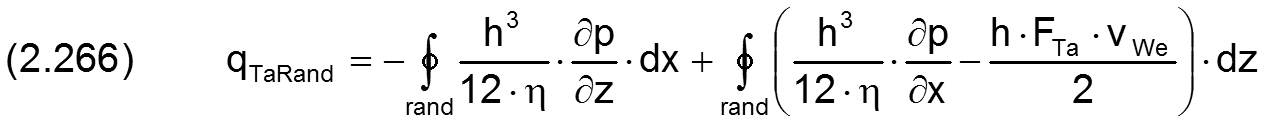
und mit Gleichung (2.261) weiter zu
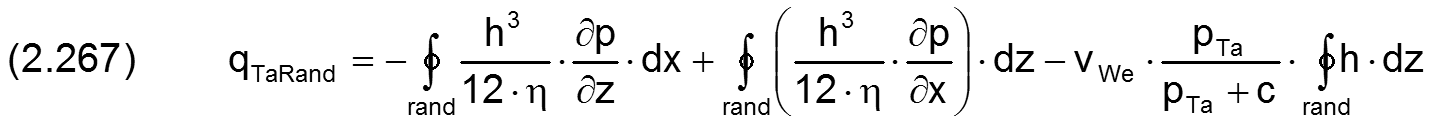
Unter Berücksichtigung eines Schmiermittel-Gas-Gemischs auch in der Schmiertasche ergibt sich das Flüssigkeitsvolumen ΔvolFlTa in einem Volumenelement der Schmiertasche durch
![]()
und seine Änderung über die Zeit durch

Die Integration über die Schmiertaschenfläche a ergibt die Änderung des gesamten Schmierflüssigkeitsvolumens
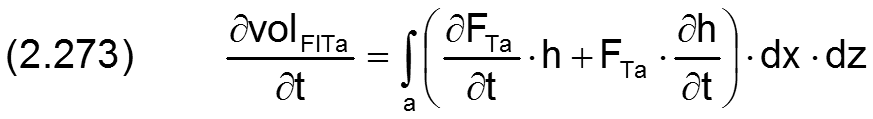
Da der Druck pTa in einer Schmiertasche als konstant über die Schmiertaschenfläche angenommen wird, ist auch der Füllungsgrad FTa in der Schmiertasche konstant. Über die Zeit müssen der Taschendruck und damit der Füllungsgrad allerdings nicht konstant sein.
So lässt sich die Gleichung umstellen

Für die klassische Schmiertheorie, bei der immer ein vollständig gefüllter Schmierspalt F=1 angenommen wird, vereinfacht sich die Gleichung zu
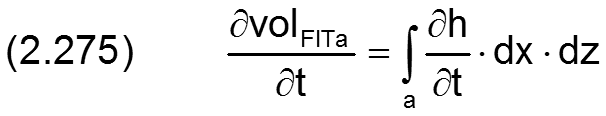
Im Programm SIRIUS können in der Lagerschale eine große Anzahl Schmiertaschen mit beliebiger Anordnung und beliebiger Randkontur berücksichtigt werden. Wenn in einem Lager NTa Schmiertaschen existieren, ist für jede dieser Taschen die Volumenbilanz der Schmierflüssigkeit aufzustellen durch die NTa Gleichungen
 |
für JTa = 1 bis NTa. |
Das Volumen volFlSpalt der flüssigen Phase des Schmiermittels im Schmierspalt wird berechnet durch
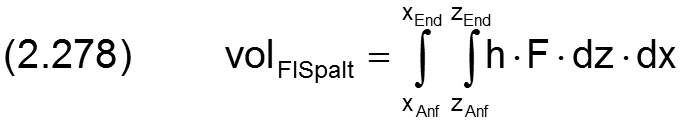
Der Gesamtfüllungsgrad des Schmierspalts ist dann gegeben durch
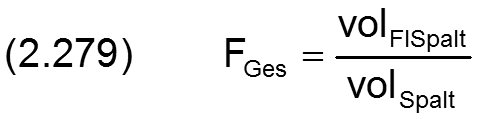
Die Summe der zu- und abfließenden Flüssigkeitsströme ist gleich der Änderung des Flüssigkeitsvolumens im Schmierspalt. Für ein teilweise umschlossenes Lager gilt
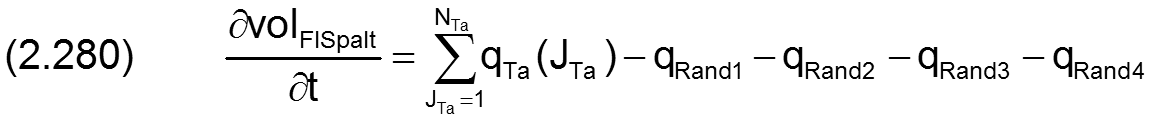
Für das voll umschlossene Lager gilt
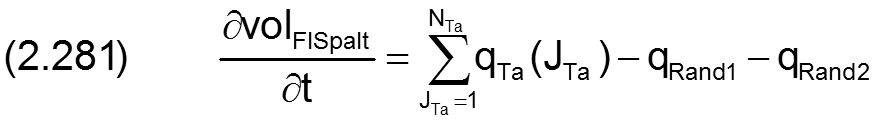
Das Differential d³leiReib der Reibleistung innerhalb eines differentiell kleinen Volumenelementes dx·dy·dz lässt sich herleiten aus dem Geschwindigkeitsprofil v(x,y,z) und den daraus resultierenden Schubspannungen. Es lässt sich berechnen durch die Gleichung

Die Integration der Gleichung (2.282) über die Spalthöhe h ergibt dann das Differential d²leiReib der Reibleistung innerhalb eines Flächenelements dx·dz des Schmierspalts. Es lässt sich berechnen durch die Gleichung
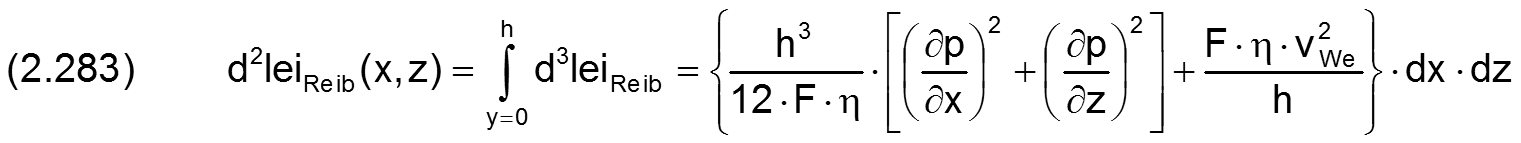
Gleichzeitig wurde hier mit Gleichung (2.215) die Viskosität ηGe des Gemischs durch η und F ersetzt.
Bildet man aus diesem Differential den partiellen Differentialquotienten nach dx und dz, so erhält man die Reibleistungsdichte über die Spaltfläche mit der man auswerten kann, in welchen Bereichen des Schmierspalts die größte Wärmeumwandlung erfolgt. Die Reibleistungsdichte ist gegeben durch

Die Integration das Differentials d²leiReib über die gesamte Schmierspaltfläche a ergibt die Reibleistung leiReib im Schmierspalt
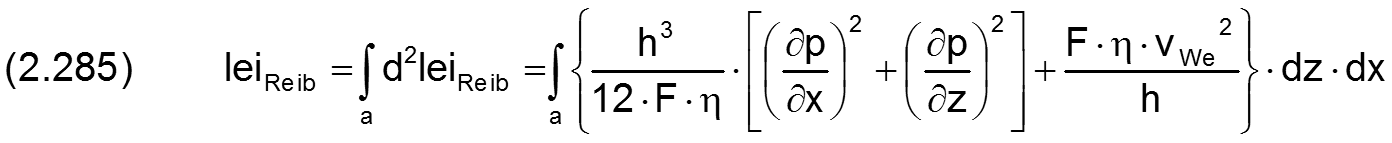
Diese Reibleistung entspricht der vollständigen Energiemenge pro Zeiteinheit, die im Schmierspalt in Wärme umgewandelt wird und im günstigsten Fall über die Erwärmung des Schmiermittels wieder aus dem Lager abtransportiert wird, aber auch das Lager erwärmen kann, bis ein Gleichgewicht der Wärmeableitung über das Lagergehäuse und die Welle entsteht.
zurück weiter zur dimensionslosen DarstellungFür den Schmierspalt kann nun die Energiebilanz aufgestellt werden. Die in das Lager über den Schmiermittelzufluss und das Wellenreibmoment einfließende mechanische Energie minus der abfließenden Energie über die Schmierspaltränder ist gleich der Reibleistung im Schmierspalt.
Für ein teilweise umschlossenes Lager gilt

Für ein voll umschlossenes asymmetrisches Lager gilt
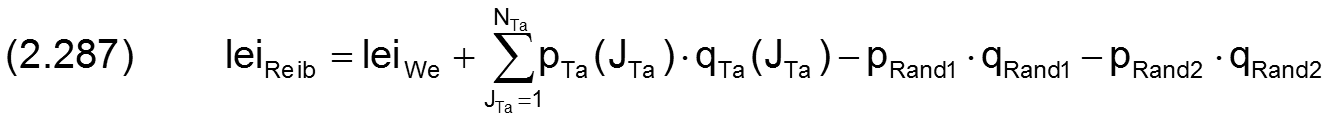
Hydrodynamisch geschmierte Lager sind Gleitlager bei denen die Schmiermittelversorgung über die Schmiertaschen (und den Lagerrand) mit niedrigem Druck im Vergleich zum maximalen Schmierfilmdruck erfolgt. Hier ist es in der Regel ausreichend, den Zufuhrdruck anzugeben, der an den Schmiertaschen herrscht, um brauchbare Berechnungsergebnisse zu erhalten. Die Schmiertaschen werden dabei vorzugsweise in dem Bereich des sich erweiternden Schmierspalts angeordnet, wo Unterdruck herrscht, und der Druckaufbau erfolgt im Bereich des sich verengenden Schmierspalts.
Hydrostatisch geschmierte Lager sind Gleitlager bei denen die Schmiermittelversorgung über die Schmiertaschen mit hohem Druck durch externe Hochdruckpumpen erfolgt. Dieser Druck muss größer sein als der größte Schmierfilmdruck, der erforderlich ist, um Welle und Lagerschale bei allen auftretenden Lasten sicher von einander zu trennen. Die Schmiertaschen sind in der Regel über die gesamte Spaltfläche verteilt. Da die Ölströme aber die Tendenz haben, vorzugsweise entlang des Weges mit dem geringsten Widerstand zu strömen, muss die externe hydrostatische Schmiermittelversorgung neben mindestens einer Hochdruckpumpe auch über hydraulische Steuer- bzw. Regelmechanismen verfügen, damit das Schmiermittel auch in die Schmiertaschen strömt, wo es gebraucht wird, nämlich in die Schmiertaschen mit dem höchsten Druck.
Da das Programm SIRIUS sowohl hydrodynamisch als auch hydrostatisch geschmierte Lager einschließlich Mischformen berechnet, ist es erforderlich, dass auch ein möglichst großes Spektrum hydrostatischer Schmiermittel-Versorgungseinrichtungen simuliert werden kann. Deshalb wurde ein peripheres Universal-Schmiersystem eingeführt, das nachfolgend beschrieben wird. Es werden die erforderlichen Formeln angegeben mit denen das physikalische Verhalten der darin enthaltenen Elemente und ihr Zusammenspiel beschrieben werden.

Bild 2.070 zeigt den hydraulischen Schaltplan einer möglichen Variante, die mit dem peripheren Schmiersystem modelliert werden kann. Die gezeigte Variante ist nicht unbedingt sinnvoll. Sie zeigt aber in einem einzigen Beispiel, was hier alles möglich ist:
Aktuell sind folgende Gerätetypen im Programm implementiert:
Folgende Parameter sind zur Beschreibung der Struktur des Universalschmiersystems erforderlich:
| NTa | Anzahl der Schmiertaschen. Die Schmiertaschen sind durchnummeriert mit JTa=1 bis NTa. |
| NPu | Anzahl der Schmiermittelversorgungspumpen. Die Pumpen sind durchnummeriert mit JPu=1 bis NPu. |
| NVe | Anzahl der Verbindungsleitungen. Die Verbindungsleitungen sind durchnummeriert mit JVe=1 bis NVe. |
| NVar | Anzahl der Gerätevarianten. Die Gerätevarianten sind durchnummeriert mit JVar=1 bis NVar. |
Zur Beschreibung der Zuordnung der Pumpen, der Schmiertaschen und der Gerätevarianten zu den einzelnen Verbindungsleitungen wird eine Verbindungsmatrix Ve(3,NVe) eingeführt, deren Felder die Nummern der jeweils zugeordneten Elemente enthalten.
Die Komponente Ve(1,JVe) =JPu(JVe) enthält dementsprechend die Nummer JPu der Pumpe, die mit der Verbindungsleitung Nr. JVe verbunden ist.
Die Komponente Ve(2,JVe) =JTa(JVe) enthält dementsprechend die Nummer JTa der Schmiertasche, die mit der Verbindungsleitung Nr. JVe verbunden ist.
Die Komponente Ve(3,JVe) =JVar(JVe) enthält dementsprechend die Nummer JVar der Gerätevariante, die in der Verbindungsleitung Nr. JVe angeordnet ist.
Im externen Universal-Schmiermittel-Versorgungssystem wird nicht mit einem Schmiermittel-Gas-Gemisch gerechnet. Es wird angenommen, dass alle Verbindungsleitungen stets vollständig mit Flüssigkeit gefüllt sind und keine Kavitation auftritt.
Zur Modellierung eines Schmiermittel-Versorgungssystem im Rahmen der Dateneingabe siehe die ausführlichen Beschreibungen in der Bedienanleitung im Abschnitt 4.4.9
zurück weiter zur dimensionslosen DarstellungAls Schmiermittelpumpen werden Konstantpumpen angenommen, die mit einem Druckbegrenzungsventil versehen sind. Damit ergibt sich für diese Pumpen eine Betriebskennlinie gemäß Bild 2.071.
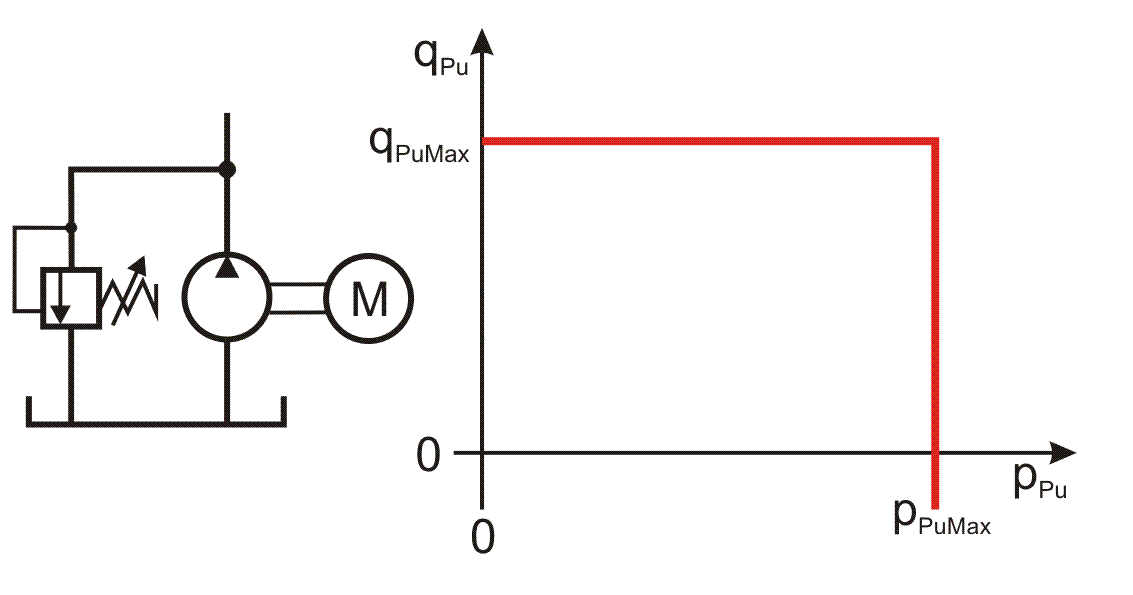
Bild 2.071: Betriebskennlinie einer Schmiermittelpumpe
Der Druck pPu ist der Ausgangsdruck, gegen den die Pumpe aktuell fördert. Der Ölstrom qPu ist der aktuelle Ölstrom den die Pumpe in eine oder verteilt auf mehrere Verbindungsleitungen in das Lager pumpt. Solange der maximal zulässige Pumpendruck pPuMax größer ist als der Gegendruck pPu aus den angeschlossenen Verbindungsleitungen, fördert die Pumpe den maximalen Ölstrom qPuMax in das Lager. Wenn der Gegendruck den maximalen Pumpendruck erreicht hat, lässt das Druckbegrenzungsventil den Druck nicht weiter ansteigen, in dem es einen Teil des Ölstroms ableitet, so dass der Ölstrom qPu kleiner wird als der maximale Pumpenstrom qPuMax. So verhält sich die Pumpe auf dem Ast qPu=qPuMax wie eine Konstantpumpe und auf dem Ast pPu=pPuMax wie eine druckgeregelte Pumpe. Es können damit also auch echte druckgeregelte Pumpen abgebildet werden.
Sollte der Druck in einer Schmiertasche, z.B. durch einen plötzlichen Lastanstieg im Lager, größer werden als der maximal zulässige Pumpendruck pPuMax und in der angeschlossenen Verbindungsleitung gibt es kein Rückschlagventil, dann könnte auch Schmiermittel in der Verbindungsleitung zurückfliesen, damit würde der aktuelle Pumpenölstrom qPu einen negativen Wert annehmen. Technisch bedeutet das, dass über das Druckbegrenzungsventil nicht nur der gesamte Pumpenölstrom qPuMax abfließt, sondern zusätzlich der Ölstrom der aus dem Lager kommt. In diesem Fall würde der aktuelle Pumpenölstrom qPu negativ werde, was also auch ein realistischer Fall sein kann.
Ein negativer aktueller Pumpendruck pPu ist dagegen nicht möglich, da durch die verwendeten Modelle der hydrodynamischen Schmierung verhindert wird, dass im Schmierspalt und damit auch in den Schmiertaschen negative Drücke berechnet werden. Der angegebene Pumpendruck wird üblicher Weise als absoluter Druck angegeben, das heißt, der Nullpunkt ist das absolute Vakuum. Das ist insbesondere bei der Verwendung der erweiterten Reynoldsschen Gleichung von Bedeutung, da diese im sich erweiternden Schmierspalt auch Kavitation simuliert.
Eine interessante Variante der hydrostatischen Schmiermittel-Versorgung ist ein volumetrischer Gleichverteiler (Bild 2.072), da dieser sehr energiesparend arbeitet.
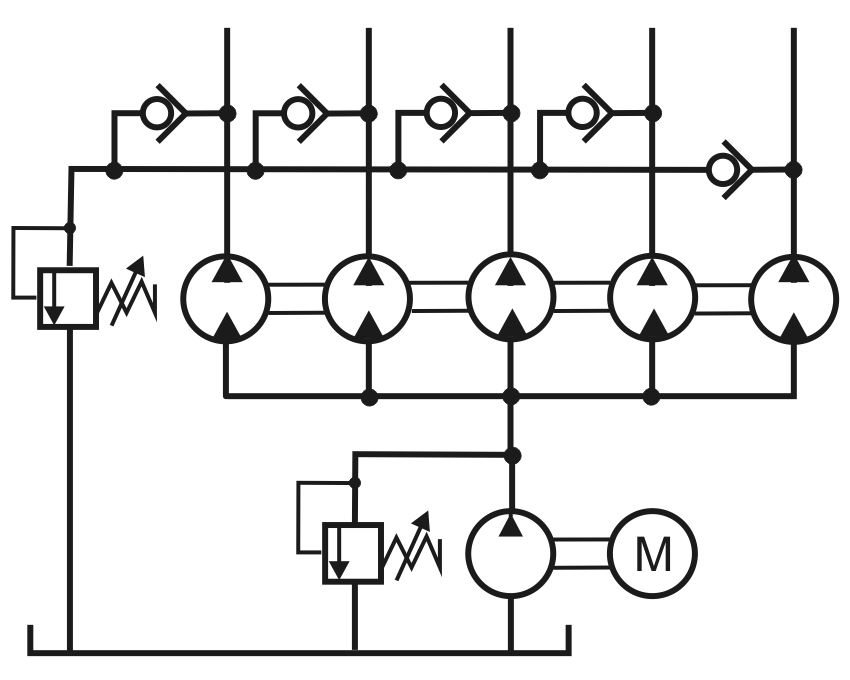
Bild 2.072: Volumetrischer Gleichverteiler
Dieser kann für seine Abbildung im Programm SIRUS einfach durch eine Reihe voneinander unabhängiger Konstantpumpen simuliert werde. Deshalb ist es nicht nötig, diese Variante extra zu implementieren. Lediglich den Druck, mit dem dieser volumetrische Gleichverteiler durch eine einzelne Pumpe dann versorgt wird, und die zu installierende Leistung der Pumpe, die den Gleichverteiler versorgt, muss nach der Simulation dieses Lagers über die Energiebilanz manuell ausgerechnet werden.
zurück weiter zur dimensionslosen DarstellungNachfolgend werden die Gerätetypen beschrieben, die in den Verbindungsleitungen angeordnet werden können.
zurück weiter zur dimensionslosen DarstellungDie klassische Form der hydrostatischen Schmiermittelversorgung ist die Anordnung von je einer Kapillare zwischen den Schmiertaschen und einer zentralen Schmiermittelpumpe.
Die Strömung in den Kapillaren kann als laminar angenommen werden. Dann ist der Ölstrom qVe der durch die Kapillare fließt abhängig vom Strömungswiderstand rcp der Kapillare und dem Druckverlust pVeVer zwischen Pumpendruck pPu und Schmiertaschendruck pTa. Es gilt also

Für eine Kapillare mit kreisrundem Querschnitt mit dem Durchmesser dcp und der Länge lcp lässt sich der laminare Strömungswiderstand rcp berechnen nach dem Gesetz von Hagen-Poiseuille [6, S.139] durch
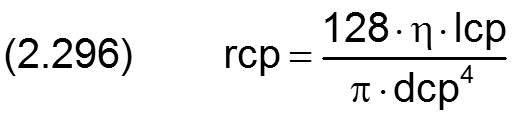
Dieser laminare Widerstand lässt sich aufspalten in die Viskosität η und eine Widerstandsbeiwert ccp der ausschließlich von der Geometrie der Kapillare abhängt. Es ist dann

und
![]()
Damit lässt sich die Gleichung für die Berechnung des Schmiermittelstroms qVe durch eine Kapillare in der Form angeben
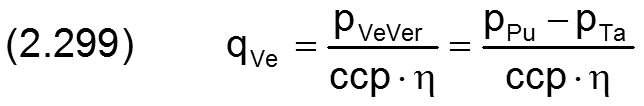
Diese Gleichung gilt auch allgemein für Laminardrosseln mit beliebiger Form des Querschnitts und auch für Rohrleitungswiderstände, sofern eine laminare Strömung über die gesamte Leitung angenommen werden kann. Es muss nur der entsprechende Widerstandsbeiwert ccp ermittelt werden, der nur von der Geometrie abhängt und nicht mehr von der Viskosität. Da zur Berechnung von Gleitlagern die Viskosität als ein wichtiger Parameter ohnehin bereits gegeben sein muss, ist der Widerstandsbeiwert ccp der einzige Parameter, der zur Beschreibung einer Kapillare bzw. eines laminaren Leitungswiderstandes angegeben werden muss.

Bild 2.073: Betriebskennlinie einer Laminardrossel, ohne Rückschlagventil links, mit Rückschlagventil rechts
Bild 2.073 zeigt die Kennlinien einer Laminardrossel mit und ohne Rückschlagventil. Es wird der Ölstrom qVe durch die Verbindungsleitung in Abhängigkeit vom Schmiertaschendruck pTa dargestellt bei einem vorgegebenen Pumpendruck pPu. Gemäß Definition pVeVer=pPu-pTa fließen positive Ölströme von der Pumpe in Richtung Schmiertasche. Sofern die Drossel nicht mit einem Rückschlagventil in Reihe geschaltet ist, können auch negative Ölströme auftreten (Kennlinie links), wenn der Schmiertaschendruck größer wird als der Pumpendruck.
Bild 2.074 zeigt nun noch die linearen Abhängigkeiten der Kennlinie des Ölstroms vom Pumpendruck pPu (links) und von der dynamischen Viskosität η rechts.
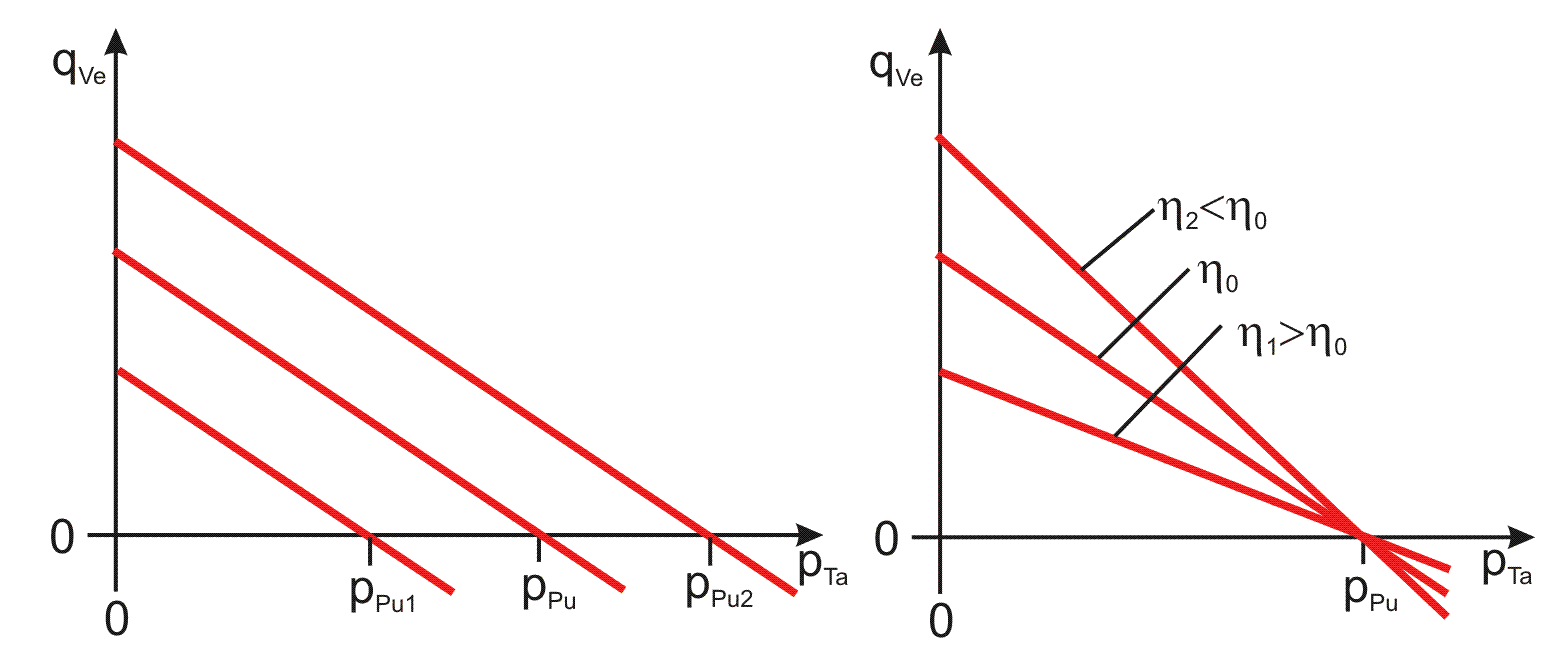
Bild 2.074: Kennfelder der Laminardrossel, Variation des Pumpendrucks pPu links, Variation der Viskosität η rechts
Die Verlustleistung in einer Laminardrossel, also die Leistung, die innerhalb der Drossel in Wärme umgewandelt wird, lässt sich berechnen durch
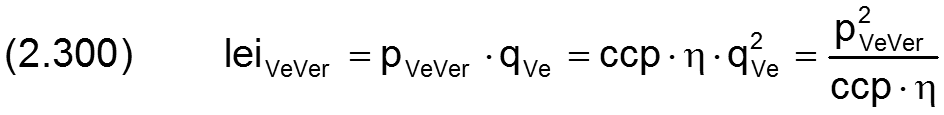
Eine hydrostatische Schmiermittelversorgung kann auch mittels Spaltdrosseln geregelt werden. Der Ölstrom qVe durch eine kreisrunde Spaltdrossel kann berechnet werden durch die Gleichung [6, S.140]
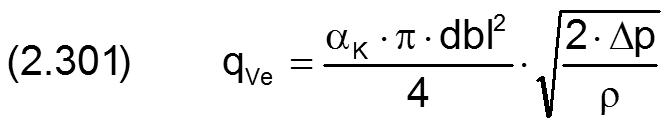
mit
| αK | Kontraktionszahl |
| dbl | lichter Durchmesser der Spaltdrossel (Blende) |
| ρ | Dichte der Schmierflüssigkeit |
| Δp | Druckverlust über die Spaltdrossel (Δp>/=0) |
Es kann ein Blendenbeiwert cbl definiert werden durch

"Die Kontraktionszahl αK hängt außer von der Einlaufgeometrie von der Strömungsgeschwindigkeit v1 ab und liegt im Bereich von αK = 0,6...1, bei scharfer Einlaufkante von 0,6 bis 0,64." [6, S.141] Nimmt man αK als konstanten Wert an, so ist auch cbl eine Konstante, die nur von der Geometrie der Blende abhängt. Das Programm SIRIUS arbeitet vereinfachend mit einem konstanten Blendenbeiwert cbl, der zuvor manuell berechnet oder durch Messung ermittelt werden muss.
Damit lässt sich die Gleichung (2.301) vereinfachen durch
![]()
Im Programm wird die Blende nur in Kombination mit einer in Reihe geschalteten Laminardrossel modelliert. Der Grund dafür ist, dass bei ausschließlicher Annahme einer Blende der Betrag der Steigung der Strom-Druck-Kennlinie gemäß Gleichung (2.302) bei p=0 unendlich groß wird, was zu numerischer Instabilität führt. Physikalisch erscheint es ebenfalls sinnvoll, auch immer einen gewissen laminaren Reibungswiderstand anzunehmen, da ja immer auch ein laminarer Widerstandsanteil anzunehmen ist in Form eines Reibungswiderstandes in der Zuleitung.
Die Kombination der Gleichungen (2.295) für die Laminardrossel und (2.303) für die Blende ergibt eine Strom-Druck-Kennlinie für eine Reihenschaltung von Laminardrossel und Spaltdrossel von
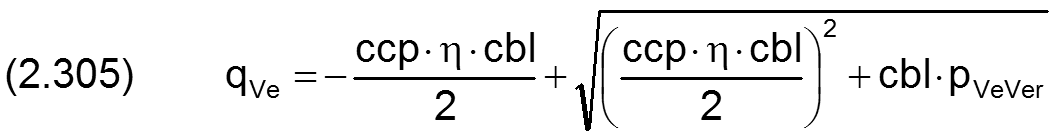 |
für pVeVer>/=0 |
| ccp | Widerstandsbeiwert des laminaren Strömungswiderstandes |
| cbl | Blendenbeiwert der Spaltdrossel |
| η | dynamische Viskosität der Schmierflüssigkeit |
| pVeVer | Druckverlust über die Drosseln pVeVer=pPu-pTa |
Wenn kein Rückschlagventil in der Schmiermittelleitung einen Rückfluss des Schmiermittels verhindert, gilt für den entsprechenden Rückstrom des Schmiermittels
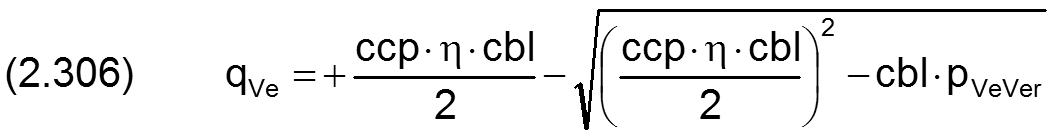 |
für pVeVer<0 |
Dabei wird vereinfachend angenommen, dass die Drosselwirkung der Spaltdrossel in beiden Stromrichtungen gleich ist.
Bild 2.075 zeigt die Kennlinie der Reihenschaltung einer Laminardrossel und einer Spaltdrossel. Es wird der Ölstrom qVe durch die Verbindungsleitung in Abhängigkeit vom Schmiertaschendruck pTa dargestellt bei einem vorgegebenen Pumpendruck pPu. Gemäß Definition pVeVer=pPu-pTa fließen positive Ölströme von der Pumpe in Richtung Schmiertasche und negative von der Schmiertasche in Richtung Pumpe.
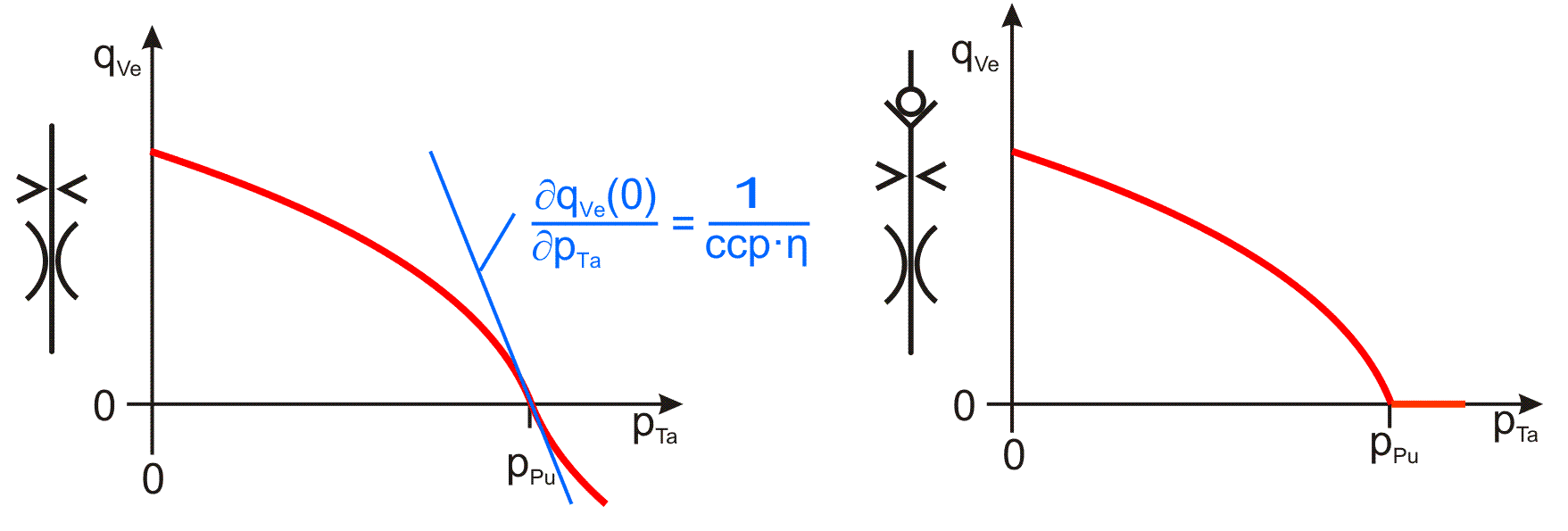
Bild 2.075: Betriebskennlinie einer Spaltdrossel in Reihe mit einer Laminardrossel, ohne Rückschlagventil links, mit Rückschlagventil rechts
Bild 2.076 zeigt nun noch die Abhängigkeiten der Kennlinie des Ölstroms vom Pumpendruck pPu (links) und von der dynamischen Viskosität η rechts.
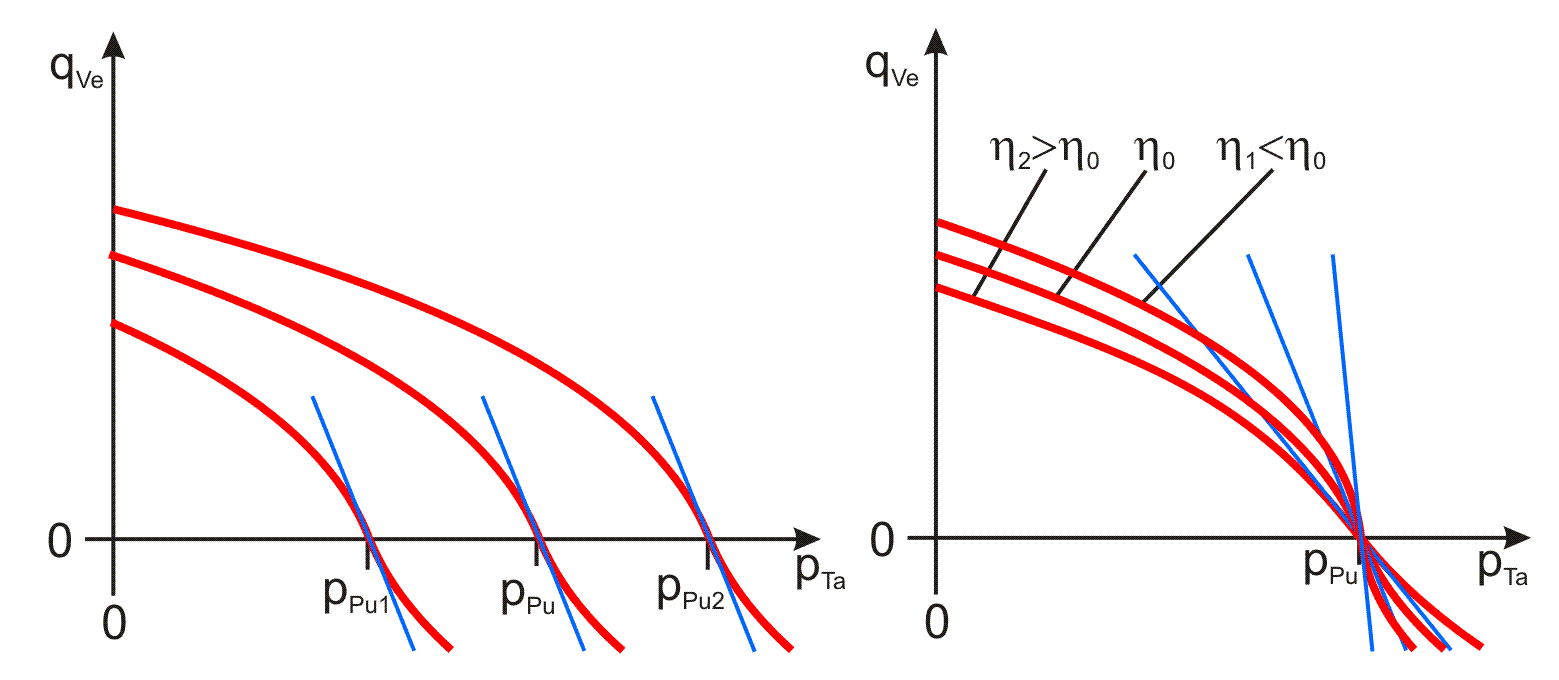
Bild 2.076: Kennfelder der Reihenschaltung von Spalt- und Laminardrossel, Variation des Pumpendrucks pPu links, Variation der Viskosität η rechts
Die Verlustleistung leiVeVer in einer Reihenschaltung von Spalt- und Laminardrossel, also die Leistung, die innerhalb der Drosseln in Wärme umgewandelt wird, lässt sich berechnen durch
![]()
Im Vergleich zu der Verwendung von einfachen Laminardrosseln für die Ölstrom-Verteilung im hydrostatischen Lager kann man durch den Einsatz von Progressiv-Mengen-Reglern (PM-Regler) der Firma Hyprostatik [36] den erforderlichen Ölstrom reduzieren und damit Energie einsparen.
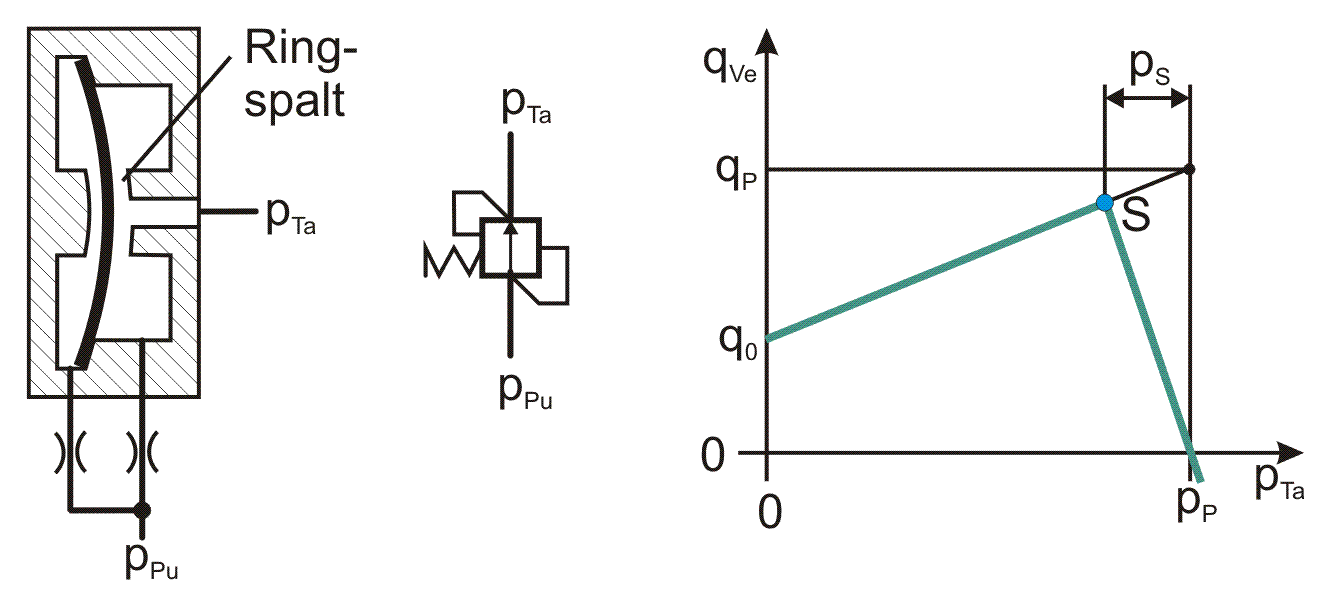
Bild 2.077: PM-Regler, prinzipieller Aufbau links, vereinfachtes Schaltsymbol Mitte, idealisierte Kennlinie rechts
Bild 2.077 zeigt links den prinzipiellen Aufbau dieses Reglers. Eine elastische Membran, die von beiden Seiten mit Druck beaufschlagt wird, verstellt die Spalthöhe eines Ringspalts, verändert damit den Drosselwiderstand dieses Ringspalts und regelt so den Ölstrom. Damit stellt dieses Ventil ein Druckdifferenzventil (Druckwaage) dar, da der Drosselwiderstand im Wesentlichen durch die Druckdifferenz zwischen Eingangs- und Ausgangsdruck geregelt wird. Der Hersteller gibt für den PM-Regler eine idealisierte Kennlinie an (Bild 2.077, rechts), die mit den 4 Kennwerten pP, q0, qP, pS konstruiert werden kann. Dabei sind
| η0 | dynamische Viskosität während der Aufnahme der Kennlinie (vermutlich die Eingangsviskosität) |
| pP | Pumpendruck (während der Aufnahme der Kennlinie) |
| q0(pP,η0) | Ölstrom bei Schmiertaschendruck pTa=0, Pumpendruck pPu=pP und dynamischer Viskosität η=η0 |
| qP(η0) | theoretischer Ölstrom bei Taschendruck pTa=pP und dynamischer Viskosität η=η0. Der Wert qP ist die Ordinate des Schnittpunktes der Verlängerung des aufsteigenden Hauptastes der Kennlinie mit der senkrechten Linie durch den Wert pP auf der Abszisse des Diagramms. |
| pS | Druckdifferenz zwischen dem Pumpendruck pP und der Stelle S des maximalen Ölstroms |
Damit sind 5 Kennwerte ausreichend, um die Funktionsweise des PM-Reglers vereinfacht zu beschreiben.
Da der PM-Regler ein Druckdifferenzventil ist, verschiebt sich die Kennlinie bei Veränderung des Pumpendruckes gemäß Bild 2.078.
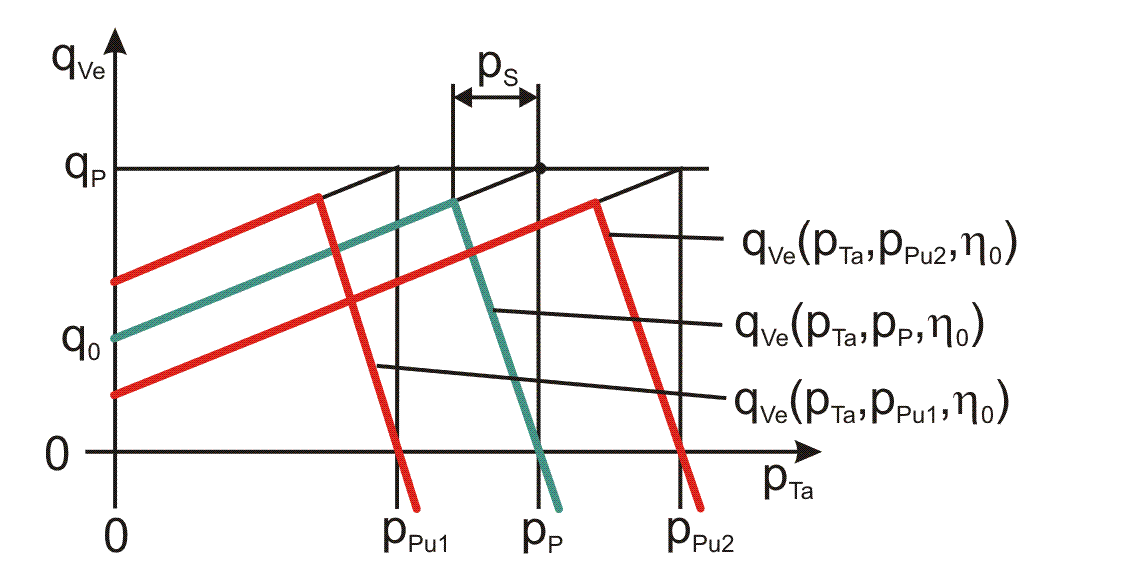
Bild 2.078: Kennfeld des PM-Reglers für verschiedene Pumpendrücke pPu
Gemäß der Annahme, dass alle Widerstände im PM-Regler im Wesentlichen auf laminarer Strömung beruhen, gibt der Hersteller für die Umrechnung der Ölströme auf verschiedene Viskositäten eine einfache proportionale Umrechnung an
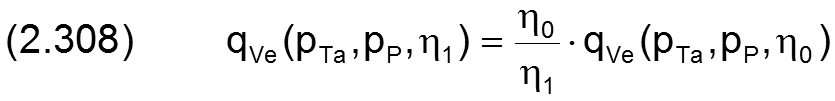
Bild 2.079 zeigt die Kennlinien für verschiedene Viskositäten.
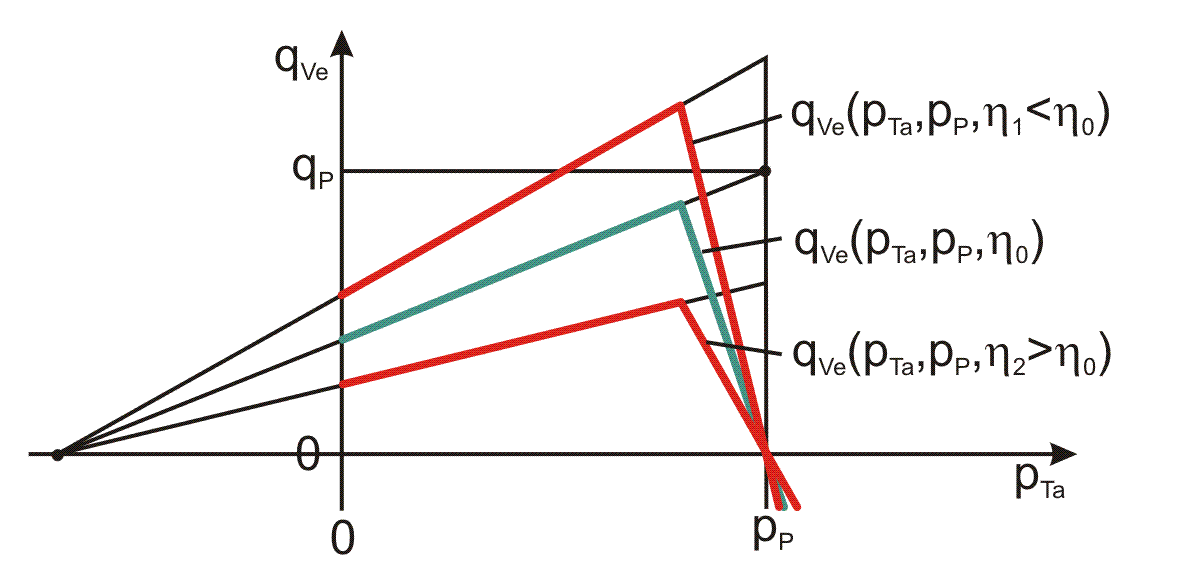
Bild 2.079: Kennfeld des PM-Reglers für verschiedene Viskositäten η
Aus den 5 Kennwerten der Standardkennlinie eines PM-Reglers können die Parameter für die Kennlinie qVe(pTa,pPu,η1) für einen beliebigen Pumpendruck pPu und eine beliebige dynamische Viskosität η1 berechnet werden, die SIRIUS für die Simulation des PM-Reglers benutzt. Bild 2.080 zeigt die Standardkennlinie mit den Angaben des Herstellers und eine umgerechnete Kennlinie. Da die umgerechnete Kennlinie bei der Wahl eines wesentlich höheren Pumpendruckes als pP so weit nach rechts verschoben werden kann, dass der aufsteigende Ast die Abszisse bereits bei einem Taschendruck pTa>0 schneidet, wird die Kennlinie links dieses Punkte vorsorglich um den Ast qVe(pTa)=0 verlängert.
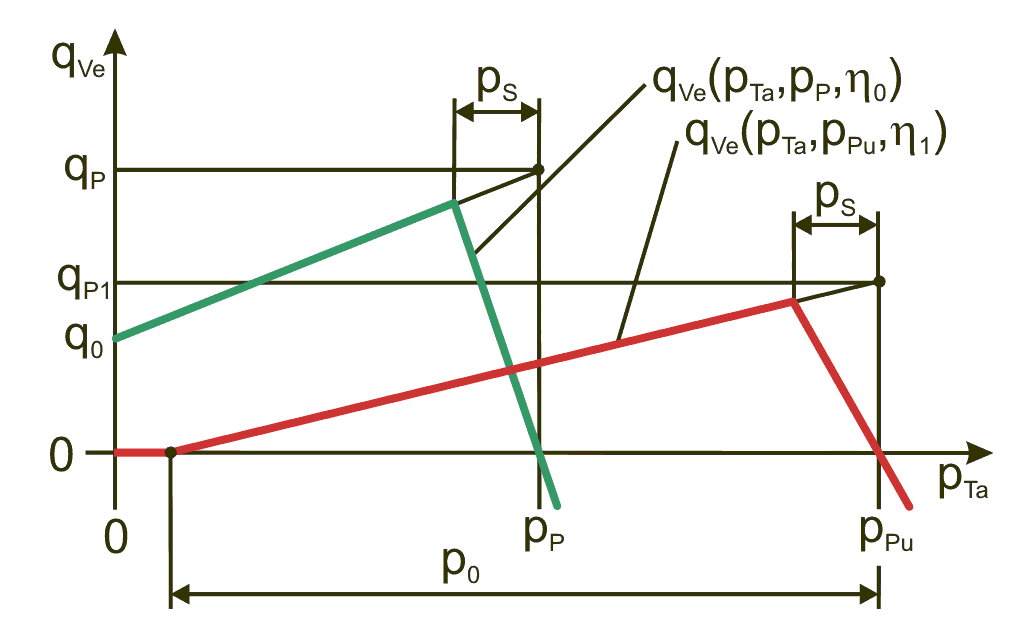
Bild 2.080: Standardkennlinie grün und umgerechnete und erweiterte Kennlinie rot
Der neue theoretische Ölstrom qP1 des aufsteigenden Astes der Kennlinie bei pTa=pPu wird gemäß Gleichung (2.308) berechnet durch
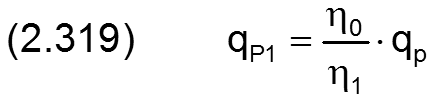
Die Steigung cpm des aufsteigenden Astes der umgerechneten Kennlinie ist gegeben durch

Die Steigung -rpm des absteigenden Astes der Kennlinie ist gegeben durch
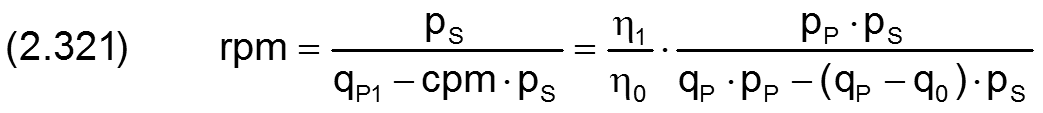
Der Parameter rpm ist auch der laminare Widerstand des PM-Reglers im maximal geöffnetem Zustand.
Der Abstand p0 des linken Nullpunktes der Kennlinie vom Pumpendruck pPu wird berechnet durch
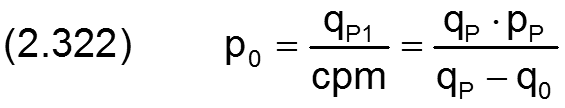
Der linke Ast der Kennlinie wird nur wirksam, wenn pPu-p0>0 ist. Er ist eigentlich nur dazu eingerichtet, damit das Lagerprogramm unter extremen Bedingungen keinen all zu großen Unsinn rechnet und sollte möglichst nicht wirksam werden. Wenn der Ölstrom bei Taschendruck pTa=0 gegen Null geht, neigt die Regelstrecke der hydrostatischen Schmiermittelversorgung auch zu instabilem Verhalten.
Mit diesen Parametern kann die idealisierte Kennlinie des PM-Reglers ohne Rückschlagventil für beliebigen Pumpendruck pPu und beliebige Viskosität η1 angegeben werden durch

Werden in der Verbindungsleitung ein PM-Regler und ein Rückschlagventil in Reihe geschaltet, dann ist die Gleichung für die Kennlinie um einen rechten Ast, ab pTa>pPu zu erweitern. Damit ist die Kennlinie für diesen Fall gegeben durch
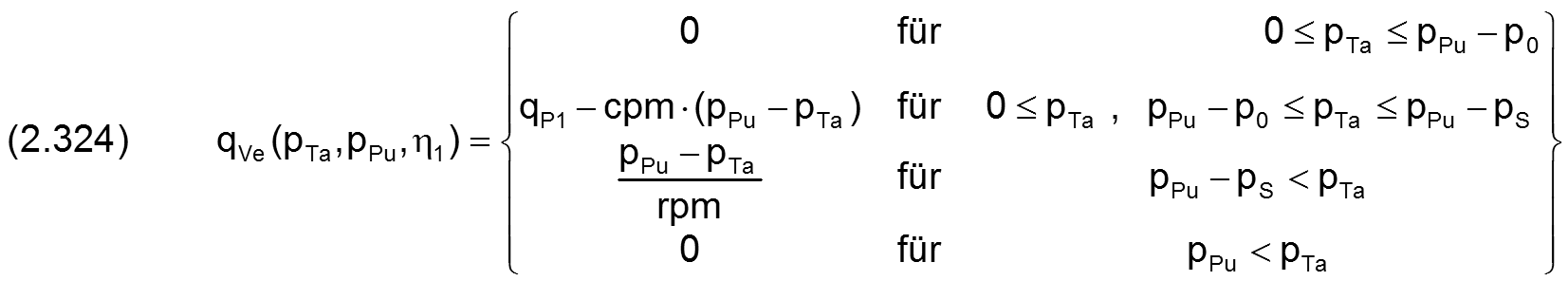
Bei einem Druckverlust pVeVer = pPu - pTa ist die Verlustleistung leiVeVer im PM-Regler analog der Laminardrossel gegeben durch
![]()
Mit den Formeln für die einzelnen Äste der Kennlinie z.B. für den PM-Regler ohne Rückschlagventil gemäß Gleichung (2.323) lässt sich die Gleichung für die Verlustleistung im Regler weiter konkretisieren

Weitere Informationen über die Funktionsweise der PM-Regler sind auch nachzulesen unter [19].
Das Universal-Schmiersystem stellt ein einfaches Netzwerk dar, mit mehreren Knoten, an denen die Schmiermittelströme verzweigen. Um die Verteilung der Schmiermittelströme der Pumpen auf die einzelnen Verbindungsleitungen und dann auf die einzelnen Schmiertaschen richtig zu berechnen, muss für jeden Knoten die Volumenbilanz aufgestellt werden. Jeder Eingang der NTa Schmiertaschen ist ein Knoten des Netzwerks, da jede Schmiertasche mit mehreren Verbindungsleitungen verbunden sein kann. Jeder Pumpenausgang ist ebenfalls ein Knoten, da von jeder Pumpe mehrere Verbindungsleitungen ausgehen können.
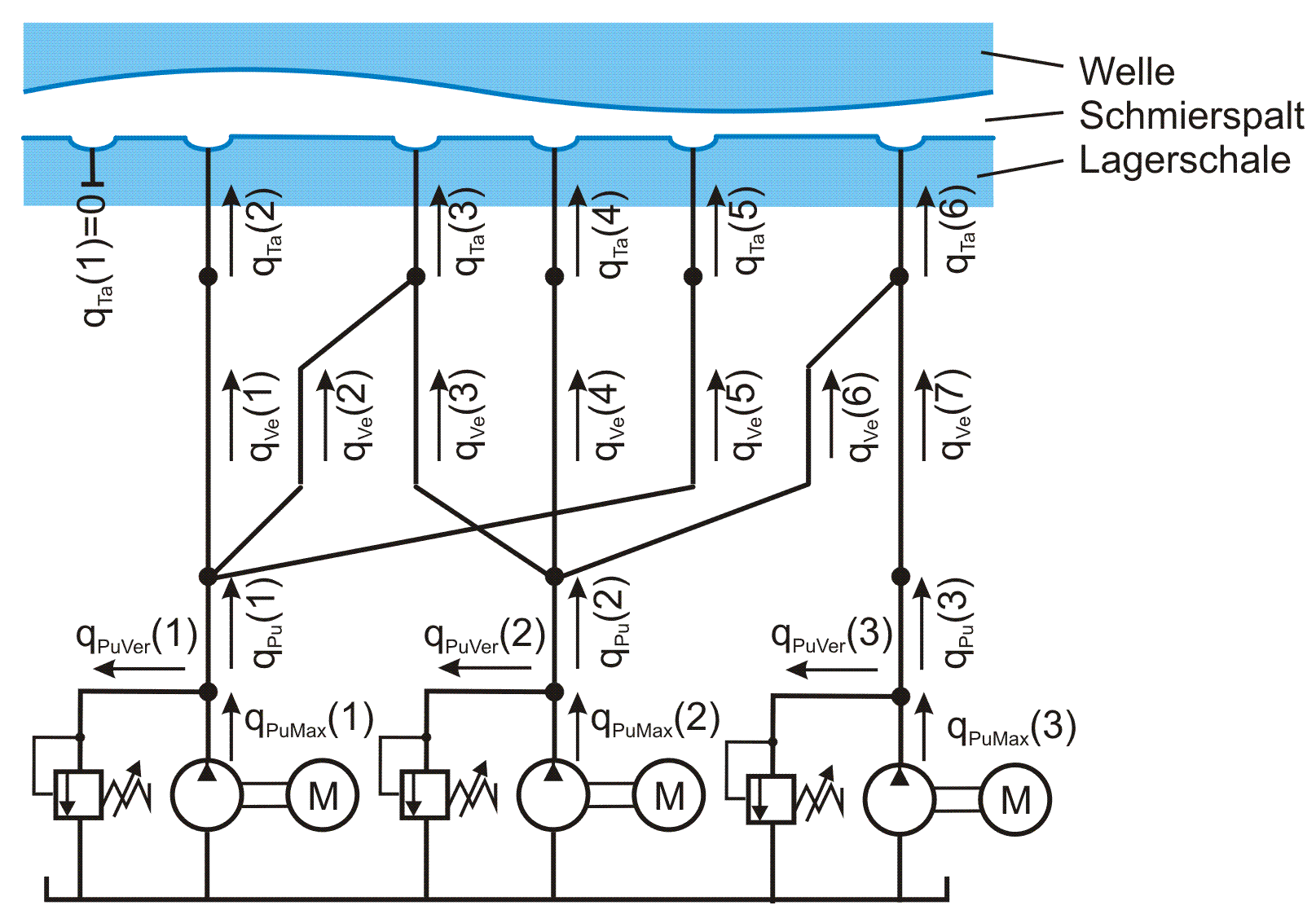
Bild 2.081: Schmiermittelströme im peripheren Schmiersystem
Bild 2.081 zeigt die Netzstruktur einer möglichen Variante des Schmiersystem und die Bezeichnungen der einzelnen Teilströme. Schmiermittelströme, die von den Pumpen weg gerichtet sind, haben ein positives Vorzeichen.
Für die Pumpen Nr. JPu = 1 bis NPu, die ihren Schmiermittelstrom qPu(JPu) auf einige der NVe Leitungen mit den Ölströmen qVe(JVe) für JVe=1 bis NVe verteilen, gelten die Ölstrombilanzen

Analog zu Formel (2.330) wird auch die Bilanz der Schmiermittelströme an den Schmiertascheneingängen aufgestellt
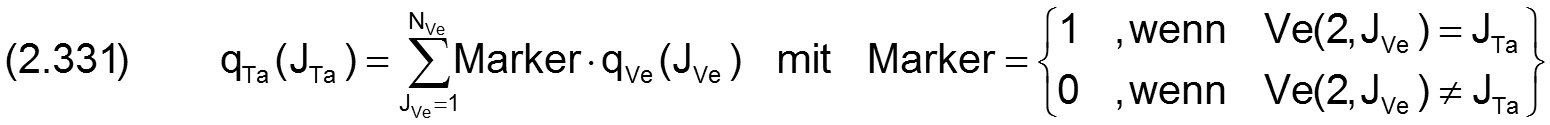
Für den Gesamtölstrom des peripheren Schmiersystems in Richtung Schmierspalt kann nun folgende Beziehung aufgestellt werden.
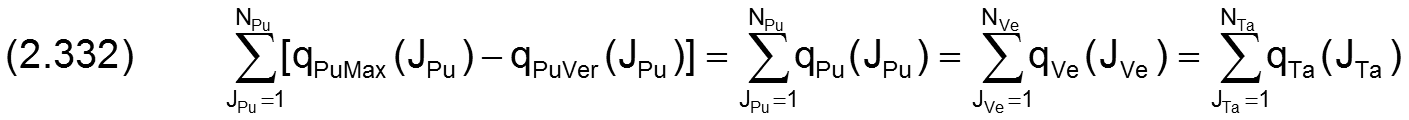
Die installierte Gesamtausgangsleistung aller Pumpen des peripheren Schmiersystem ist gegeben durch

Diese Leistung wird in der Regel aber nicht vollständig abgerufen, da nicht immer der maximale Pumpendruck anliegt.
Die von den Pumpen tatsächlich bereitgestellte Ausgangsleistung, die dann auch Energiekosten verursacht, ist gegeben durch
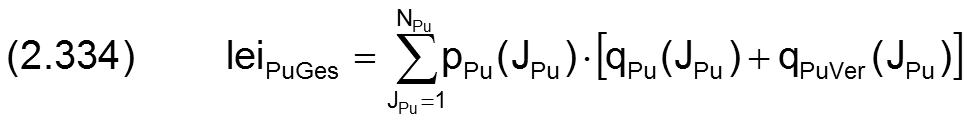
Diese Leistung muss nicht vollständig in die Verbindungsleitungen zu den Schmiertaschen eingespeist werden. Einige Pumpen, die aufgrund eines hohen Gegendrucks an den Eingängen der Verbindungsleitung ihren Maximaldruck erreicht haben, leiten als Konstantpumpen den überschüssigen Ölstrom über das Druckbegrenzungsventil ab, so das bereits an den Pumpenaggregaten die Verlustleistung leiPuVerGes entstehen kann

Diese Verlustleistung braucht nicht berücksichtigt werden, wenn die Schmiermittelpumpen Regelpumpen sind, die bei Druckstößen ausreichend schnell reagieren bzw. mit einem Speicher gepuffert sind.
Die Summe der Leistungen, die in die Verbindungsleitungen zur Versorgung der Schmiertaschen eingespeist wird, ist nun gegeben durch
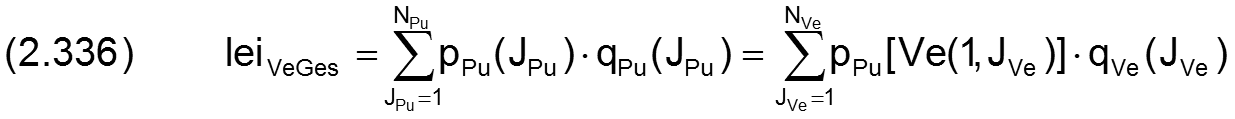
Von dieser Leistung wird durch die Widerstände in den Verbindungsleitungen und den Stromregelgeräten ein weiterer oft recht großer Anteil in Wärme umgewandelt. Die Summe leiVeVerGes der Verlustleistungen in den Verbindungsleitungen ist gegeben durch
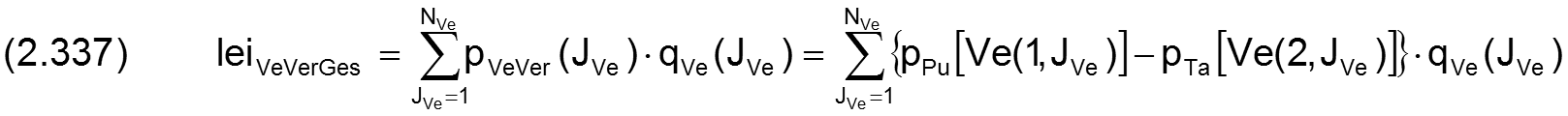
Die Restleistung leiTaGes, die dann über die Schmiertaschen dem Schmierspalt zugeführt wird, ist gegeben durch

Damit lässt sich die Energiebilanz für das gesamte periphere Schmiermittel-Versorgungssystem aufstellen
![]()
.
.
.