Die dimensionsbehaftete Darstellung beschreibt die Sachverhalte und Gleichungen in gewohnter Weise mit physikalischen Größengleichungen. Programmintern wurden diese Gleichungen zwar generell nicht verwendet, sie sind aber die Grundlage für die Ableitung der dimensionslosen Gleichungen, die im Abschnitt 2.2 dargestellt sind und für die Programmierung generell verwendet wurden.
zurück weiter zur dimensionslosen DarstellungGegenstand der Berechnung und der Simulation des Programms SIRIUS sind hydrodynamisch und hydrostatisch geschmierte Radialgleitlager. Wenn nachfolgend von einem Gleitlager oder einem Lager die Rede ist, ist regelmäßig ein hydrodynamisch und/oder hydrostatisch geschmiertes Radialgleitlager gemeint.
Das Lager besteht aus einer Lagerschale und einer sich darin drehenden Welle bzw. Achse. Nachfolgend wird dafür nur noch der Begriff Welle verwendet. Wenn von Achsen die Rede ist, sind Rotations-, Symmetrie- oder Koordinatenachsen gemeint.
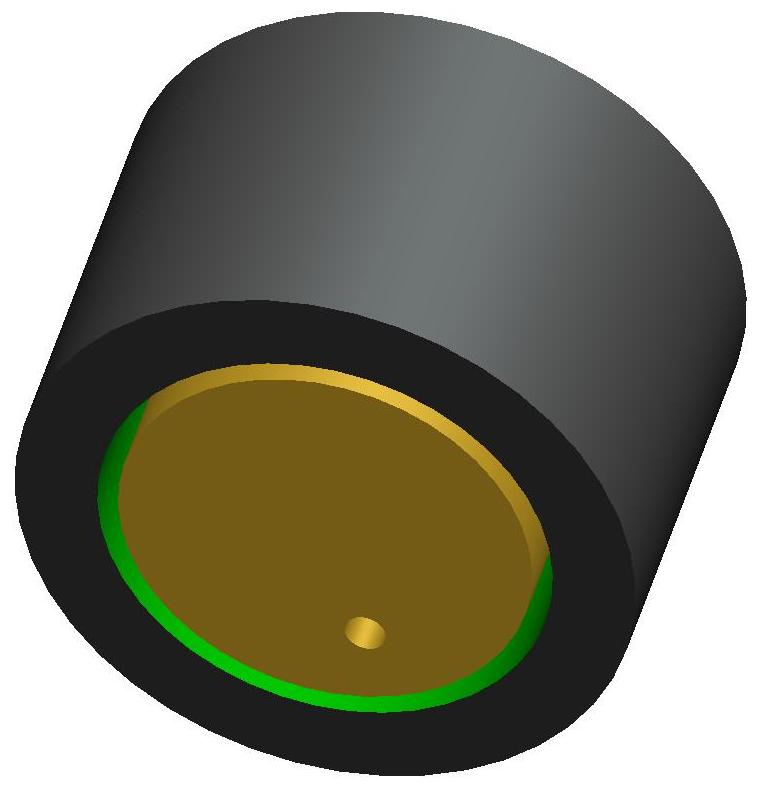
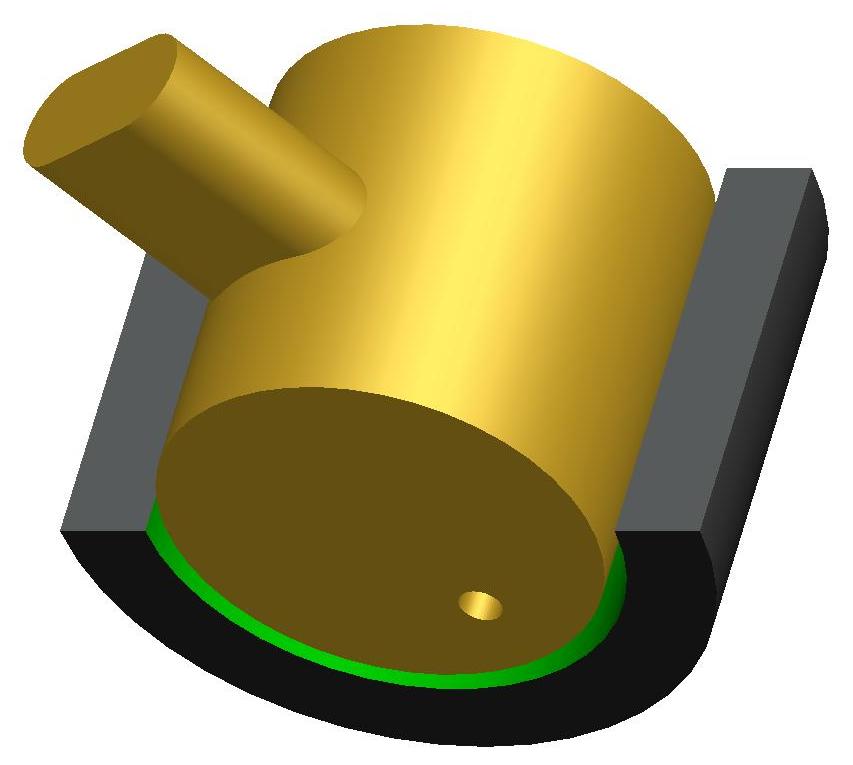
Aufgabe eines Radialgleitlagers ist die möglichst verschleißfreie Übertragung der Kräfte von einer Welle auf die Lagerschale bei gleichzeitiger Rotation der Welle relativ zur Lagerschale. Es können voll umschlossene Lager simuliert werden (Bild 2.001 links), als auch teilweise umschlossene Lager (Bild 2.001 rechts).
 |
 |
Die drei geometrischen Hauptmaße eines Radialgleitlagers sind der Nenndurchmesser d, die Lagerbreite b und das Lagerspiel s (Bild 2.002).
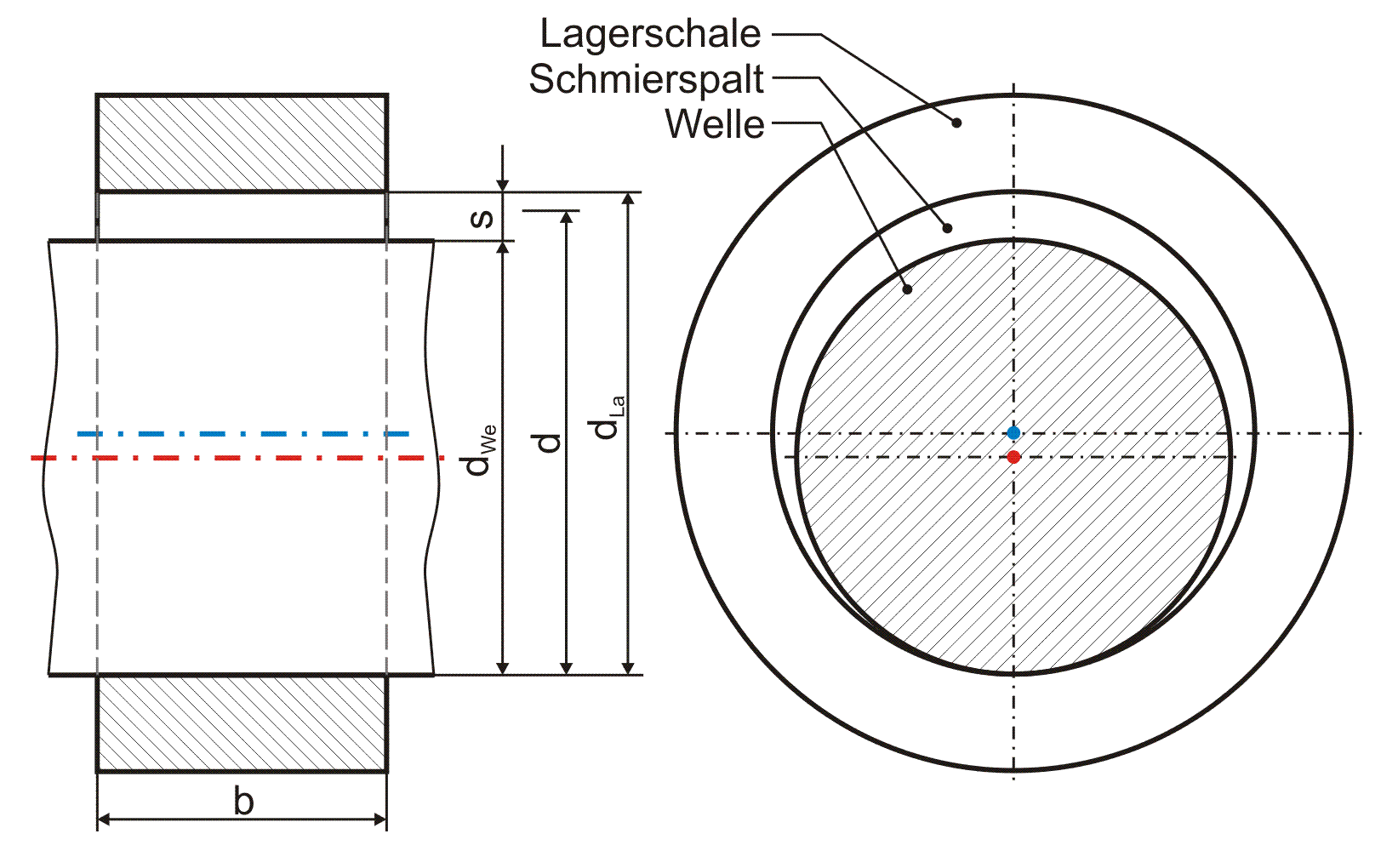
Bild 2.002: Hauptabmessungen eines Radiallagers
Das Lagerspiel ist gegeben durch die Differenz von Lagerschalen-Innendurchmesser dLa und Wellendurchmesser dWe mit
![]()
Es liegt üblicher Weise im Bereich um 1 ‰ des Nenndurchmessers des Lagers.
In der Lagertheorie werden viele Parameter auf diesen Durchmesser bezogen. Da das Lagerspiel so klein ist, ist es meist unerheblich, ob man für diesen Bezugsdurchmesser d den exakten Wellendurchmesser, den exakten Lagerschalen-Innendurchmesser oder einen gerundeten Wert in der Nähe verwendet. Deshalb spricht man üblicher Weise vom Lagerdurchmesser d, oder auch vom Wellendurchmesser d, und meint damit den Nenndurchmesser.
zurück weiter zur dimensionslosen DarstellungZur eindeutigen Beschreibung der Lagerparameter sind im Lager zwei lagerschalenfeste Koordinatensysteme definiert.
Der Ursprung des kartesische Koordinatensystems 1-2-3 liegt in der Mitte der Lagerschale. Die Achse 1 ist horizontal ausgerichtet. Die Achse 2 zeigt nach Unten und entspricht damit der Hauptlastrichtung (Äußere Kraft auf die Welle bzw. Kraft der Wellenoberfläche auf den Schmierfilm). Die Achse 3 fluchtet mit der Achse der Lagerschale. (Bild 2.003)

Bild 2.003: Lagerschalenfeste Koordinatensysteme in einem teilweise umschlossenen Lager
Ein zweites Koordinatensystem x-y-z ist entlang der zylindrischen Gleitfläche der Lagerschale angeordnet. Die x-Achse verläuft in Umfangsrichtung. Die y-Achse zeigt hin zur Lagerachse und die z-Achse zeigt in axiale Richtung, entgegengesetzt zur Achse 3 des Koordinatensystems 1-2-3. Der Ursprung des x-y-z-Koordinatensystems liegt im Schnittpunkt der positiven Achse 2 des Koordinatensystems 1-2-3 und der Lagerschalengleitfläche.
Falls Formabweichungen der Lagerschale von der ideal zylindrischen Form angenommen werden, liegt der Ursprung des Koordinatensystems x-y-z auf der Mantelfläche eines idealen Zylinders mit dem (mittleren) Schalendurchmesser dLa, von dem aus die Formabweichungen h der Lagerschalenoberfläche angegeben werden. Die z-Achse verläuft dann entlang der ideal zylindrischen Mantelfläche.
Beide Koordinatensysteme sind Rechtssysteme.
zurück weiter zur dimensionslosen DarstellungZur Herleitung der Reynoldsschen Differentialgleichung und zur übersichtlichen Darstellung der örtlichen Schmierspalt-Daten, z.B. der Schmierspalthöhe h(x,z) und/oder der Druckverteilung p(x,z) im Schmierspalt, wird die Spaltfläche oft in eine Ebene abgewickelt dargestellt gemäß Bild 2.004.
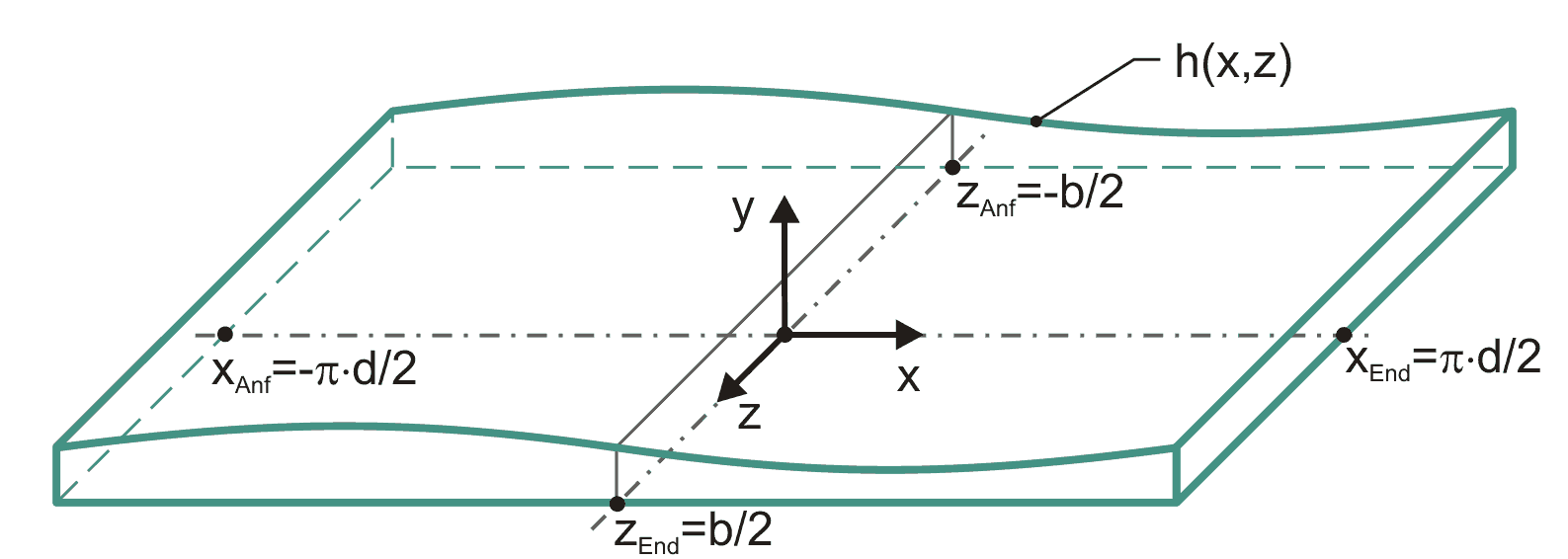
Bild 2.004: Abgewickelter Schmierspalt h(x,z) eines voll umschlossenen Lagers
So ist die Schmierspaltfläche darstellbar durch eine Rechteck der Breite zEnd-zAnf=b und der Länge xEnd-xAnf=π·d für ein voll umschlossenes Lager. Falls das Lager geometrisch und physikalisch symmetrisch ist, wird für die Berechnung nur der halbe Schmierspalt abgebildet gemäß Bild 2.005. Dann ist die abgebildete Lagerbreite nur noch zEnd-zAnf = b/2
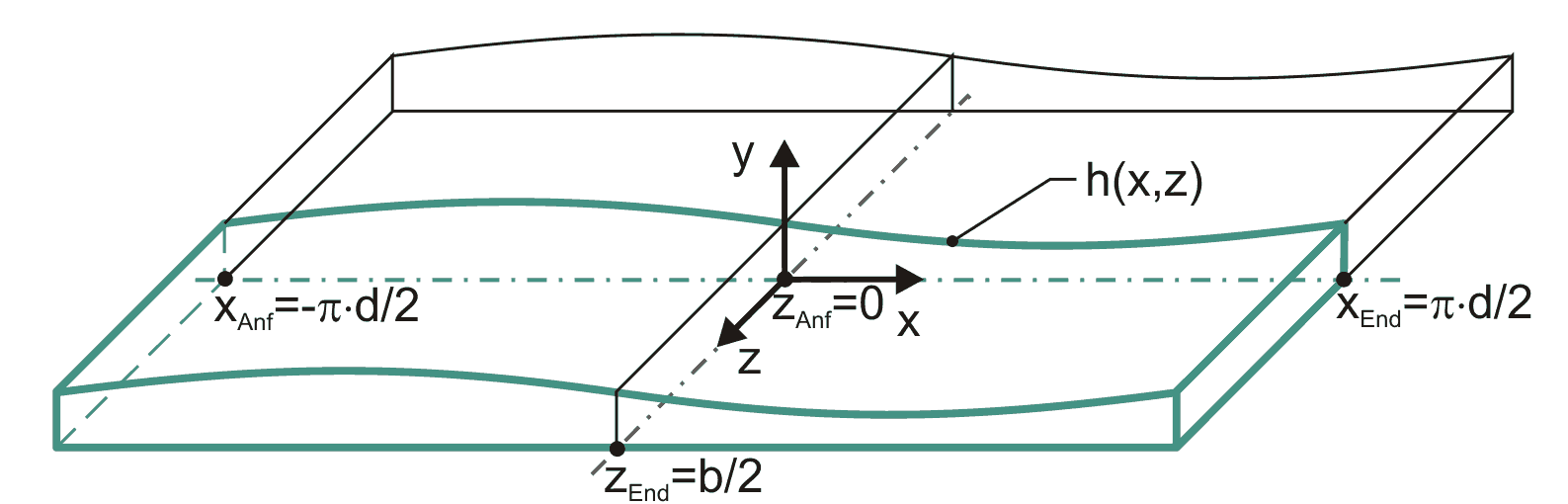
Bild 2.005: Abbildung des abgewickelten Schmierspalts h(x,z) eines symmetrischen voll umschlossenen Lagers (grüne Linien)
Im Programm SIRIUS sind gemäß Bild 2.004 bzw. Bild 2.005 die Ränder der abgewickelten Schmierspaltfläche bezogen auf das Koordinatensystem x-y-z gegeben durch
![]()
![]()
sowie für das voll umschlossene Lager
![]()
![]()
und für ein teilweise umschlossenes Lager
![]()
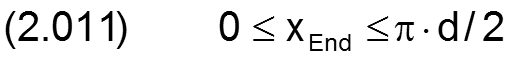
und
![]()
Der oben definierte Lagerparameter "Lagerspiel" s ist neben den Parametern zur Beschreibung der Wellenverlagerung in der Lagerschale ausreichend, um die Spaltgeometrie h(x,z,t) bei ideal zylindrischer Lagerschale und Welle zu beschreiben. Wenn man aber auch von der idealen Form abweichende Lager simulieren will, ist es hilfreich den Begriff des "Spielraums" einzuführen, der neben dem skalaren Parameter s noch durch weitere nachfolgend eingeführte Parameter beschrieben wird und in seiner grafischen Darstellung einen guten Überblick über die Verhältnisse im Lager gibt.
Durch den Spielraum erhält die Welle innerhalb der Lagerschale eine geringe radiale Bewegungsfreiheit. In einem Lager mit ideal zylindrischer Welle und ideal zylindrischer Lagerschale kann die Wellenachse gegenüber der Lagerschalenachse in alle radialen Richtungen einen maximalen Versatz von s/2 annehmen. Der Spielraum ist für das ideale Lager ein Zylinder mit dem Durchmesser s und der Länge b. In die grafische Darstellung des Spielraums mit einem stark vergrößert dargestellten Spiel s im Vergleich zur Lagerbreite b und der darin eingezeichneten Lage der Wellenachse lassen sich die aktuellen Verhältnisse in einem Lager sehr gut veranschaulichen. Bild 2.006 (links) zeigt eine Prinzipskizze des Spielraums mit der Achse der Lagerschale (blau) im Zentrum des Spielraums (grün) und einer möglichen Lage der Wellenachse (rot) entsprechend Bild 2.002, wenn das Lager außer Betrieb ist und die Welle unten in der Lagerschale liegt. Wie rechts im Bild zu sehen, kann dieser Spielraum auch durch das Programm SIRIUS mit Hilfe des Grafikprogramms Gnuplot dargestellt werden. Das ist besonders dann von Vorteil, wenn der Spielraum durch verschiedene Formabweichungen kein Zylinder mehr ist.
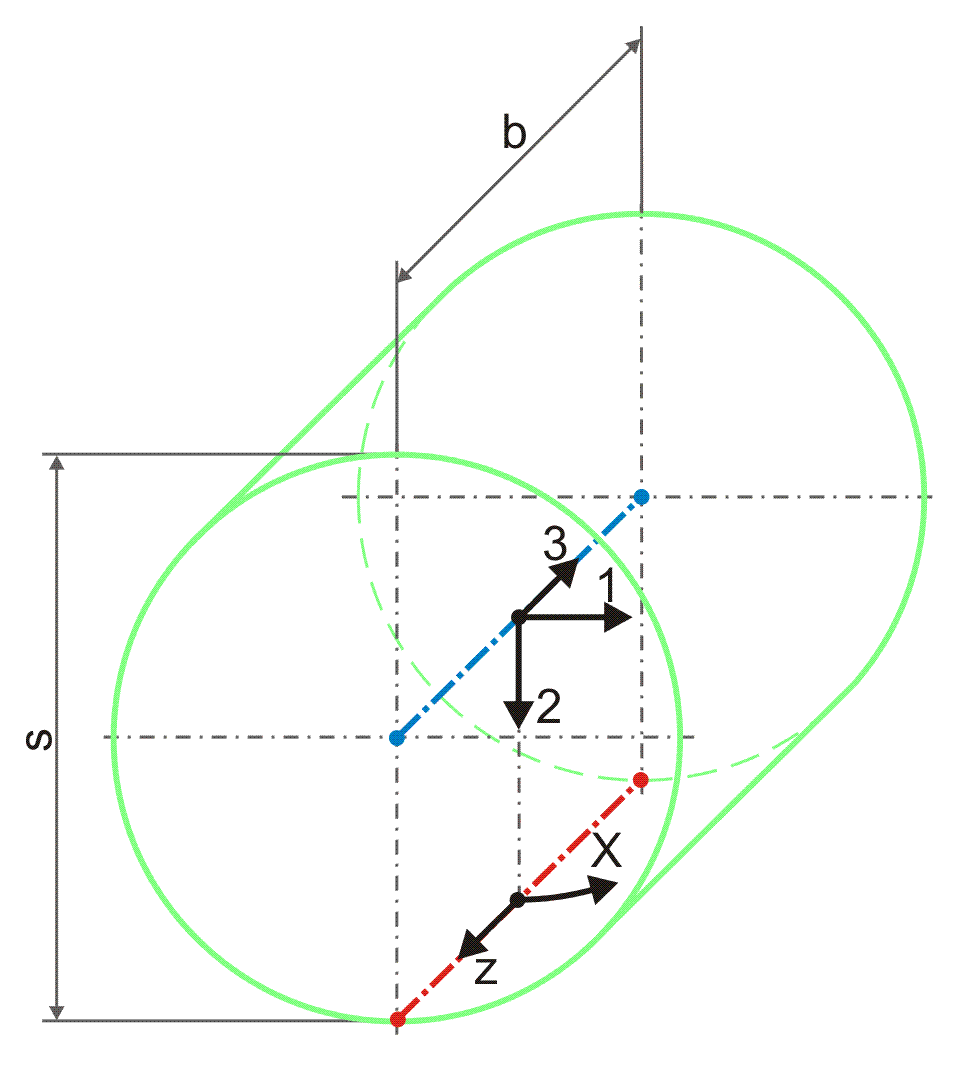 |
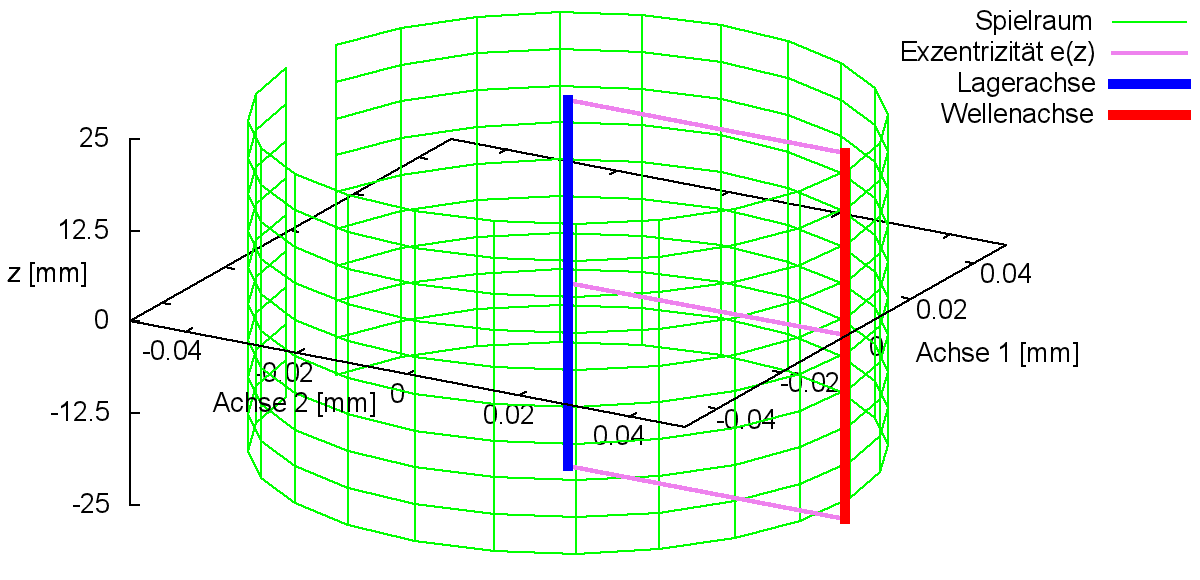 |
Durch diese Darstellung kann die Lage der Welle innerhalb der Lagerschale gut beurteilt werden. Berührt die Wellenachse die Mantelfläche des Spielraums, zeigt das den Festkörperkontakt zwischen Lagerschale und Welle an, was bei einem hydrodynamisch geschmierten Lager möglichst zu vermieden ist.
Für Lager mit beliebigen Spaltgeometrien lässt sich der Spielraum konstruieren, indem man zunächst ein Fluchten von Lagerschale und Welle annimmt und die sich dabei ergebenden Spalthöhen h(x,z) in Zylinderkoordinaten um die Wellenachse herum aufträgt. D.h., dass der Wellendurchmesser zu Null abstrahiert wird. Anschließend wird für den jeweiligen Lastfall die Lage der Wellenachse innerhalb dieses Spielraums eingetragen.
zurück weiter zur dimensionslosen DarstellungDie Relativbewegung zwischen der Wellenoberfläche und der Gleitfläche der Lagerschale ist eine wesentliche Voraussetzung für die Entstehung hydrodynamischer Schmierung, weil durch das an den Gleitflächen haftende zähe Schmiermittel eine Schleppströmung entsteht, die das Schmiermittel in den sich verengenden Schmierspalt pumpt.
Es wird angenommen, dass die Lagerschale fest steht und die Welle sich mit der Winkelgeschwindigkeit ω bzw. mit der Drehzahl n dreht. Das stellt keine Einschränkung in den Betriebsbedingungen dar, weil für das Lagerverhalten nur die Relativgeschwindigkeit zwischen Welle und Lagerschale von Interesse ist. Drehen sich beide Lagerteile, ist im Programm SIRIUS als Winkelgeschwindigkeit der Welle die Differenz beider Winkelgeschwindigkeiten anzusetzen.
HINWEIS: Beachte hierbei, das die Richtung XSo der Lagerbelastung immer bezogen auf das lagerschalenfeste Koordinatensystem x-y-z angegeben werden muss. So wird z.B. eine konstante Lagerbelastung bezogen auf eine rotierende Lagerschale zu einer umlaufenden d.h. instationären Lagerbelastung.
Im Programm SIRIUS können zeitlich konstante und variable Winkelgeschwindigkeiten angenommen werden. Durch die Eingabe eines Feldes von Winkelgeschwindigkeiten ω(t) oder von Drehwinkeln XWe(t) der Welle für jeden zu berechnenden Zeitpunkt JT=1 bis NT können beliebige Geschwindigkeitsprofile abgebildet werden.
Einer der wichtigsten Fälle, wo zeitlich variable Winkelgeschwindigkeiten berücksichtigt werden müssen, sind Lager mit einer pendelnden Wellendrehung. Beispielhaft dafür steht das Kolbenbolzenlager in Verbrennungsmotoren. Um für grundsätzliche Untersuchungen die Modellierung einer Pendelbewegung mit der Eingabe weniger Parameter zu realisieren, wurde im Programm SIRIUS folgende Funktion zur Darstellung von Pendelbewegungen implementiert
![]()
mit
| XWeAmp | Amplitude des Wellendrehwinkels XWe |
| XWeMit | Mittelwert des Wellendrehwinkels XWe |
| ωWe | Phasenwinkelgeschwindigkeit des Wellendrehwinkels XWe |
| ΦWe | Phasenwinkel des Wellendrehwinkels XWe zum Zeitpunkt t=0 |
Durch Differentiation der Gleichung (2.014) ergibt sich die Funktion der Winkelgeschwindigkeit ωWe(t) mit
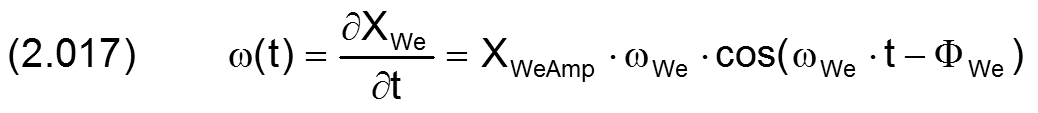
HINWEIS: Beachte den Unterschied zwischen ω(t), der zeitlich variablen Wellendrehgeschwindigkeit, und ωWe , der zeitlich konstanten Phasenwinkelgeschwindigkeit der Drehschwingung der Welle.
Im Programm SIRIUS wird das Schmiermittel als eine Newtonsche Flüssigkeit angenommen. Die dynamische Viskosität η ist dabei die wichtigste quantifizierbare Eigenschaft der Schmierflüssigkeit, von der wesentlich die Tragfähigkeit des Lagers abhängt.
Die Hersteller von Schmierstoffen geben als Stoffkennzahl üblicher Weise die kinematische Viskosität ν bei einer Temperatur von 40°C an. Dieser Wert entspricht der Angabe der Viskositätsklasse Vg nach DIN 51 519. Hinzu kommt, dass die Viskosität der üblichen Mineralöle stark von der Temperatur abhängig ist. Deshalb muss für die Berechnung eines konkreten Lagers die Betriebstemperatur bekannt sein und die kinematische Viskosität bei 40°C (= Viskositätsklasse VG) auf die dynamische Viskosität η bei Betriebstemperatur umgerechnet werden. Ist die Betriebstemperatur nicht genau bekannt oder schwankt diese bei verschiedenen Betriebsbedingungen, so muss der Nachweis der Tragfähigkeit des Lagers für verschiedene Betriebstemperaturen und dementsprechend mit verschiedenen dynamischen Viskositäten erfolgen.
Für die üblichen Mineralöle liefert nachfolgende empirische Formel [15] gute Ergebnisse
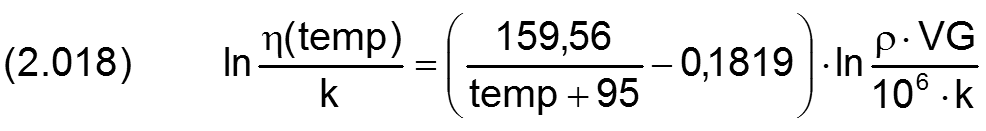
mit
| η | dynamische Viskosität in Pa·s |
| k | = 0,18 10-3 Pa·s |
| ρ | Dichte des Schmiermittels in kg/m3 |
| VG | Viskositätsklasse nach DIN 51519 (entspricht der kinematischen Viskosität ν in mm2/s) |
| temp | Temperatur in °C |
Diese Gleichung lässt sich nach η umstellen
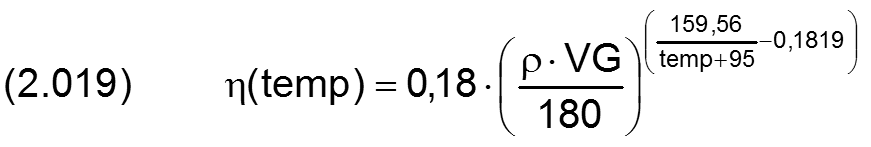
Mit oben angegebener Formel kann die dynamische Viskosität η in vielen Fällen ausreichend genau ermittelt werden. Sie ist aber nicht in das Programm SIRIUS implementiert. Diese Berechnung ist manuell auszuführen. Das Programm fragt nur die entsprechende Viskosität bei Betriebsbedingungen ab, unabhängig davon, wie diese ermittelt wurde. So können auch andere Methoden der Ermittlung der dynamischen Viskosität für andere Schmierstoffe angewendet werden. So benötigt das Programm auch keine expliziten Angaben über die Schmiermitteltemperatur und die Schmiermitteldichte.
Durch das Lagerspiel zwischen Welle und Lagerschale entsteht ein Schmierspalt h(x,z,t) der mindestens teilweise mit Schmierflüssigkeit gefüllt ist. Größe und Form dieses Schmierspalts sind eine wesentliche Voraussetzung für die Funktionsweise des Lagers. Deshalb ist eine möglichst genaue Abbildung der Spaltgeometrie eine wichtige Voraussetzung für die Auslegung eines Radialgleitlagers.
Für die Berechnung der Druckverteilung im Schmierspalt mittels der klassischen oder der erweiterten Reynoldsschen Gleichung werden Angaben über die Spalthöhe h(x,z,t) und ihre partiellen Ableitungen ∂h/∂x, ∂h/∂z und ∂h/∂t benötigt. Beginnend mit dem konzentrischen Schmierspalt h0 werden nachfolgend die verschiedenen möglichen Komponenten der resultierenden Gesamtspalthöhe h(x,z,t) gemäß ihrer Verwendung im Programm SIRIUS eingeführt.
zurück weiter zur dimensionslosen DarstellungUnter der Annahme, dass Lagerschale und Welle ideal zylindrische Oberflächen haben und die Welle konzentrisch in der Lagerschale liegt (Lagerschalenachse und Wellenachse fluchten), ergibt sich gemäß Bild 2.007 zwischen Lagerschale und Welle ein Ringspalt mit der konstanten Höhe h0
![]()
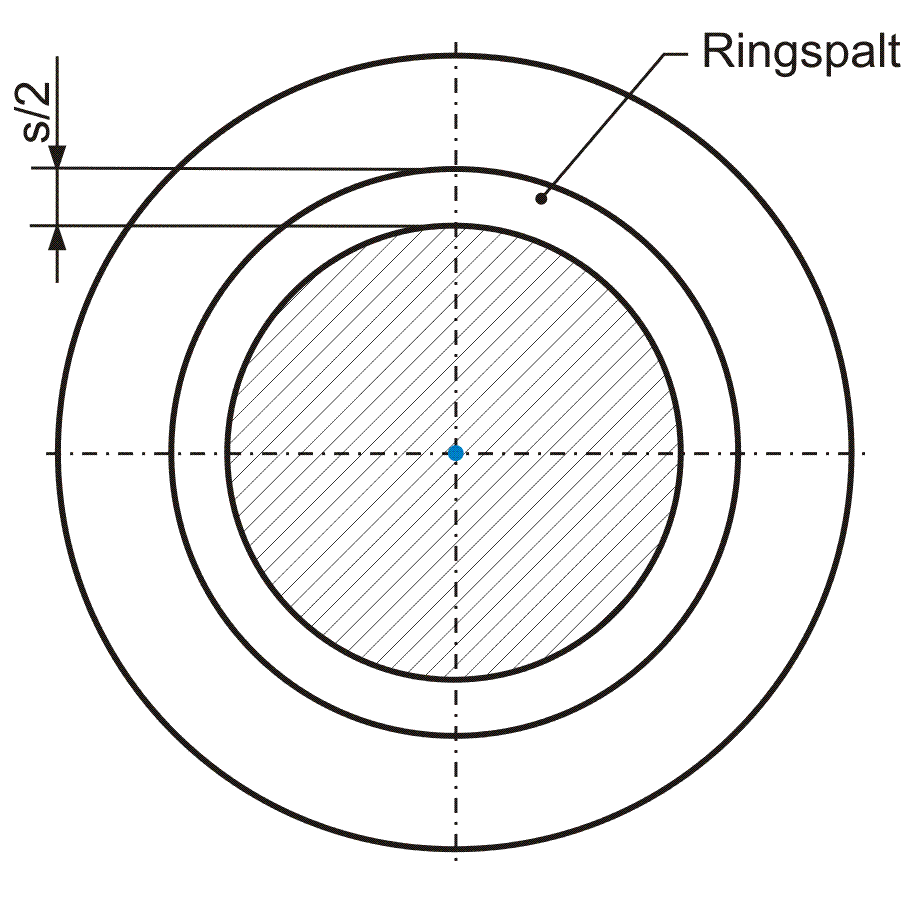
Bild 2.007: Ringspalt im ideal zylindrischen Lager mit fluchtender Wellen- und Lagerschalenachse
Wenn Lagerschale und/oder Welle nicht mehr als ideal zylindrisch angenommen werden, dann ist das (mittlere) Lagerspiel s für ein voll umschlossene Lager geben durch das Doppelte der mittleren Spalthöhe.
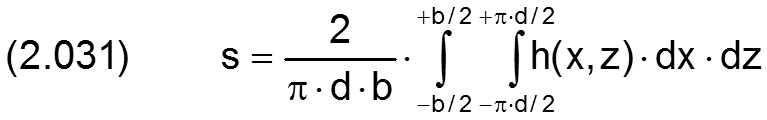
Für ein teilweise umschlossenes Lager ist ein sinnvoller analoger Wert zu wählen, indem die Integration bei einer angenommenen konzentrischen Lage von Lagerschalen- und Wellenachse erfolgt.
zurück weiter zur dimensionslosen DarstellungAufgrund mittig angreifender Lagerbelastung entsteht ein Versatz zwischen der Lagerachse und der Wellenachse. Der Betrag des Versatzes wird angegeben durch die Exzentrizität e und die Richtung der Verlagerung durch den Verlagerungswinkel XE, gemäß Bild 2.008.
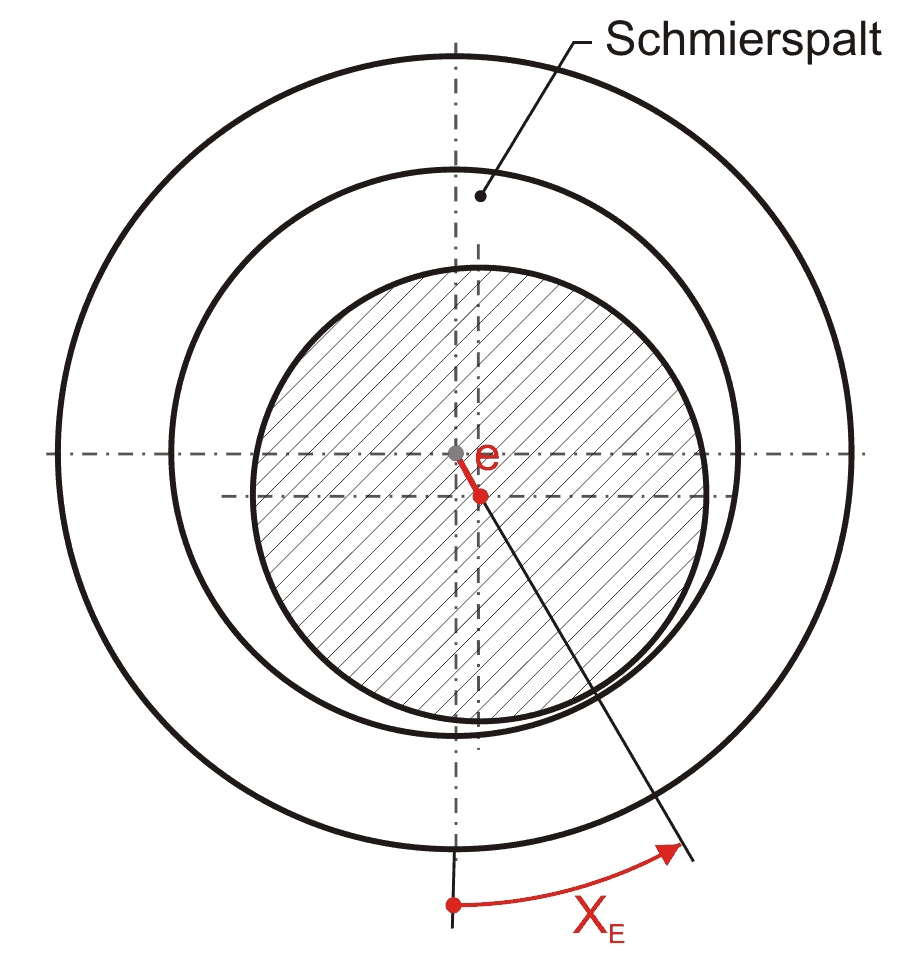
Für den einfachsten Fall eines achsparallelen Lagers mit ideal zylindrischer Welle und ideal zylindrischer Lagerschale ergibt sich eine Änderung Δh1 der Spalthöhe h gegenüber dem konstanten Ringspalt h0 in Abhängigkeit von der Exzentrizität e(t) und dem Verlagerungswinkel XE(t) durch
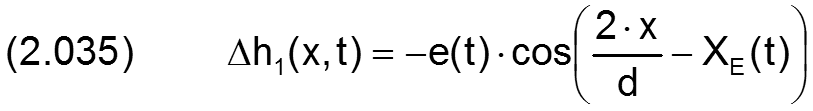
Die zugehörigen partiellen Ableitungen sind
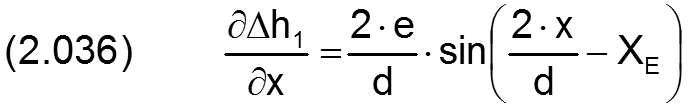
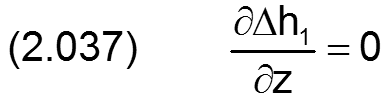
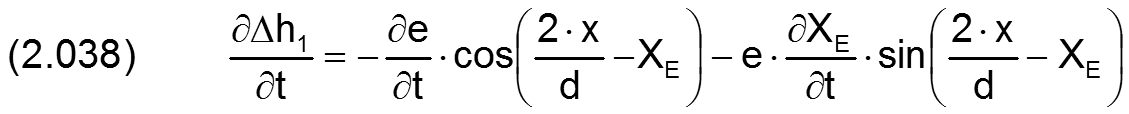
Bedingt durch das geringe Lagerspiel s im Verhältnis zum Wellendurchmesser d stellen diese Gleichungen eine ausgezeichnete Approximation der Spaltgeometrie dar.
HINWEIS: Der Parameter x ist hier die dimensionsbehaftete Koordinate x des lagerschalenfesten Koordinatensystems x-y-z gemäß Bild 2.003 und nicht die Winkelangabe x in grd wie im Programm SIRIUS verwendet. XE ist dagegen eine Winkelangabe gemessen in Radiant, die damit gleichzeitig der dimensionslosen Umfangskoordinate des Koordinatensystems X-Z im dimensionslos gemachten Lager entspricht.
Statt durch den Betrag e und den Verlagerungswinkel XE ist die Exzentrizität auch bestimmt durch ihre Komponenten e1 und e2, wobei gilt
![]()

Die Änderung der Spalthöhe h1 infolge der Exzentrizität kann auch durch die Komponenten e1 und e2 angegeben werden.
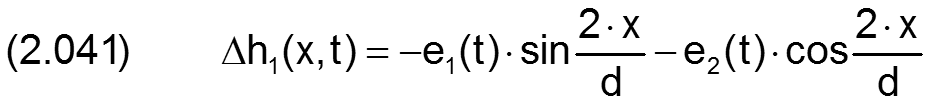
Die zugehörigen partiellen Ableitungen sind dann
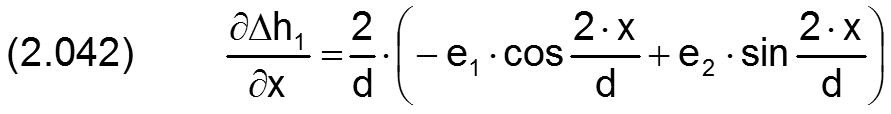
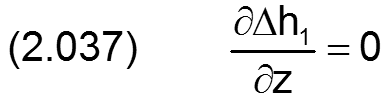
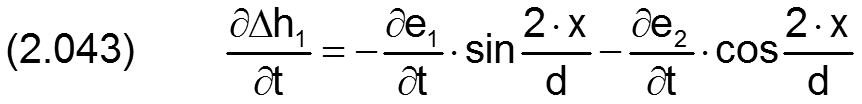
Bild 2.009 zeigt die achsparallele Verlagerung der Wellenachse (rot) gegenüber der Lagerschalenachse (blau) im Verlagerungsraum (grün) bei ideal zylindrischer Welle und Lagerschale.
 |
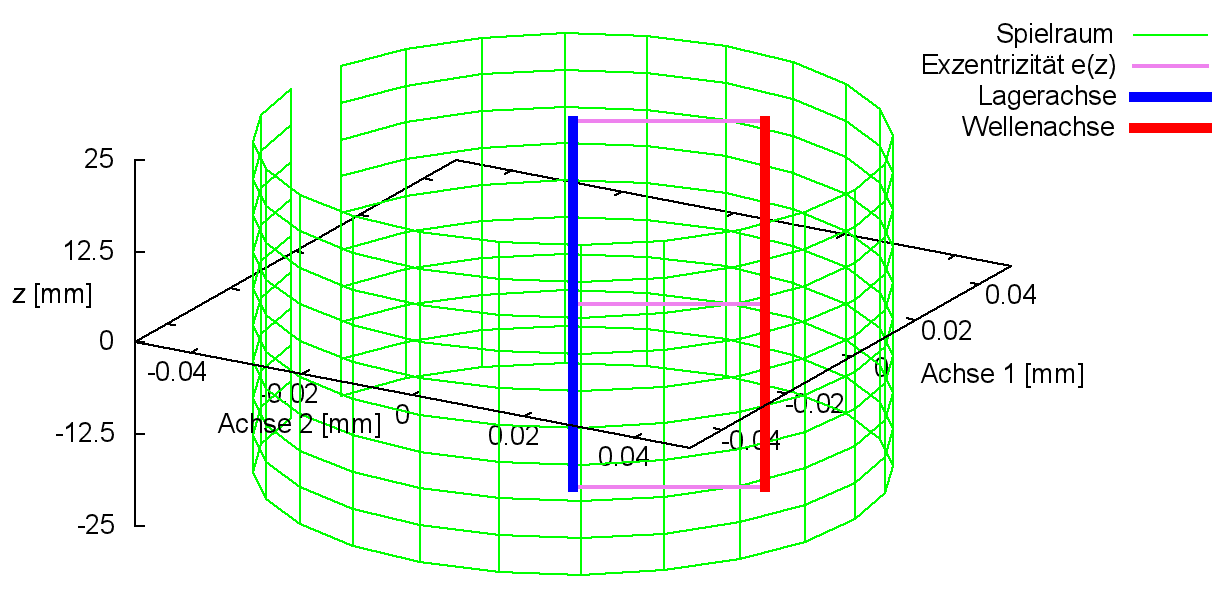 |
Aus dem Spielraum ist zu entnehmen, dass die maximale Exzentrizität kleiner sein muss als das halbe Lagerspiel.
![]()
Das gilt aber nur für das ideal zylindrische achsparallele Lager.
Die Verlagerung der Welle innerhalb der Lagerschale gegeben durch die Parameter der Exzentrizität e und den Verlagerungswinkel XE bzw. durch die Komponenten der Exzentrizität e1 und e2 können als konstant oder als zeitlich variabel angenommen werden. Wenn die Verlagerungsbahn aus einer vorgegebenen Lagerbelastung berechnet wird, werden die Parameter der Exzentrizität e(t) und XE(t) bzw. e1(t) und e2(t) punktweise für NT Zeitpunkte berechnet. Wenn die Lagerbelastung über die Zeit aus einer vorgegebenen (gemessenen) Verlagerungsbahn berechnet werden soll, dann können die entsprechenden Parameter der Exzentrizität für die zur berechnenden NT Zeitpunkte punktweise eingegeben werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lager, wenn noch keine konkreten Daten für die Verlagerungsbahn bekannt sind, können komplette Verlagerungsbahnen auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung von Verlagerungsbahnen implementiert.
![]()
![]()
mit
| e1Amp | Amplitude der Exzentrizität e1 |
| e1Mit | Mittelwert der Exzentrizität e1 |
| ω1 | Phasenwinkelgeschwindigkeit der Exzentrizität e1 |
| Φ1 | Phasenwinkel der Exzentrizität e1 zum Zeitpunkt t=0 |
| e2Amp | Amplitude der Exzentrizität e2 |
| e2Mit | Mittelwert der Exzentrizität e2 |
| ω2 | Phasenwinkelgeschwindigkeit der Exzentrizität e2 |
| Φ2 | Phasenwinkel der Exzentrizität e2 zum Zeitpunkt t=0 |
Bild 2.010 zeigt ein Beispiel für eine Verlagerungsbahn mit den Werten e1Amp = 0,01mm; e1Mit = 0 mm; ω1 = 3000 grd/s; Φ1 = 90 grd; e2Amp = 0,025 mm; e2Mit = 0,015 mm; ω2 = 3000 grd/s; Φ2 = 0 in einem Lagerspielraum von s=0,1 mm und b=50 mm.
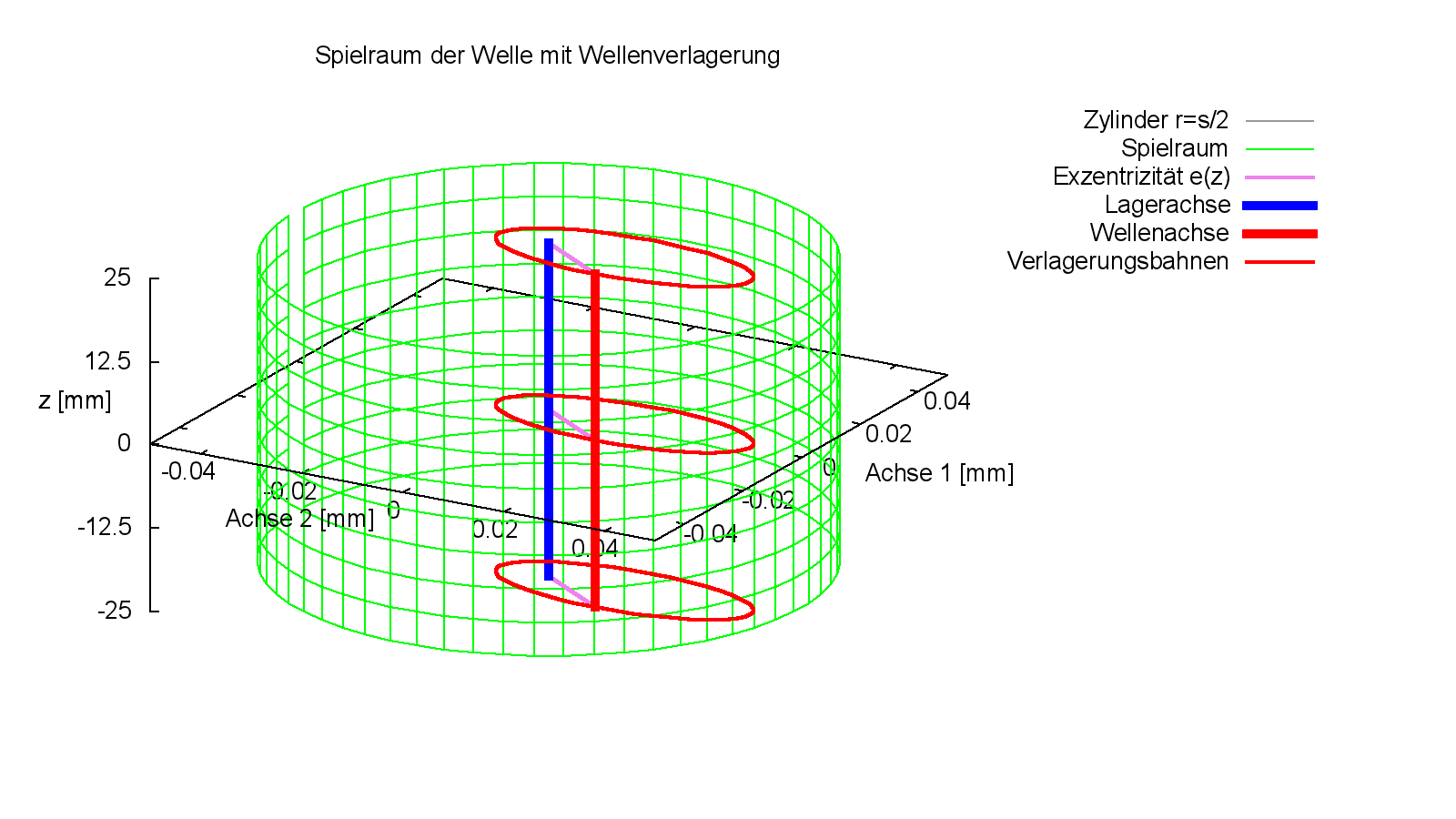
Bild 2.010: Beispiel für eine Verlagerungsbahn, die durch die Parameter einer Funktion vorgegeben wurde (Animation)
Für die Berechnung der partiellen Ableitung ∂h1/∂t der Spalthöhe über die Zeit werden auch die Ableitungen der Exzentrizitäten über die Zeit benötigt. Sie können exakt berechnet werden gemäß den Gleichungen (2.047) und (2.048) und brauchen deshalb hier nicht näherungsweise ermittelt werden wie für den Fall, wenn die Exzentrizitäten punktweise über die Zeit eingegeben werden.
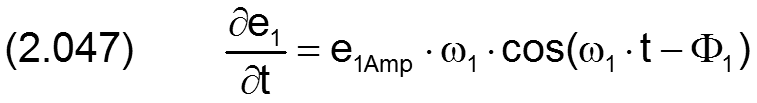
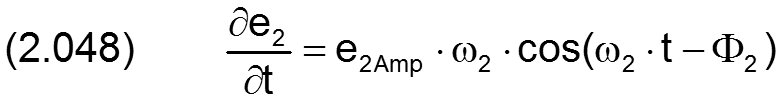
Aufgrund von Fertigungstoleranzen und Verformungen der benachbarten Maschinenelemente eines Lagers im Betrieb entstehen Fluchtungsfehler zwischen Welle und Lagerschale. Man spricht dann von einer Verkantung der Welle im Lager. Diese Verkantung kann im Programm SIRIUS berücksichtigt werden. Die Verkantung wird hier in Bezug auf das Lager als ein externer Parameter behandelt, der vorzugeben ist und nicht durch den Schmierfilmdruck beeinflusst wird. Die Verkantung kann zeitlich variabel vorgegeben werden.
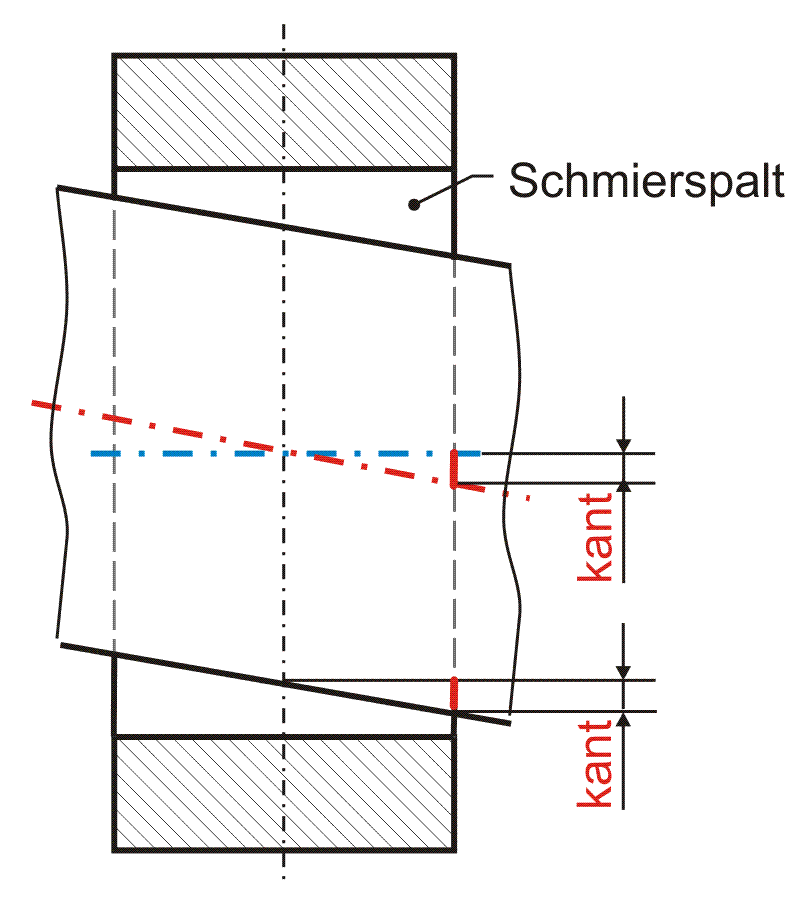
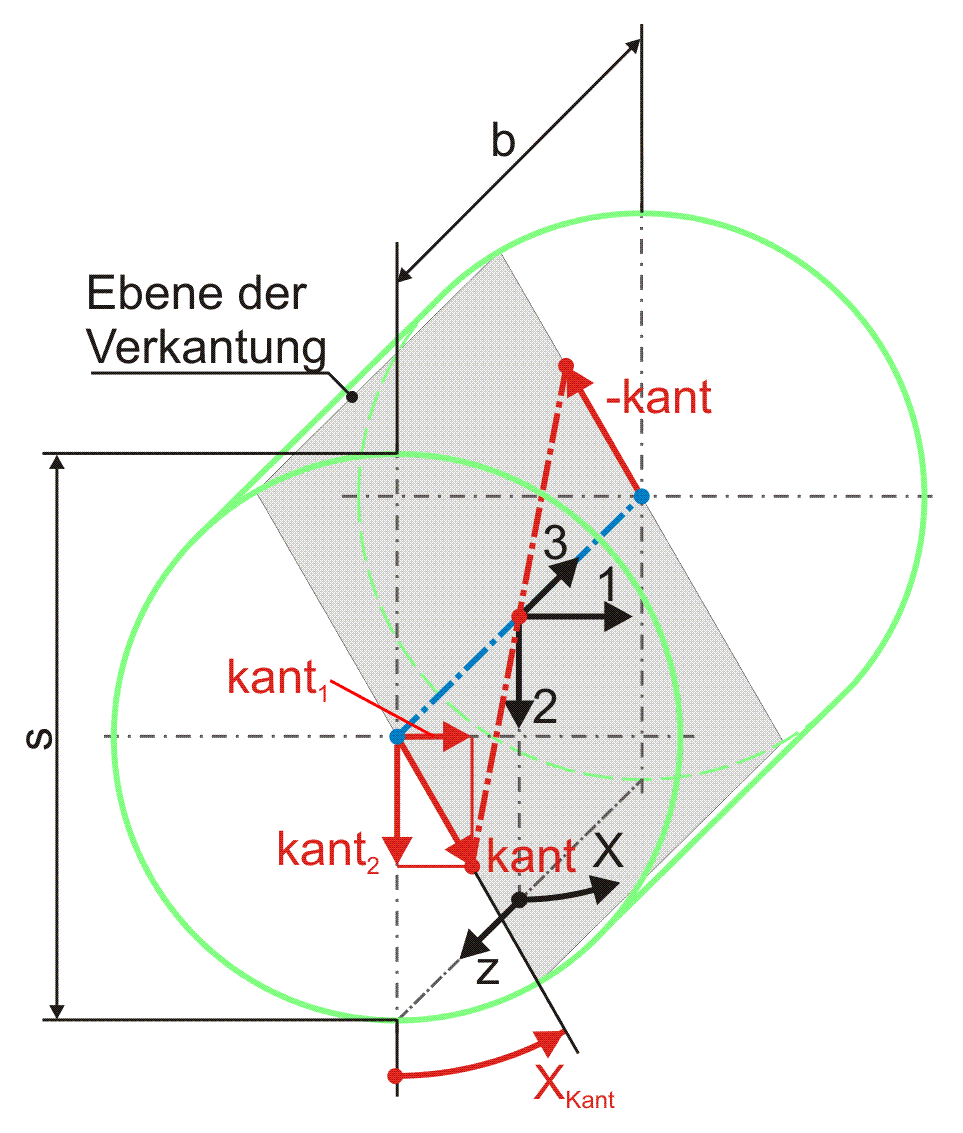
Reine Verkantung (ohne zusätzliche Exzentrizität der Welle) wird gemäß Bild 2.011 bestimmt durch den Betrag der Verkantung kant. Er ist gegeben durch den Versatz der Wellenachse an den Lagerrändern bezogen auf die Achse der Lagerschale, während die Wellenachse in der Mitte des Lagers die Lagerschalenachse schneidet. Die Verkantung kann in einer beliebigen Verkantungsebene erfolgen. Bei der reinen Verkantung ist diese gegeben durch die Ebene, in der sowohl die Lagerschalenachse als auch die Wellenachse liegt (gemäß Bild 2.012). Ihre Lage wird angegeben durch den Verkantungswinkel XKant. Das ist der Winkel zwischen der Ebene 2-3 des Koordinatensystems 1-2-3 und der Verkantungsebene gemessen in Richtung der positiven X-Achse.
 |
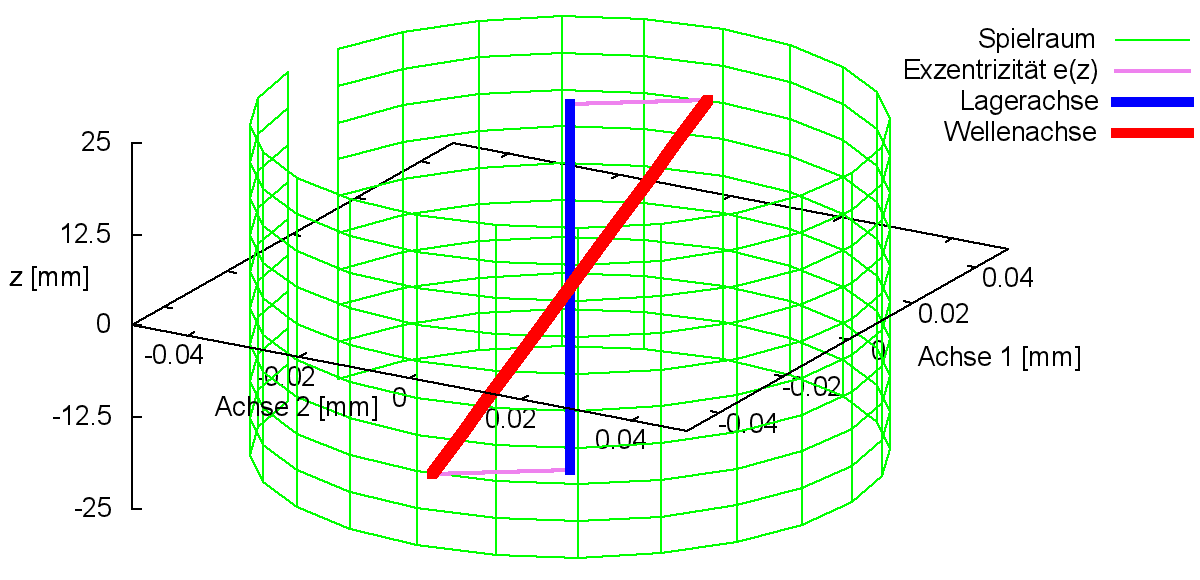 |
Im Spielraum des ideal zylindrischen Lagers ist zu erkennen, dass der Betrag der Verkantung aus kinematischen Gründen kleiner sein muss als das halbe Spiel s.
![]()
Bei einem positiven Wert für kant zeigt der Vektor der Verkantung am axialen Lagerende z=zEnd=+b/2 in Richtung des Schenkels des Winkels XKant gemäß Bild 2.012.
HINWEIS: Aus funktioneller Sicht sollte die Verkantung wesentlich kleiner sein als das halbe Lagerspiel, weil eine zu große Verkantung die Ausbildung einer ausreichenden Exzentrizität verhindern kann, die für eine notwendige hydrodynamische Tragfähigkeit des Lagers erforderlich ist. Das gilt übrigens auch für alle weiteren nachfolgend beschriebenen Formabweichungen von der ideal zylindrischen Form der Lagerbauteile.
Die Änderung Δh2 der Schmierspalthöhe h durch Verkantung lässt sich durch folgende Funktion beschreiben.
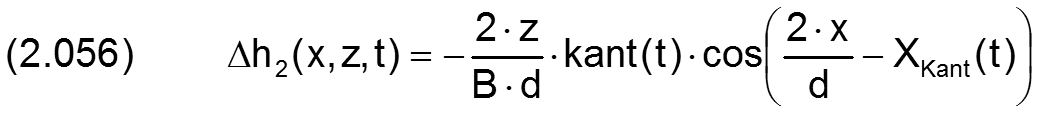
Die zugehörigen partiellen Ableitungen sind gegeben durch

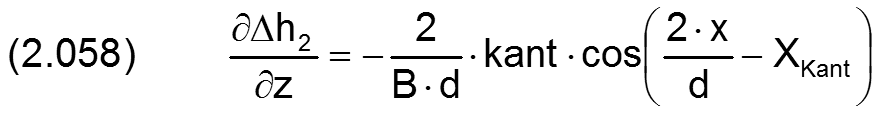
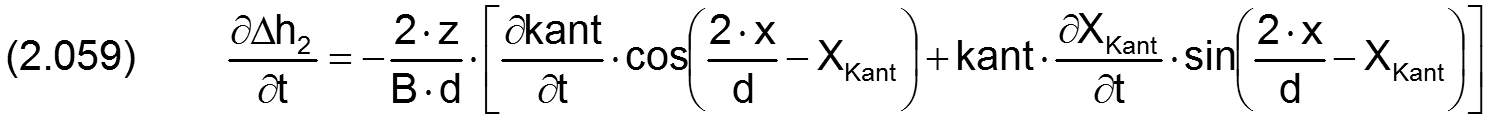
HINWEIS: Der Parameter x ist hier die dimensionsbehaftete Koordinate x des lagerschalenfesten Koordinatensystems x-y-z gemäß Bild 2.003 und nicht die Winkelangabe x in grd wie im Programm SIRIUS verwendet. XKant ist dagegen eine Winkelangabe gemessen in Radiant, die damit gleichzeitig der dimensionslosen Umfangskoordinate des Koordinatensystems X-Z im dimensionslos gemachten Lager entspricht.
Statt durch den Betrag kant und den Winkel XKant der Verkantungsebene ist die Verkantung auch bestimmt durch ihre Komponenten kant1 und kant2, wobei gilt
![]()

Die Änderung der Spalthöhe Δh2 infolge der Verkantung kann auch durch die Komponenten kant1 und kant2 angegeben werden.
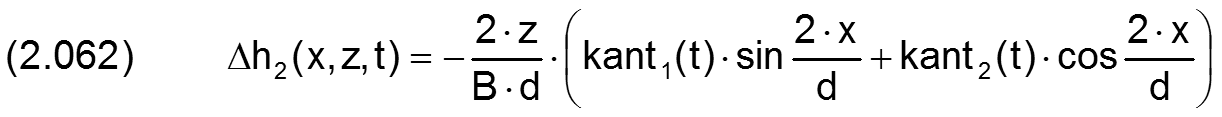
Die zugehörigen partiellen Ableitungen sind dann
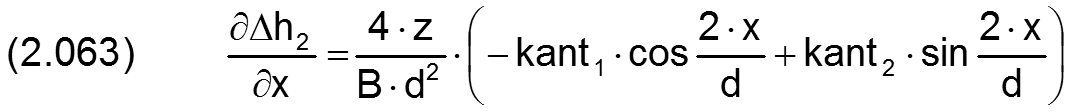
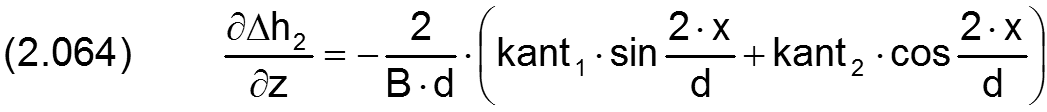
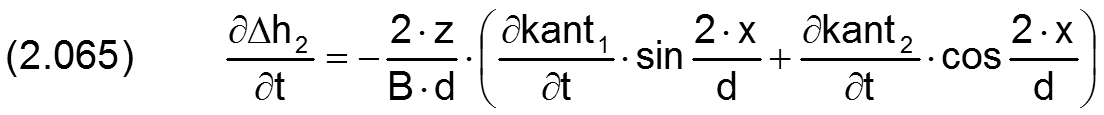
Eine mit beliebiger Lage innerhalb des Spielraums angeordnete (verkantete) Welle lässt sich jetzt darstellen durch die Überlagerung einer achsparallelen Exzentrizität gegeben durch die Parameter e und XE und eine reine Verkantung gegeben durch die Parameter kant und XKant gemäß Bild 2.013. In der Prinzipskizze (links) ist außerdem die minimale Spalthöhe hMin (rot) eingetragen, deren Größe und Lage im Spielraum leicht zu erkennen ist. Da eine gewisse Verkantung in der Praxis kaum zu vermeiden ist, liegt die minimale Spalthöhe in der Regel an einem der Lagerränder
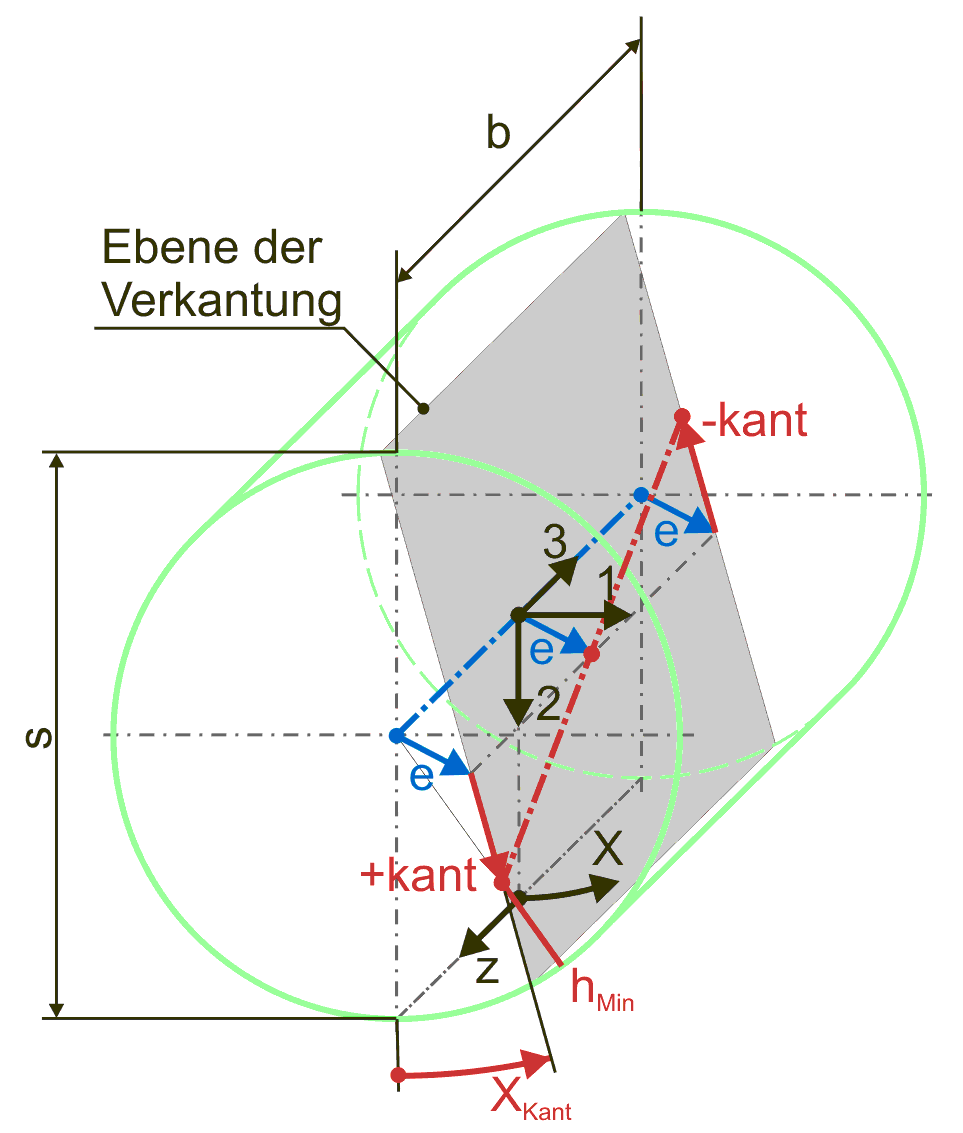 |
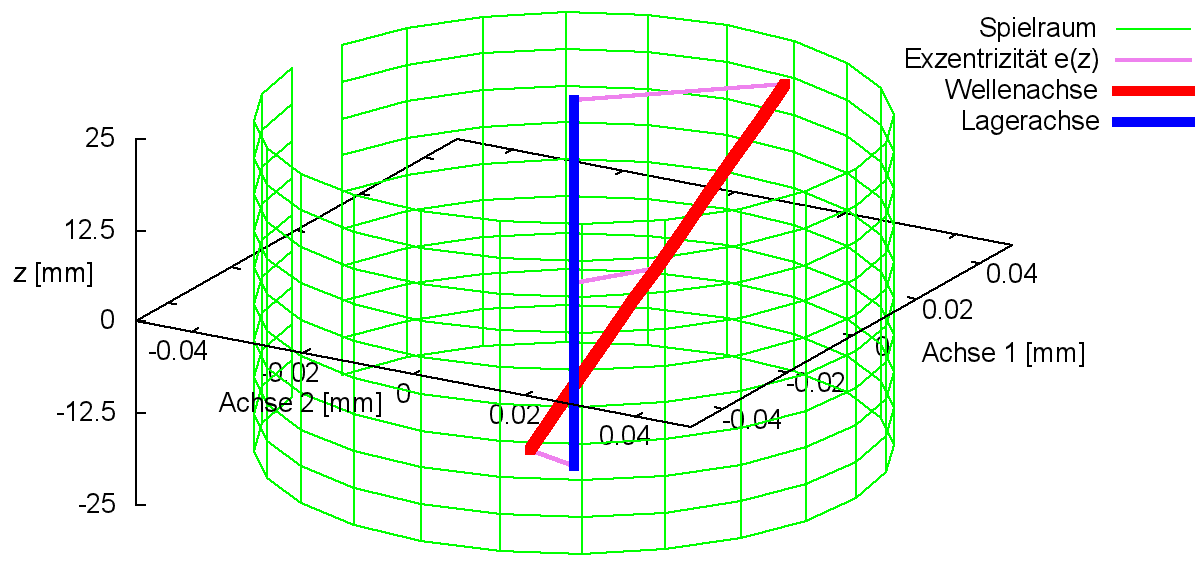 |
Die Verkantung der Welle innerhalb der Lagerschale, gegeben durch den Betrag kant und den Winkel XKant der Verkantungsebene bzw. durch die Komponenten kant1 und kant2 , können konstant sein oder als zeitlich variabel angenommen werden. Die Werte für die zeitabhängigen Werte der Verkantung können für alle NT Zeitpunkte der Berechnung punktweise eingegeben oder eingelesen werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lager, wenn noch keine konkreten Daten für die Verkantung bekannt sind, können komplette Verläufe der Verkantung auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung der Wellenverkantung implementiert.
![]()
![]()
mit
| kant1Amp | Amplitude der Komponente kant1 der Wellenverkantung |
| kant1Mit | Mittelwert der Komponente kant1 der Wellenverkantung |
| ω1Kant | Phasenwinkelgeschwindigkeit der Komponente kant1 der Verkantung |
| Φ1Kant | Phasenwinkel der Komponente kant1 der Verkantung zum Zeitpunkt t=0 |
| kant2Amp | Amplitude der Komponente kant2 der Wellenverkantung |
| kant2Mit | Mittelwert der Komponente kant2 der Wellenverkantung |
| ω2Kant | Phasenwinkelgeschwindigkeit der Komponente kant2 der Verkantung |
| Φ2Kant | Phasenwinkel der Komponente kant2 der Verkantung zum Zeitpunkt t=0 |
Bild 2.014 zeigt ein Beispiel für einen Verlauf der Verkantung mit den Werten kant1Amp = 0,0125mm; kant1Mit = 0 mm; ω1Kant = 6000 grd/s; Φ1Kant = 0 grd; kant2Amp = 0,025 mm; kant2Mit = 0; ω2Kant = 3000 grd/s; ΦKant2 = 0 in einem Lagerspielraum von s=0,1mm und b=50 mm.
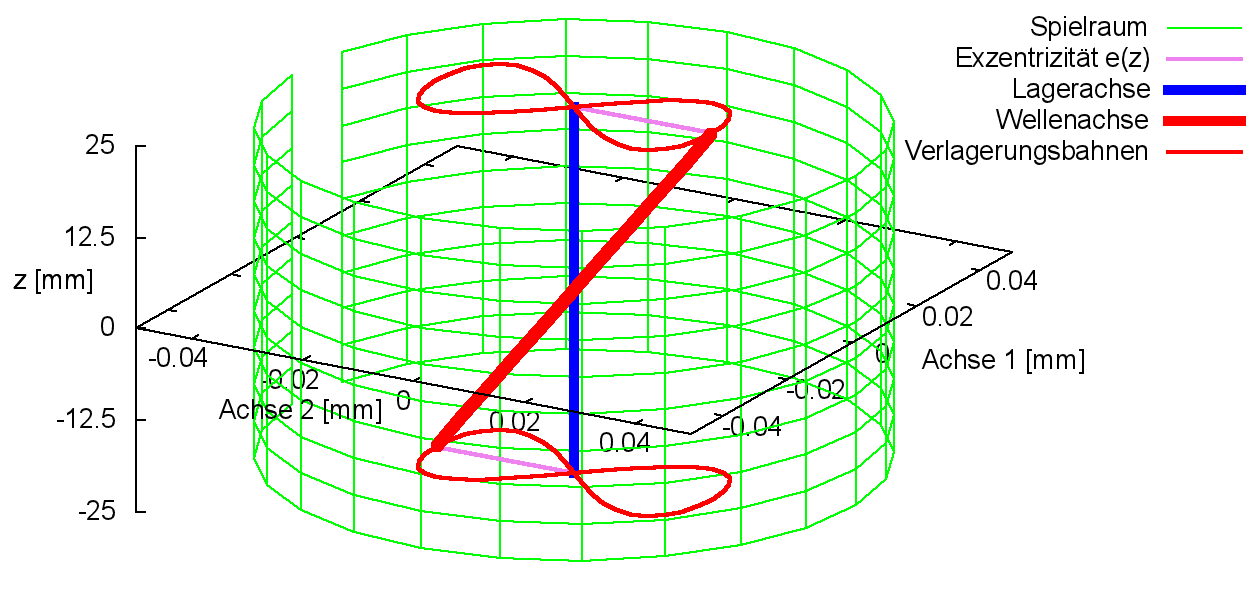
Bild 2.014: Beispiel für einen Verlauf der Verkantung, der durch die Parameter einer Funktion vorgegeben wurde (Animation)
Für die Berechnung der partiellen Ableitung ∂h2/∂t der Spalthöhe über die Zeit wird auch die Ableitung der Verkantung über die Zeit benötigt. Sie können exakt berechnet werden gemäß den Gleichungen (2.068) und (2.069) und brauchen deshalb hier nicht näherungsweise ermittelt werden wie für den Fall, wenn die Verkantung punktweise über die Zeit eingegeben werden.


Das relative Lagerspiel S=s/d von Gleitlagern liegt im Bereich von ca. 1‰. Wegen der geringen Abmessungen der daraus resultierenden Schmierspalthöhe h müssen in der Lagerdimensionierung oft auch kleinste Formabweichungen von Welle und Lagerschale berücksichtigt werden. Diese können durch Formabweichungen in der Fertigung, durch Verformungen und Abrieb im Betrieb entstehen. Beliebige gemessene oder extern berechnete Formabweichungen der Lagerschale ΔhLa(x,z) und/oder der Welle ΔhWe0(x,z) können als Felder für jeden Gitterpunkt der abgewickelten Schmierspaltfläche in das Programm SIRIUS eingelesen werden.
HINWEIS: Bei punktweise gegebenen Formabweichungen von Welle und Lagerschale ist anzustreben, dass die idealen Zylinder, die als Basis für die Angabe der jeweiligen Formabweichungen angenommen werden, dem mittleren Durchmesser des jeweiligen Bauteils entspricht, weil dann die Differenz dieser beiden mittleren Durchmesser dem mittleren Lagerspiel entspricht. Diese Forderung ist für die punktweise gegebenen Formabweichungen im Programm SIRIUS nicht zwingend.
Das Feld ΔhWe0(NZ,NX) beschreibt die punktweise angegebene Formabweichung der Wellengleitfläche bezogen auf eine angenommene ideale Zylinderfläche, deren (mittlerer) Durchmesser zur Bestimmung des mittleren Lagerspiels s herangezogen wird. Per Definition vergrößern positive Werte für hWe0 die örtliche Spalthöhe. Außerdem sind die Werte dieses Feldes bezogen auf ein Gitternetz, welches mit der Wellenoberfläche fest verbunden ist und durch die Wellendrehung mitbewegt wird. Damit ergibt sich die Formabweichung ΔhWe(x,z,t) der Welle bezogen auf das lagerschalenfeste Koordinatensystem x-y-z durch die Beziehung
![]()
Dabei ist xWe(t) die Umfangskoordinate der Wellendrehung bzw. XWe(t) der Drehwinkel der Welle zum Zeitpunkt t und xAnf0 der Versatz zwischen dem wellenfesten und dem Lagerschalenfesten Gitternetz, wenn der Drehwinkel der Welle xWe(t)=0 ist gemäß Bild 4.010.

Bild 4.010: Versatz der Gitternetze von Welle und Lagerschale
Die partiellen Ableitungen ∂hWe/∂x und ∂hWe/∂z werden programmintern durch numerische Differentiation ebenfalls punktweise ermittelt. Die Formabweichung hWe der Wellenoberfläche ist zeitlich konstant bezogen auf die Welle. Bezogen auf das lagerschalenfeste Koordinatensystem x-y-z ist sie zeitlich variabel. Deshalb gilt für die partielle Ableitung über die Zeit bezogen auf das lagerschalenfeste Koordinatensystem x-y-z
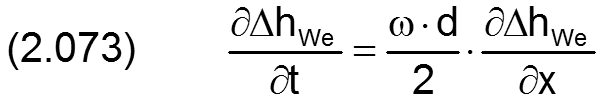
Das Feld ΔhLLa(NZ,NX) beschreibt die punktweise angegebene Formabweichung der Lagerschalengleitfläche bezogen auf eine angenommene ideale Zylinderfläche, deren (mittlerer) Durchmesser zur Bestimmung des mittleren Lagerspiels s herangezogen wird. Per Definition vergrößern positive Werte für ΔhLa die örtliche Spalthöhe. Die partiellen Ableitungen ∂hLa/∂x und ∂hLa/∂z der Formabweichungen der Lagerschale werden programmintern durch numerische Differentiation ebenfalls punktweise ermittelt. Die Formabweichung ΔhLa der Lagerschale ist zeitlich konstant, deshalb gilt bezogen auf das Lagerschalenfeste Koordinatensystem x-y-z
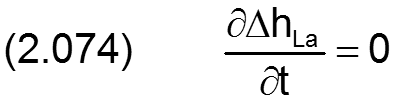
HINWEIS: Mit dem Feld ΔhLa(NZ,NX) können auch extern berechnete zeitlich konstante elastische Formabweichungen der Lagerschale berücksichtigt werden. Elastische Formabweichungen die programmintern über eine Elastizitätsmatrix chp berechnet werden sollen und so auch instationäre Verformungen erfassen können, werden nicht durch ΔhLa(NZ,NX) erfasst. Siehe dazu Abschnitt 2.1.2.17.
Da die Ermittlung und Eingabe punktweise gegebener Formabweichungen recht aufwendig ist, sind für prinzipielle Untersuchungen des Einflusses von Formabweichungen im Programm SIRIUS einige durch Funktionen modelliert, so dass ihre Eingabe einfach durch wenige Parameter realisiert werden kann. Nachfolgend sind die verfügbaren Formabweichungen und die zugehörigen Funktionen angegeben.
zurück weiter zur dimensionslosen Darstellung
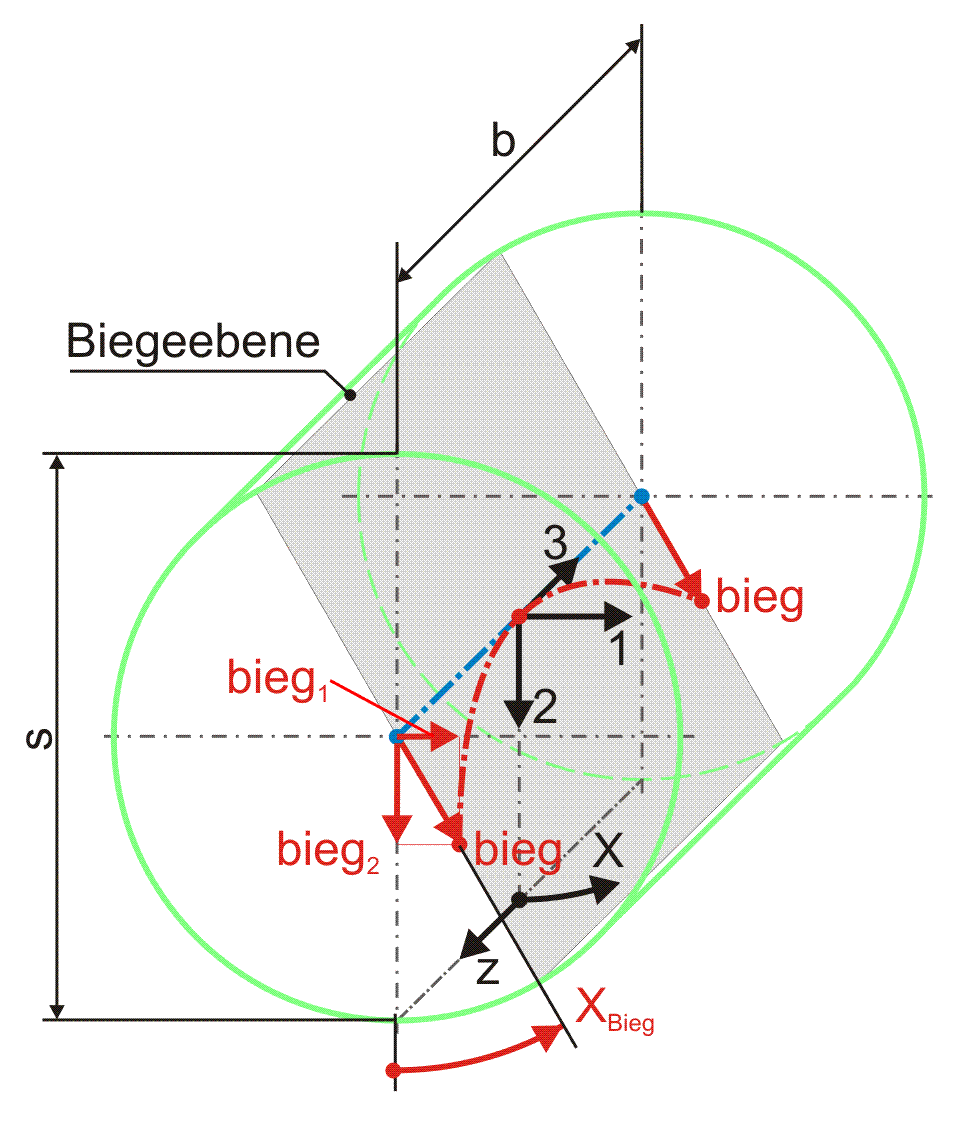
Reine Wellenbiegung (ohne zusätzliche Exzentrizität oder Verkantung der Welle) wird gemäß Bild 2.015 bestimmt durch den Betrag der Biegung bieg. Er ist gegeben durch die lokale Exzentrizität der Wellenachse an den Lagerrändern bezogen auf die Achse der Lagerschale, während die Wellenachse in der Mitte des Lagers die Lagerschalenachse tangiert. Die reine Wellenbiegung kann in einer beliebigen Ebene liegen, die die Achse der Lagerschale schneidet (Bild 2.016 links). Die Lage dieser Ebene wird durch den Winkel XBieg angegeben. Das ist der Winkel zwischen der Ebene 2-3 des Koordinatensystems 1-2-3 und der Biegeebene gemessen in Richtung der positiven X-Achse.
 |
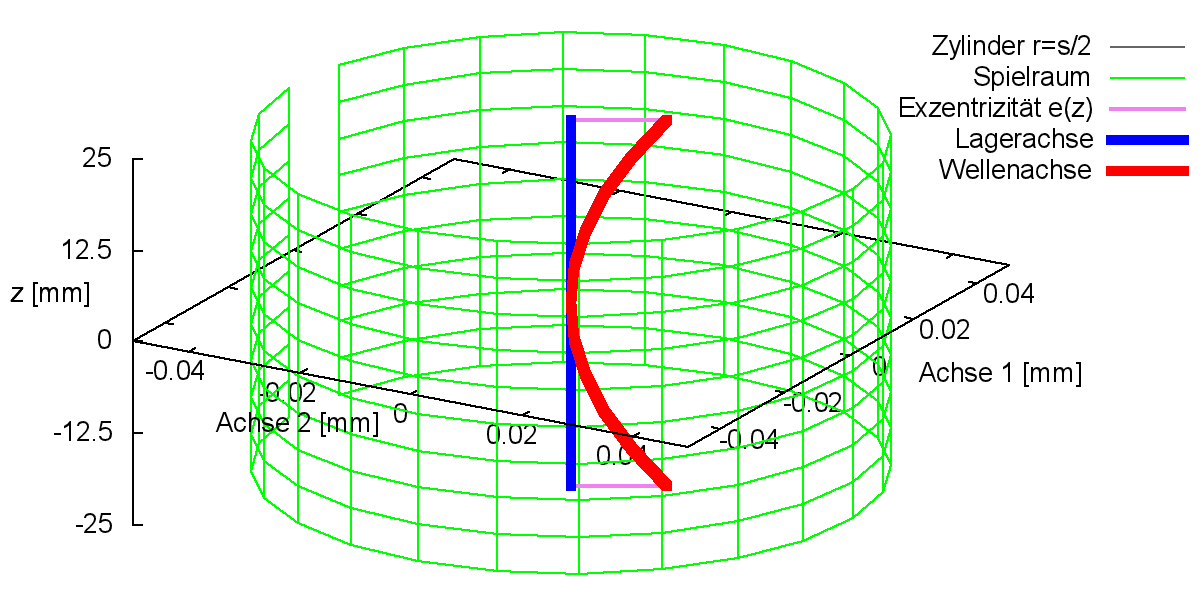 |
Bei reiner Biegung muss diese kleiner sein als das halbe Lagerspiel. Bei Überlagerung mit einer entgegen gerichteten achsparallelen Verlagerung könnte die Biegung theoretisch aber auch einen Wert annehmen bis knapp an das Lagerspiel s, was aber unrealistisch ist, weil dann kaum noch eine hydrodynamische Tragfähigkeit des Lagers gegeben ist.
![]()
Bei einem positiven Wert für bieg zeigt der Vektor der Biegung in Richtung des Schenkels des Winkels XBieg gemäß Bild 2.016. Die Änderung Δh3 der Schmierspalthöhe h durch reine Wellenbiegung lässt sich näherungsweise durch folgende Funktion beschreiben.
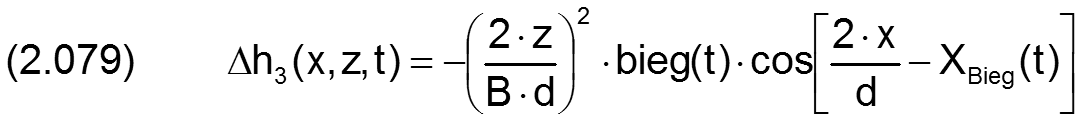
Wegen der geringen Spalthöhe h gegenüber der Lagerbreite b stellt die quadratische Funktion eine ausgezeichnete Approximation für eine Wellenbiegung mit konstantem Biegeradius über die Lagerbreite dar.
Die zugehörigen partiellen Ableitungen sind dann gegeben durch
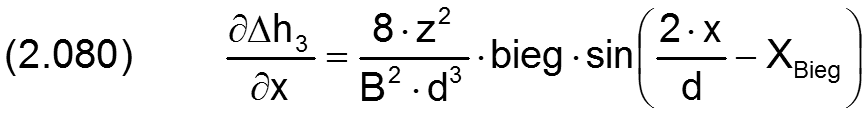

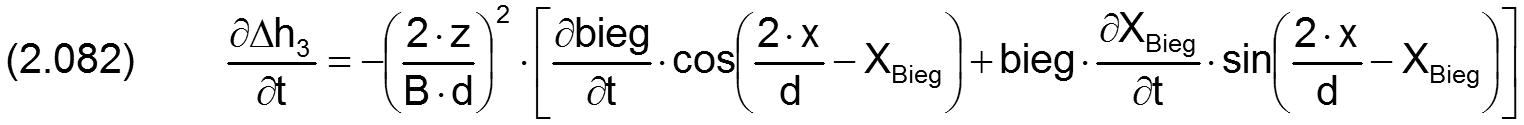
HINWEIS: Der Parameter x ist hier die dimensionsbehaftete Koordinate x des lagerschalenfesten Koordinatensystems x-y-z gemäß Bild 2.003 und nicht die Winkelangabe x in grd wie im Programm SIRIUS verwendet. XBieg ist dagegen eine Winkelangabe gemessen in Radiant, die damit gleichzeitig der dimensionslosen Umfangskoordinate des Koordinatensystems X-Z im dimensionslos gemachten Lager entspricht.
Statt durch den Betrag bieg und den Winkel XBieg der Biegeebene ist die Biegung auch bestimmt durch ihre Komponenten bieg1 und bieg2, wobei gilt
![]()
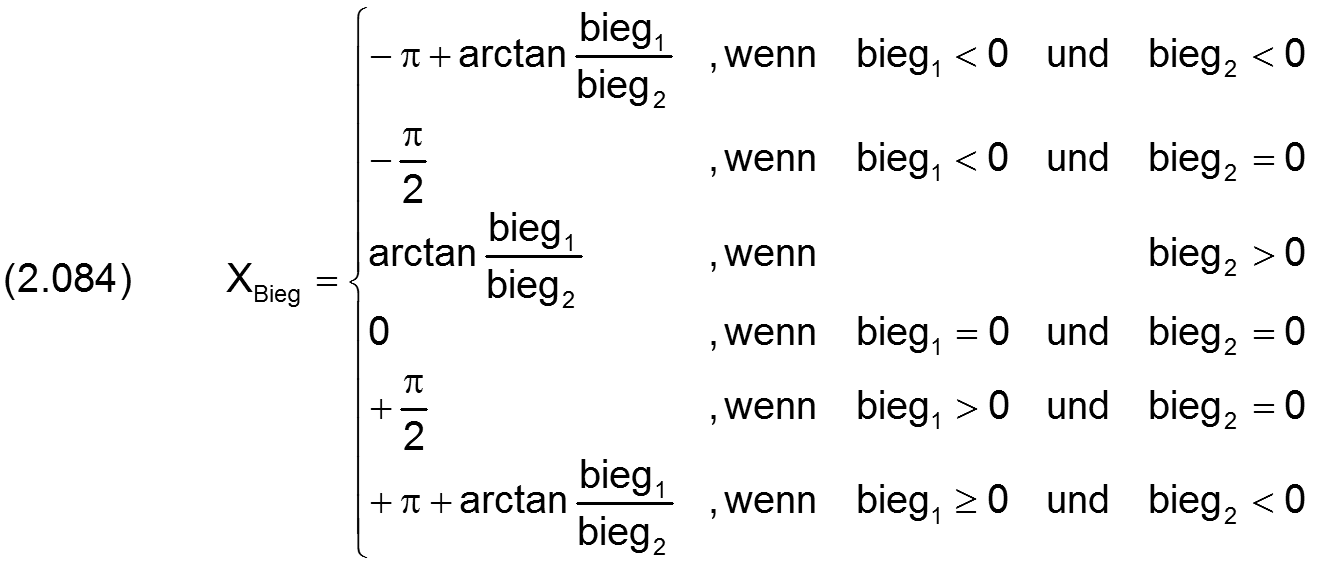
Die Änderung der Spalthöhe Δh3 infolge der Biegung kann auch durch die Komponenten bieg1 und bieg2 angegeben werden.
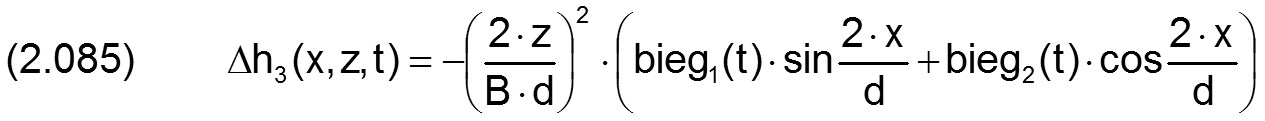
Die zugehörigen partiellen Ableitungen sind dann
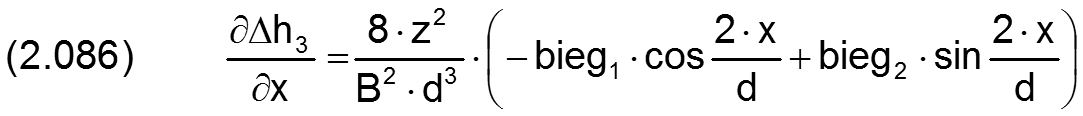
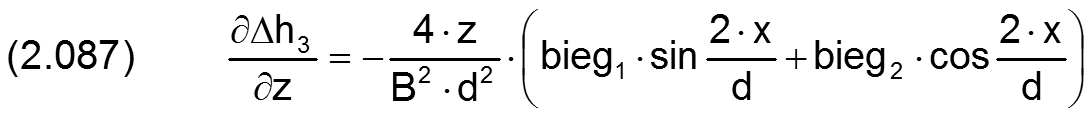
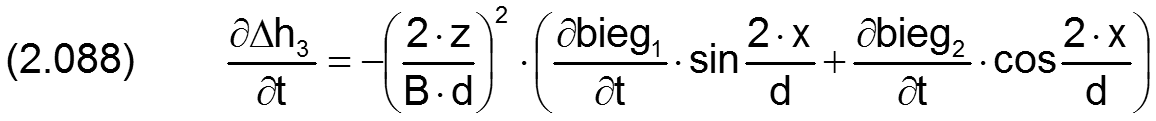
Die Wellenbiegung kann natürlich auch mit einer Exzentrizität und einer Verkantung und allen noch folgenden Formabweichungen überlagert werden.
Die Biegung der Welle innerhalb der Lagerschale gegeben durch den Betrag bieg und den Winkel XBieg der Biegeebene bzw. durch die Komponenten bieg1 und bieg2 können konstant sein oder als zeitlich variabel angenommen werden. Die Werte für die zeitabhängigen Werte der Biegung können für alle NT Zeitpunkte der Berechnung punktweise eingegeben oder eingelesen werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lager, wenn noch keine konkreten Daten für die Biegung bekannt sind, können komplette Verläufe der Biegung auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung von Wellenbiegung implementiert.
![]() <
<
![]()
mit
| bieg1Amp | Amplitude der Komponente bieg1 der Wellenbiegung |
| bieg1Mit | Mittelwert der Komponente bieg1 der Wellenbiegung |
| ω1Bieg | Phasenwinkelgeschwindigkeit der Komponente bieg1 der Biegung |
| Φ1Bieg | Phasenwinkel der Komponente bieg1 der Biegung zum Zeitpunkt t=0 |
| bieg2Amp | Amplitude der Komponente bieg2 der Wellenbiegung |
| bieg2Mit | Mittelwert der Komponente bieg2 der Wellenbiegung |
| ω2Bieg | Phasenwinkelgeschwindigkeit der Komponente bieg2 der Biegung |
| Φ2Bieg | Phasenwinkel der Komponente bieg2 der Biegung zum Zeitpunkt t=0 |
Bild 2.017 zeigt ein Beispiel für einen Verlauf der Biegung mit den Werten bieg1Amp = 0,025mm; bieg1Mit = 0 mm; ω1Bieg = 3000 grd/s; Φ1Bieg = 0; bieg2Amp = 0,025 mm; bieg2Mit = 0; ω2Bieg = 3000 grd/s; Φ2Bieg = -π/2 in einem Lagerspielraum von s=0,1mm und b=50 mm.
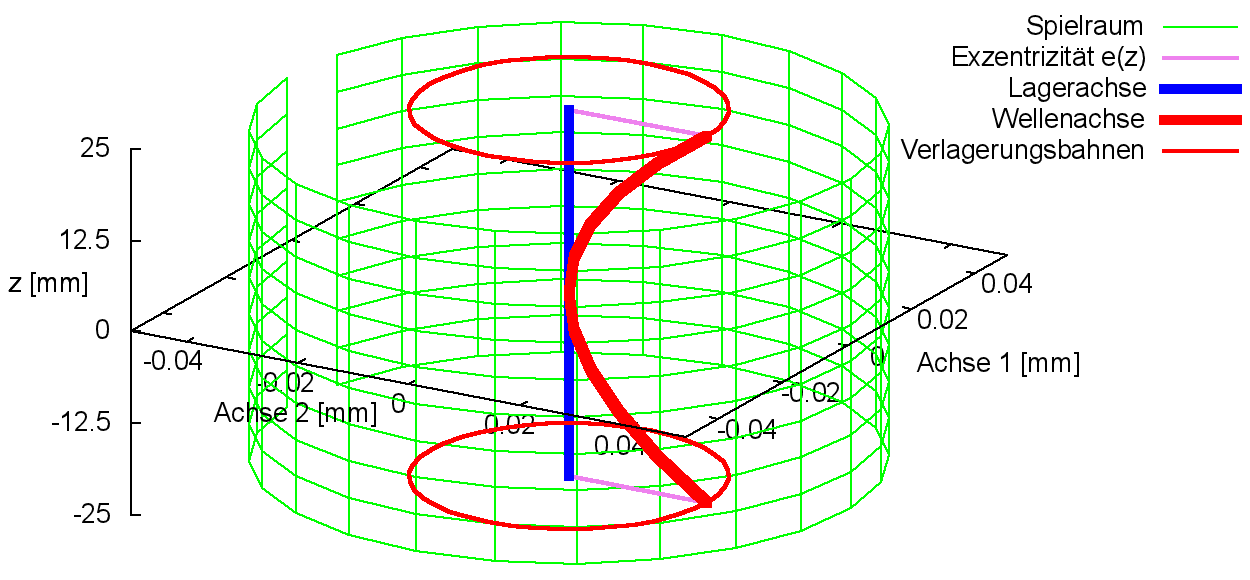
Bild 2.017: Beispiel für einen Verlauf der Biegung, der durch die Parameter einer Funktion vorgegeben wurde (Animation)
Für die Berechnung der partiellen Ableitung ∂h3/∂t der Spalthöhe über die Zeit werden auch die Ableitungen der Wellenbiegung über die Zeit benötigt. Sie können exakt berechnet werden gemäß den Gleichungen (2.091) und (2.092) und brauchen deshalb hier nicht näherungsweise ermittelt werden wie für den Fall, wenn die Biegung punktweise über die Zeit eingegeben wird.
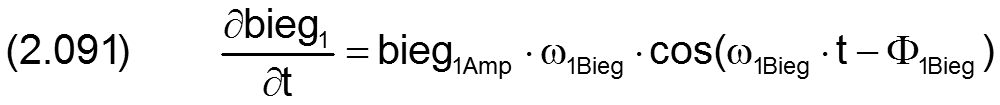
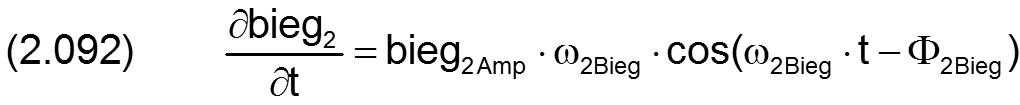
Die Lagerschale kann durch Fertigungsfehler leicht elliptische, "dreieckige", "viereckige" und andere "polygone" Formen aufweisen bis hin zu einer welligen Oberfläche. Derartige Formabweichungen über den Umfang werden in SIRIUS als zeitlich konstant und lagerschalenfest angenommen. Bild 2.018 zeigt als Beispiel ein Lager mit elliptischer Lagerschale. Zur Beschreibung dieser Unrundheit sind die drei Parameter unLa, XLa und NLa erforderlich. Die Unrundheit unLa gibt das Maximum der Abweichung an, gemessen von einer angenommenen mittleren ideal zylindrischen Form der Lagerschale. Die Stelle einer maximalen Abweichung XLa gibt den Winkel zwischen dem Ursprung des Koordinatensystems X-z und einem Maximum des Betrags der Formabweichung an, gemessen in Richtung der positiven X-Achse. Verkleinert das Maximum an der Stelle XLa die Spalthöhe, wird unLa als positiver Wert angegeben, vergrößert das Maximum die Spalthöhe als negativer Wert.
![]()
NLa ist die Anzahl der Unrundheitszyklen über den Umfang. Für eine elliptische Lagerschale ist NLa=2 und für alle anderen eine natürliche Zahl größer 2.
![]()
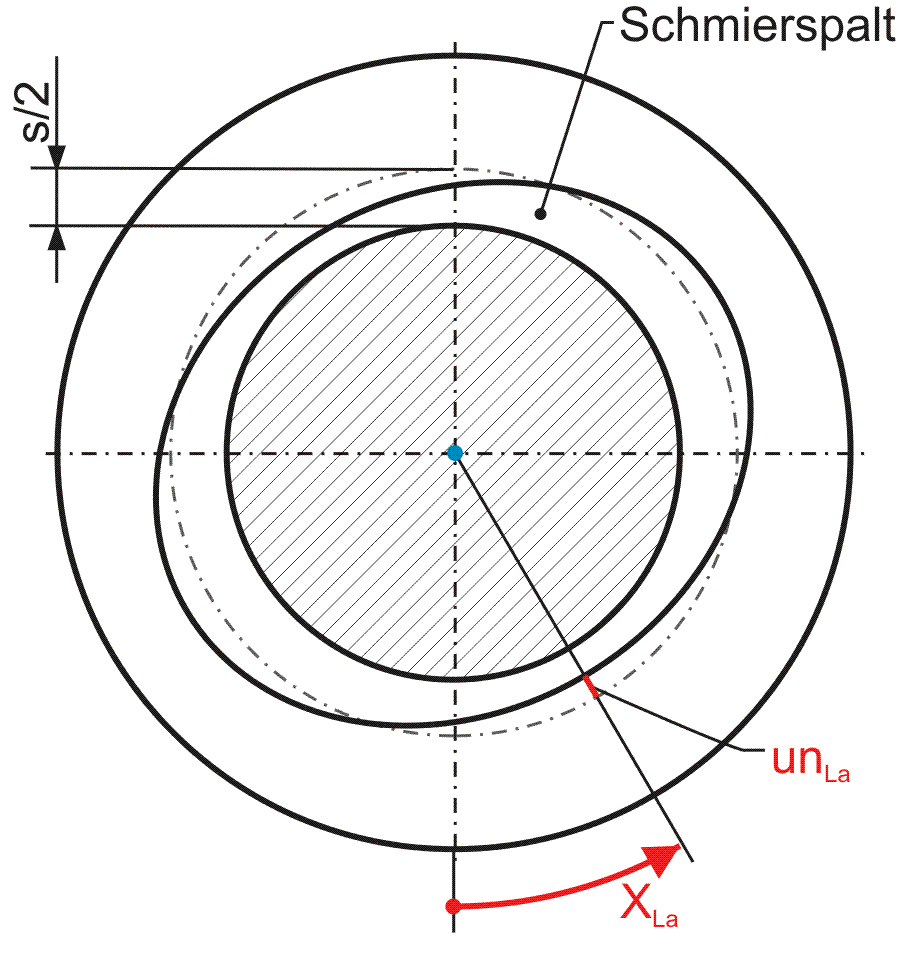
Bild 2.018: Lager mit elliptischer Lagerschale und konzentrischer ideal zylindrischer Welle
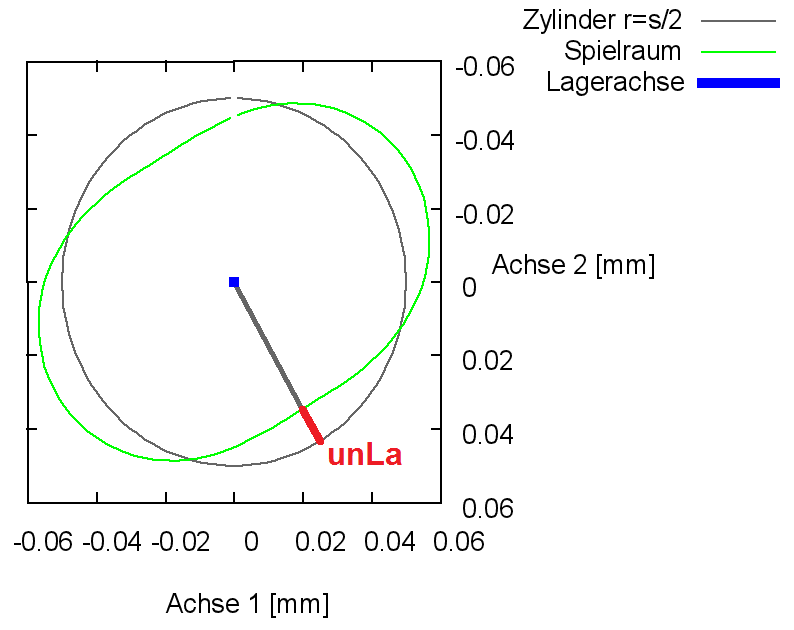
Bild 2.019 zeigt die Formabweichung des Spielraumes (grün) eines Lagers mit leicht elliptischer Lagerschale und zylindrischer Welle in einer grafischen Darstellung durch SIRIUS und GNUPLOT. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
 |
 |
Die Änderung Δh4 der Schmierspalthöhe h derartiger Formabweichungen über den Umfang der Lagerschale lassen sich durch folgende Funktion beschreiben.

Die zugehörigen partiellen Ableitungen sind dann gegeben durch

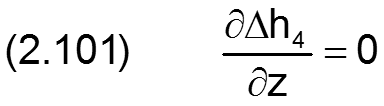
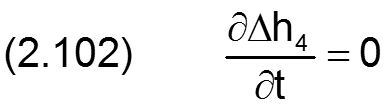
HINWEIS: Der Parameter x ist hier die dimensionsbehaftete Koordinate x des lagerschalenfesten Koordinatensystems x-y-z gemäß Bild 2.003 und nicht die Winkelangabe x in grd wie im Programm SIRIUS verwendet. XLa ist dagegen eine Winkelangabe gemessen in Radiant, die damit gleichzeitig der dimensionslosen Umfangskoordinate des Koordinatensystems X-Z im dimensionslos gemachten Lager entspricht.
Die Welle kann ebenfalls durch Fertigungsfehler leicht elliptische, "dreieckige", "viereckige" und andere "polygone" Formen bis hin zu einer welligen Oberfläche aufweisen. Derartige Formabweichungen werden in SIRIUS als zeitlich konstant angenommen, bezogen auf die bewegte Welle. Bild 2.020 zeigt als Beispiel ein Lager mit "dreieckiger" Welle. Zur Beschreibung dieser Unrundheit sind die drei Parameter unWe, XWe(t) und NWe erforderlich. Die Unrundheit unWe gibt das Maximum der Abweichung an, gemessen von einer angenommenen mittleren ideal zylindrischen Form der Welle. Die Stelle einer maximalen Abweichung XWe(t) gibt den Winkel zwischen dem Ursprung des Koordinatensystems X-z und einem Maximum der Formabweichung an, gemessen in Richtung der positiven X-Achse. Verkleinert das Maximum an der Stelle XWe die Spalthöhe wird unWe als positiver Wert angegeben, vergrößert das Maximum die Spalthöhe als negativer Wert.
![]()
NWe ist die Anzahl der Unrundheitszyklen über den Umfang. Für eine "dreieckige" Welle ist NWe=3.
![]()

Bild 2.020: Lager mit "dreieckiger" konzentrischer Welle und ideal zylindrischer Lagerschale
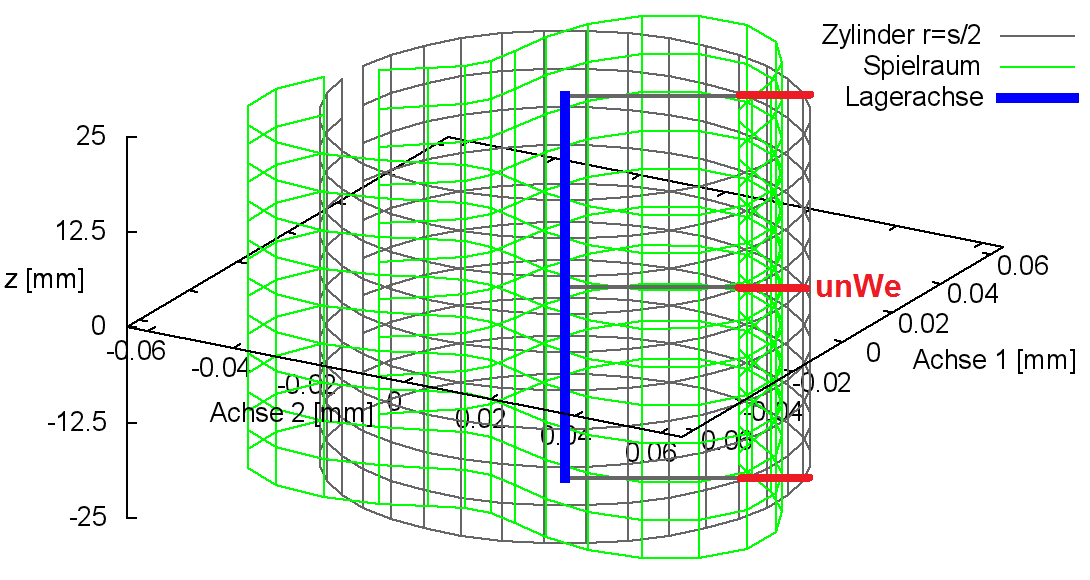
Bild 2.021 zeigt die Formabweichung des Spielraumes (grün) eines Lagers mit "dreieckiger" Welle und zylindrischer Lagerschale in einer grafische Darstellung durch SIRIUS und GNUPLOT. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
 |
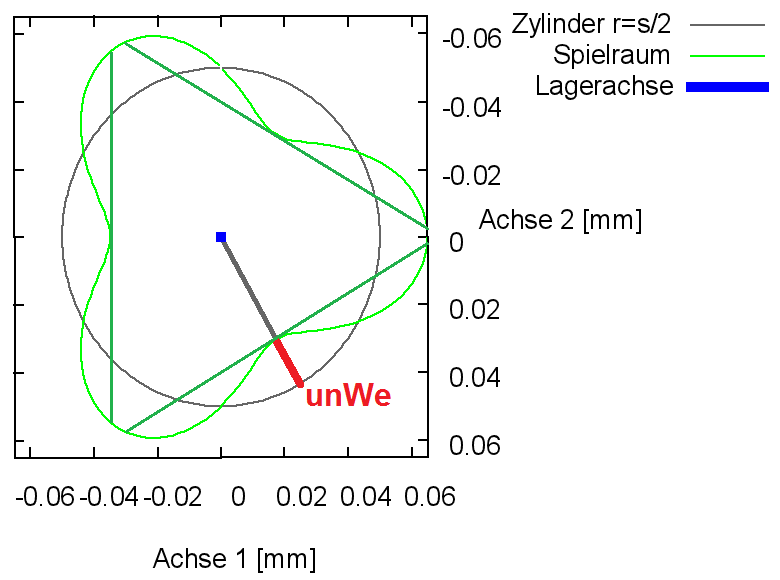 |
HINWEIS: Der Spielraum, der mit SIRIUS/Gnuplot grafisch dargestellt wird, entspricht nur so lange dem tatsächlichen Spielraum, solange der Querschnitt durch die Mantelfläche eine konvexe Geometrie aufweist. Falls dieser Querschnitt des Bildes, wie im gezeigten Beispiel, konkav ist, verkleinert sich der tatsächliche Spielraum, in dem sich die Wellenachse bewegen kann, weiter. Die in Bild 2.021 rechts eingezeichneten grünen Geraden zeigen diese weitere Einschränkung. Physikalisch bedeutet das, dass im Schmierspalt mehrere Stellen mit lokalen minimalen Schmierspalthöhen entstehen und so mehrere hydrodynamische Druckberge entstehen können, wie im Bild 2.020 gezeigt wird. Damit entsteht praktisch ein Mehrgleitflächenlager. Das gilt nicht nur für Unrundheit der Welle, sondern auch für Unrundheit der Lagerschale und deren Überlagerungen.
Weiterhin ist zu beachten, dass sich der verformte Spielraum mit der Welle mitdreht.
Die Änderung Δh5 der Schmierspalthöhe h derartiger Formabweichungen über den Umfang der Lagerschale lassen sich durch folgende Funktion beschreiben.
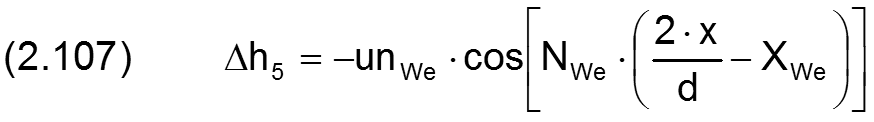
Die zugehörigen partiellen Ableitungen sind gegeben durch
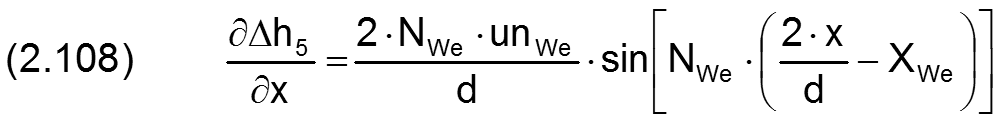
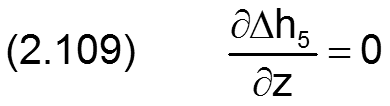

HINWEIS: Der Parameter x ist hier die dimensionsbehaftete Koordinate x des lagerschalenfesten Koordinatensystems x-y-z gemäß Bild 2.003 und nicht die Winkelangabe x in grd wie im Programm SIRIUS verwendet. XWe ist dagegen eine Winkelangabe gemessen in Radiant, die damit gleichzeitig der dimensionslosen Umfangskoordinate des Koordinatensystems X-Z im dimensionslos gemachten Lager entspricht.
Bereits bei der Überlagerung einer Unrundheit der Lagerschale und einer Unrundheit der Welle ist die Gestalt des Spielraums nicht mehr so einfach zu überschauen, denn dieser ändert mit der Drehung sowohl seine Lage als auch seine Form. Bild 2.022 zeigt als Beispiel den Spielraum (grün) in axialer Ansicht für eine "dreieckige" Welle (unWe=0,02 mm, NWe=3), die in einer elliptischen Lagerschale läuft (unLa=0,015 mm, NLa=2, s=0,1 mm, d=100 mm) zu irgend einem Zeitpunkt und in der Animation (nur HTML-Version) seine Veränderung über eine Umdrehung der Welle.
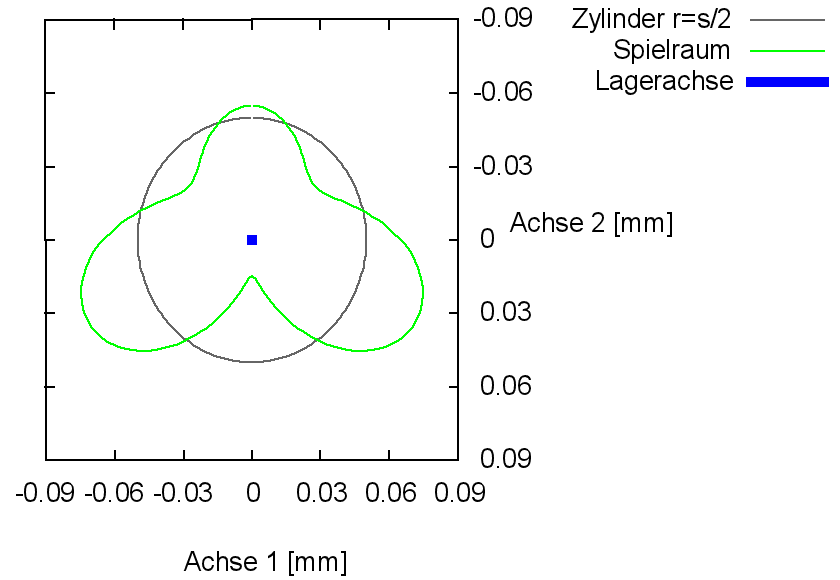
Bild 2.022: Axiale Ansicht des Spielraums eines Lagers mit elliptischer Lagerschale und "dreieckiger" Welle in konzentrischer Lage (Animation)
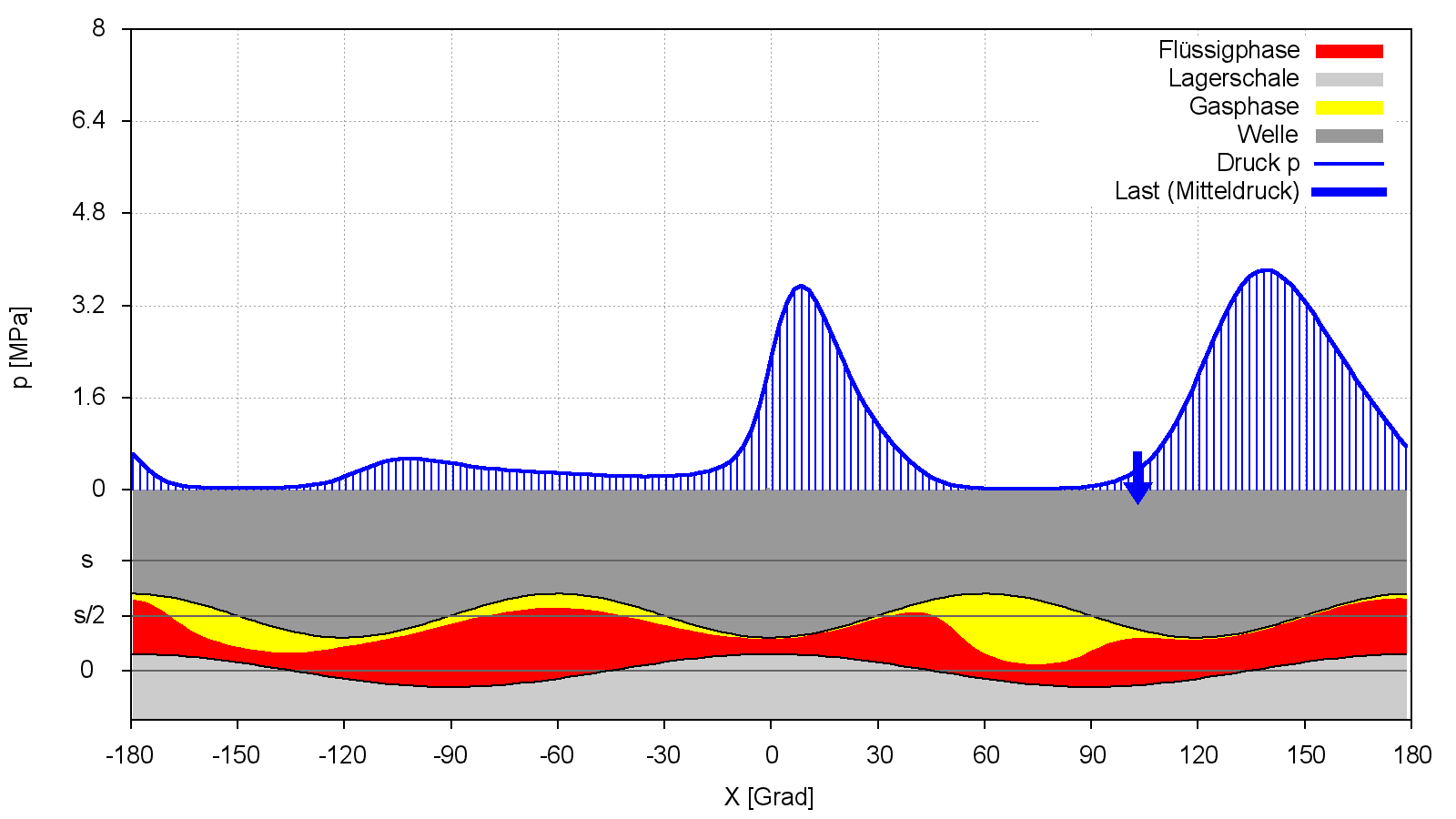
In diesem Beispiel wird angenommen, dass die Welle konzentrisch in der Lagerschale läuft. Trotzdem entwickelt sich hier im Schmierspalt bereits ein instationärer Druckverlauf p(t) mit mehreren Druckbergen, wie er in Bild 2.023 für den in Bild 2.022 gewählten Zeitpunkt und in der Animation über eine Umdrehung der Welle dargestellt ist. Das Bild 2.023 zeigt einen Querschnitt durch die Lagermitte, wobei die Spaltfläche in eine Ebene abgewickelt wurde. Der Druckverlauf wurde mit der erweiterten Reynoldsschen Gleichung berechnet. Die rote Fläche im Schmierspalt stellt den Anteil der Schmierflüssigkeit und die gelbe Fläche den Anteil der gasförmigen Phase des Schmiermittel-Gas-Gemischs dar.
Eine axiale Formabweichung des Lagers von der ideal zylindrischen Form ist eine konische Lagerschale. Die Größe der Konizität einer Lagerschale wird durch den Parameter koLa bestimmt gemäß Bild 2.024. Ein positiver Wert steht per Definition für eine Verjüngung der Lagerschale und damit für eine Verkleinerung des Schmierspalts in Richtung der positiven z-Achse. Das Lager erhält damit ein über die z-Achse linear variierendes lokales Lagerspiel. In der Lagermitte bleibt das Lagerspiel unverändert gleich dem mittleren Lagerspiel s. Das Spaltvolumen des gesamten Lagers und die mittlere Schmierspalthöhe ändern sich nicht.
Die maximale konische Formabweichung wird begrenzt auf
![]()

Bild 2.024: Lager mit konischer Lagerschale
Bild 2.025 zeigt links den Spielraum eines Lagers mit einer konischen Lagerschale mit positiver Konizität koLa und rechts den Spielraum mit negativer Konizität. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
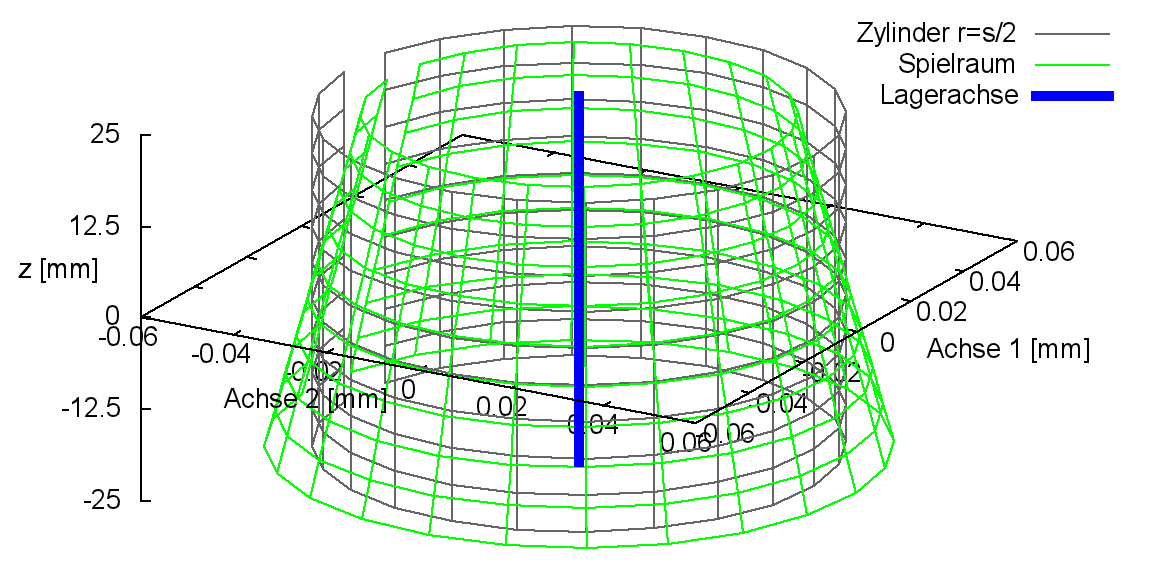 |
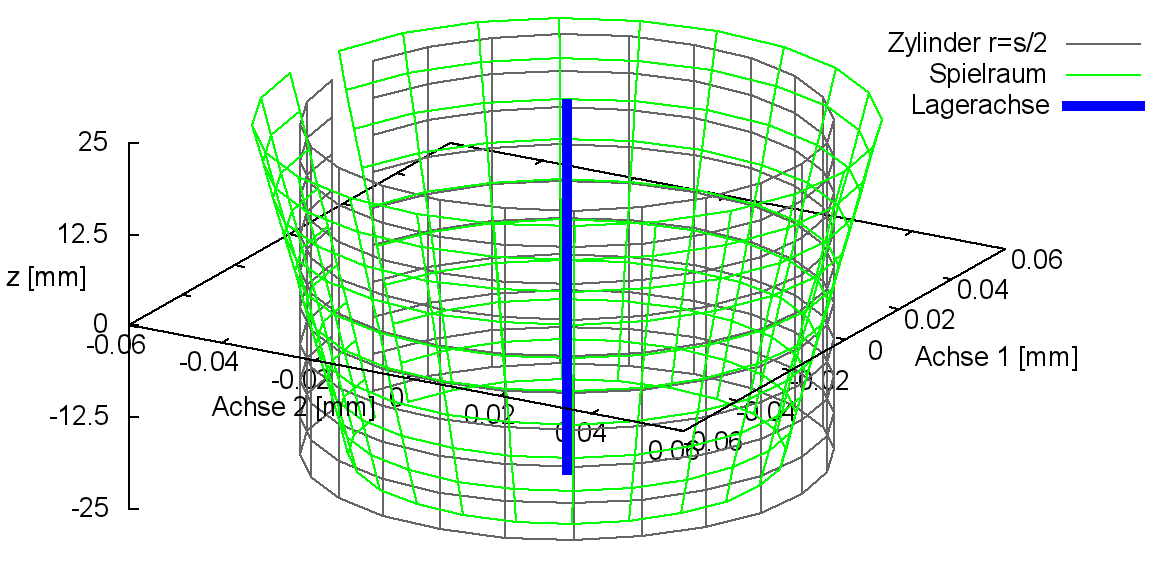 |
Die Änderung Δh6 der Schmierspalthöhe h derartiger Formabweichungen lässt sich durch folgende Formel beschreiben.
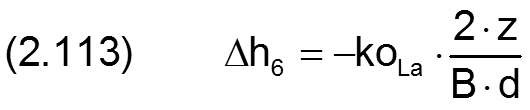
Die zugehörigen partiellen Ableitungen sind gegeben durch
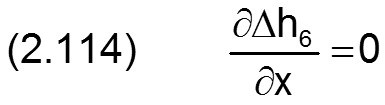
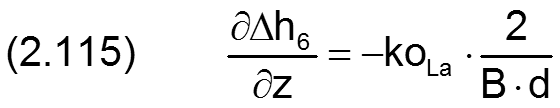
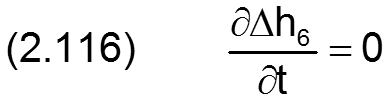
HINWEIS: Eine konische Formabweichung der Welle hat den gleichen physikalischen Effekt wie eine gleichgroße konische Formabweichung der Lagerschale. Treten sie gemeinsam auf, sind sie zu addieren. Konizität von Welle und Lagerschale gleichen Betrags mit unterschiedlichen Vorzeichen heben sich gegenseitig auf.
Eine axiale Formabweichung des Lagers von der ideal zylindrischen Form ist eine konische Welle. Die Größe der Konizität einer Welle wird durch den Parameter koWe bestimmt gemäß Bild 2.026. Ein positiver Wert steht per Definition für eine Verdickung der Welle und damit für eine Verkleinerung des Schmierspalts in Richtung der positiven z-Achse. Das Lager erhält damit ein über die z-Achse linear variierendes lokales Lagerspiel. In der Lagermitte bleibt das Lagerspiel unverändert gleich dem mittleren Lagerspiel s. Das Spaltvolumen des gesamten Lagers und die mittlere Schmierspalthöhe ändern sich nicht.
Die maximale konische Formabweichung wird begrenzt auf
![]()

Bild 2.026: Lager mit konischer Welle
Bild 2.027 zeigt links den Spielraum eines Lagers mit einer konischen Welle mit positiver Konizität koWe und rechts den Spielraum mit negativer Konizität. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
 |
 |
Die Änderung h7 der Schmierspalthöhe h derartiger Formabweichungen lässt sich durch folgende Formel beschreiben.
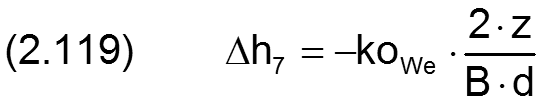
Die zugehörigen partiellen Ableitungen sind gegeben durch
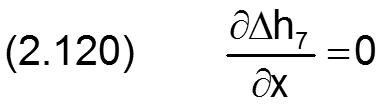
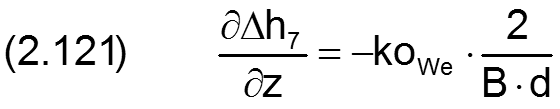
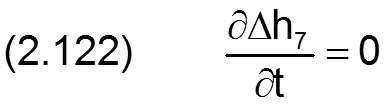
HINWEIS: Eine konische Formabweichung der Welle hat den gleichen physikalischen Effekt wie eine gleichgroße konische Formabweichung der Lagerschale. Treten sie gemeinsam auf, sind sie zu addieren. Konizität von Welle und Lagerschale gleichen Betrags mit unterschiedlichen Vorzeichen heben sich gegenseitig auf.
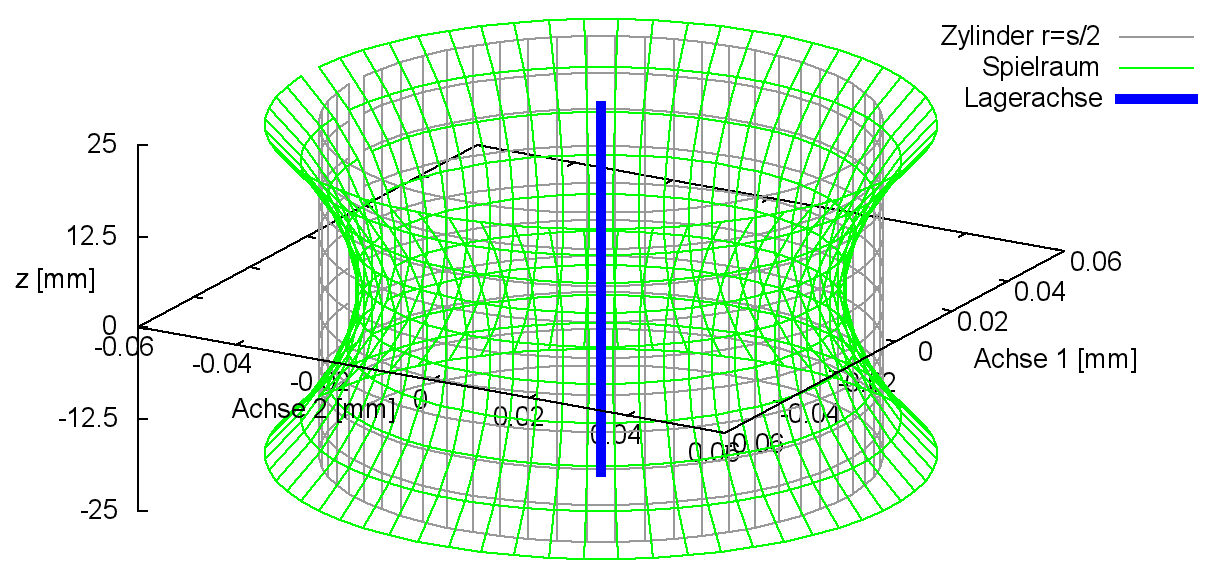
Eine weitere axiale Formabweichung des Lagers von der ideal zylindrischen Form ist eine ballige Lagerschale. Die Größe der Balligkeit einer Lagerschale wird durch den Parameter baLa bestimmt gemäß Bild 2.028. Gemäß Definition erweitert sich bei einem positiven Wert der Lagerschalen-Innendurchmesser zu den Lagerrändern hin. Damit das mittlere Lagerspiel s, die mittlere Spalthöhe und damit auch das Spaltvolumen gleich bleiben, ist die Balligkeit um den mittleren Lagerschalendurchmesser so aufgeteilt, dass der örtliche Lagerschalenradius in der Lagermitte um baLa/3 verkleinert und an den Lagerrändern um baLa·2/3 vergrößert wird.
Die maximale konische Formabweichung wird begrenzt auf
![]()
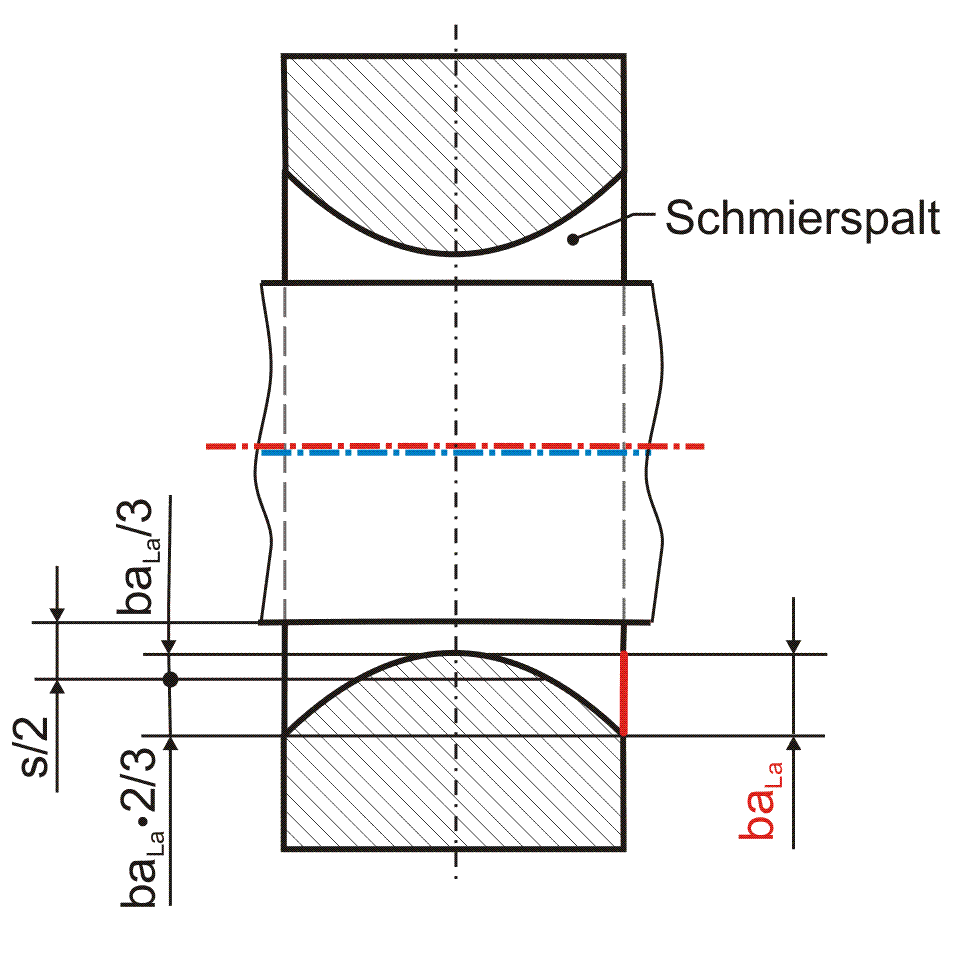
Bild 2.028: Lager mit balliger Lagerschale
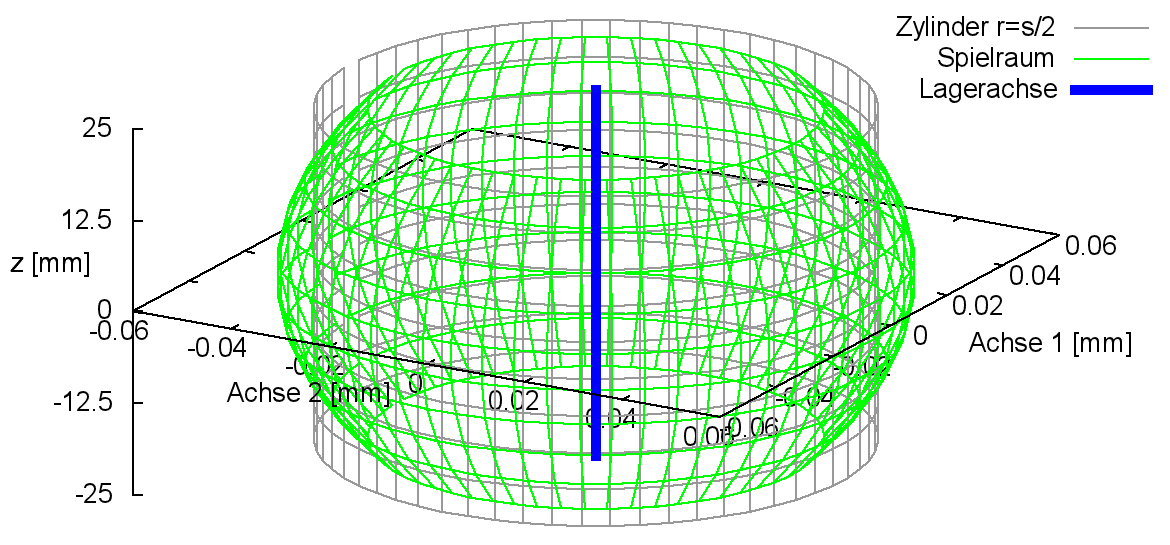
Bild 2.029 zeigt links den Spielraum (grün) eines Lagers mit einer balligen Lagerschale mit positiver Balligkeit baLa und rechts den Spielraum mit negativer Balligkeit.
 |
 |
Die Änderung Δh8 der Schmierspalthöhe derartiger Formabweichungen lässt sich durch folgende Formel beschreiben.
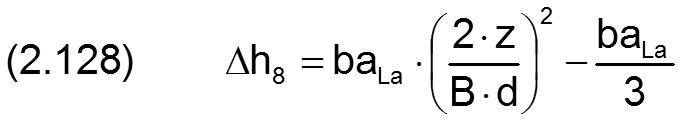
Die zugehörigen partiellen Ableitungen sind gegeben durch
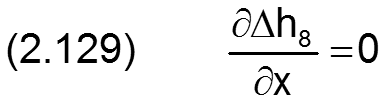
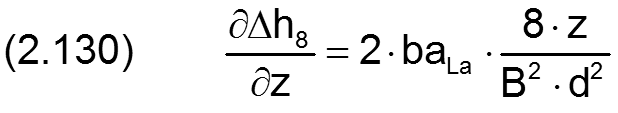
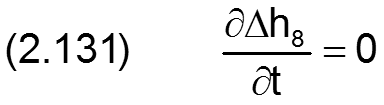
HINWEIS: Eine ballige Formabweichung der Welle hat den gleichen physikalischen Effekt wie eine gleichgroße ballige Formabweichung der Lagerschale. Treten sie gemeinsam auf, sind sie zu addieren. Balligkeit von Welle und Lagerschale gleichen Betrags mit unterschiedlichen Vorzeichen heben sich gegenseitig auf.
Eine weitere axiale Formabweichung des Lagers von der ideal zylindrischen Form ist eine ballige Welle. Die Größe der Balligkeit einer Welle wird durch den Parameter baWe bestimmt gemäß Bild 2.030. Gemäß Definition verringert sich bei einem positiven Wert der Wellendurch-messer zu den Lagerrändern hin. Damit das mittlere Lagerspiel s, die mittlere Spalthöhe und damit auch das Spaltvolumen gleich bleiben, ist die Balligkeit um den mittleren Wellendurchmesser so aufgeteilt, dass der örtliche Wellenradius in der Lagermitte um baWe/3 vergrößert und an den Lagerrändern um baWe·2/3 verkleinert wird.
Die maximale konische Formabweichung wird begrenzt auf
![]()
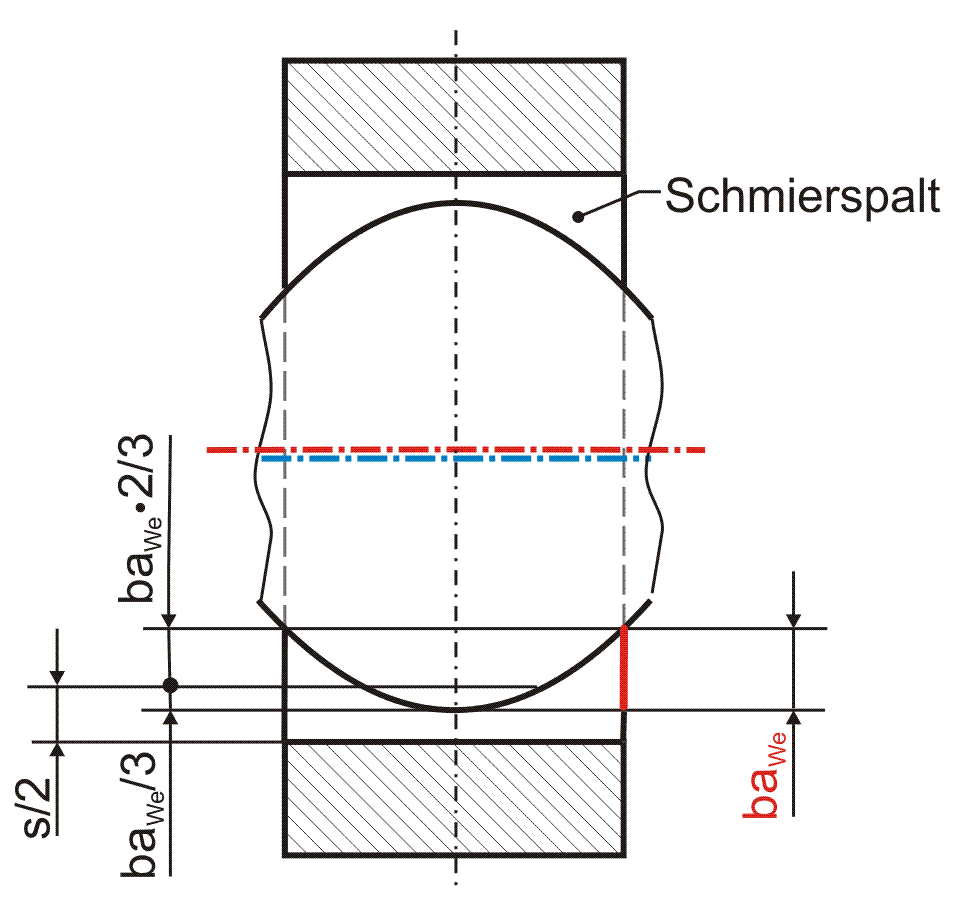
Bild 2.030: Lager mit balliger Welle
Bild 2.031 zeigt links den Spielraum (grün) eines Lagers mit einer balligen Welle mit positiver Balligkeit baWe und rechts den Spielraum mit negativer Balligkeit.
 |
 |
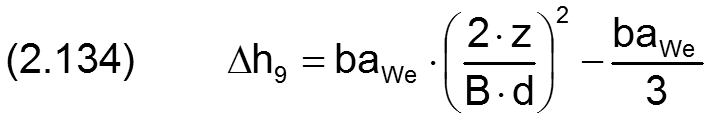
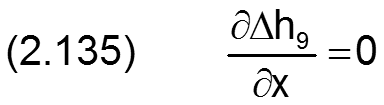
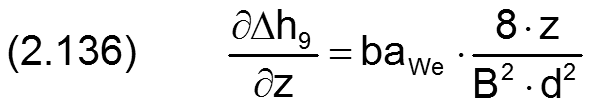
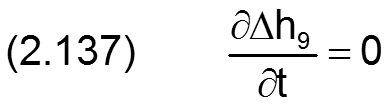
HINWEIS: Eine ballige Formabweichung der Welle hat den gleichen physikalischen Effekt wie eine gleichgroße ballige Formabweichung der Lagerschale. Treten sie gemeinsam auf, sind sie zu addieren. Balligkeit von Welle und Lagerschale gleichen Betrags mit unterschiedlichen Vorzeichen heben sich gegenseitig auf.
Mit der Variante "Lagerversatz" wurde ein Spezialfall der Lagergeometrie in das Programm SIRIUS implementiert. Er beruht auf der Idee, mit diesem Versatz bei Gleitgelenken mit einer pendelnden Drehbewegung den hydrodynamischen Druckaufbau und damit die Tragfähigkeit des Gleitgelenks zu erhöhen. Siehe dazu auch [21]. Außerdem dient dieser Spezialfall als ein Demonstrationsbeispiel, das zeigt, wie das Baukastensystem des Programms SIRIUS erweitert werden kann.
Das Bild 2.032 zeigt die 2 möglichen Varianten.
 |
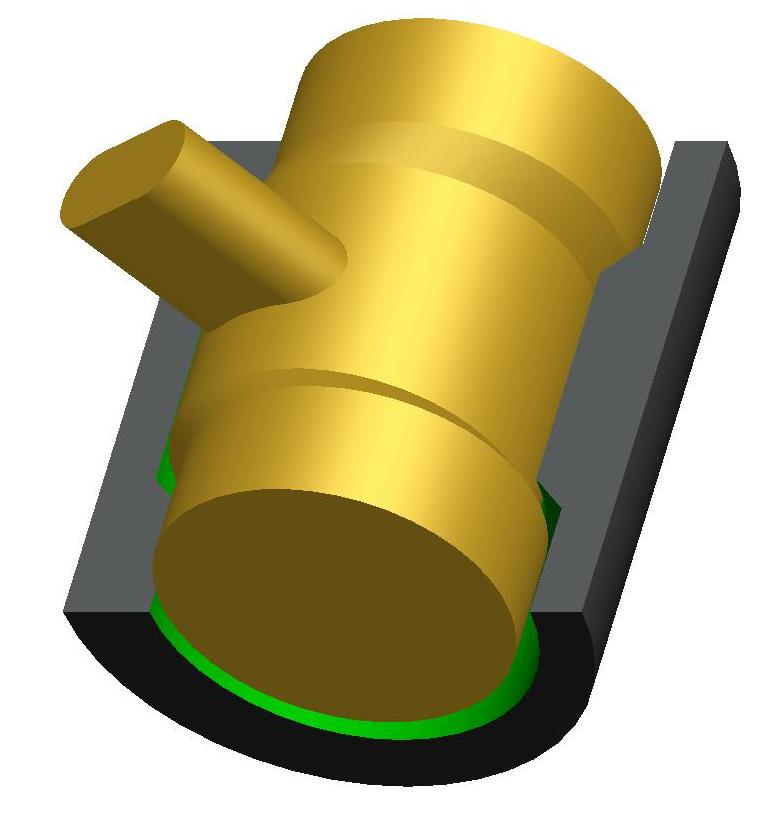 |
Hier besteht sowohl die Welle als auch die Lagerschale aus 2 bzw. 3 zueinander versetzten Abschnitten und dazwischen entsprechenden Übergängen. Dadurch wird bei einer pendelnden Drehbewegung erreicht, dass während eines Pendelzyklusses mal der eine Lagerabschnitt entlastet wird und mal der andere. In der Entlastungsphase erweitert sich der Schmierspalt und kann durch entsprechende Schmiertaschen wieder mit Schmiermittel gefüllt werden. In der Belastungsphase verringert sich die Spalthöhe und es baut sich ein hydrodynamischer Schmierfilmdruck auf. Damit beruht die Tragfähigkeit des Gleitgelenks auf einer Verdrängungswirkung. So ist das Lager nicht auf die Keilwirkung durch die Wellenrotation angewiesen, die bei pendelnden Drehungen gering ist. Die Variante mit nur 2 versetzten Lagerabschnitten zielt darauf ab mit großflächigen Lagerabschnitten eine möglichst große Tragfähigkeit zu erreichen. Die Variante mit 3 versetzten Lagerabschnitten zielt darauf ab, einen symmetrischen Druckaufbau im Lager zu erreichen und damit die Entstehung eines Kippmoments zu vermeiden. Eine weitere Unterteilung in noch mehr Lagerabschnitte scheint nicht sinnvoll, weil damit die realisierbare Tragfähigkeit sinkt.
Die Bilder 2.033 und 2.034 zeigen die notwendigen Parameter mit denen der Achsversatz der Lagerabschnitte für die Lagerschale und die Welle definiert wird. Zur besseren Übersicht sind Welle und Lagerschale getrennt dargestellt.
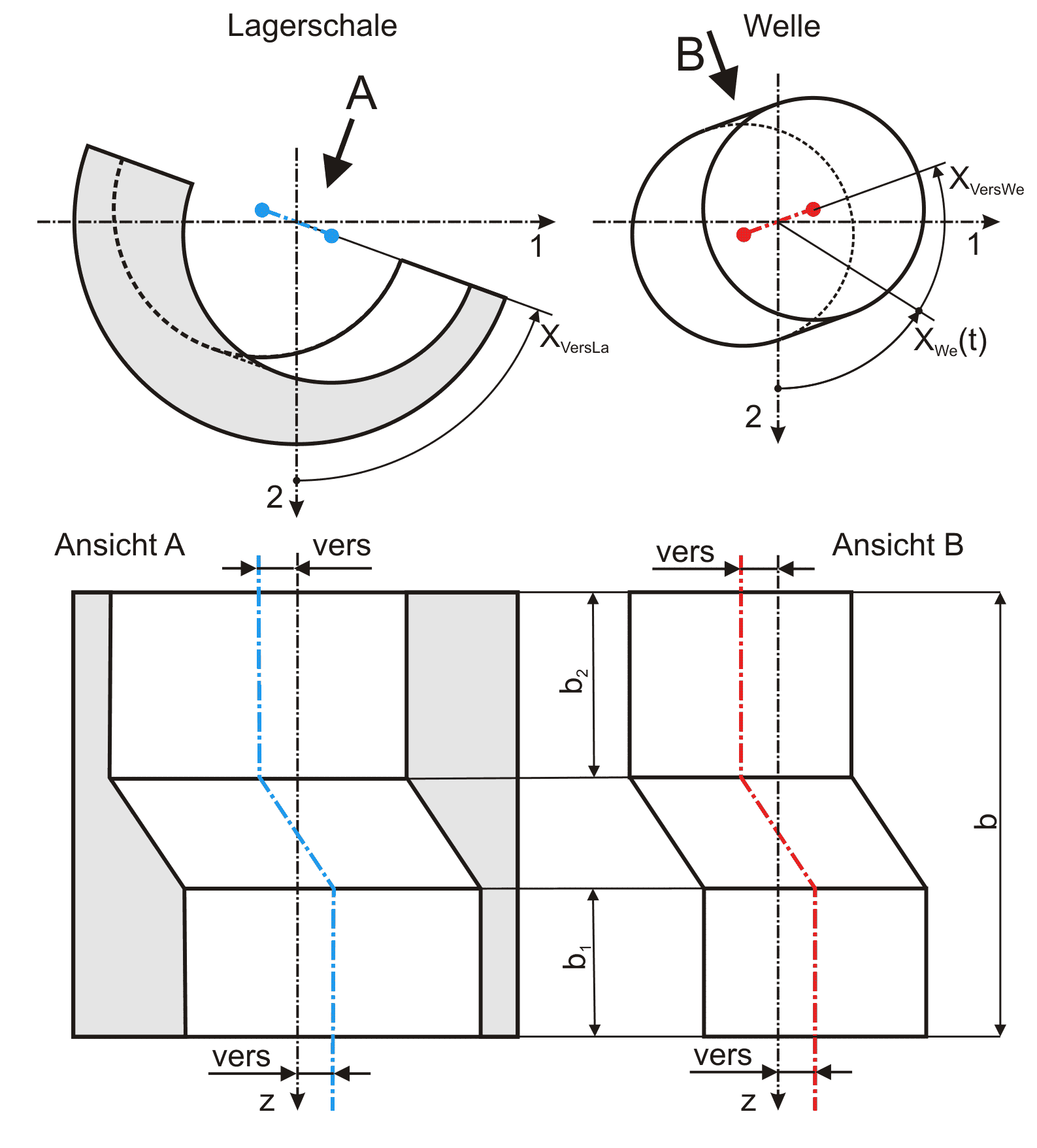
Bild 2.033: Definition der Parameter bei 2 versetzten Lagerabschnitten, links: Lagerschale, rechts: Welle
Welle und Lagerschale haben den gleichen Achsversatz vers und die entsprechenden Wellen- und Lagerschalenabschnitte haben jeweils die gleichen Breiten b1 bzw. b2. b1 und b2 können ungleich sein. Die Lage der Ebene des Achsversatzes der Lagerschale wird durch den Winkel XVersLa beschrieben (Siehe Bild 2.033, linke Ansicht). Die Lage der Ebene des Achsversatzes der Welle ist zeitabhängig und wird durch den zeitabhängigen Drehwinkel der Welle XWe(t) und den zeitlich konstanten Winkel XVersWe bestimmt (Siehe Bild 2.033, rechte Ansicht). Damit wird der Achsversatz durch 6 Parameter beschrieben.
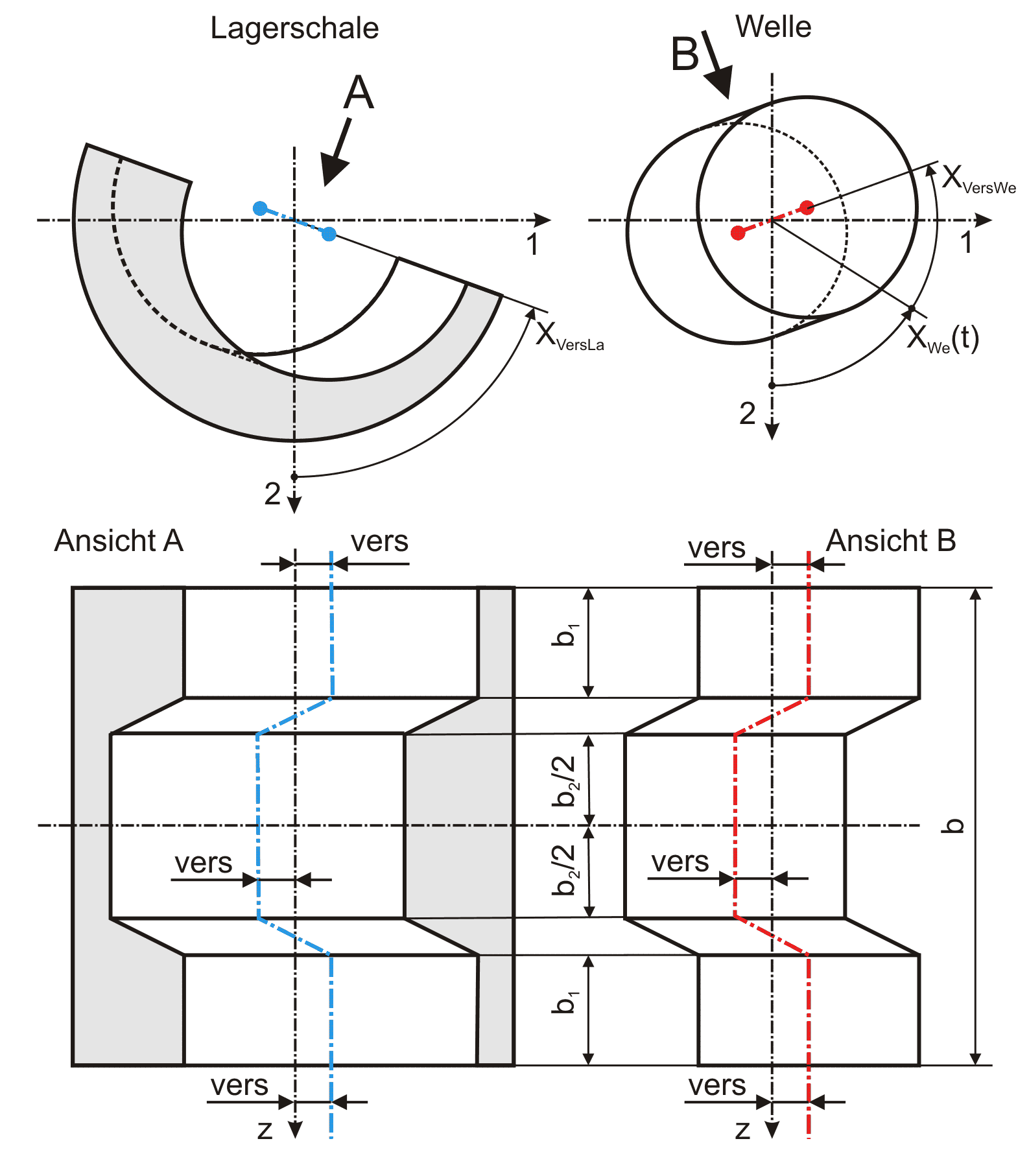
Bild 2.034: Definition der Parameter bei 3 versetzten Lagerabschnitten
Bei der Variante mit 3 versetzten Lagerabschnitten (Bild 2.034) wird außerdem angenommen, dass die Aufteilung der Lagerabschnitte symmetrisch ist.
Beschreibung der Parameter:
| vers | Abstand zwischen der Achse eines versetzten Lagerabschnitts und der gedachten mittleren Achse der Welle bzw. der Lagerschale (Achsversatz) |
| b1 | Breite des versetzten Lagerabschnitts am Lagerende in positive Richtung der z-Achse des Koordinatensystems x-y-z bei der Variante mit nur 2 versetzten Lagerabschnitten bzw. Breite der beiden Lagerabschnitte an den Lagerrändern bei 3 versetzten Lagerabschnitten. |
| b2 | Breite des versetzten Lagerabschnitts am Lagerende in negative Richtung der z-Achse bei der Variante mit nur 2 versetzten Lagerabschnitten bzw. Breite des versetzten mittleren Abschnitts bei 3 versetzten Lagerabschnitten. |
| XVersLa | Winkel zwischen der Ebene 2-3 des Koordinatensystems 1-2-3 und der Ebene, in der die gedachte gerade mittlere Lagerschalenachse und die Achsen der versetzten Lagerschalenabschnitte liegen. |
| XVersWe | Winkel zwischen der Ebene 2-3 des Koordinatensystems 1-2-3 und der Ebene, in der die gedachte gerade mittlere Wellenachse und die Achsen der versetzten Wellenabschnitte liegen. |
| XWe(t) | Drehwinkel der Welle (Siehe dazu Abschnitt 2.1.1.4) |
Es müssen für jeden Lagerabschnitt und die Übergänge gesonderte Formeln hergeleitet werden. Gemäß Bild 2.035 ergeben sich dabei 5 verschiedene Fälle.
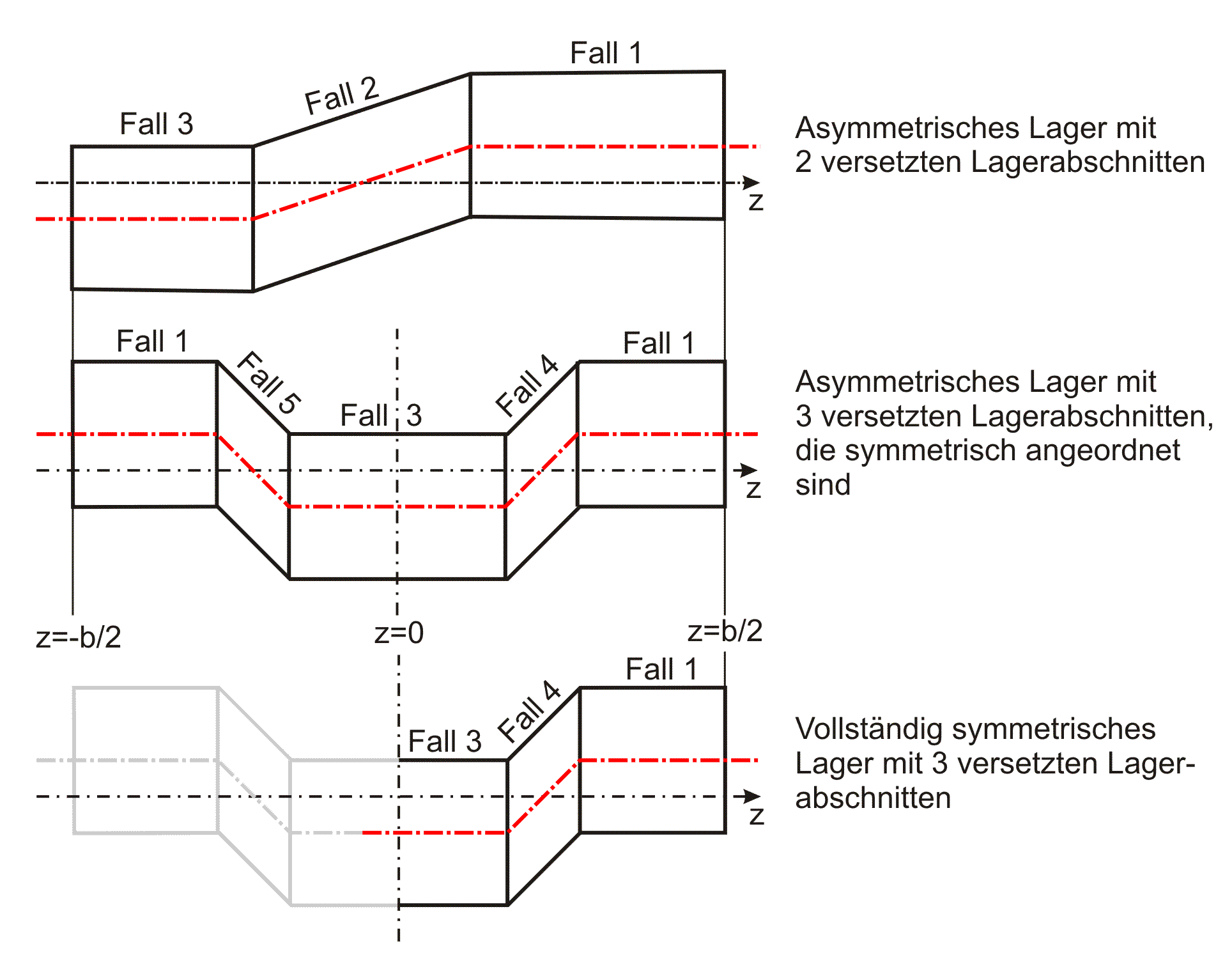
Bild 2.035: Zuordnung der Formeln zur Berechnung der Formabweichungen Δh10 zu den verschiedenen Lagerabschnitten und Übergängen
Die Änderung Δh10 der Schmierspalthöhe über die Spaltfläche und die Zeit derartiger Formabweichungen lassen sich durch folgende Formeln beschreiben.
Fall 1:
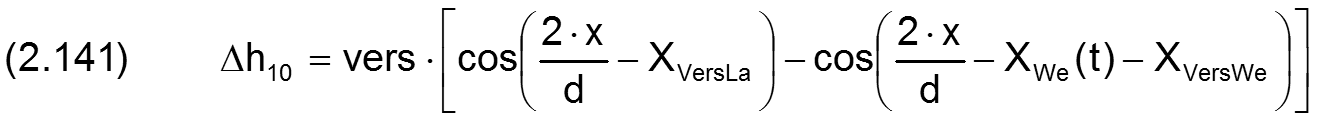
Die zugehörigen partiellen Ableitungen sind gegeben durch
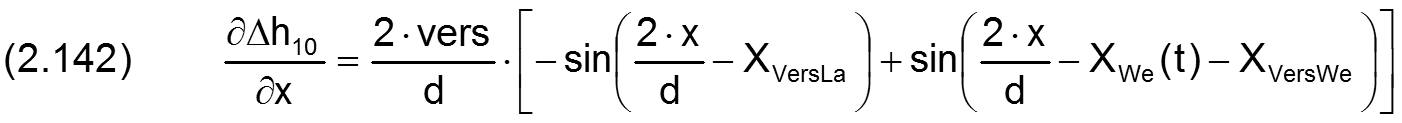
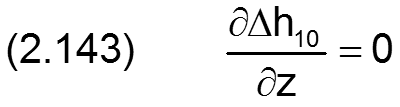
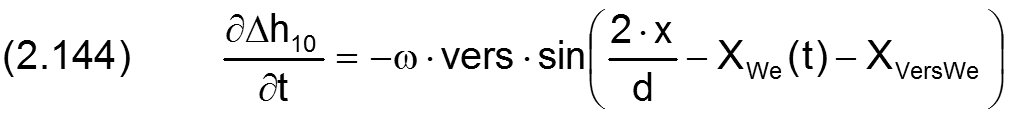
Fall 2:
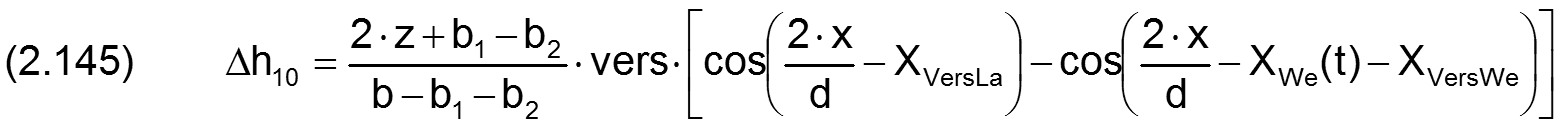
Die zugehörigen partiellen Ableitungen sind gegeben durch
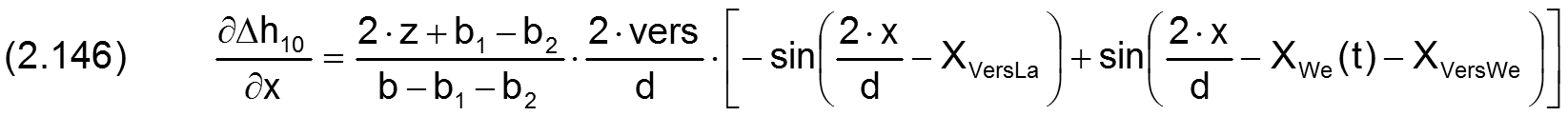
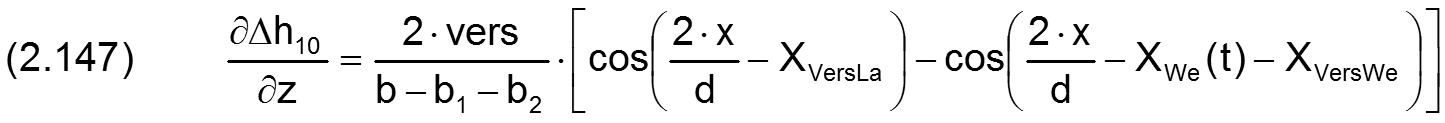

Fall 3:

Die zugehörigen partiellen Ableitungen sind gegeben durch
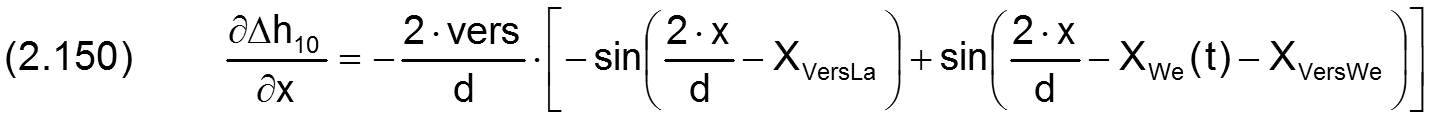
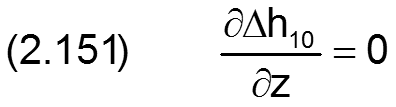
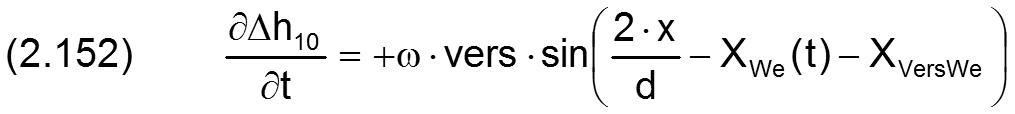
Fall 4:
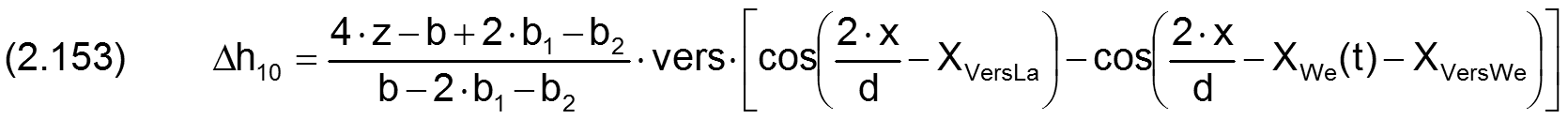
Die zugehörigen partiellen Ableitungen sind gegeben durch
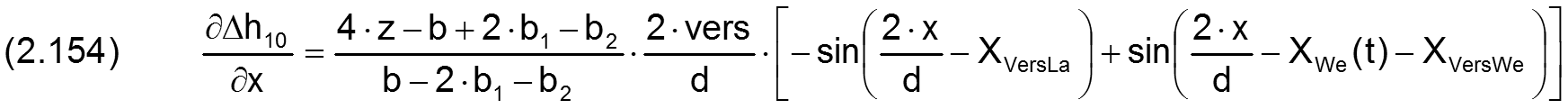
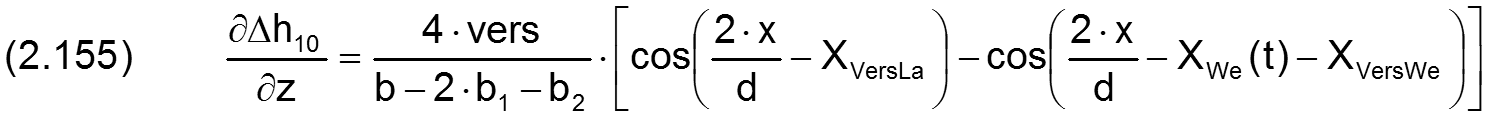
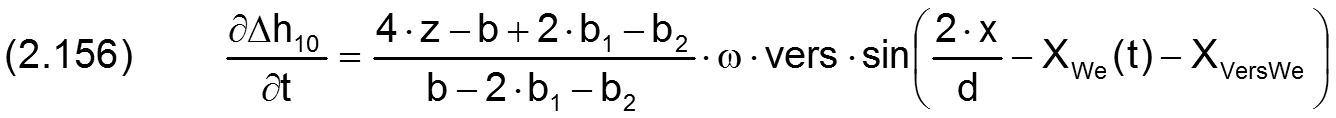
Fall 5:
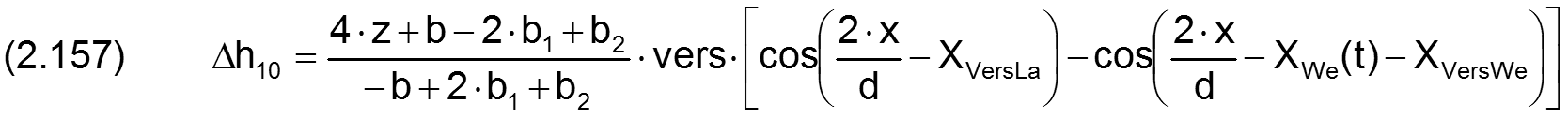
Die zugehörigen partiellen Ableitungen sind gegeben durch

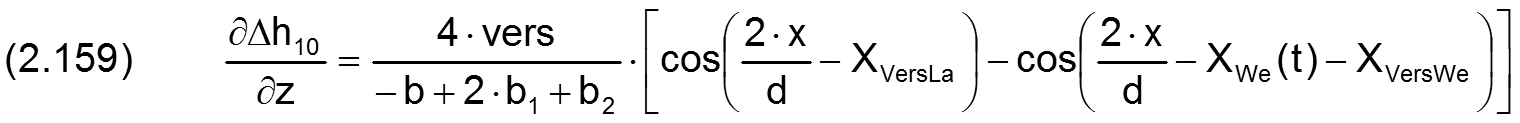
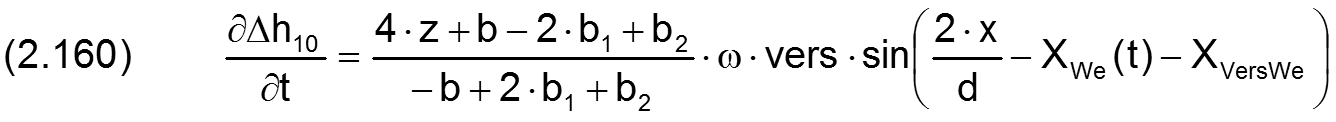
Siehe hierzu auch das Demonstrationsbeispiel DemoX15 (Abschnitt 4.8.14).
Da die Spalthöhe h analog dem Lagerspiel s viel keiner ist als der Wellendurchmesser d, können die verschiedenen Formabweichungen beliebig überlagert werden, indem diese und auch ihre partiellen Ableitungen einfach addiert werden.
So ist die aus allen definierten Verlagerungen und Formabweichungen resultierende Spalthöhe h(x,z,t) gegeben durch
![]()
Durch einsetzen der Gleichungen (2.027), (2.035), (2.056), (2.079), (2.090), (2.107), (2.113), (2.119), (2.128) und (2.134) ergibt sich die ausgeschriebene Gleichung für die Spalthöhe h
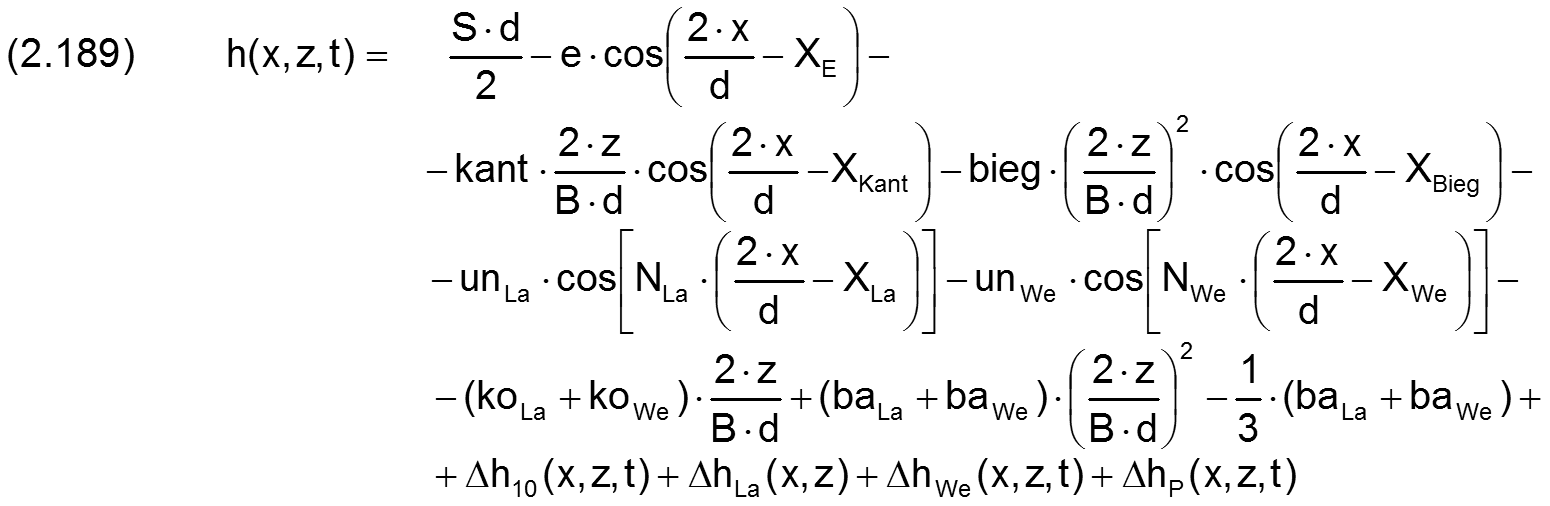
Die zugehörige partielle Ableitung ∂h/∂x ist gegeben durch

Durch einsetzen der Gleichungen (2.036), (2.057), (2.080), (2.100), (2.108), (2.114) und (2.120) ergibt sich die ausgeschriebene Gleichung
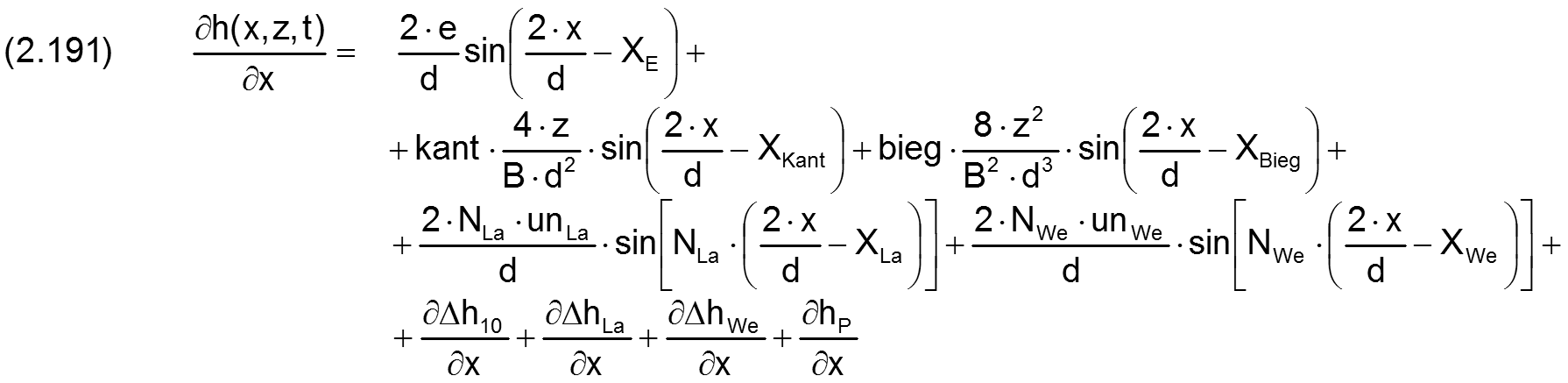
Die zugehörige partielle Ableitung ∂h/∂z ist gegeben durch
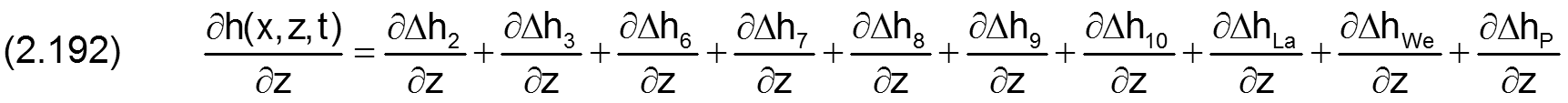
Durch einsetzen der Gleichungen (2.058), (2.081), (2.115), (2.121), (2.130) und (2.136) ergibt sich die ausgeschriebene Gleichung
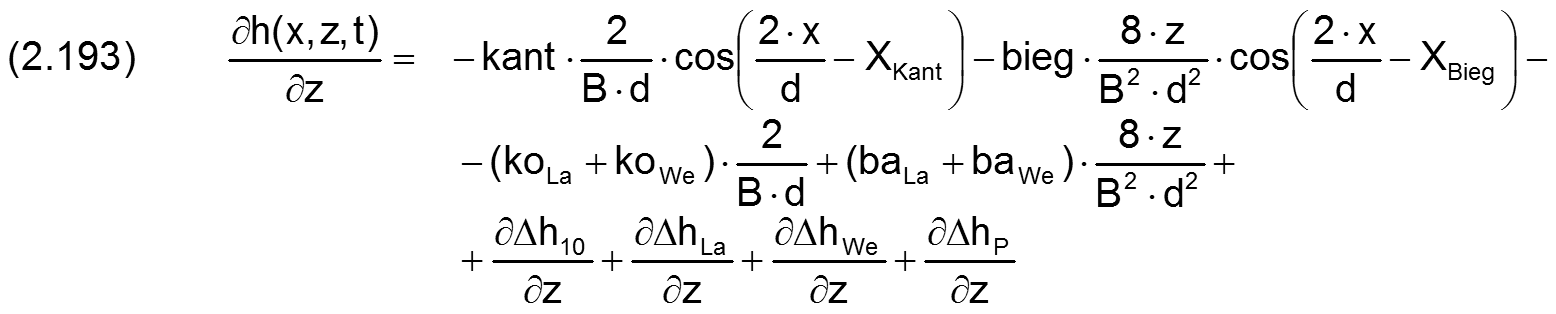
Die zugehörige partielle Ableitung ∂h/∂t ist gegeben durch
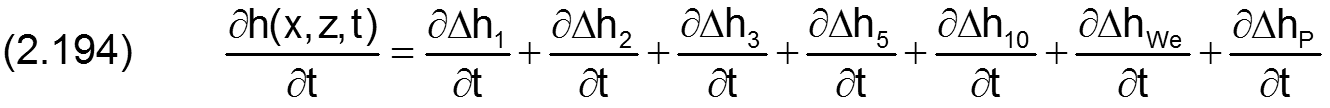
Durch einsetzen der Gleichungen (2.038), (2.059), (2.082), und (2.110) ergibt sich die ausgeschriebene Gleichung
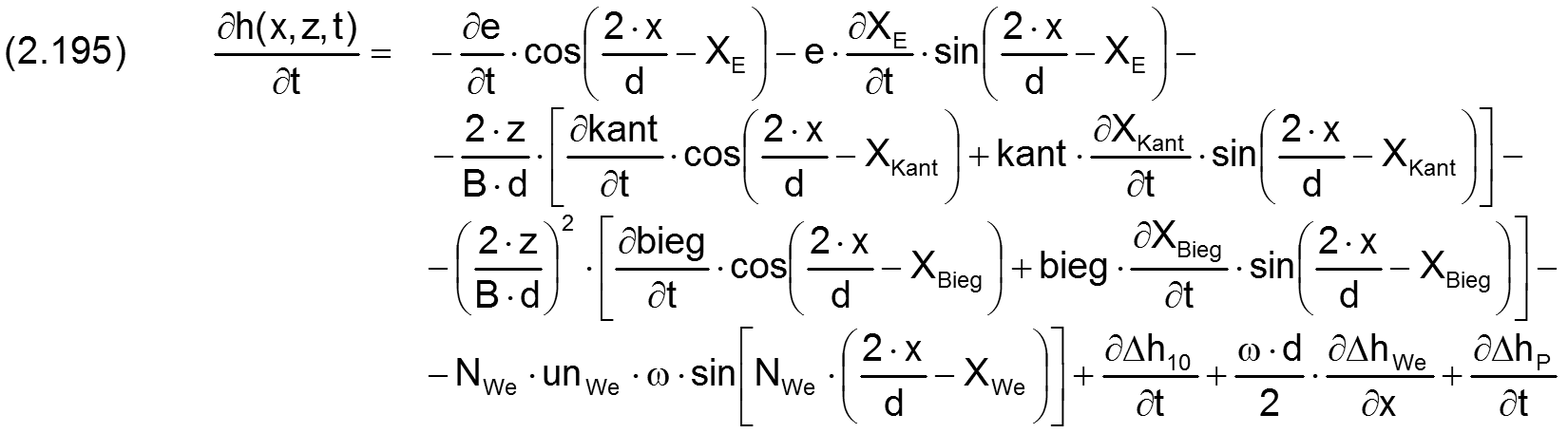
Das Gesamtvolumen volSpalt des Schmierspalts wird berechnet durch
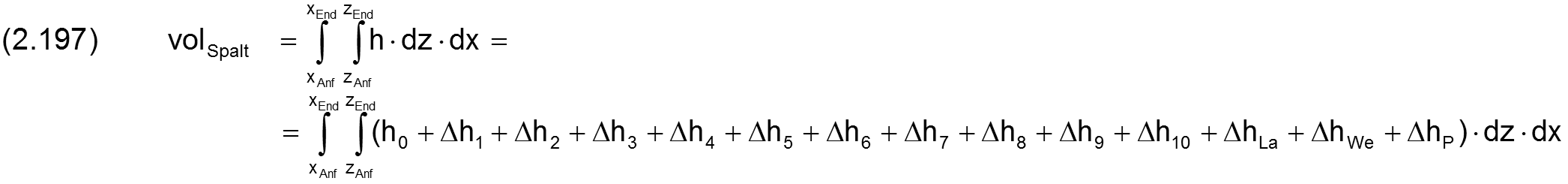
Bei einem nur teilweise umschlossenen Lager verändert sich das Spaltvolumen über die Zeit durch Veränderung der Lage der Welle zur Lagerschale. Außerdem kann sich das Spaltvolumen durch eine elastische Verformung ΔhP der Lagerschale verändern.
Bei Annahme eines voll umschlossenen, starren Lagers ist das Spaltvolumen über die Zeit konstant und die Formel für das Spaltvolumen vereinfacht sich.
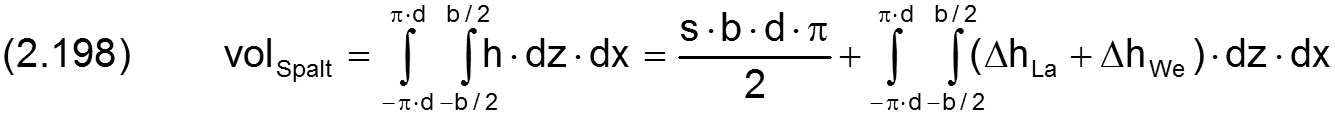
Sind keine beliebigen punktweise gegebenen Formabweichungen der Lagerschale oder der Welle gegeben, bzw. sind diese so angegeben, dass das angegebene Lagerspiel s auch weiterhin das mittlere Lagerspiel ist, dann vereinfacht sich die Formel für das voll umschlossenen Lager weiter.
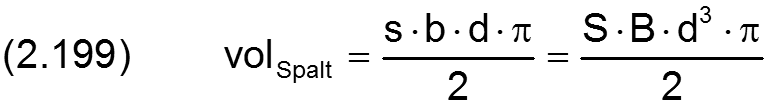
zurück weiter
.
.
.