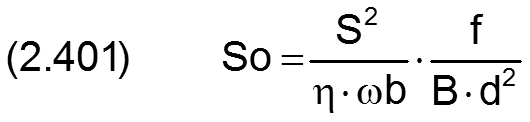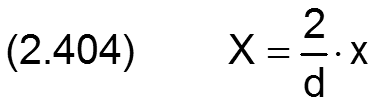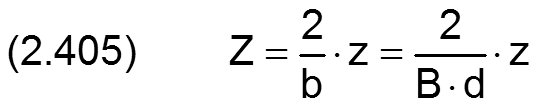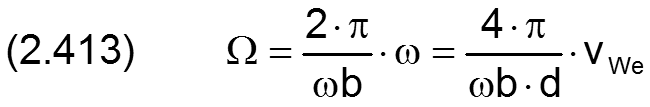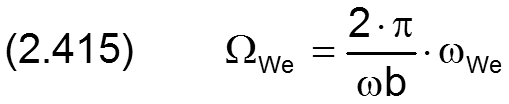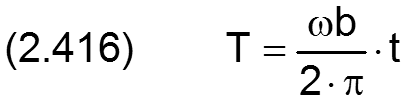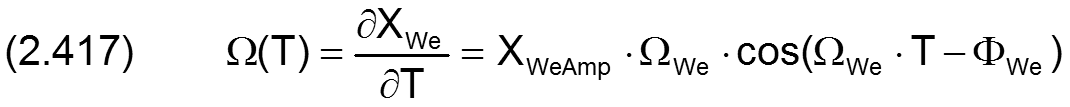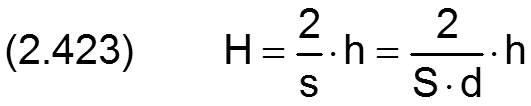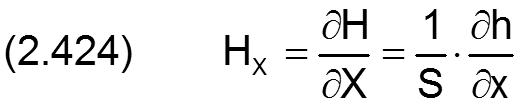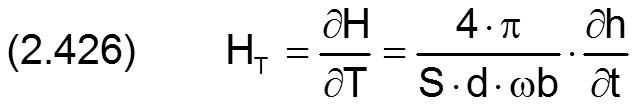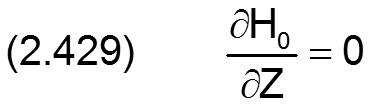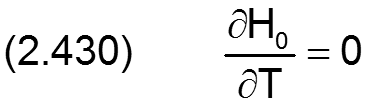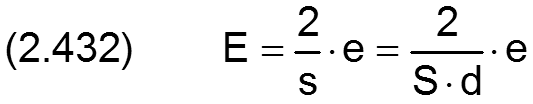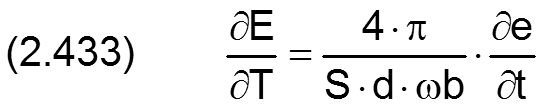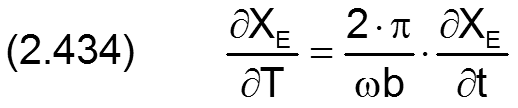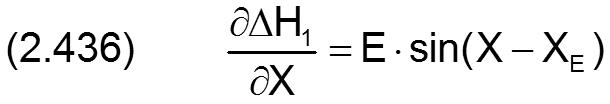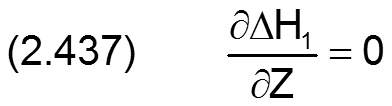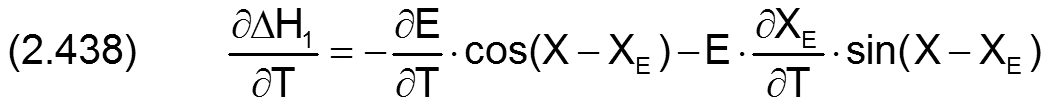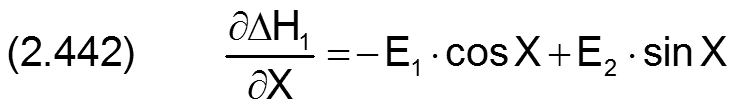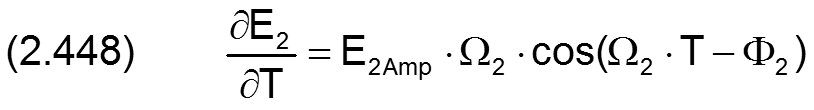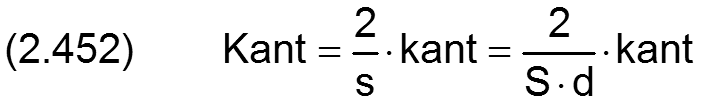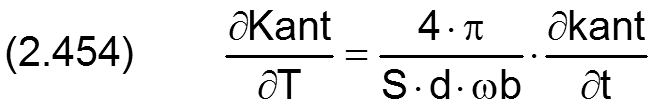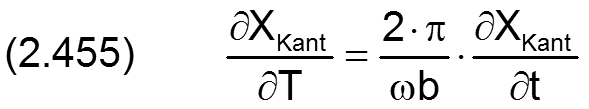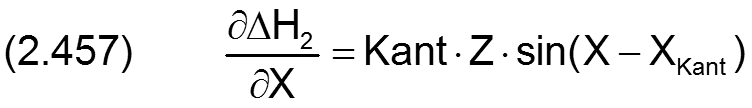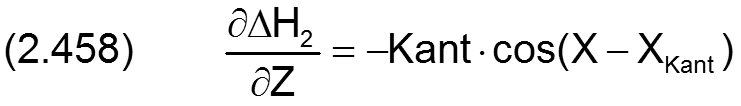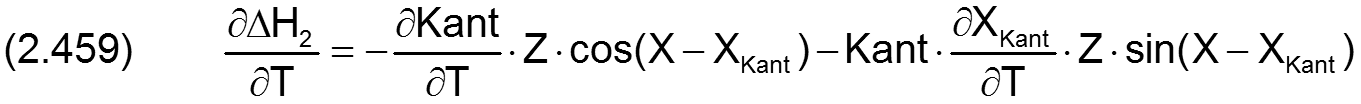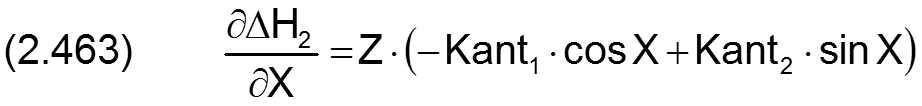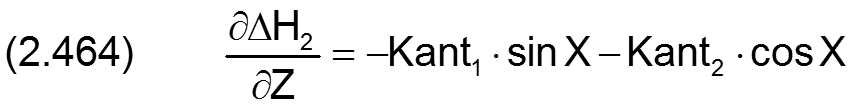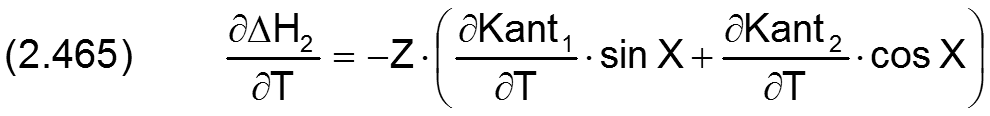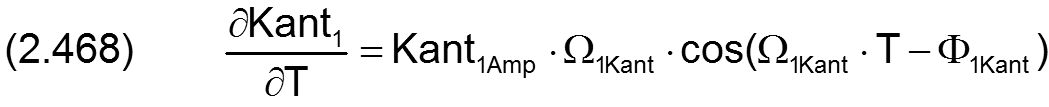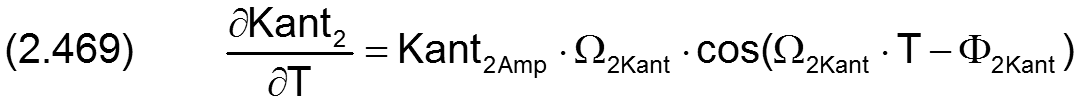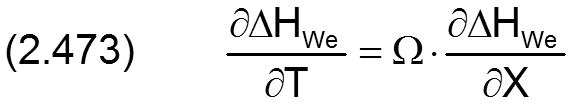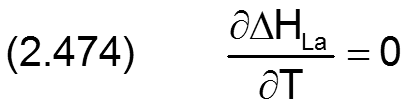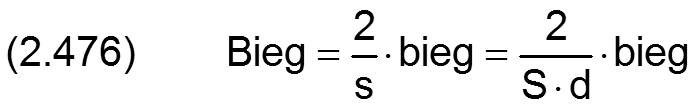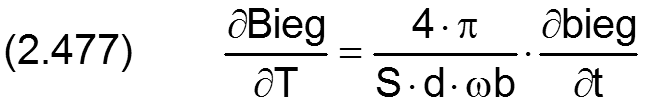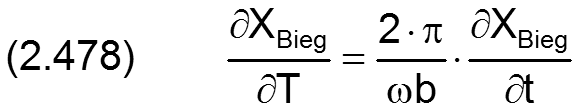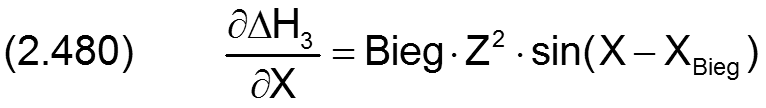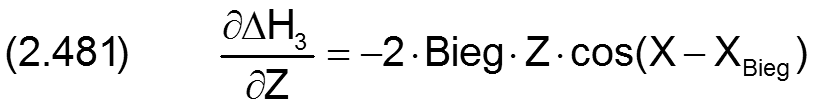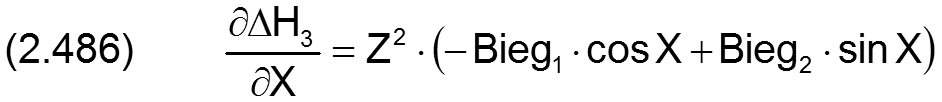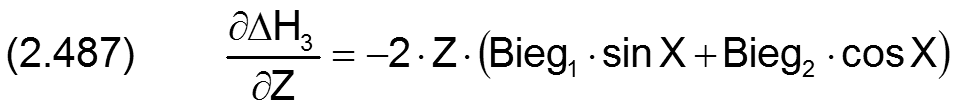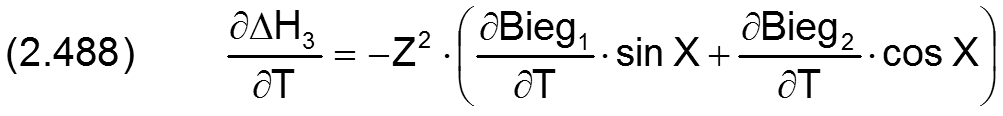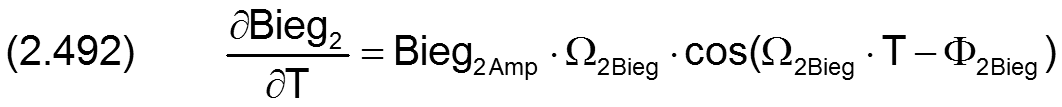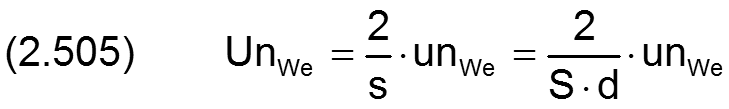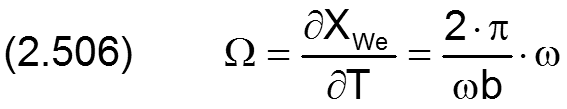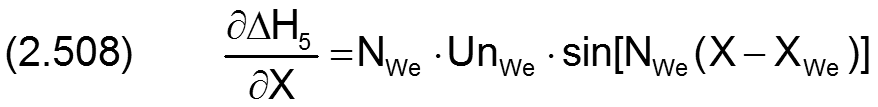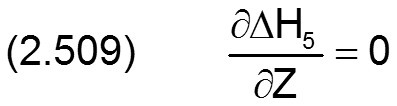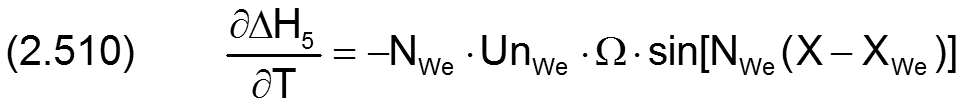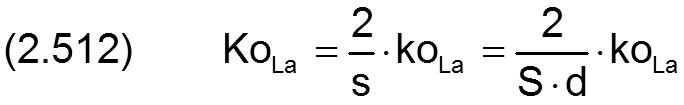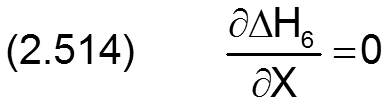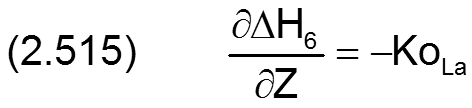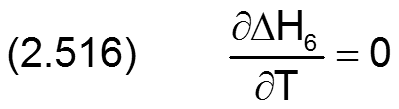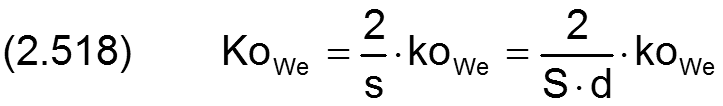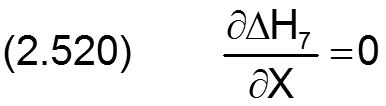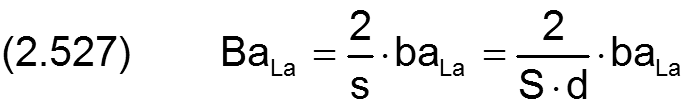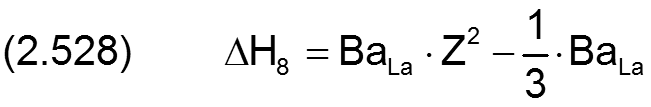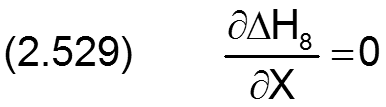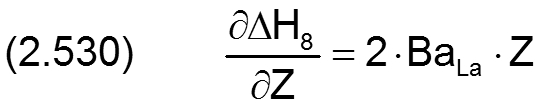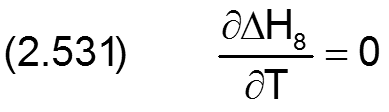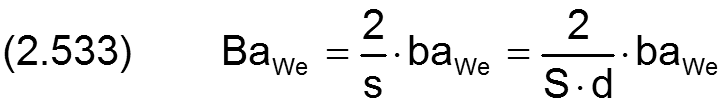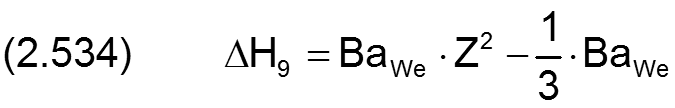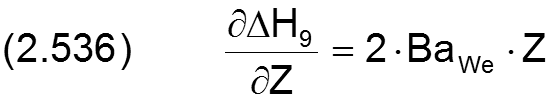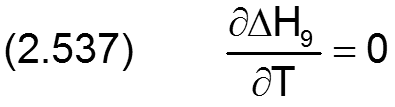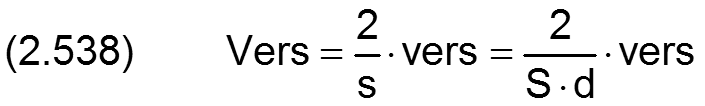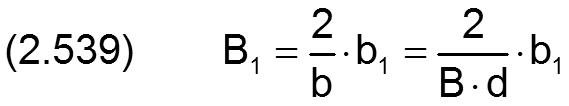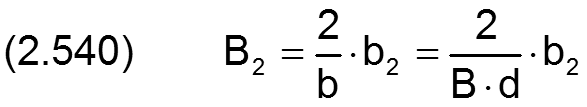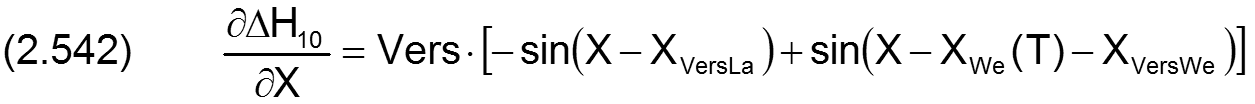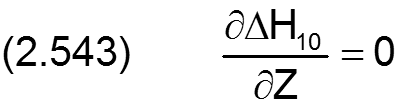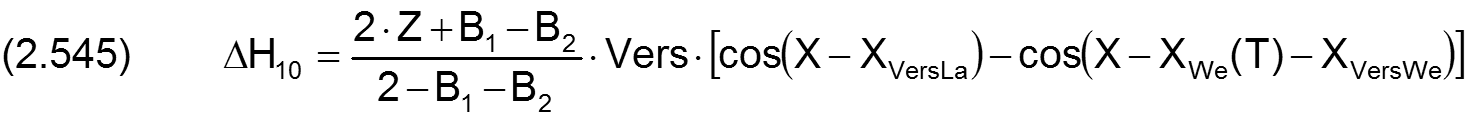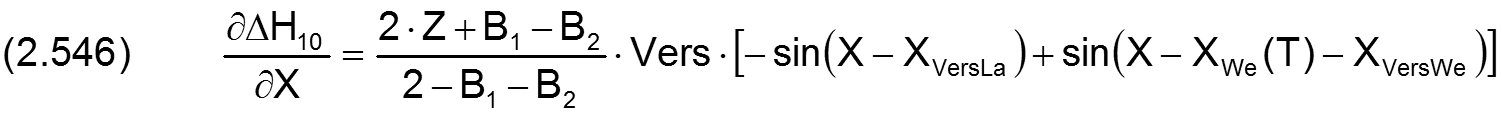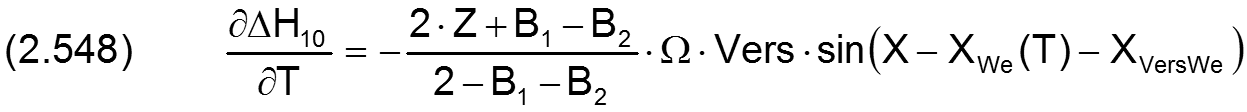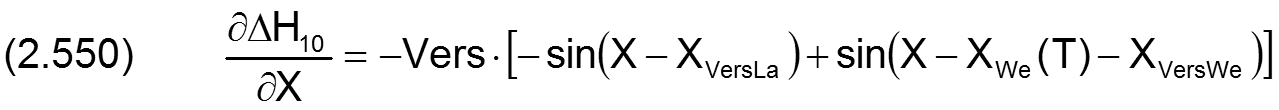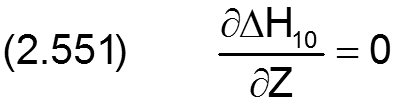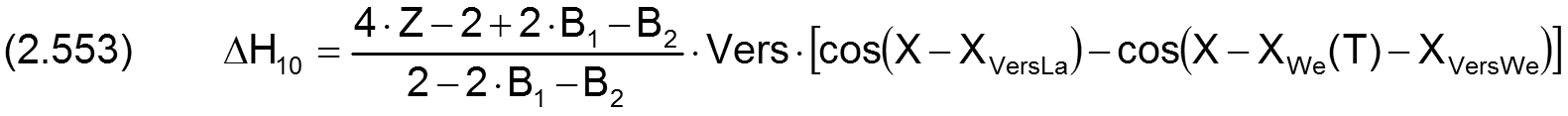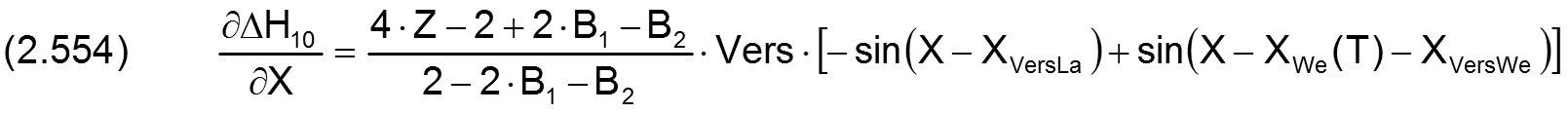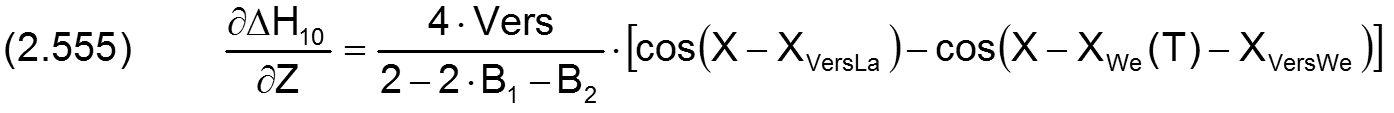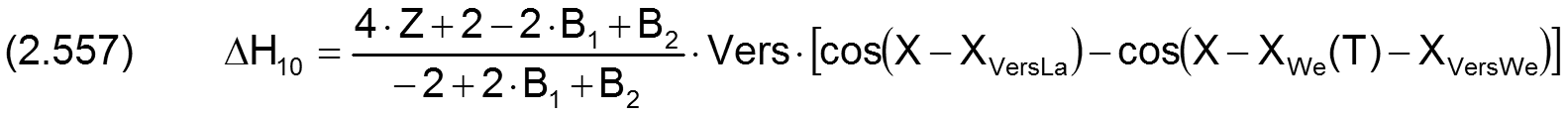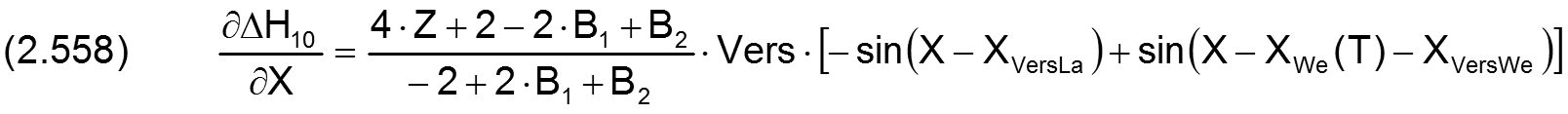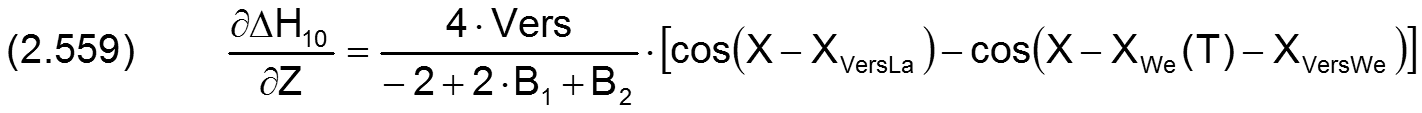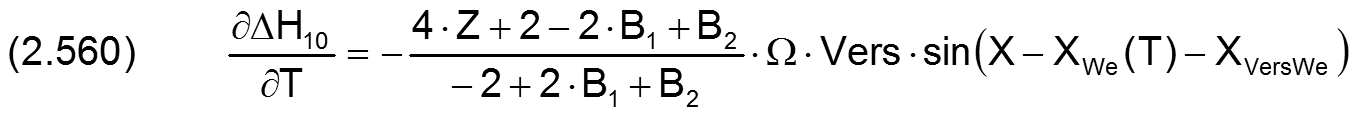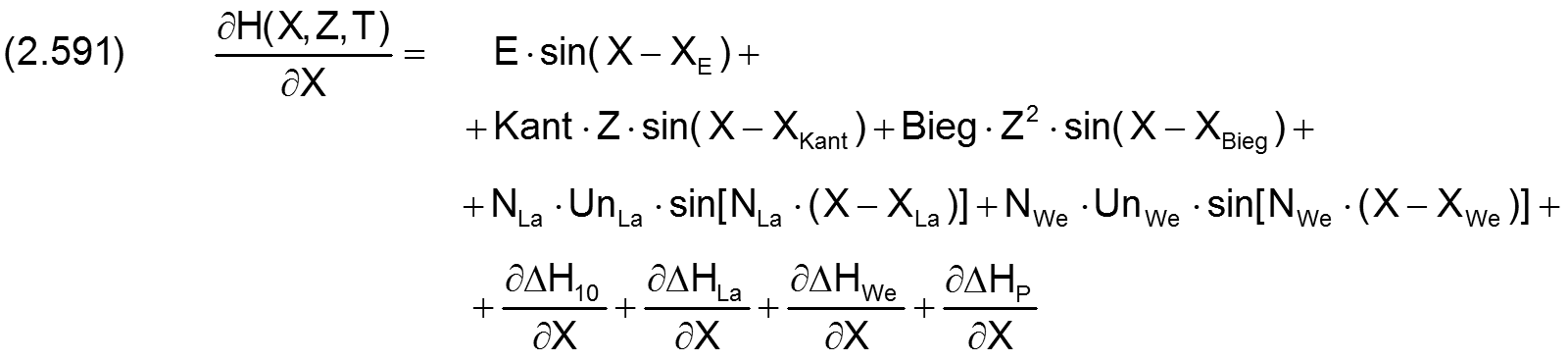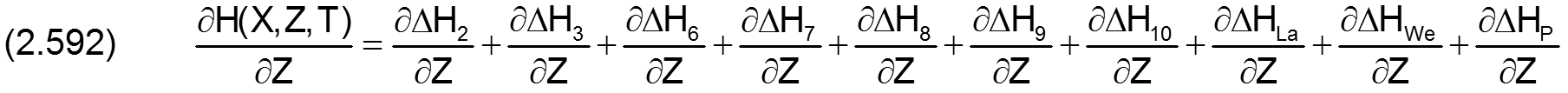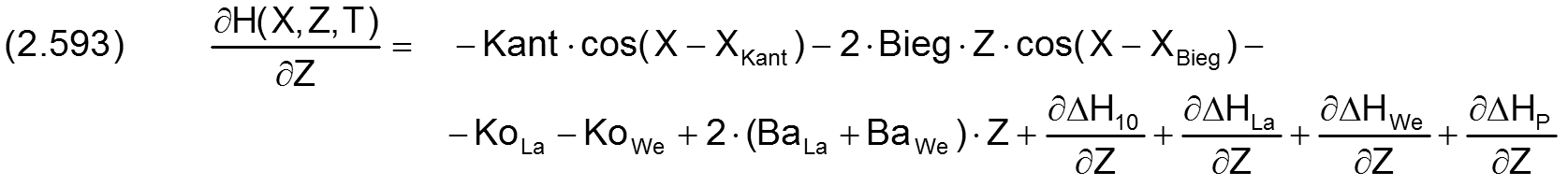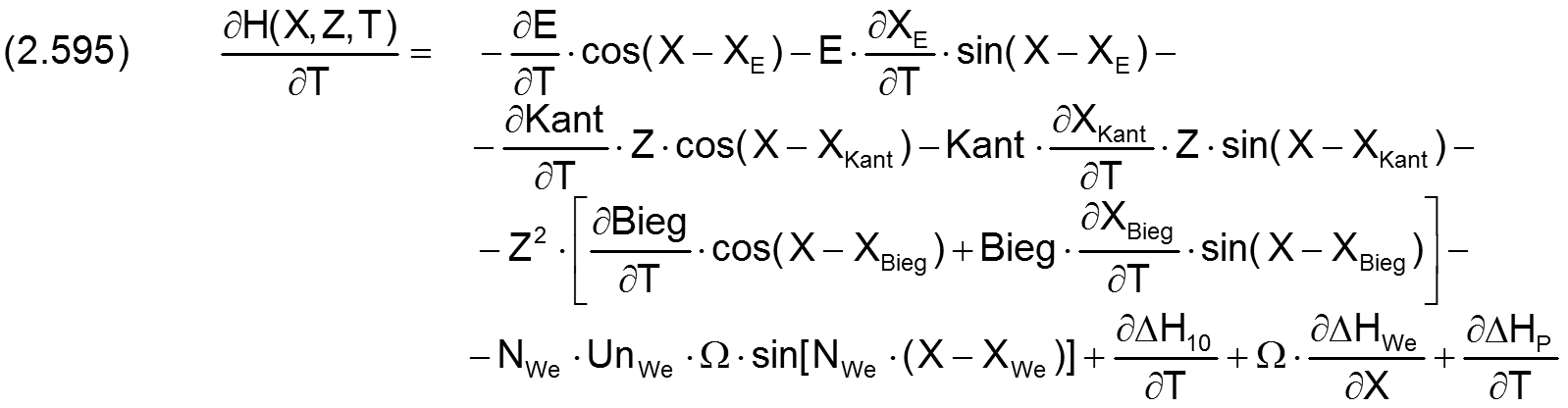zurück
weiter
zur dimensionsbehafteten Darstellung
2.2 Dimensionslose Darstellung des Lagers
In der hydrodynamischen Schmiertheorie hat es sich bewährt, mit dimensionslosen Größen zu arbeiten, basierend auf dem Ähnlichkeitsgesetz, das durch die Sommerfeldzahl gegeben ist.
Das Ähnlichkeitsgesetz besagt, dass geometrisch ähnliche Lager, die außerdem die gleiche Sommerfeldzahl aufweisen auch physikalisch ähnlich sind. So können Lager unterschiedlicher Größe, Drehzahl und Schmiermittelviskosität miteinander verglichen werden und Modellversuche für die Bewertung des Verhaltens eines größeren oder auch kleineren Originals herangezogen werden. Außerdem erübrigt sich nach der Berechnung eines konkreten Lagers die Berechnung aller anderen physikalisch ähnlichen Lager, da diese durch entsprechende Umrechnung aus den vorliegenden dimensionslosen Ergebnissen abgeleitet werden können.
Für den Wissenschaftler besteht der Vorteil darin, dass er generelle Untersuchungen anstellen kann, ohne sich zunächst um die konkreten Abmessungen eines bestimmten Lagers zu kümmern.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.1 Das dimensionslose Radiallager im Überblick
Die Grundlage zur Definition der dimensionslosen Parameter des Radialgleitlagers ist die Sommerfeldzahl So. Sie ist definiert durch
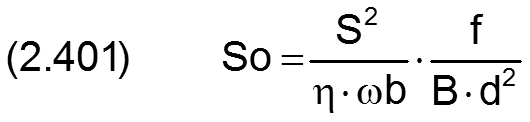
Die Sommerfeldzahl stellt die dimensionslos gemachte Lagerbelastung eines hydrodynamisch geschmierten Gleitlagers dar. Zur Umrechnung aller im Programm SIRIUS verwendeten dimensionsbehafteten in dimensionslose Parameter werden, wie für die Sommerfeldzahl, ausschließlich folgende 5 Bezugsparametern verwendet. Von diesen sind selbst nur 3 dimensionsbehaftet und zwei selbst bereits dimensionslos.
Verwendete Bezugsparameter:
| S |
relatives Lagerspiel (eigentlich bereits selbst dimensionslos; wird hier eingegeben und intern gespeichert in ‰) |
| B |
relative Lagerbreite (ist auch bereits dimensionslos) |
| d |
Nenndurchmesser des Lager (programmintern gespeichert in mm) |
| η |
dynamische Viskosität (programmintern gespeichert in mPa·s, Millipascal-Sekunden) |
| ωb |
Bezugswinkelgeschwindigkeit (programmintern gespeichert in rad/s) |
Das relative Lagerspiel S ist definiert durch

Die relative Lagerbreite B ist definiert durch

Nachfolgend wird für alle bereits eingeführten dimensionsbehafteten Parameter die Umrechnung in einen entsprechenden dimensionslosen Parameter angegeben, einschließlich der Gleichungen zu ihrer Berechnung in dimensionsloser Form.
Es gilt hier die Konvention: Die Bezeichnung der dimensionsbehafteten Parameter beginnt mit einem kleinen Buchstaben. Der entsprechende dimensionslose Parameter hat die gleiche Bezeichnung beginnend mit dem entsprechenden großen Buchstaben.
AUSNAHME: Die dimensionsbehaftete Lagerbelastung wird mit f bezeichnet und die dimensionslose mit So (Sommerfeldzahl). Das Symbol F steht für den Füllungsgrad, den es nur dimensionslos gibt.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.1.1 Koordinatensysteme im dimensionslosen Lager
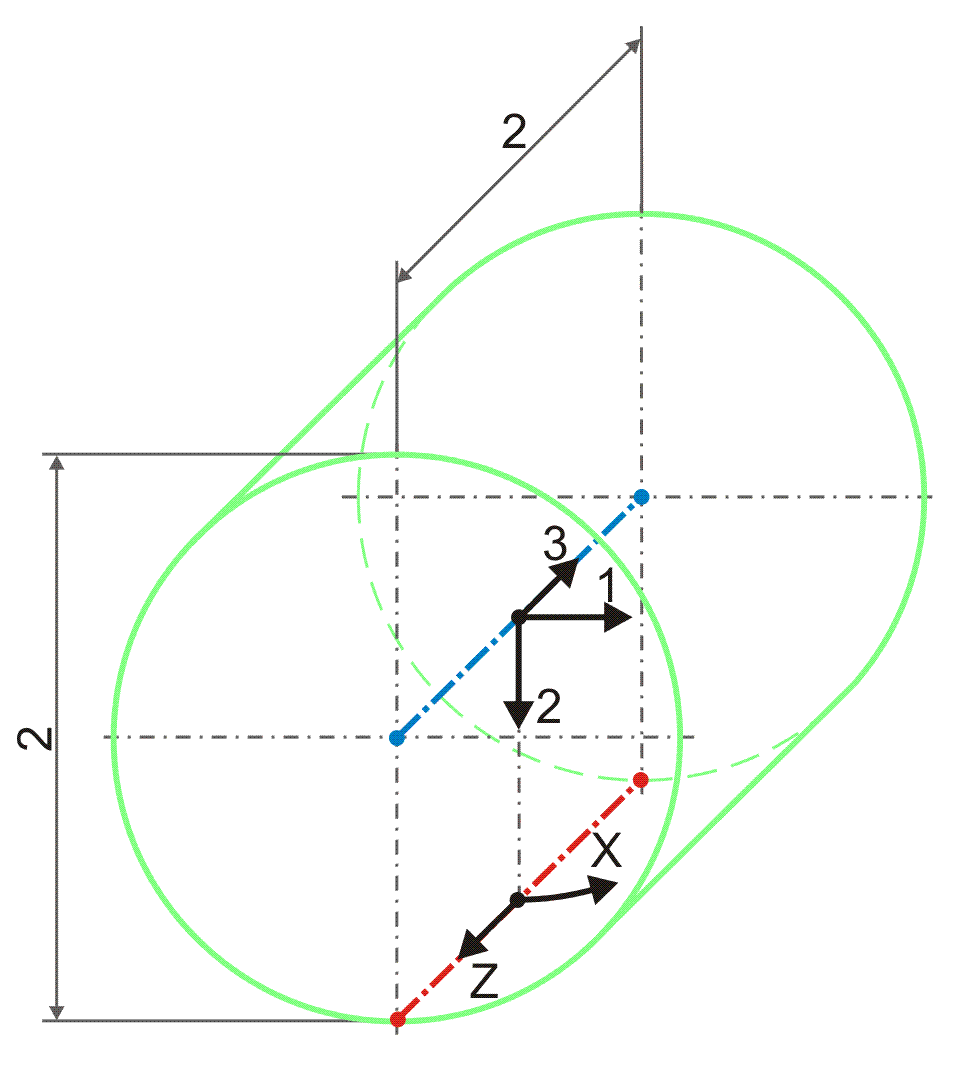
Bild 2.103 zeigt die Koordinatensysteme im dimensionslosen Lager. Eigentlich ist das dimensionslose Radialgleitlager grafisch nicht mehr widerspruchsfrei darstellbar, da der dimensionslose Umfang der voll umschlossenen Lagerschalengleitfläche 2·π beträgt, was einem Lagerschalenradius von eins entspricht und die mittlere dimensionslose Schmierspalthöhe ebenfalls eins beträgt. Deshalb wird in Bild 2.103 der dimensionslose Spalt nicht dargestellt.

Bild 2.103: Dimensionsloses lagerschalenfestes Koordinatensysteme in einem teilweise umschlossenen Lager
Die Ortskoordinaten des lagerschalenfesten Koordinatensystems x-y-z werden in folgender Weise dimensionslos gemacht
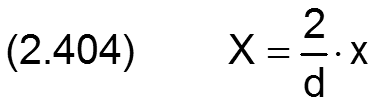 |
dimensionslose Umfangskoordinate |
HINWEIS:Die dimensionslose Umfangskoordinate X entspricht dem Winkel in Umfangsrichtung angegeben in Radiant. Deshalb werden im Text die meisten Winkel zur Angabe der Richtung eines Parameters durch ein großes X und die Bezeichnung des entsprechenden Parameters angegeben, z.B. die Richtung der dimensionslosen Lagerbelastung So wird bezeichnet mit X
So, oder die Richtung der Ebene der Verkantung Kant wird angegeben durch X
Kant.
Außerdem wird an der Programmoberfläche der kleine Buchstabe x in der Regel nicht als die dimensionsbehaftete Umfangskoordinate in mm verwendet, sondern nicht ganz korrekt zur Eingabe bzw. Anzeige eines entsprechenden Winkels in Grad, weil das in der Regel praktischer ist. Das ist leicht an der geforderten Maßeinheit "grd" zu erkennen, so dass Verwechslungen weitgehend ausgeschlossen sind.
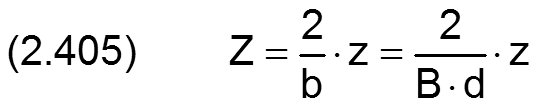 |
dimensionslose axiale Koordinate |
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.1.2 Darstellung des in die Ebene abgewickelten dimensionslosen Schmierspalts
Bild 2.104 zeigt das dimensionslose X-Z-Koordinatensystem im dimensionslosen abgewickelten Schmierspalt.
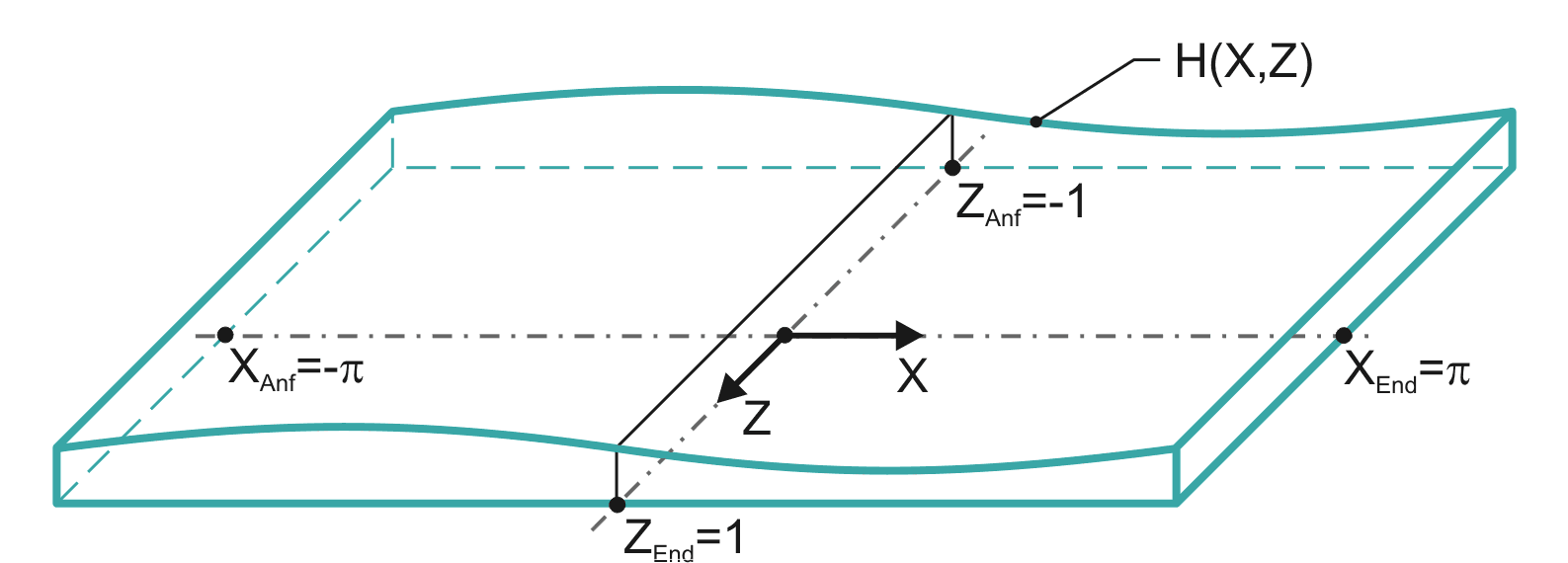
Bild 2.104: Abgewickelter dimensionsloser Schmierspalt H(X,Z) eines voll umschlossenen Lagers
Falls das Lager geometrisch und physikalisch symmetrisch ist, wird für die Berechnung nur der halbe Schmierspalt abgebildet gemäß Bild 2.105.
Bild 2.104 zeigt das dimensionslose X-Z-Koordinatensystem im dimensionslosen abgewickelten Schmierspalt.
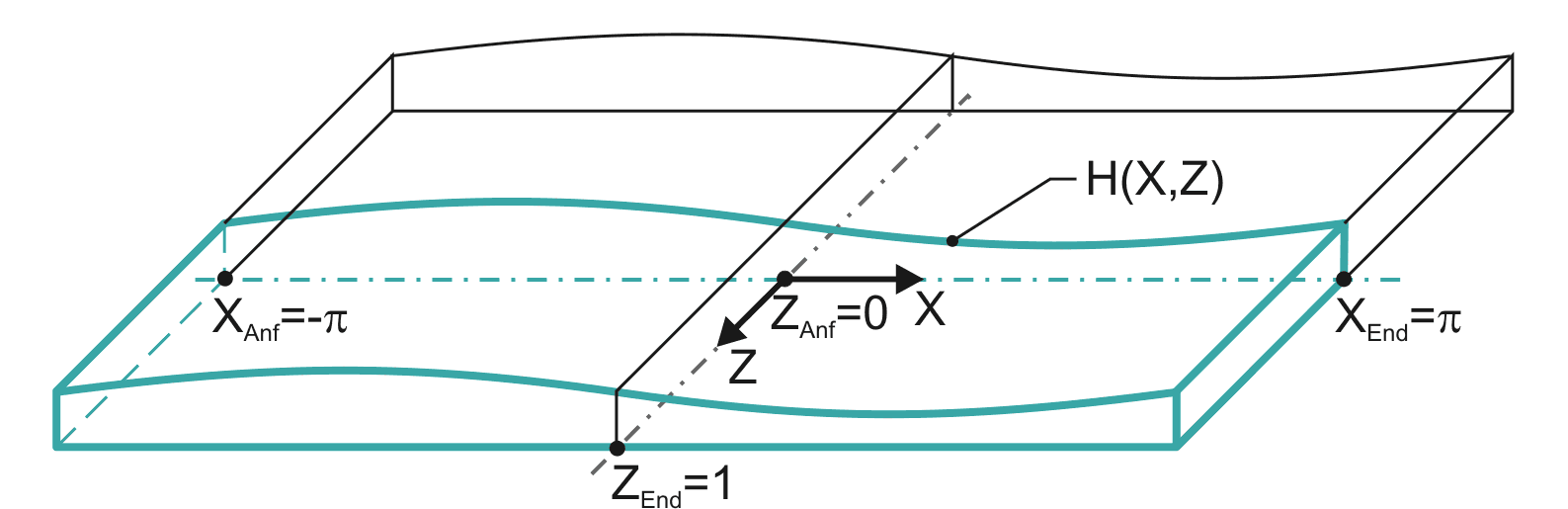
Bild 2.105: Abgewickelter dimensionsloser Schmierspalt H(X,Z) eines symmetrischen, voll umschlossenen Lagers (grüne Linie)
Die Anfangs- und Endkoordinaten des abgewickelten Schmierspalts in dimensionsloser Form ergeben sich nun aus den Gleichungen (2.006) bis (2.011) und (2.404),(2.405) mit


für das voll umschlossene Lager


für ein teilweise umschlossenes Lager
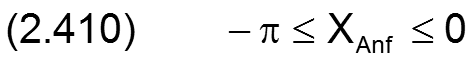
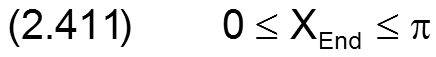
und
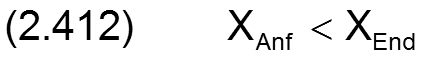
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.1.3 Dimensionsloser Spielraum der Welle in der Lagerschale
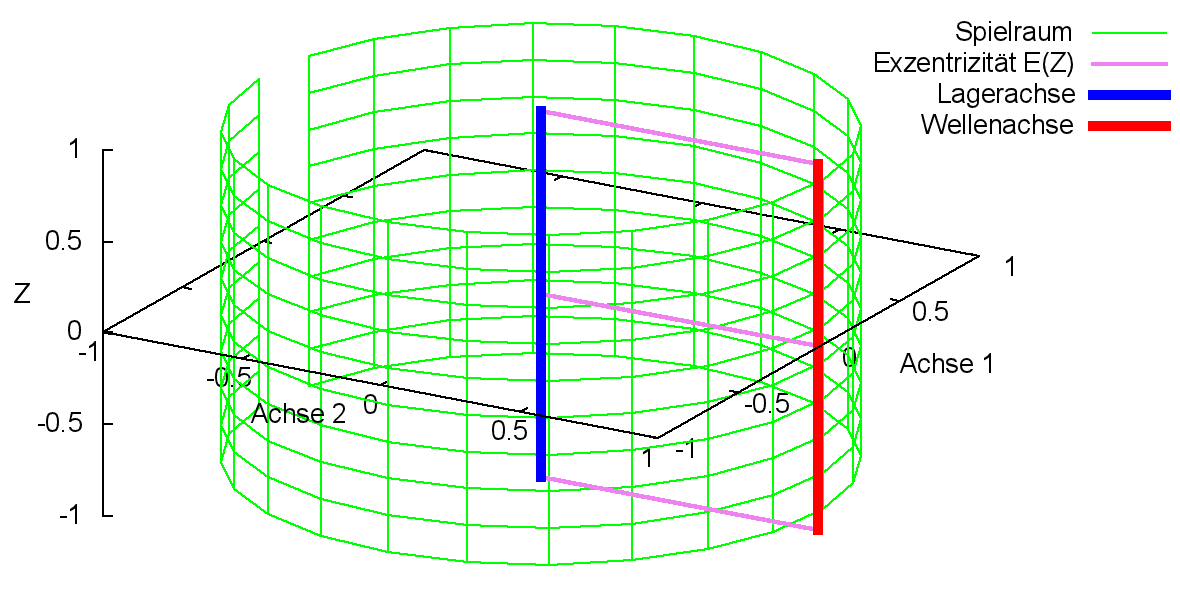
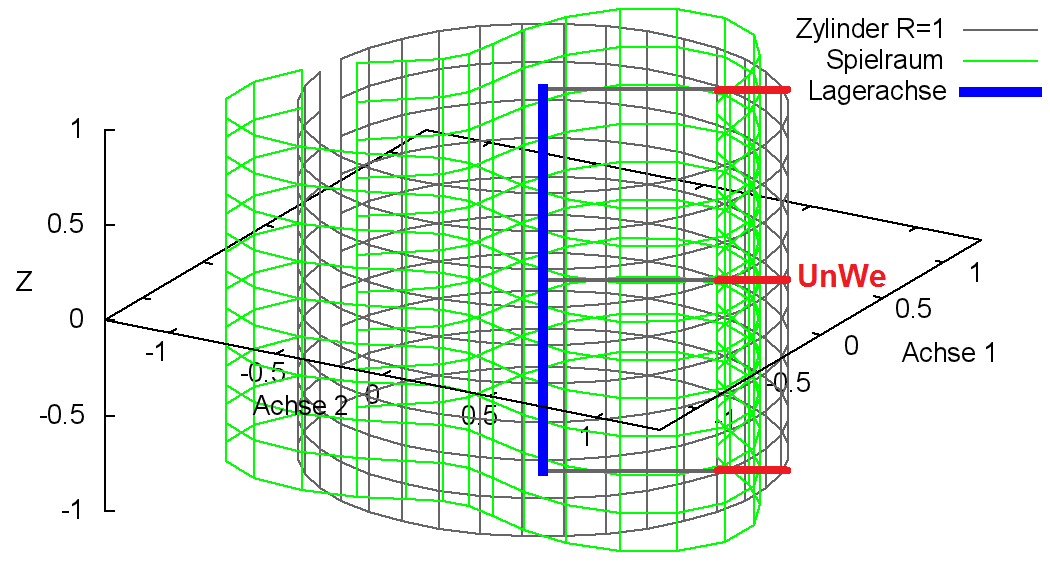
Analog zur dimensionslosen Spalthöhe H kann man den dimensionslosen Spielraum der Welle in der Lagerschale gemäß Bild 2.106 darstellen. Die dargestellte Lage der Welle entspricht hier wieder dem Zustand eines achsparallelen Lagers außer Betrieb, bei dem die Welle unten in der Lagerschale aufliegt.
Bild 2.106: Dimensionsloser Spielraum eines ideal zylindrischen Lagers; Prinzipskizze links und Darstellung mit SIRIUS/Gnuplot rechts
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.1.4 Die dimensionslose Wellendrehung
In der Literatur wird üblicher Weise die Drehgeschwindigkeit ω der Welle benutzt, um die Lagerbelastung f in die dimensionslose Sommerfeldzahl So umzuwandeln, so dass bei dimensionslosen Untersuchungen die Drehzahl nicht mehr explizit auftaucht. Das funktioniert so lange die Wellendrehzahl konstant ist. Da in SIRIUS auch instationäre Fälle mit sich kurzfristig ändernden Drehgeschwindigkeiten simuliert werden können, wird eine dimensionslose Drehgeschwindigkeit Ω eingeführt. Als Ersatz für die Wellendrehgeschwindigkeit in der Sommerfeldzahl wird eine zeitlich konstante Bezugswinkelgeschwindigkeit ωb eingeführt, die im Prinzip frei wählbar ist. Falls die Wellendrehgeschwindigkeit ω zeitlich konstant ist, ist es natürlich sinnvoll, die Bezugsdrehzahl ωb=ω zu wählen. Das entspricht dann der bisher üblichen Verfahrensweise. Wenn die Wellendrehzahl zeitlich variable ist, empfiehlt es sich für die Bezugswinkelgeschwindigkeit die mittlere oder die maximale Wellendrehgeschwindigkeit anzunehmen.
Die Winkelgeschwindigkeit der Welle wird in folgender Weise dimensionslos gemacht
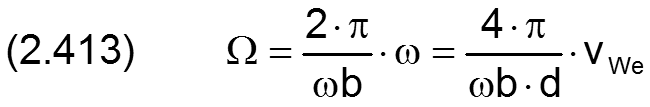
HINWEIS: Wenn die Wellendrehgeschwindigkeit ω=ωb ist, dann ist gemäß Definition die dimensionslose Wellendrehgeschwindigkeit Ω=2·π.
Im Programm SIRIUS können zeitlich konstante und variable Winkelgeschwindigkeiten angenommen werden. Durch die Eingabe eines Feldes von Winkelgeschwindigkeiten Ω(T) oder von Drehwinkeln XWe(T) der Welle für jeden zu berechnenden Zeitpunkt JT=1 bis NT können beliebige Geschwindigkeitsprofile abgebildet werden.
Um für grundsätzliche Untersuchungen die Modellierung einer Pendelbewegung mit der Eingabe weniger Parameter zu realisieren, wurde im Programm SIRIUS folgende Funktion zur Darstellung von Pendelbewegungen implementiert
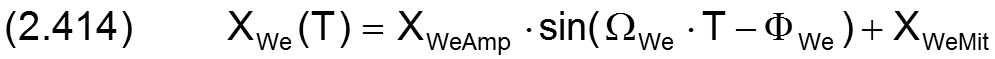
mit
| XWeAmp |
Amplitude des Wellendrehwinkels XWe |
| XWeMit |
Mittelwert des Wellendrehwinkels XWe |
| ΩWe |
Phasenwinkelgeschwindigkeit des Wellendrehwinkels XWe |
| ΦWe |
Phasenwinkel des Wellendrehwinkels XWe zum Zeitpunkt T=0 |
Die Phasenwinkelgeschwindigkeit ωWe und die Zeit t wurden dabei in folgender Weise dimensionslos gemacht
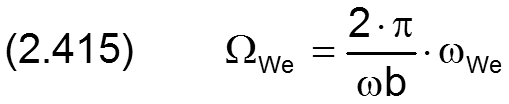
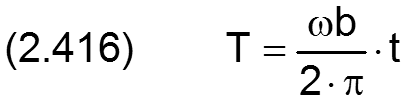
Die in den dimensionsbehafteten Gleichungen angegebenen Winkel sind bereits dimensionslos, sofern sie in Radiant angegeben sind, und brauchen deshalb nicht mehr dimensionslos gemacht werden.
Durch Differentiation der Gleichung (2.414) ergibt sich für die pendelnde Wellendrehung die Funktion der Winkelgeschwindigkeit Ω(T) mit
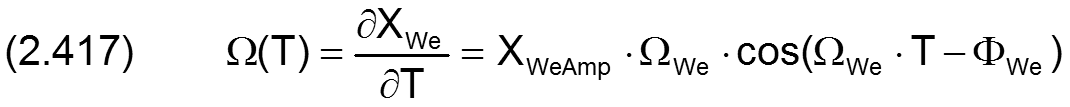
HINWEIS: Beachte den Unterschied zwischen der zeitlich variablen Wellendrehgeschwindigkeit Ω(T) und der zeitlich konstanten Phasenwinkelgeschwindigkeit ΩWe der Drehschwingung der Welle.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.1.5 Viskosität des Schmiermittels
Der Parameter der dynamischen Viskosität der Schmierflüssigkeit wird als Bezugsparameter ausschließlich dazu verwendet, andere Parameter dimensionslos zu machen, so dass eine dimensionslose dynamische Viskosität nicht benötigt wird und deshalb hier auch nicht definiert wird.
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2 Dimensionslose Schmierspaltgeometrie
Die Schmierspalthöhe h wird in folgender Weise dimensionslos gemacht
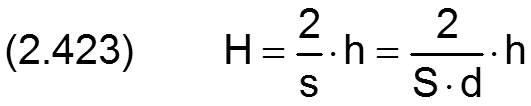
und die zugehörigen partiellen Ableitungen sind dann
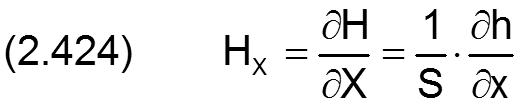

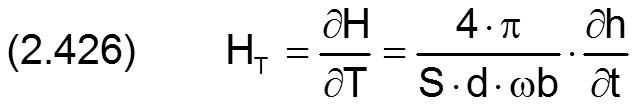
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.1 Dimensionsloser Ringspalt im ideal zylindrischen Lager mit konzentrischer Welle
Die dimensionslose Spalthöhe H0 des Ringspalts im konzentrischen ideal zylindrischen Lager ergibt sich aus (2.027) und (2.423) durch

und die partiellen Ableitungen sind alle Null

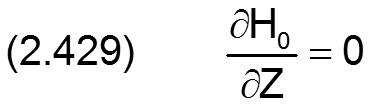
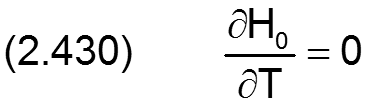
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.2 Dimensionslose achsparallele exzentrische Wellenverlagerung
Während der Verlagerungswinkel XE bereits als dimensionsloser Parameter angesehen werden kann (gemessen in Radiant) wird die Exzentrizität e in folgender Weise dimensionslos gemacht
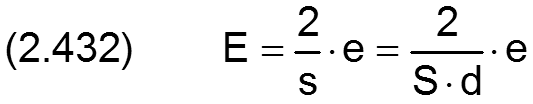
Die zugehörigen Ableitungen über die dimensionslose Zeit T sind
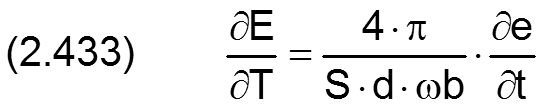
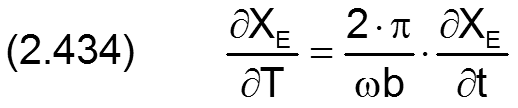
Die Änderung ΔH1 der dimensionslosen Spalthöhe H werden berechnet durch die Gleichungen
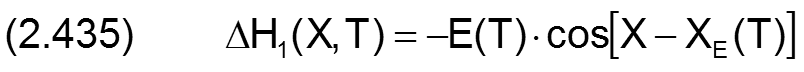
Die zugehörigen partiellen Ableitungen sind dann
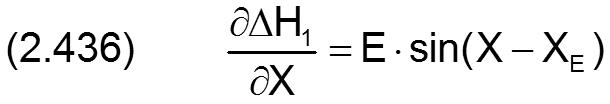
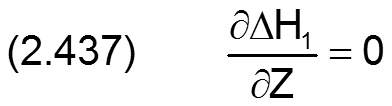
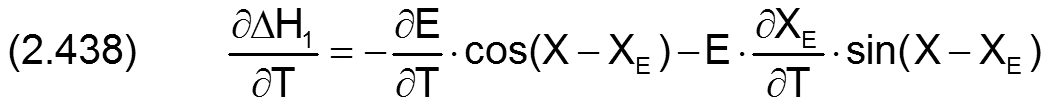
Statt durch den Betrag E und den Verlagerungswinkel XE ist die Exzentrizität auch bestimmt durch ihre Komponenten E1 und E2, wobei gilt
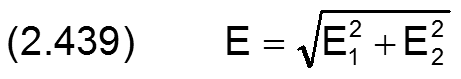

Die Änderung der Spalthöhe ΔH1 infolge der Exzentrizität kann auch durch die Komponenten E1 und E2 angegeben werden.
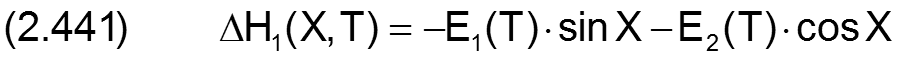
Die zugehörigen partiellen Ableitungen sind dann
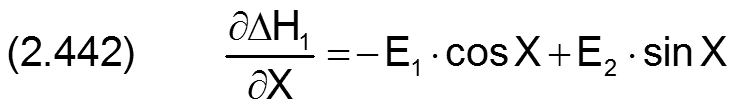

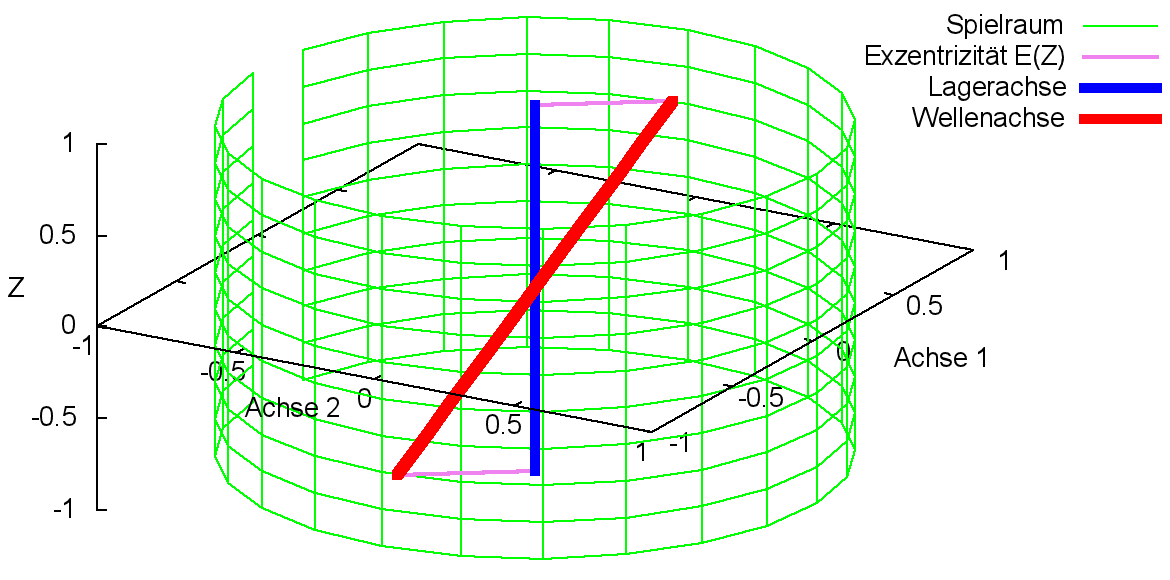
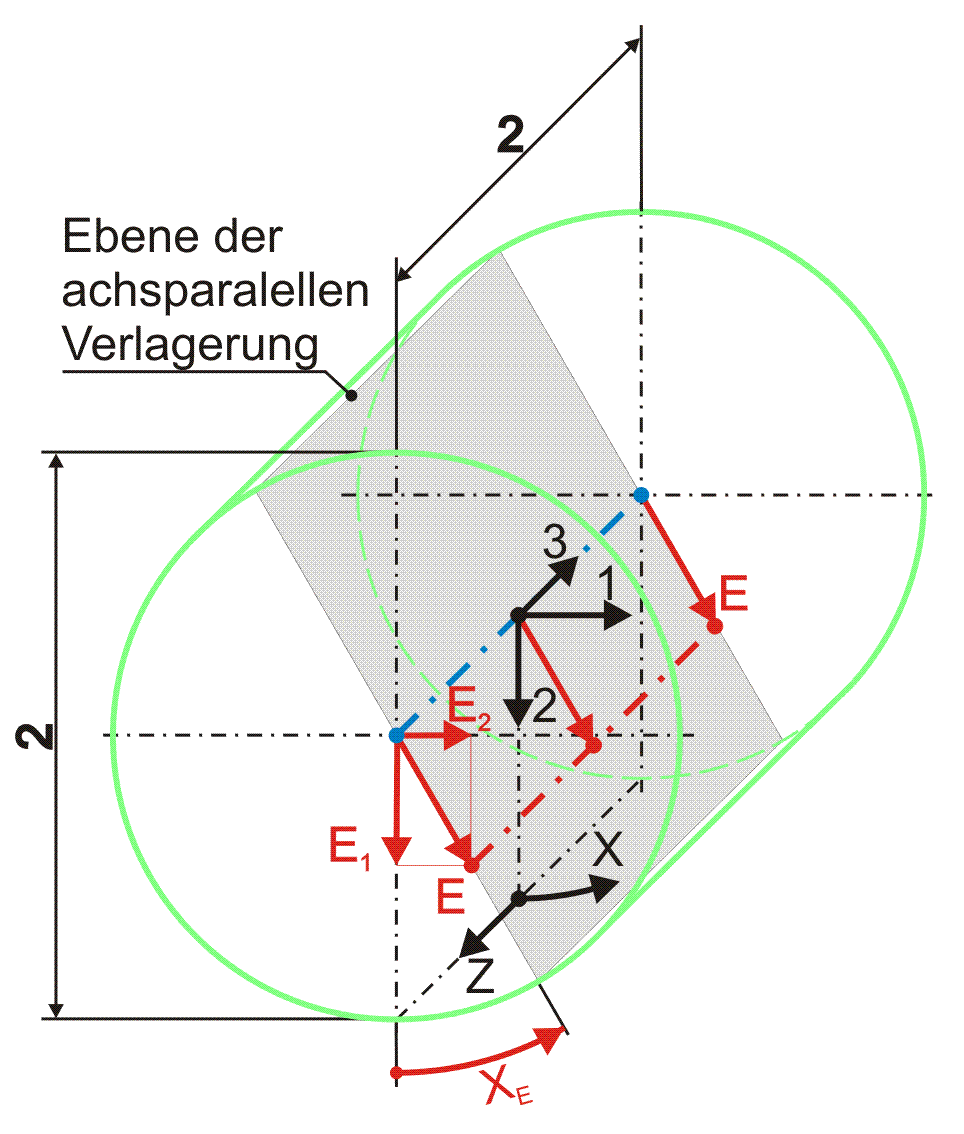
Bild 2.109 zeigt den dimensionslosen Spielraum (grün) eines ideal zylindrischen Lagers mit einer achsparallel verlagerten Wellenachse (rot).
 |
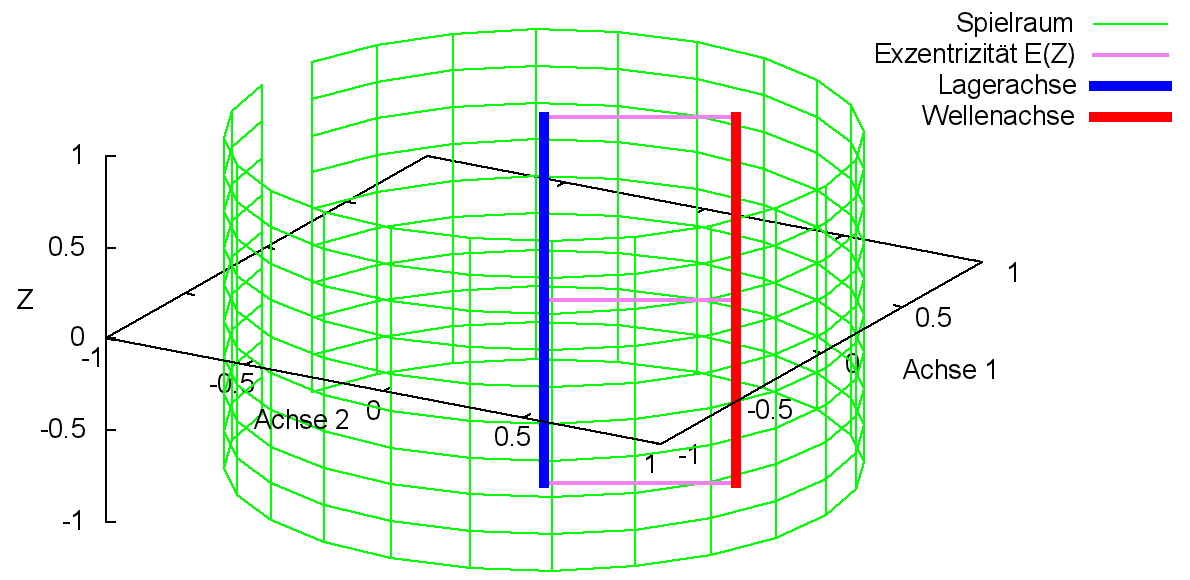 |
Bild 2.109: Dimensionslose achsparallele Verlagerung der Welle in der Lagerschale dargestellt im Spielraum des ideal zylindrischen Lagers; Prinzipskizze links und Darstellung mit SIRIUS/Gnuplot rechts
Im ideal zylindrischen Lager gilt für die dimensionslose Exzentrizität

zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.3 Dimensionslose Verlagerungsbahnen - instationäre Wellenverlagerungen
Die Verlagerung der Welle innerhalb der Lagerschale gegeben durch die Parameter der Exzentrizität E und den Verlagerungswinkel XE bzw. durch die Komponenten der Exzentrizität E1 und E2 können als konstant oder als zeitlich variabel angenommen werden. Wenn die Verlagerungsbahn aus einer vorgegebenen Lagerbelastung berechnet wird, werden die Parameter der Exzentrizität E(T) und XE(T) bzw. E1(T) und E2(T) punktweise für NT Zeitpunkte berechnet. Wenn die Lagerbelastung über die Zeit aus einer vorgegebenen (gemessenen) Verlagerungsbahn berechnet werden soll, dann können die entsprechenden Parameter der Exzentrizität ebenfalls für die zur berechnenden NT Zeitpunkte punktweise eingegeben werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lager, wenn noch keine konkreten Daten für die Verlagerungsbahn bekannt sind, können komplette Verlagerungsbahnen auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung von Verlagerungsbahnen implementiert.

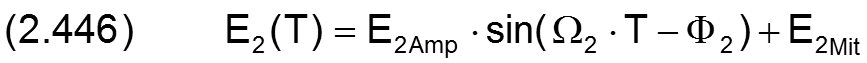
mit
| E1Amp |
Amplitude der Exzentrizität E1 |
| E1Mit |
Mittelwert der Exzentrizität E1 |
| Ω1 |
Phasenwinkelgeschwindigkeit der Exzentrizität E1 |
| Φ1 |
Phasenwinkel der Exzentrizität E1 zum Zeitpunkt T=0 |
| E2Amp |
Amplitude der Exzentrizität E2 |
| E2Mit |
Mittelwert der Exzentrizität E2 |
| Ω2 |
Phasenwinkelgeschwindigkeit der Exzentrizität E2 |
| Φ2 |
Phasenwinkel der Exzentrizität E2 zum Zeitpunkt T=0 |
Bild 2.110 zeigt ein Beispiel für eine dimensionslose Verlagerungsbahn mit den dimensionslosen Werten E1Amp = 0,2; E1Mit = 0; Ω1 = 2·π ; Φ1 = π/2; E2Amp = 0,5; E2Mit = 0,3; Ω2 = 2·π ; Φ2 = 0.

Bild 2.110: Beispiel für eine dimensionslose Verlagerungsbahn, die durch die Parameter einer Funktion vorgegeben wurde (Animation)
Für die Berechnung der partiellen Ableitung ∂H1/∂T der Spalthöhe über die Zeit werden auch die Ableitungen der Exzentrizitäten über die Zeit benötigt. Sie können exakt berechnet werden gemäß den Gleichungen (2.447) und (2.448) und müssen deshalb hier nicht näherungsweise ermittelt werden, wie für den Fall, wenn die Exzentrizitäten punktweise über die Zeit eingegeben werden.

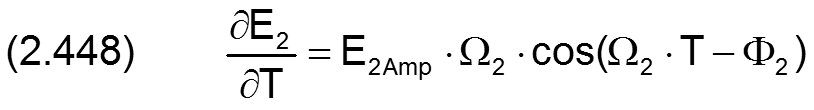
zurück
weiter
zur dimensionsbehafteten Darstellung
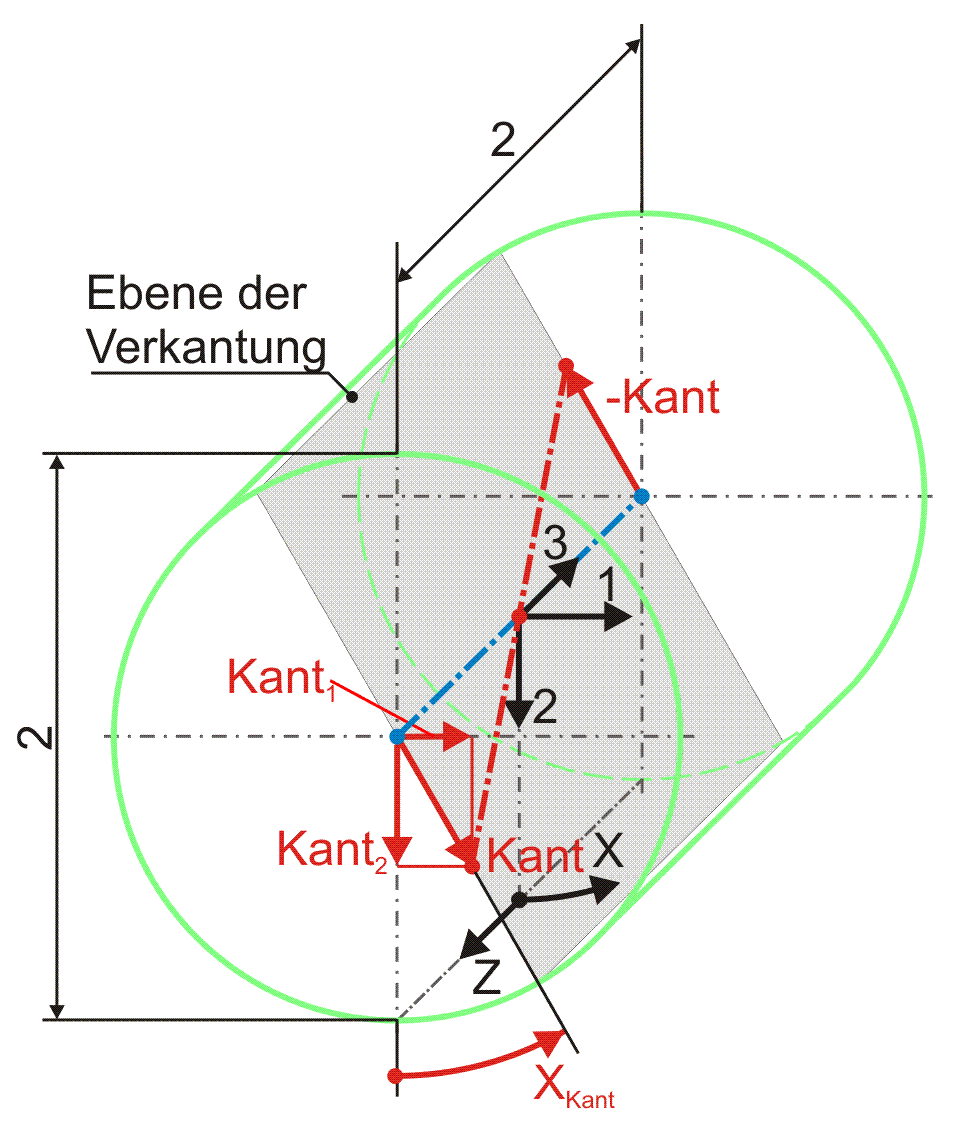
2.2.2.4 Dimensionslose Verkantung der Welle
Bild 2.112 zeigt den dimensionslosen Verlagerungsraum (grün) eines ideal zylindrischen Lagers mit einer verkanteten Wellenachse (rot).
Bild 2.112: Darstellung reiner Verkantung im dimensionslosen Spielraum; Prinzipskizze links und Darstellung mit SIRIUS/Gnuplot rechts
Der Betrag der Verkantung kant wird in folgender Weise dimensionslos gemacht
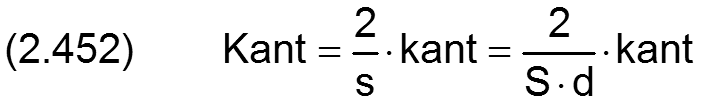
Im ideal zylindrischen Lager muss die dimensionslose Verkantung
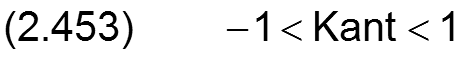
sein.
Die Ableitung nach der Zeit wird in folgender Weise dimensionslos gemacht
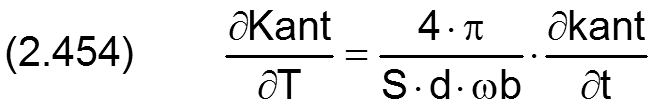
Die Ableitung des dimensionslosen Verkantungswinkels XKant über die dimensionslose Zeit T ist gegeben durch
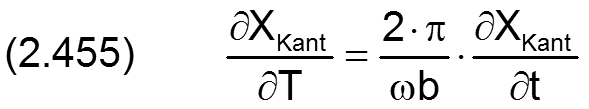
Die Änderung ΔH2 der dimensionslosen Spalthöhe H infolge Wellenverkantung wird berechnet durch
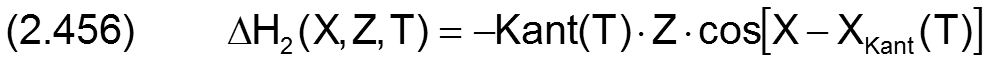
Die zugehörigen partiellen Ableitungen sind dann gegeben durch
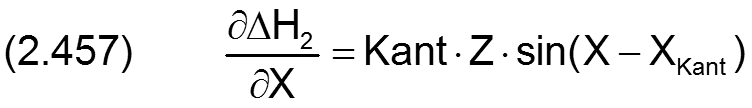
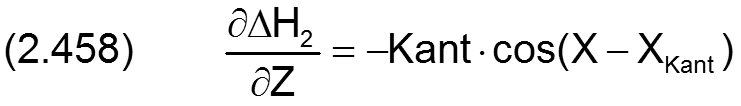
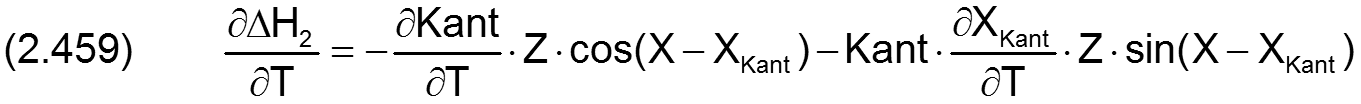
Statt durch den Betrag Kant und den Winkel XKant der Verkantungsebene ist die Verkantung auch bestimmt durch ihre Komponenten Kant1 und Kant2, wobei gilt
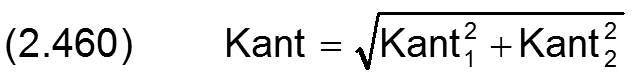

Die Änderung der Spalthöhe ΔH2 infolge der Verkantung kann auch durch die Komponenten Kant1 und Kant2 angegeben werden.
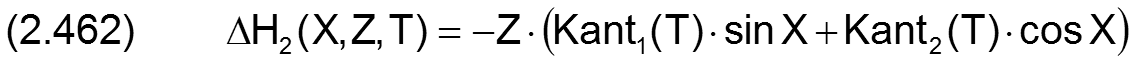
Die zugehörigen partiellen Ableitungen sind dann
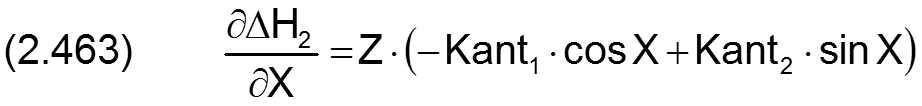
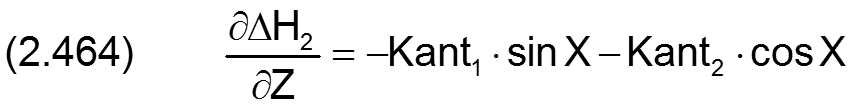
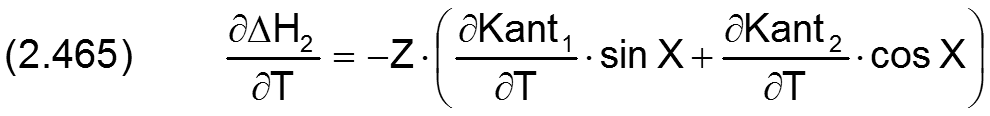
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.5 Variable dimensionslose Verkantung über die Zeit
Die Verkantung der Welle innerhalb der Lagerschale gegeben durch den Betrag Kant und den Winkel XKant der Verkantungsebene bzw. durch die Komponenten Kant1 und Kant2 können konstant sein oder als zeitlich variabel angenommen werden. Die Werte für die zeitabhängigen Werte der Verkantung können für alle NT Zeitpunkte der Berechnung punktweise eingegeben oder eingelesen werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lager, wenn noch keine konkreten Daten für die Verkantung bekannt sind, können komplette Verläufe der Verkantung auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung der Wellenverkantung implementiert.
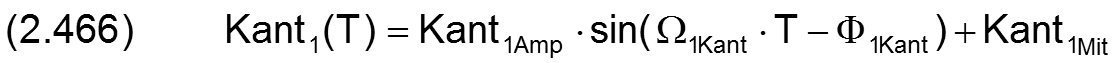
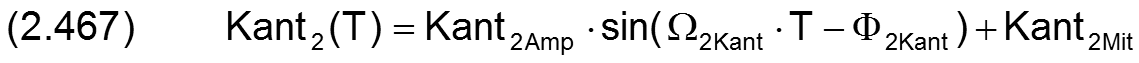
mit
| Kant1Amp |
Amplitude der Komponente Kant1 der Wellenverkantung |
| Kant1Mit |
Mittelwert der Komponente Kant1 der Wellenverkantung |
| Ω1Kant |
Phasenwinkelgeschwindigkeit der Komponente Kant1 der Verkantung |
| Φ1Kant |
Phasenwinkel der Komponente Kant1 der Verkantung zum Zeitpunkt T=0 |
| Kant2Amp |
Amplitude der Komponente Kant1 der Wellenverkantung |
| Kant2Mit |
Mittelwert der Komponente Kant2 der Wellenverkantung |
| Ω2Kant |
Phasenwinkelgeschwindigkeit der Komponente Kant2 der Verkantung |
| Φ2Kant |
Phasenwinkel der Komponente Kant2 der Verkantung zum Zeitpunkt T=0 |
Bild 2.114 zeigt ein Beispiel für eine Verlauf der Verkantung mit den dimensionslosen Werten Kant1Amp = 0,25; Kant1Mit = 0; Ω1Kant = 2·π; Φ1Kant = 0; Kant2Amp = 0,5; Kant2Mit = 0; Ω2Kant = π; Φ2Kant = 0.
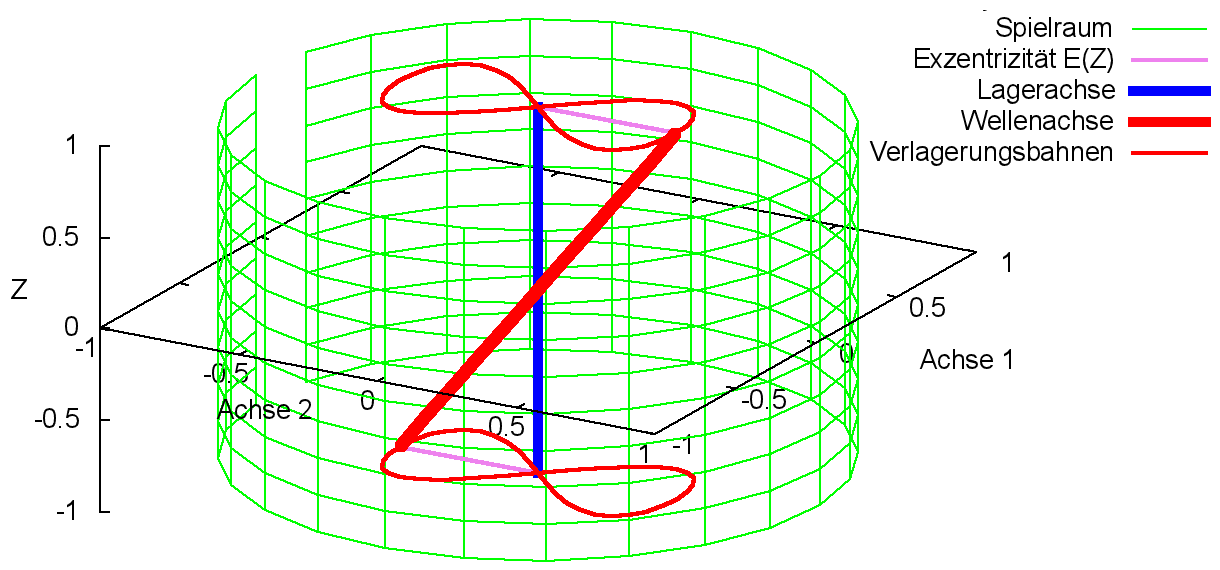
Bild 2.114: Beispiel für einen Verlauf der Verkantung, der durch die Parameter einer Funktion vorgegeben wurde (Animation)
Für die Berechnung der partiellen Ableitung ∂H2/∂T der Spalthöhe über die Zeit werden auch die Ableitungen der Verkantung über die Zeit benötigt. Sie können exakt berechnet werden gemäß den Gleichungen (2.468) und (2.469) und müssen deshalb hier nicht näherungsweise ermittelt werden, wie für den Fall, wenn die Verkantung punktweise über die Zeit eingegeben werden.
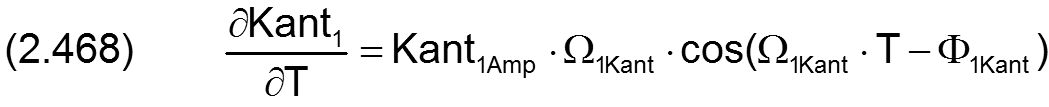
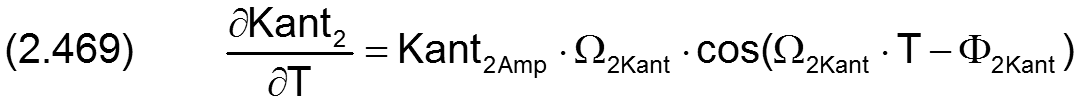
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.6 Dimensionslose punktweise gegebene Formabweichungen der Lagerschale und der Welle
Beliebige gemessene oder extern berechnete Formabweichungen der Lagerschale ΔHLa(X,Z) und/oder der Welle ΔHWe0(X,Z) können als Felder für jeden Gitterpunkt der abgewickelten Schmierspaltfläche in das Programm SIRIUS eingelesen werden.
Das Feld ΔHWe0(NZ,NX) beschreibt die punktweise angegebene Formabweichung der Wellengleitfläche bezogen auf eine angenommene ideale Zylinderfläche. Per Definition vergrößern positive Werte für ΔHWe0 die örtliche Spalthöhe. Außerdem sind die Werte dieses Feldes bezogen auf ein Gitternetz, welches mit der Wellenoberfläche fest verbunden ist und durch die Wellendrehung mitbewegt wird. Damit ergibt sich die Formabweichung ΔHWe(X,Z,T) der Welle bezogen auf das lagerschalenfeste Koordinatensystem X-Z durch die Beziehung
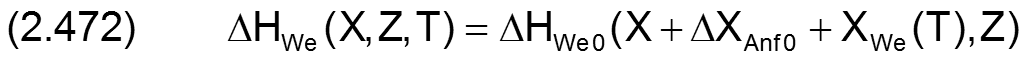
Dabei ist XWe(T) der dimensionslose Drehwinkel der Welle zum Zeitpunkt T und ΔXAnf0 der Versatz zwischen dem wellenfesten und dem Lagerschalenfesten Gitternetz, wenn der Drehwinkel der Welle XWe(T)=0 ist gemäß Bild 4.010.

Bild 4.010: Versatz der Gitternetze von Welle und Lagerschale
Die partiellen Ableitungen ∂ΔHWe/∂X und ∂ΔHWe/∂Z werden programmintern durch numerische Differentiation ebenfalls punktweise ermittelt. Die Formabweichung ΔHWe der Wellenoberfläche ist zeitlich konstant bezogen auf die Welle. Bezogen auf das lagerschalenfeste Koordinatensystem X-Z ist sie zeitlich variabel. Deshalb gilt für die partielle Ableitung über die Zeit bezogen auf das lagerschalenfeste Koordinatensystem X-Z.
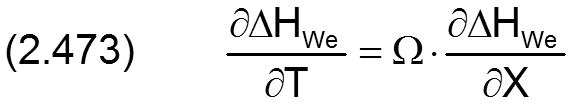
Das Feld ΔHLa(NZ,NX) beschreibt die punktweise angegebene Formabweichung der Lagerschalengleitfläche bezogen auf eine angenommene ideale Zylinderfläche. Per Definition vergrößern positive Werte für ΔHLa die örtliche Spalthöhe. Die partiellen Ableitungen ∂ΔHLa/∂X und ∂ΔHLa/∂Z der Formabweichungen der Lagerschale werden programmintern durch numerische Differentiation ebenfalls punktweise ermittelt. Die Formabweichung ΔHLa der Lagerschale ist zeitlich konstant, deshalb gilt bezogen auf das Lagerschalenfeste Koordinatensystem X-Z
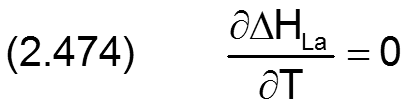
HINWEIS: Mit dem Feld ΔHLa(N
Z,N
X) können auch extern berechnete zeitlich konstante elastische Formabweichungen der Lagerschale berücksichtigt werden. Elastische Formabweichungen die programmintern über eine dimensionslose Elastizitätsmatrix Chp berechnet werden sollen und so auch instationäre Verformungen erfassen können, werden nicht durch ΔH
La(N
Z,N
X) erfasst. Siehe dazu Abschnitt
2.2.2.17.
Da die Ermittlung und Eingabe punktweise gegebener Formabweichungen recht aufwendig ist, sind für prinzipielle Untersuchungen des Einflusses von Formabweichungen im Programm SIRIUS einige durch Funktionen modelliert, so dass ihre Eingabe einfach durch wenige Parameter realisiert werden kann. Nachfolgend sind die verfügbaren Formabweichungen und die zugehörigen Funktionen angegeben
zurück
weiter
zur dimensionsbehafteten Darstellung
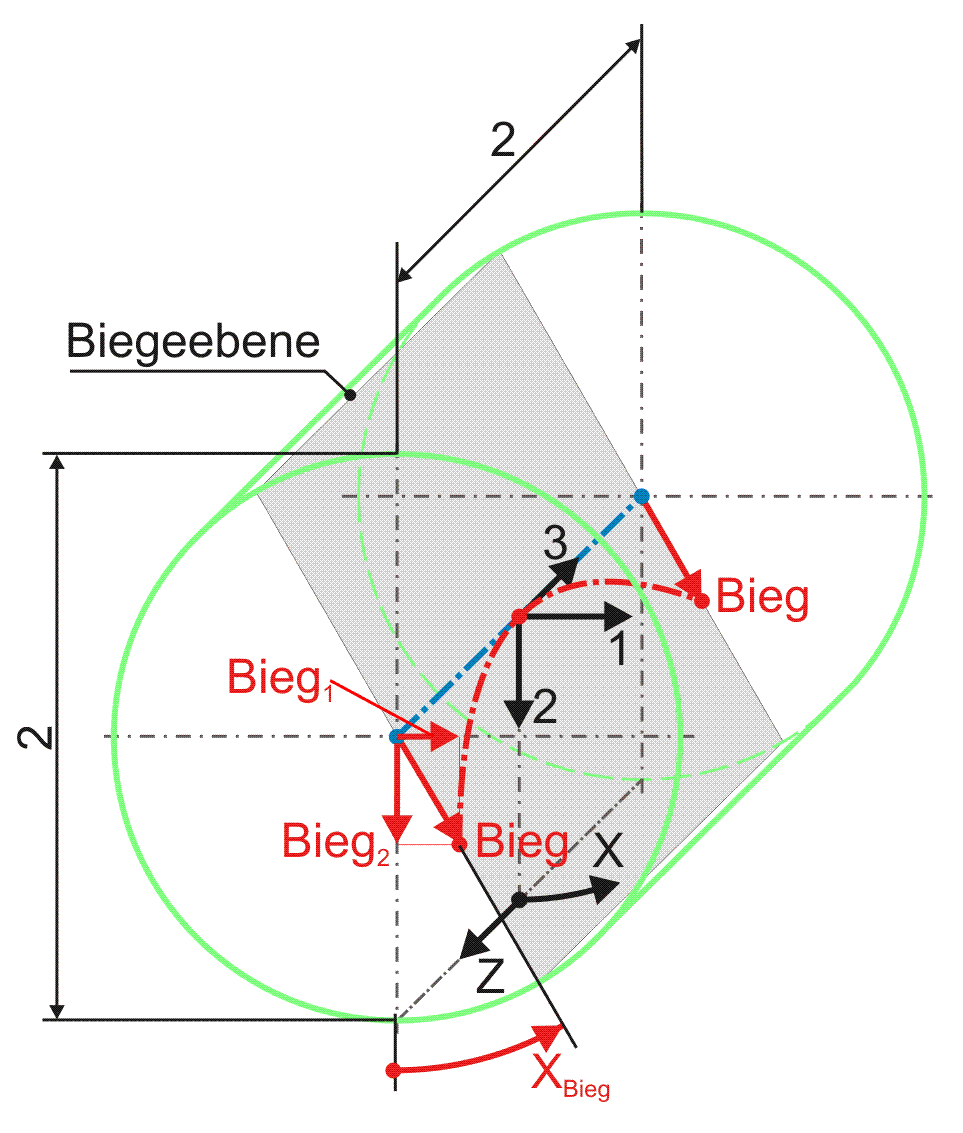
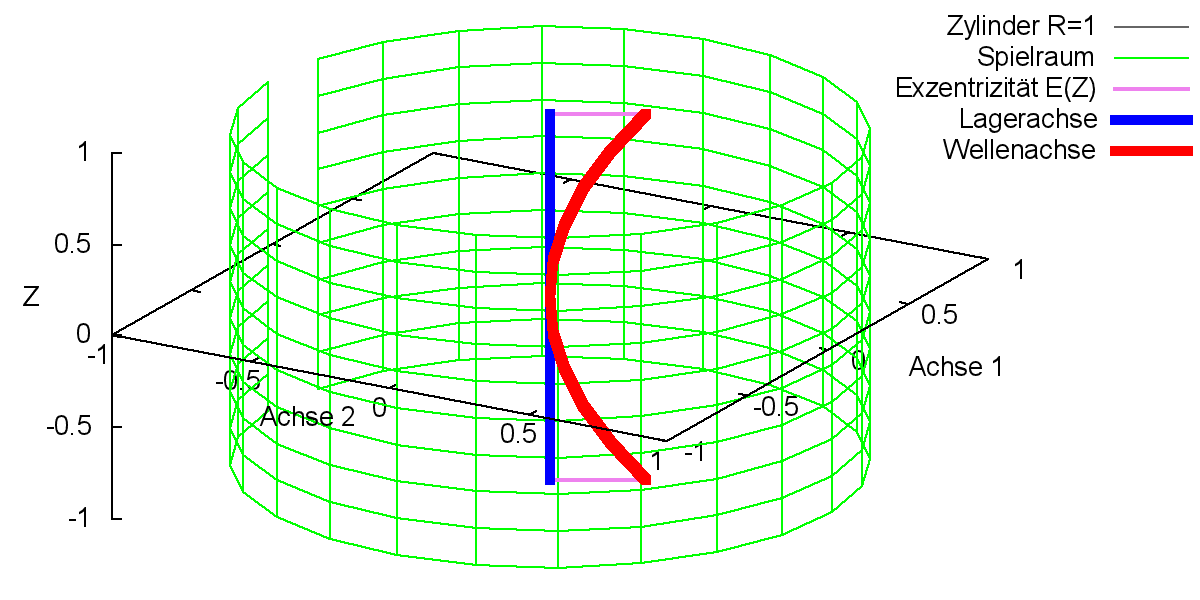
2.2.2.7 Dimensionslose gebogene Welle
Bild 2.116 zeigt den dimensionslosen Spielraum (grün) eines ideal zylindrischen Lagers mit einer gebogenen Wellenachse (rot).
Bild 2.116: Reine Wellenbiegung dargestellt im dimensionslosen Spielraum des ansonsten ideal zylindrischen Lagers; Prinzipskizze links und Darstellung mit SIRIUS/Gnuplot rechts
Bei reiner Biegung muss diese kleiner sein als eins. Bei Überlagerung mit einer entgegen gerichteten achsparallelen Verlagerung könnte die Biegung theoretisch aber auch einen Wert annehmen, der bis knapp an 2 reicht , was aber unrealistisch ist, weil dann kaum noch eine hydrodynamische Tragfähigkeit des Lagers gegeben ist.

Bei einem positiven Wert für Bieg zeigt der Vektor der Biegung in Richtung des Schenkels des Winkels XBieg gemäß Bild 2.116.
Der Betrag der Wellenbiegung bieg und dessen Ableitung nach der Zeit t werden in folgender Weise dimensionslos gemacht
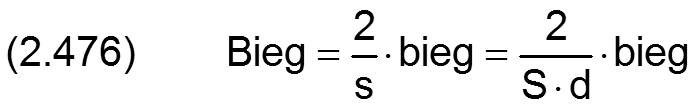
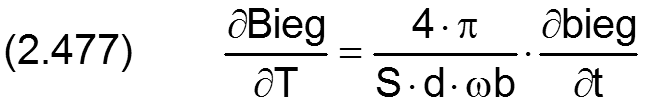
Die Ableitung des bereits dimensionslosen Winkels XBieg der Lage der Biegeebene über die Zeit ist definiert durch
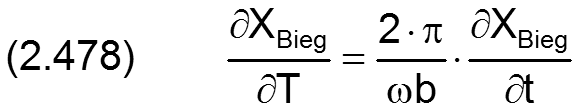
Die Änderung ΔH3 der dimensionslosen Spalthöhe infolge Wellenbiegung wird berechnet durch

Die zugehörigen partiellen Ableitungen sind dann gegeben durch
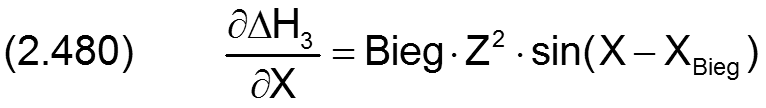
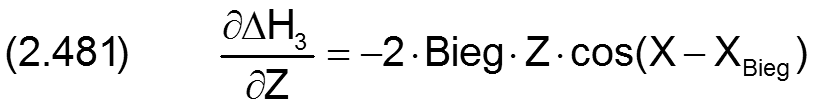

Statt durch den Betrag Bieg und den Winkel XBieg der Biegeebene ist die Biegung auch bestimmt durch ihre Komponenten Bieg1 und Bieg2, wobei gilt


Die Änderung der dimensionslosen Spalthöhe ΔH3 infolge der Biegung kann auch durch die Komponenten Bieg1 und Bieg2 angegeben werden.
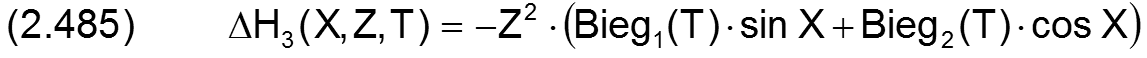
Die zugehörigen partiellen Ableitungen sind dann
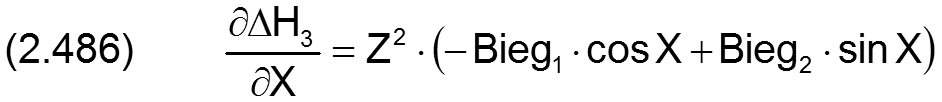
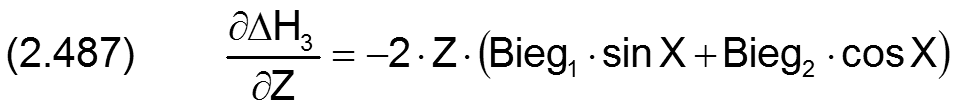
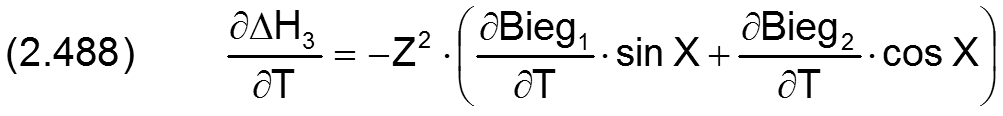
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.8 Variable dimensionslose Wellenbiegung über die Zeit
Die Biegung der Welle innerhalb der Lagerschale gegeben durch den Betrag Bieg und den Winkel XBieg der Biegeebene bzw. durch die Komponenten Bieg1 und Bieg2 können konstant sein oder als zeitlich variabel angenommen werden. Die Werte für die zeitabhängigen Werte der Biegung können für alle NT Zeitpunkte der Berechnung punktweise eingegeben oder eingelesen werden.
Für prinzipielle Untersuchungen des dynamischen Verhaltens des Lager, wenn noch keine konkreten Daten für die Biegung bekannt sind, können komplette Verläufe der Biegung auch durch zyklische Funktionen mit einigen wenigen Parametern eingegeben werden, wodurch sich die Dateneingabe wesentlich vereinfacht. Dafür sind in SIRIUS folgende Funktionen zur Darstellung von Wellenbiegung implementiert.
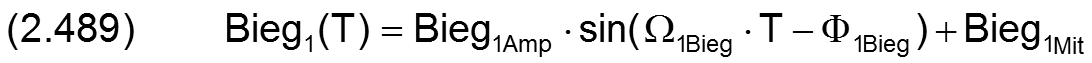
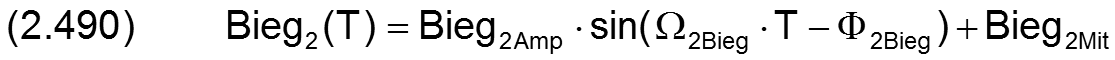
mit
| Bieg1Amp |
Amplitude der Komponente Bieg1 der Wellenbiegung |
| Bieg1Mit |
Mittelwert der Komponente Bieg1 der Wellenbiegung |
| Ω1Bieg |
Phasenwinkelgeschwindigkeit der Komponente Bieg1 der Biegung |
| Φ1Bieg |
Phasenwinkel der Komponente Bieg1 der Biegung zum Zeitpunkt T=0 |
| Bieg2Amp |
Amplitude der Komponente Bieg2 der Wellenbiegung
|
| Bieg2Mit |
Mittelwert der Komponente Bieg2 der Wellenbiegung |
| Ω2Bieg |
Phasenwinkelgeschwindigkeit der Komponente Bieg2 der Biegung |
| Φ2Bieg |
Phasenwinkel der Komponente Bieg2 der Biegung zum Zeitpunkt T=0 |
Bild 2.117 zeigt ein Beispiel für einen Verlauf der Biegung mit den Werten Bieg1Amp = 0,5; Bieg1Mit = 0; Ω1Bieg = 2·π; Φ1Bieg = 0; Bieg2Amp = 0,5; Bieg2Mit = 0; Ω2Bieg = 2·π; Φ2Bieg = -π/2.
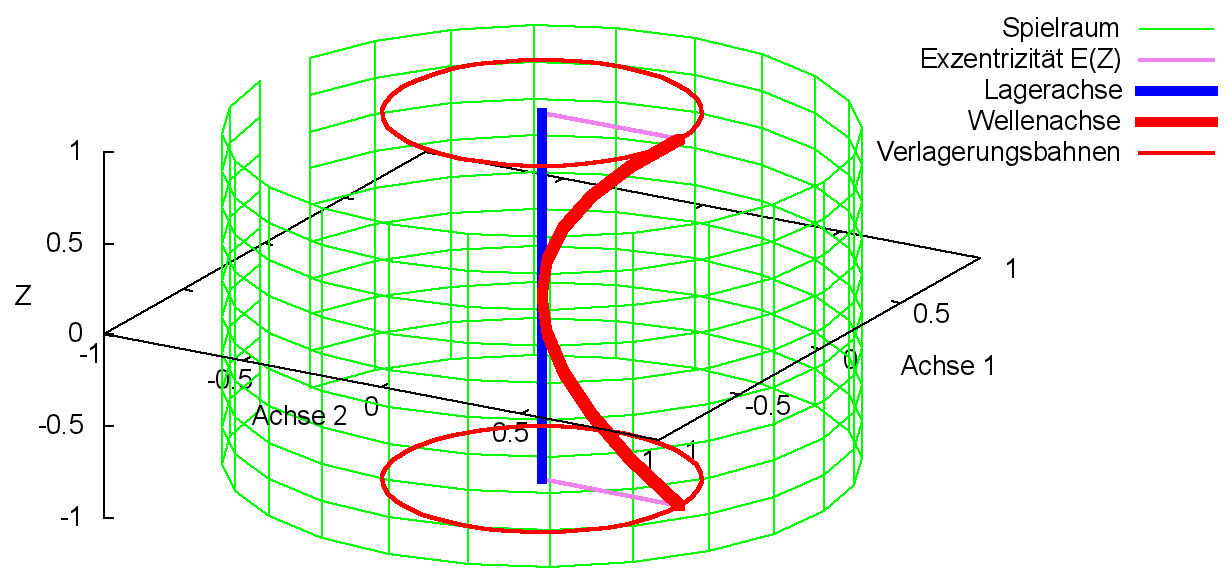
Bild 2.117: Beispiel für einen Verlauf der Biegung, der durch die Parameter einer Funktion vorgegeben wurde (Animation)
Für die Berechnung der partiellen Ableitung ∂ΔH3/∂T der Spalthöhe über die Zeit werden auch die Ableitungen der Wellenbiegung über die Zeit benötigt. Sie können exakt berechnet werden gemäß den Gleichungen (2.491) und (2.492) und brauchen deshalb hier nicht näherungsweise ermittelt werden wie für den Fall, wenn die Biegung punktweise über die Zeit eingegeben wird.

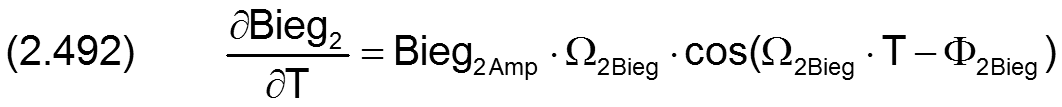
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.9 Dimensionslose Formabweichung der Lagerschale über den Umfang
Bild 2.119 zeigt den dimensionslosen Spielraum (grün) eines Lagers mit leicht elliptischer Lagerschale und ideal zylindrischer Welle in einer grafischen Darstellung durch SIRIUS/Gnuplot. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
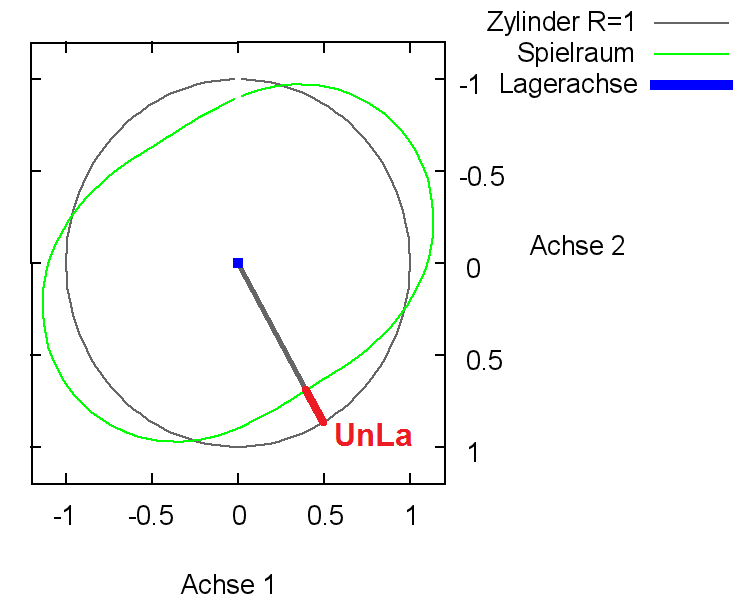
Bild 2.119: Dimensionsloser Spielraum eines Lagers mit elliptischer Lagerschale und ideal zylindrischer Welle
Verkleinert das Maximum an der Stelle XLa die Spalthöhe wird UnLa als positiver Wert angegeben, vergrößert das Maximum die Spalthöhe als negativer Wert.
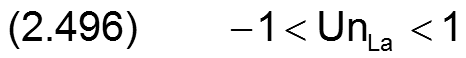
NLa ist die Anzahl der Unrundheitszyklen über den Umfang. Für eine elliptische Lagerschale ist NLa=2 und für alle anderen eine natürliche Zahl größer 2.

Der Betrag der Unrundheit der Lagerschale wird in folgender Weise dimensionslos gemacht

Die Änderung ΔH4 der dimensionslosen Spalthöhe H infolge Unrundheit der Lagerschale wird berechnet durch
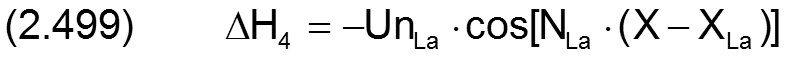
Die zugehörigen partiellen Ableitungen sind dann gegeben durch
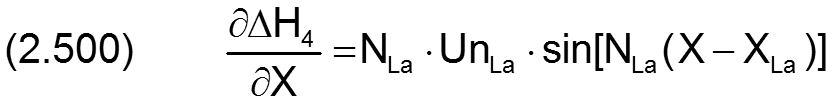
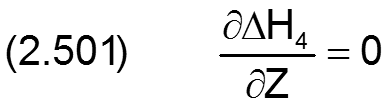
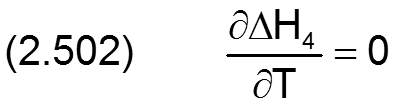
zurück
weiter
zur dimensionsbehafteten Darstellung
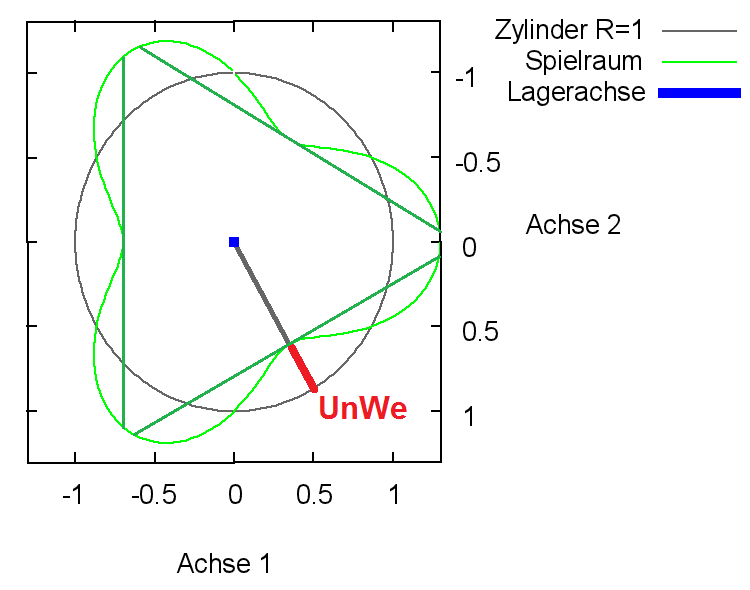
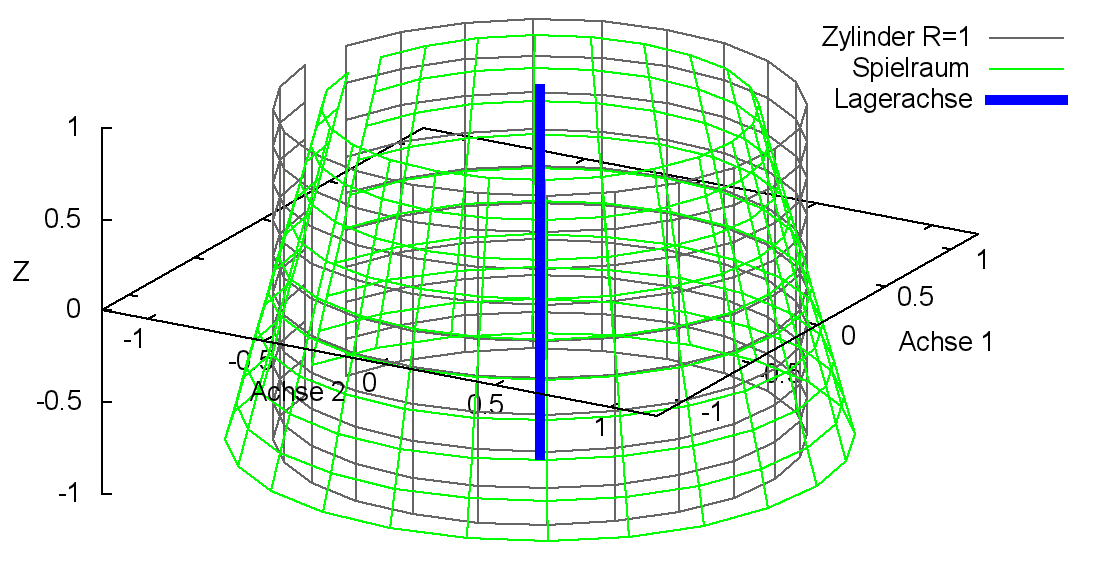
2.2.2.10 Dimensionslose Formabweichung der Welle über den Umfang
Bild 2.121 zeigt den dimensionslosen Spielraum (grün) eines Lagers mit "dreieckiger" Welle und ideal zylindrischer Lagerschale in einer grafischen Darstellung durch SIRIUS/Gnuplot. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
Bild 2.121: Dimensionsloser Spielraum eines Lagers mit "dreieckiger" Welle und ideal zylindrischer Lagerschale
Verkleinert das Maximum an der Stelle XWe(T) die Spalthöhe wird UnWe als positiver Wert angegeben, vergrößert das Maximum die Spalthöhe als negativer Wert.
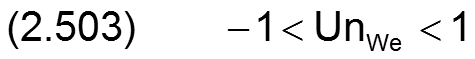
NWe ist die Anzahl der Unrundheitszyklen über den Umfang. Für eine "dreieckige" Welle ist NWe=3.

HINWEIS:Der Spielraum, der mit SIRIUS/Gnuplot grafisch dargestellt wird, entspricht nur so lange dem tatsächlichen Spielraum, solange der Querschnitt durch die Mantelfläche eine konvexe Geometrie aufweist. Falls dieser Querschnitt wie im gezeigten Beispiel des Bildes 2.121 konkav ist, verkleinert sich der tatsächliche Spielraum, in dem sich die Wellenachse bewegen kann, wie er in Bild 2.121 rechts durch die eingezeichneten grünen Geraden weiter eingeschränkt wird. Physikalisch bedeutet das, dass im Schmierspalt mehrere Stellen mit lokalen minimalen Schmierspalthöhen entstehen und so mehrere hydrodynamische Druckberge entstehen können, wie im Bild
2.123 gezeigt wird. Damit entsteht praktisch ein Mehrgleitflächenlager. Das gilt nicht nur für Unrundheit der Welle sondern auch für die Unrundheit der Lagerschale und deren Überlagerungen.
Weiterhin ist zu beachten, dass sich der verformte Spielraum mit der Welle mitdreht.
Der Betrag der Unrundheit unWe der Welle und die Winkelgeschwindigkeit der Welle ω=∂XWe/∂t werden in folgender Weise dimensionslos gemacht
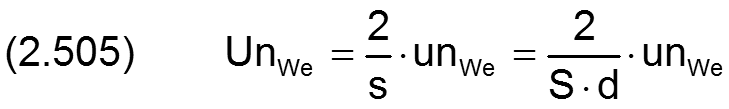
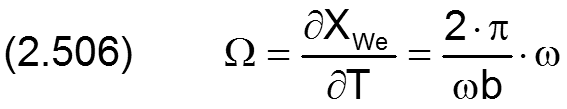
Die Änderung ΔH5 der dimensionslosen Spalthöhe infolge Unrundheit der Welle wird berechnet durch

Die zugehörigen partiellen Ableitungen sind dann gegeben durch
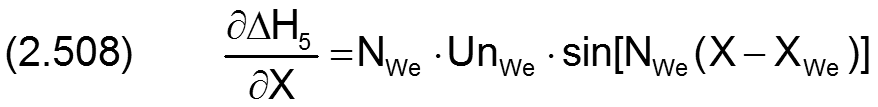
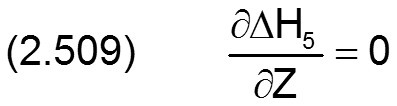
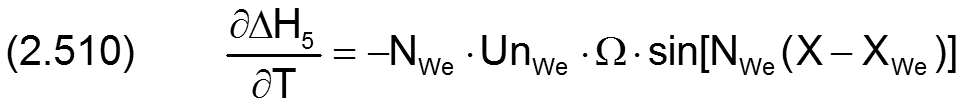
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.11 Überlagerung von dimensionslosen Unrundheiten der Lagerschale und der Welle
Bereits bei der Überlagerung einer Unrundheit der Lagerschale und einer Unrundheit der Welle ist die Gestalt des Spielraums nicht mehr so einfach zu überschauen, denn dieser ändert mit der Drehung sowohl seine Lage als auch seine Form. Bild 2.122 zeigt als Beispiel den Spielraum (grün) in axialer Ansicht für eine "dreieckige" Welle (UnWe=0,4; NWe=3), die in einer elliptischen Lagerschale läuft (UnLa=0,3; NLa=2) zu irgend einem Zeitpunkt und in der Animation (nur HTML-Version) seine Veränderung über eine Umdrehung der Welle.
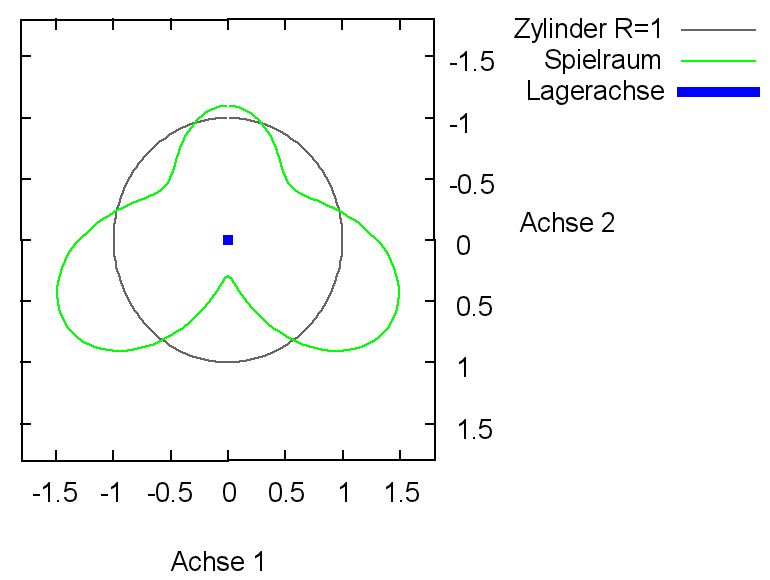
Bild 2.122: Axiale Ansicht des dimensionslosen Spielraums eines Lagers mit elliptischer Lagerschale und "dreieckiger" Welle in konzentrischer Lage (Animation)
In diesem Beispiel wird angenommen, dass die Welle konzentrisch in der Lagerschale läuft. Trotzdem entwickelt sich hierbei im Schmierspalt bereits ein instationärer Druckverlauf P(T) mit mehreren Druckbergen, wie in Bild 2.123 für den in Bild 2.122 gewählten Zeitpunkt und in der Animation über eine Umdrehung der Welle dargestellt ist. Das Bild zeigt einen Querschnitt durch die Lagermitte. Der Druckverlauf wurde mit der erweiterten Reynoldsschen Gleichung berechnet. Die rote Fläche im Schmierspalt stellt den Anteil der Schmierflüssigkeit und die gelbe Fläche den Anteil der gasförmigen Phase des Schmiermittel-Gas-Gemischs dar.
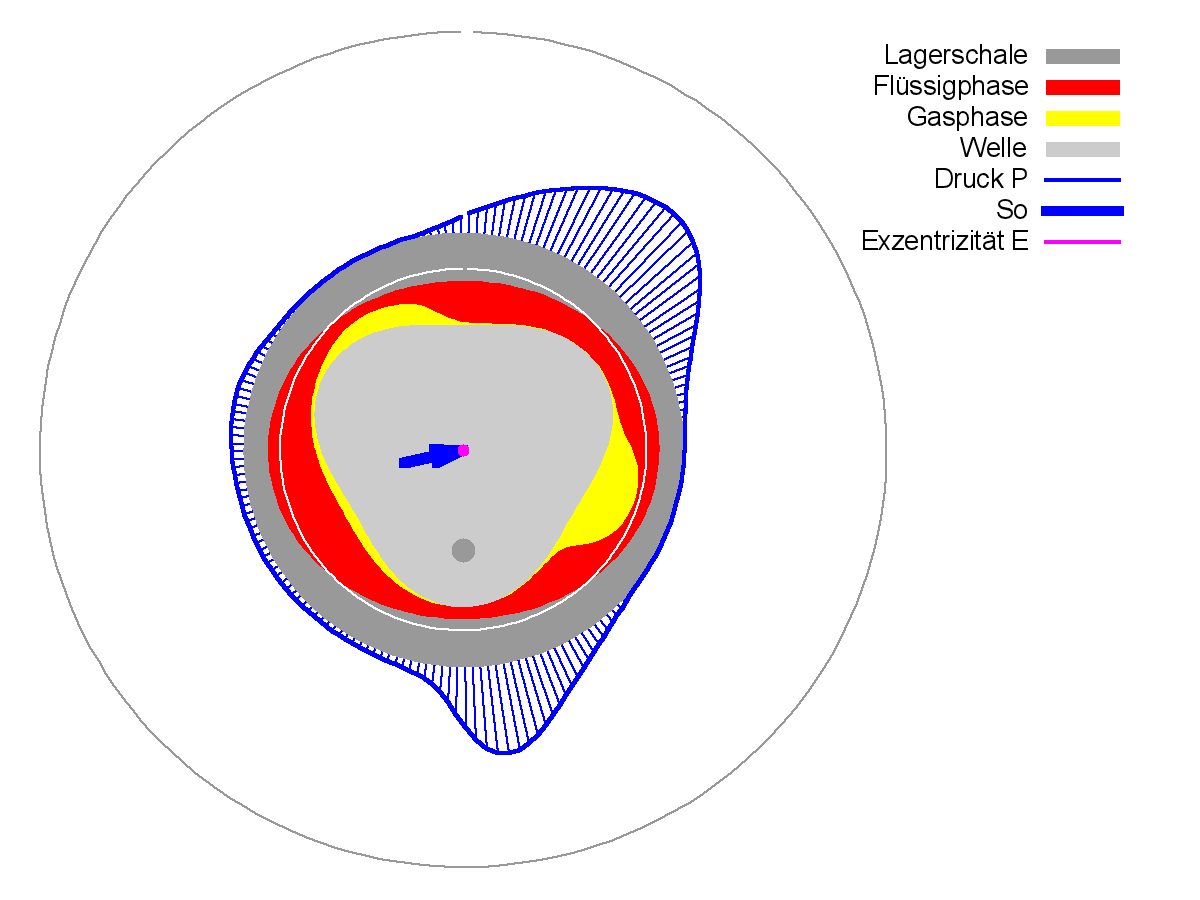
Bild 2.123: Druckverlauf, Spaltgeometrie und Ölverteilung im Lager mit elliptischer Lagerschale und "dreieckiger" Welle in konzentrischer Lage (Exzentrizität E(T)=0) (Animation)
zurück
weiter
zur dimensionsbehafteten Darstellung
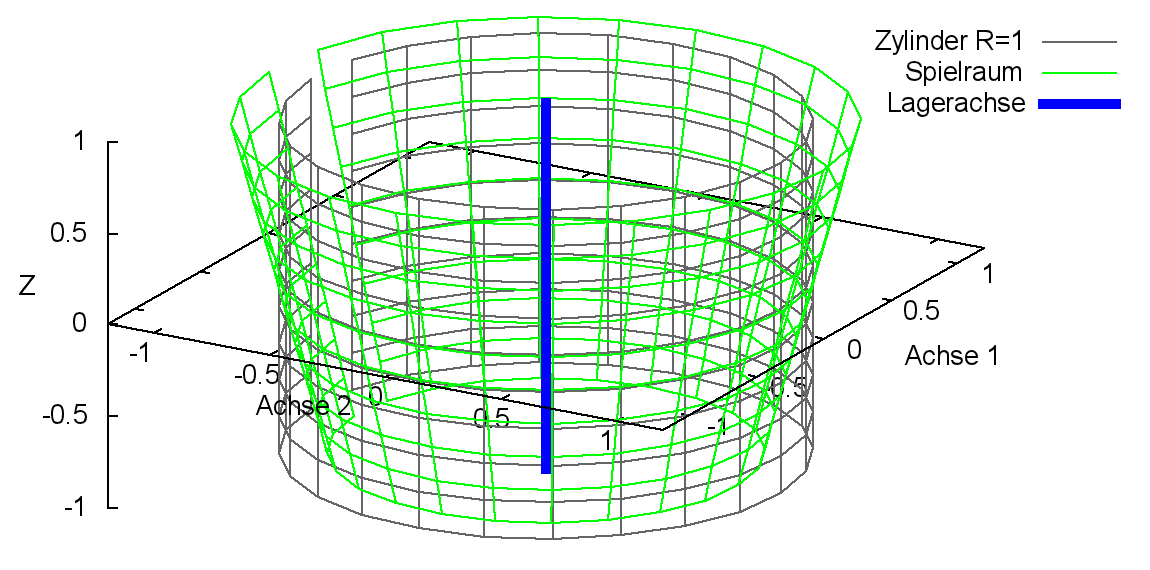
2.2.2.12 Dimensionslose konische Lagerschale
Bild 2.125 zeigt links den Spielraum (grün) eines Lagers mit einer konischen Lagerschale mit positiver Konizität KoLa und rechts den Spielraum mit negativer Konizität. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
Bild 2.125: Dimensionsloser Spielraum eines Lagers mit positiv konischer Lagerschale (links) und negativer Konizität (rechts)
Die maximale konische Formabweichung wird begrenzt auf
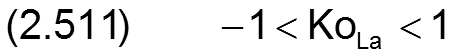
Der Betrag der Konizität koLa der Welle wird in folgender Weise dimensionslos gemacht
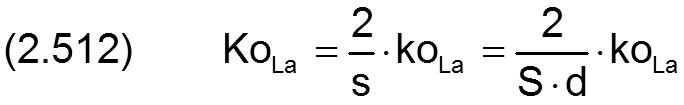
Die Änderung ΔH6 der dimensionslosen Spalthöhe H infolge einer konischen Welle wird berechnet durch

Die zugehörigen partiellen Ableitungen sind gegeben durch
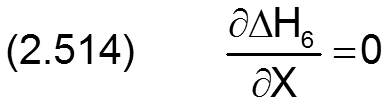
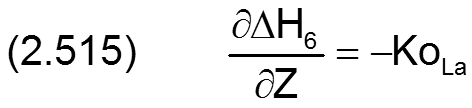
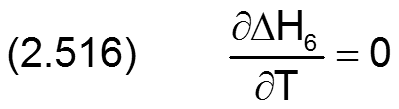
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.13 Dimensionslose konische Welle
Bild 2.127 zeigt links den Spielraum (grün) eines Lagers mit einer konischen Welle mit positiver Konizität KoWe und rechts den Spielraum mit negativer Konizität. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
Bild 2.127: Dimensionsloser Spielraum eines Lagers mit positiv konischer Welle (links) und negativer Konizität (rechts)
Die maximale konische Formabweichung wird begrenzt auf
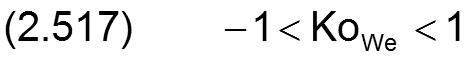
Der Betrag der Konizität koWe der Welle wird in folgender Weise dimensionslos gemacht
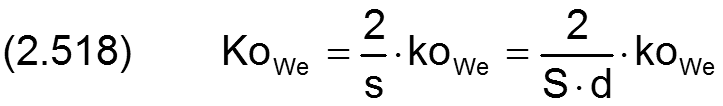
Die Änderung ΔH7 der dimensionslosen Spalthöhe H infolge einer konischen Welle wird berechnet durch

Die zugehörigen partiellen Ableitungen sind gegeben durch
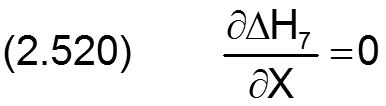


zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.14 Dimensionslose ballige Lagerschale
Bild 2.129 zeigt links den Spielraum (grün) eines Lagers mit einer balligen Lagerschale mit positiver Balligkeit BaLa und rechts den Spielraum mit negativer Balligkeit. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
Bild 2.129: Dimensionsloser Spielraum eines Lagers mit positiv balliger Lagerschale (links) und negativer Balligkeit (rechts)
Die maximale ballige Formabweichung wird begrenzt auf

Der Wert der Balligkeit baLa der Lagerschale wird in folgender Weise dimensionslos gemacht
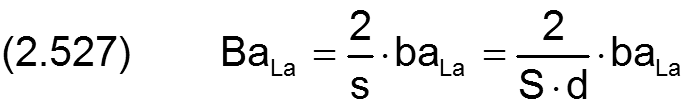
Die Änderung ΔH8 der dimensionslosen Spalthöhe H infolge einer balligen Lagerschale wird berechnet durch
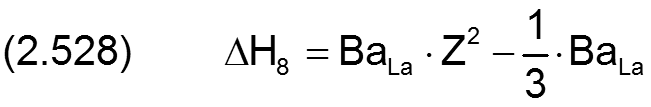
Die zugehörigen partiellen Ableitungen sind dann gegeben durch
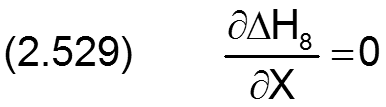
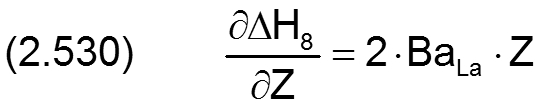
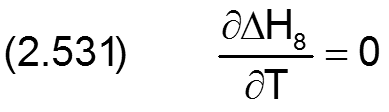
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.15 Dimensionslose ballige Welle
Bild 2.131 zeigt links den Spielraum (grün) eines Lagers mit einer balligen Welle mit positiver Balligkeit BaWe und rechts den Spielraum mit negativer Balligkeit. Zum Vergleich ist als graues Gitternetz der Spielraum des ideal zylindrischen Lagers eingeblendet.
Bild 2.131: Dimensionsloser Spielraum eines Lagers mit positiv balliger Welle (links) und negativer Balligkeit (rechts)
Die maximale ballige Formabweichung wird begrenzt auf
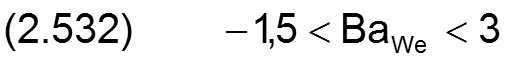
Der Wert der Balligkeit baWe der Welle wird in folgender Weise dimensionslos gemacht
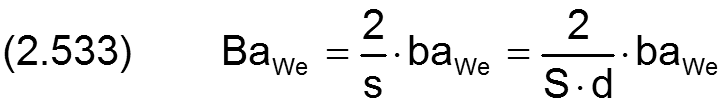
Die Änderung ΔH9 der dimensionslosen Spalthöhe H infolge einer balligen Welle wird berechnet durch
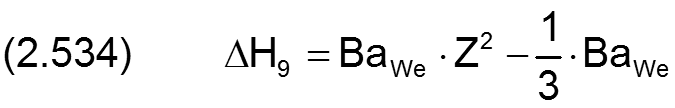
Die zugehörigen partiellen Ableitungen sind dann gegeben durch
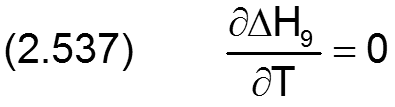
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.16 Lager mit versetzten Lagerabschnitten (Lagerversatz) in dimensionsloser Form
Die Parameter zur Definition des "Lagerversatzes" werden in folgender Weise dimensionslos gemacht:
Achsversatz
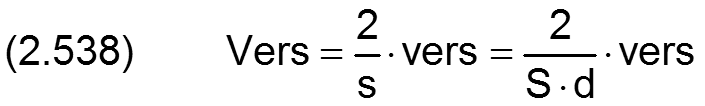
Breite des Lagerabschnitts 1
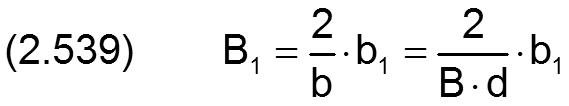
Breite des Lagerabschnitts 2
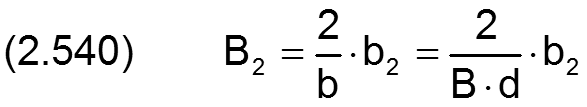
Es müssen für jeden Lagerabschnitt und die Übergänge gesonderte Formeln hergeleitet werden. Gemäß Bild 2.135 ergeben sich dabei 5 verschiedene Fälle.
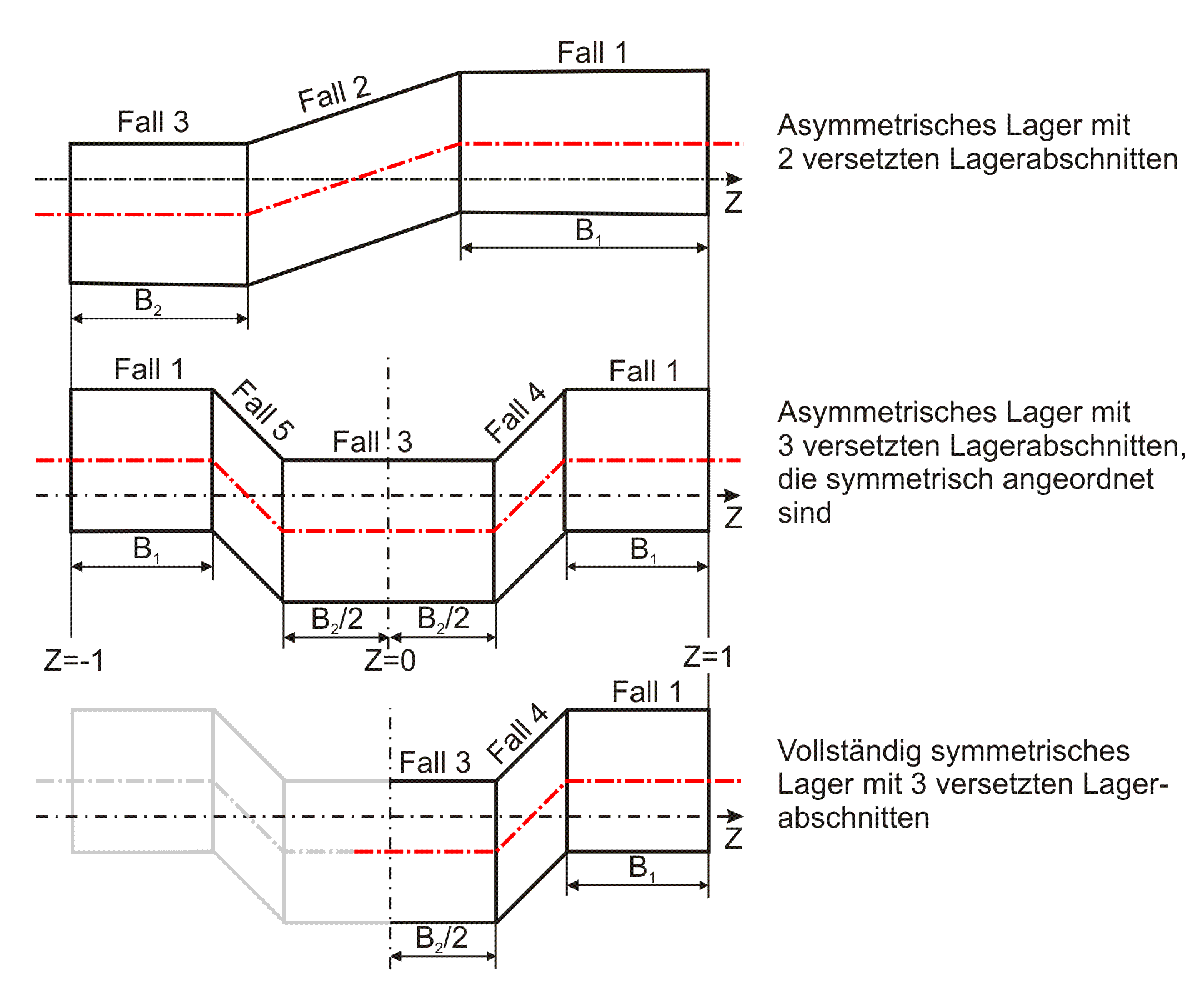
Bild 2.135: Zuordnung der Formeln zur Berechnung der Formabweichungen ΔH10 zu den verschiedenen Lagerabschnitten und Übergängen
Die Änderung ΔH10 der dimensionslosen Schmierspalthöhe über die Spaltfläche und die Zeit derartiger Formabweichungen lassen sich durch folgende Formeln beschreiben.
Fall 1:
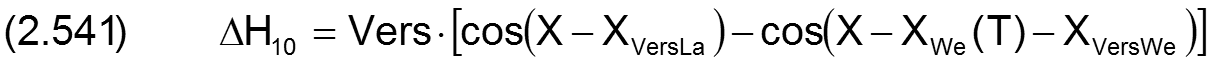
Die zugehörigen partiellen Ableitungen sind gegeben durch
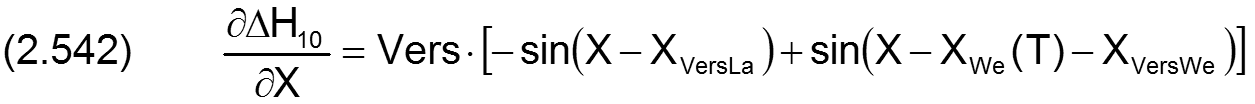
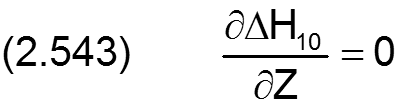

Fall 2:
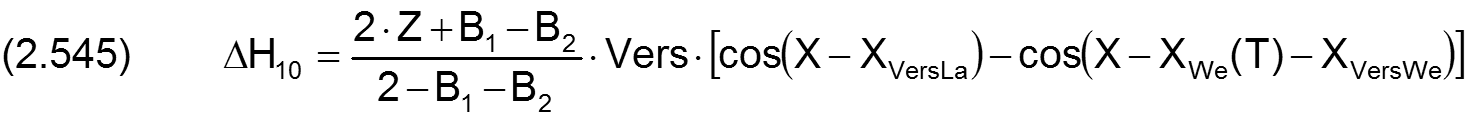
Die zugehörigen partiellen Ableitungen sind gegeben durch
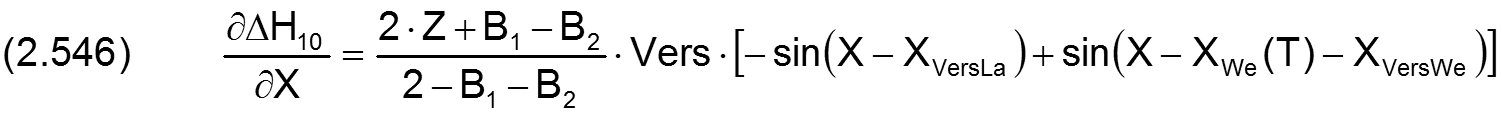

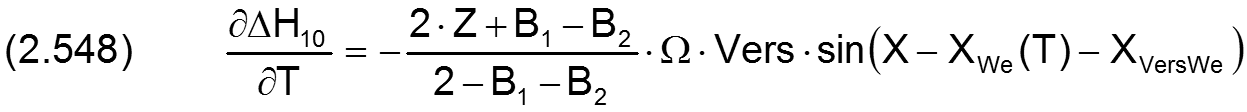
Fall 3:
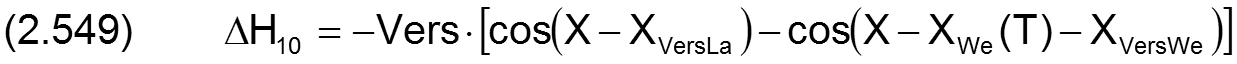
Die zugehörigen partiellen Ableitungen sind gegeben durch
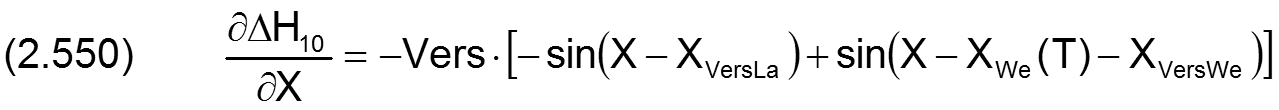

Fall 4:
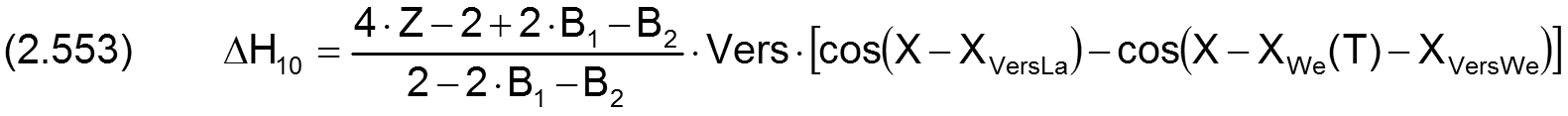
Die zugehörigen partiellen Ableitungen sind gegeben durch
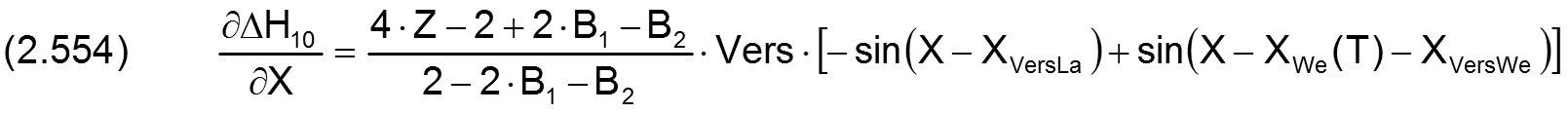
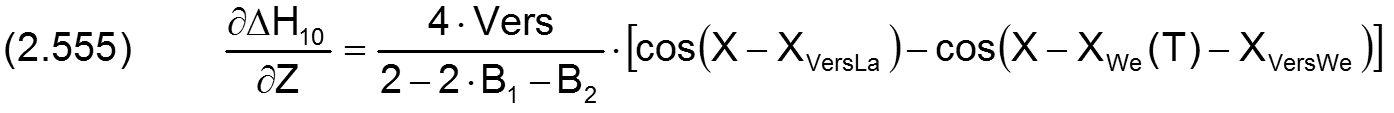

Fall 5:
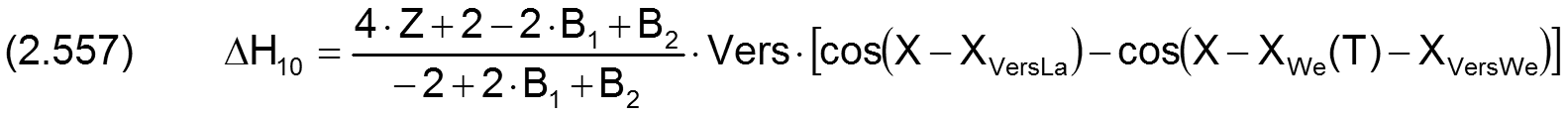
Die zugehörigen partiellen Ableitungen sind gegeben durch
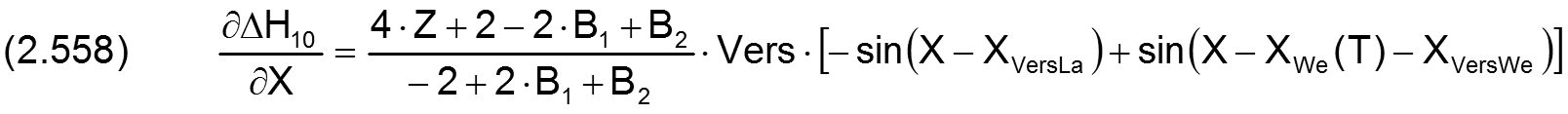
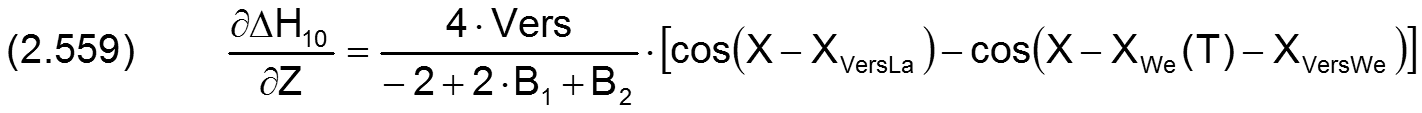
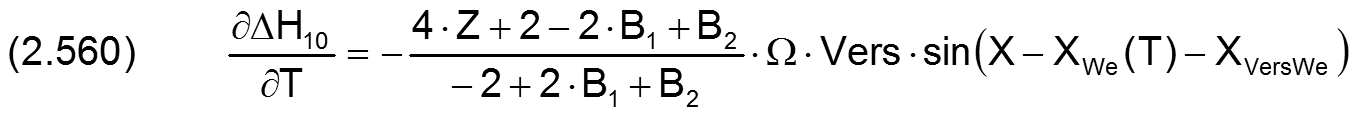
Siehe hierzu auch das Demonstrationsbeispiel Demo14 (Abschnitt 4.8.14).
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.17 Elastische Lagerschale in dimensionsloser Form ( noch unbearbeitet)
HINWEIS: Der Berechnungsalgorithmus für die Berücksichtigung der elastischen Verformung ist noch nicht ausgereift und ist deshalb für die Anwendung noch nicht frei gegeben. Die bereits implementierten Programmteile dazu sind deshalb bisher auch nur teilweise dokumentiert. Siehe dazu auch die Literaturquelle [
17].
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.18 Gesamte dimensionslose Spaltgeometrie
Die dimensionslose Gesamtspalthöhe H(X,Z,T) ist gegeben durch

Durch einsetzen der Gleichungen (2.427), (2.435), (2.456), (2.479), (2.490), (2.507), (2.513), (2.519), (2.528) und (2.534) ergibt sich die ausgeschriebene Gleichung für die Spalthöhe H

Die zugehörige partielle Ableitung ∂H/∂X sind gegeben durch

Durch einsetzen der Gleichungen (2.436), (2.457), (2.480), (2.500), (2.508), (2.514) und (2.520) ergibt sich die ausgeschriebene Gleichung
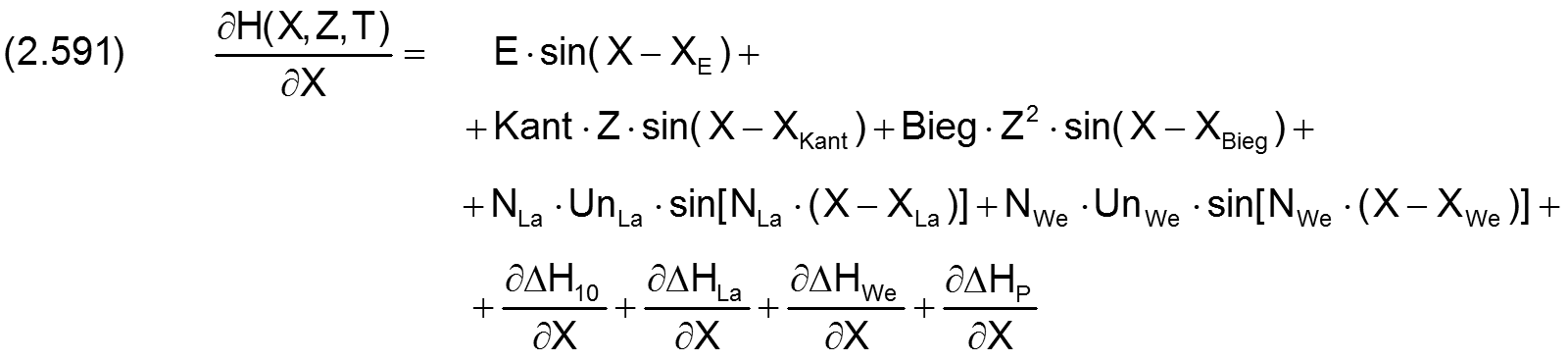
Die zugehörige partielle Ableitung ∂H/∂Z ist gegeben durch
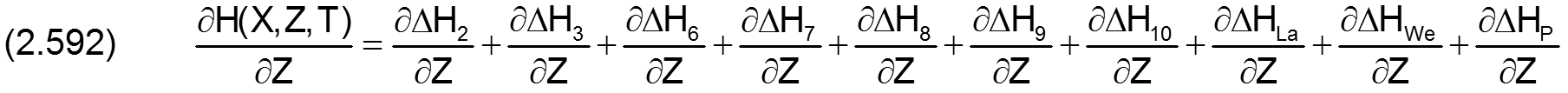
Durch einsetzen der Gleichungen (2.458), (2.481), (2.515), (2.521), (2.530) und (2.536) ergibt sich die ausgeschriebene Gleichung
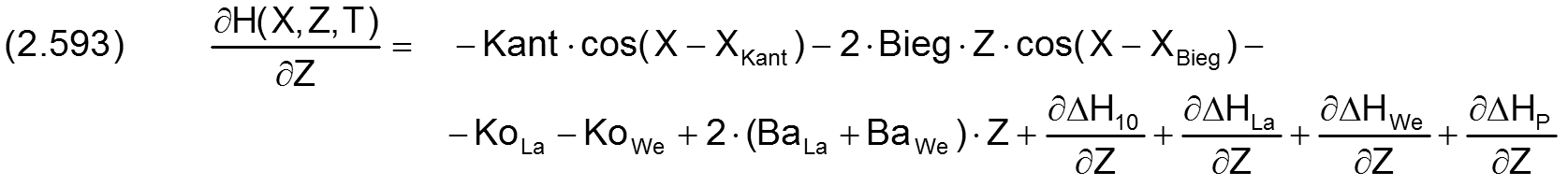
Die zugehörige partielle Ableitung dH/∂T ist gegeben durch

Durch einsetzen der Gleichungen (2.438), (2.459), (2.482), und (2.510) ergibt sich die ausgeschriebene Gleichung
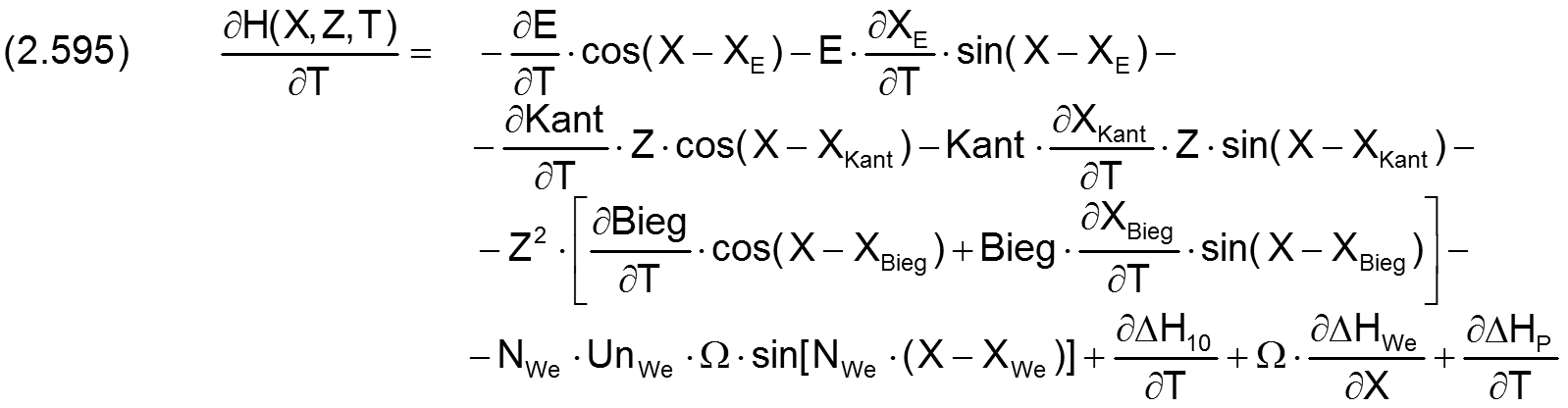
zurück
weiter
zur dimensionsbehafteten Darstellung
2.2.2.19 Dimensionsloses Gesamtvolumen des Schmierspalts
Passend zu den Volumenströmen im Schmierspalt wird das Spaltvolumen auf folgende Weise dimensionslos gemacht

Damit wird das dimensionslose Schmierspaltvolumen VolSpalt berechnet durch

Wird ein voll umschlossenes, starres Lager angenommen und sind keine beliebigen punktweise gegebenen Formabweichungen der Lagerschale oder der Welle gegeben, bzw. sind diese so angegeben, dass das angegebene Lagerspiel s auch weiterhin das mittlere Lagerspiel ist, dann vereinfacht sich die Formel.
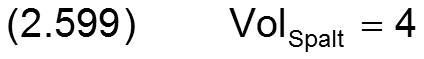
zurück weiter
.
.
.