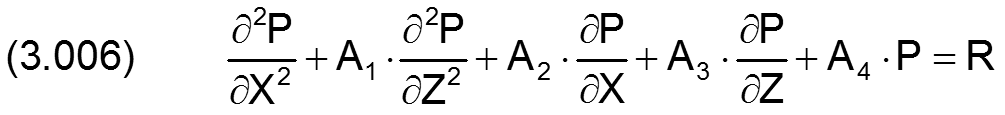
gegeben. Dabei ist P(Z,X) die gesuchte Funktion, über eine begrenzte Fläche der X-Z-Ebene, dem Definitionsbereich der Funktion. Die Koeffizienten A1, A2, A3, A4 und die rechte Seite R können berechenbare Funktionen von X und Z sein.
In den folgenden Unterabschnitten werden die wichtigsten, verwendeten nummerischen Lösungsmethoden unabhängig von ihrer Aufteilung auf die verschiedenen Routinen des Quelltextes des Programms erläutert.
zurück weiterDie Berechnung der Druckverteilung P(Z,X) im Schmierspalt bildet das Kernproblem der Berechnungen eines Gleitlagers. Diese Berechnung ist zu jedem Zeitpunkt JT mindestens einmal auszuführen. Dazu ist die Reynoldssche Differentialgleichung zu lösen. Weder für die klassische Reynoldssche Differentialgleichung, noch für ihre Erweiterung gibt es eine analytische Lösungsmethode. Deshalb muss ein numerisches Verfahren angewendet werden, welches eine Näherungslösung erzeugt.
zurück weiterDas Differenzenverfahren ist ein numerisches Verfahren, mit dem man lineare partielle Differentialgleichungen lösen kann. In unserem Fall ist eine lineare Differentialgleichung der Form
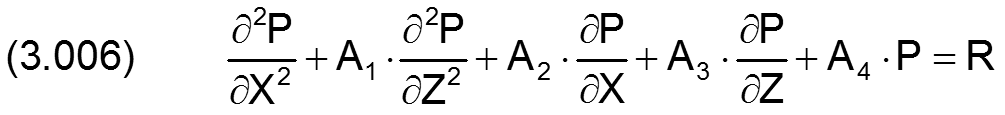
gegeben. Dabei ist P(Z,X) die gesuchte Funktion, über eine begrenzte Fläche der X-Z-Ebene, dem Definitionsbereich der Funktion. Die Koeffizienten A1, A2, A3, A4 und die rechte Seite R können berechenbare Funktionen von X und Z sein.
Am Rand des Definitionsbereiches sind Randbedingungen gegeben, die dafür sorgen, dass es genau eine Lösung für das Problem innerhalb der begrenzten Fläche gibt. In unserem Fall sind das der Umgebungsdruck an den Lagerrändern und die Drücke in den Schmiertaschen. Deshalb handelt es sich hier um ein Randwertproblem.
Das Differenzenverfahren funktioniert in der Weise, dass der Definitionsbereich mit einem diskreten Gitternetz überzogen wird und die Funktion P(Z,X) nur an den Gitterpunkten dieses Netzes berechnet wird. Die Tabelle dieser Werte stellt dann eine diskretisierte Näherungslösung dieses Problems dar.
Um dieses Problem numerisch lösbar zu machen, werden die partiellen Differentialquotienten ∂²P/∂X², ∂P/∂X, ∂²P/∂Z² und ∂P/∂Z näherungsweise durch Differenzenquotienten ersetzt. Dazu wird die Lösungsfunktion P(Z,X) jeweils im Bereich der zu berechnenden Stelle durch ein Polynom approximiert, dass sich auf dem gesuchten Gitterpunkt Z,X und mindesten zwei weiteren Nachbarpunkten abstützt. Durch drei auf einer Linie liegende Gitterpunkte ist eine quadratische Funktion der Form
![]()
eindeutig bestimmt. Außerdem sind damit auch ihre beiden Ableitungen bestimmt durch
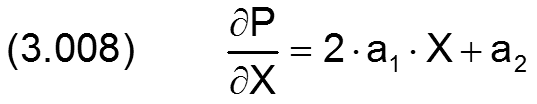
und
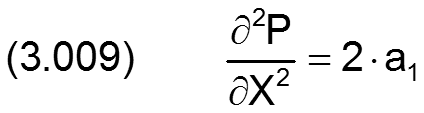
Daraus lassen sich dann die Formeln der benötigten Differenzengleichungen herleiten. Je nachdem, ob die drei Punkte mit konstanter oder variabler Schrittweite aufeinander folgen, ergeben sich verschiedene Differenzengleichungen. Im Programm SIRIUS werden die konstanten Schrittweiten X und Z verwendet. An den Lagerrändern und an den Rändern der Schmiertaschen ist der Abstand der Stützstellen aber nur ΔX/2 bzw. ΔZ/2. Deshalb werden im Programm die 3 Basisvarianten der entsprechenden Differenzengleichungen benötigt:
Basisvariante 1: Approximation über 3 Stützstellen mit der äquidistanten Schrittweite ΔX gemäß Bild 3.16.
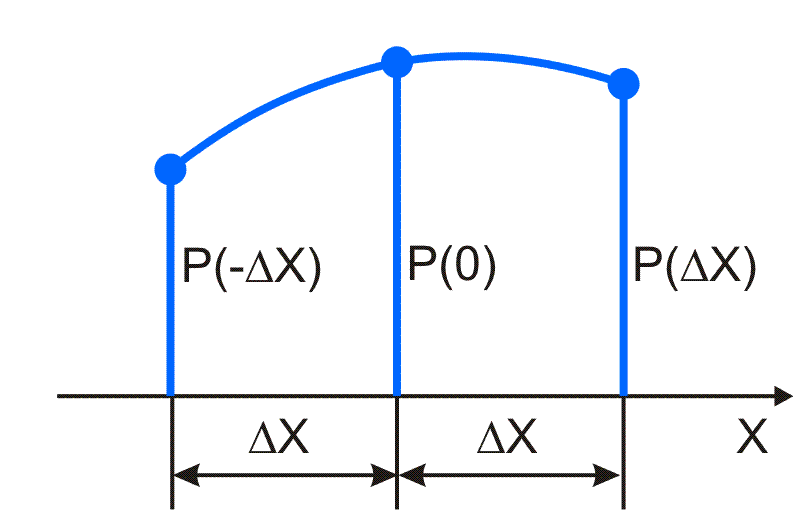 Bild 3.16: Basisvariante 1 |
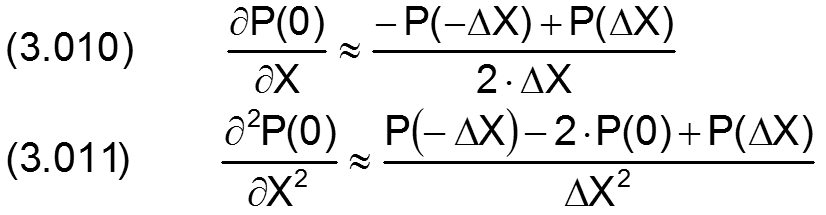 |
Basisvariante 2: Approximation über 3 Stützstellen mit den 2 Schrittweiten ΔX/2 und ΔX gemäß Bild 3.17.
 Bild 3.17: Basisvariante 2 |
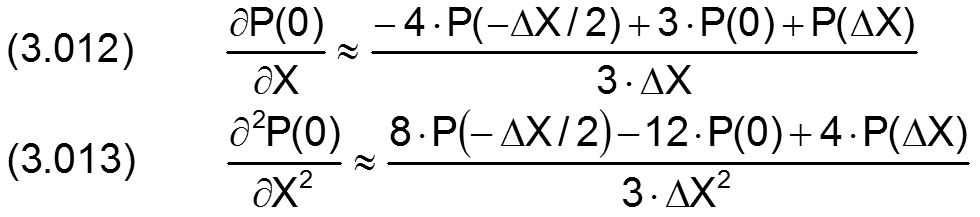 |
Basisvariante 3: Approximation über 3 Stützstellen mit den 2 Schrittweiten ΔX und ΔX/2 gemäß Bild 3.18.
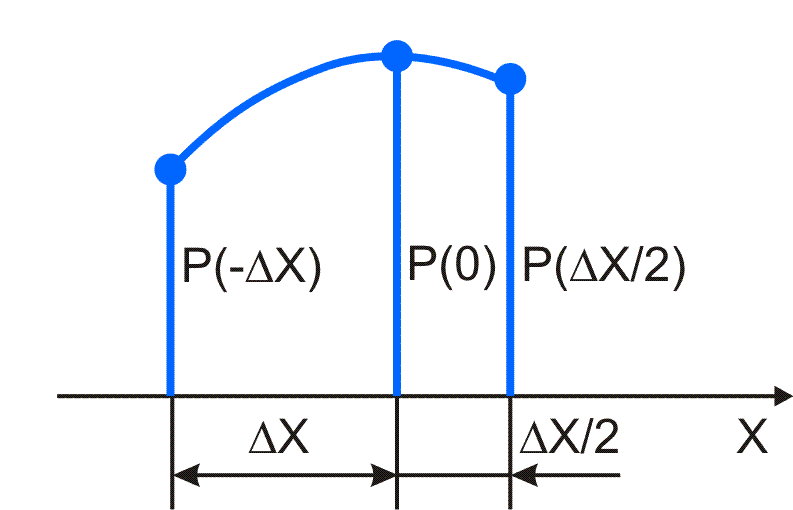 Bild 3.18: Basisvariante 3 |
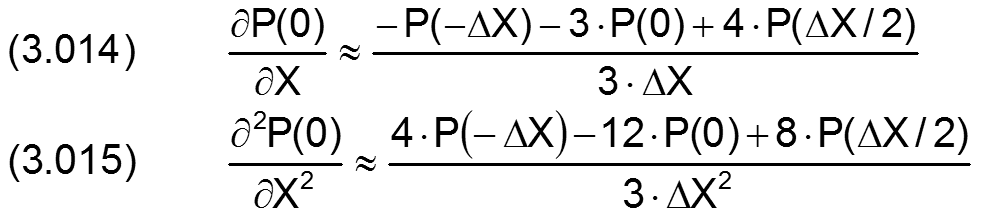 |
Die Differenzengleichungen in Z-Richtung werden analog gebildet.
Z.B. für den Fall, dass für den aktuell untersuchten Punkt P(0,0) und seine benachbarten Punkte die äquidistanten Schrittweiten ΔX und ΔZ gelten, kann die lineare Differentialgleichung (3.006) durch die lineare Differenzengleichung approximiert werden.

So lässt sich für jeden Gitterpunkt innerhalb des Definitionsbereichs eine lineare Gleichung aufstellen und es entsteht ein lineares Gleichungssystem, das sich mit einem geeigneten Lösungsverfahren für lineare Gleichungssysteme lösen lässt.
Die dimensionslose klassische Reynoldssche Differentialgleichung (siehe Abschnitt 2.2.3.1) ist eine lineare partielle Differentialgleichung 2.Ordnung.
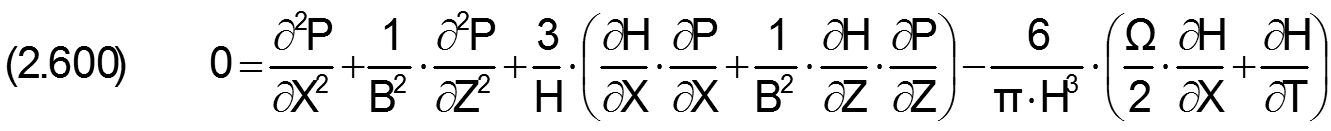
Sie hat die lineare Struktur
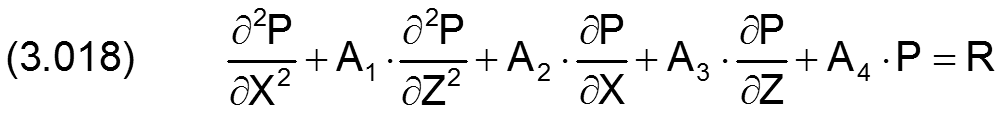
Die Randbedingungen sind die Drücke an den Schmierspalträndern und den Schmiertaschenrändern.
Das Differenzenverfahren ist hierfür geeignet und das Problem kann damit direkt gelöst werden. Die Felder der Koeffizienten A1(NGlei) bis A4(NGlei) und die rechten Seiten R(NGlei) für jedes Flächenelement (JZ,JX) des eigentlichen Schmierspalts werden durch die Routine "KoeDGL3" berechnet.
Die Berechnung des Druckverlaufs im Schmierspalt mit der klassischen Reynoldsschen Differentialgleichung wird durch die Routine "FilmDruck1" ausgeführt.
zurück weiterDie dimensionslose erweiterte Reynoldssche Differentialgleichung (Abschnitt 2.2.3.2) ist nicht mehr linear.
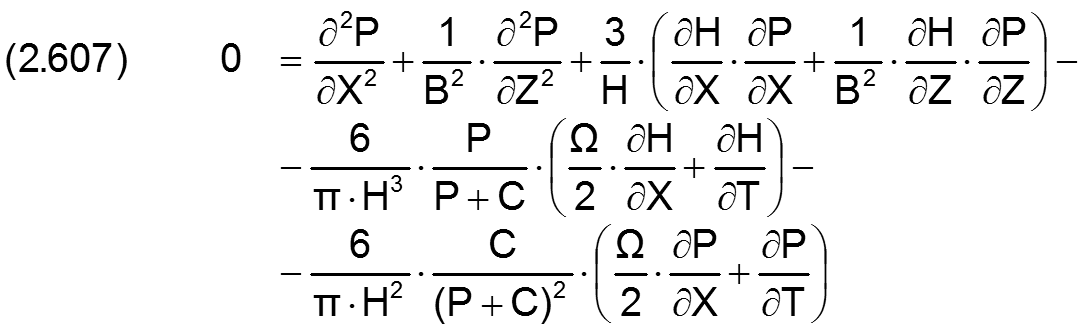
Sie ist eine nichtlineare partielle Differentialgleichung 2.Ordnung. Bezogen auf die Ortskoordinaten X und Z handelt es sich hier wieder um ein Randwertproblem und bezogen auf die Zeitkoordinate T um ein Anfangswertproblem.
Das Differenzenverfahren ist nur für lineare Gleichungen geeignet. Um das bewährte Verfahren auch hier anwenden zu können, wird deshalb die nicht lineare Differentialgleichung durch eine linearisierte Näherung ersetzt. Ausgehend von geschätzten Anfangsnäherungswerten Pn für den Druck P kann so über mehrere Iterationsschritte auch dieses Problem mit Hilfe des Differenzenverfahrens gelöst werden. Dabei wird in folgender Weise vorgegangen: Zunächst wird durch Extrapolation aus der Druckverteilung im Schmierspalt des vorhergehenden Zeitpunktes JT-1 eine erste Näherung Pn für den Zeitpunkt JT geschätzt. Anschließend wird über NI Iterationszyklen durch Anwendung des Differenzenverfahrens auf die linearisierte Differentialgleichung die Näherungslösung verbessert. Es hat sich gezeigt, dass üblicherweise nach der Extrapolation 3 Iterationszyklen ausreichend sind. Deshalb ist im Programm NI=3 vorgegeben. Der Parameter NI kann im Eingabemenü 4.4.12.3 "Programminterne Parameter bearbeiten" verändert werden, wovon aber in der Regel abzuraten ist. Dieser Iterationszyklus ist in den Bildern 3.04, und 3.06 als grüne Schleife dargestellt. Etwas detailierter ist er außerdem in der Übersichtsdarstellung des Flussdiagramms der Routine "FilmDruck2" (Bild 3.10 rechtes Diagramm) dargestellt.
Durch die Linearisierung wird die erweiterte Reynoldssche Differentialgleichung in die lineare Form gebracht
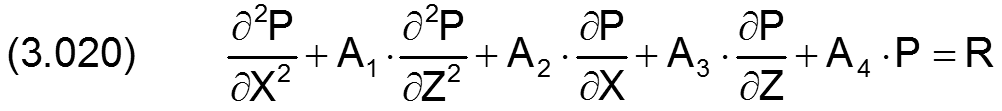
wobei
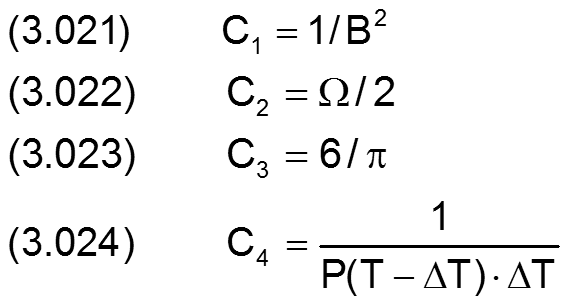
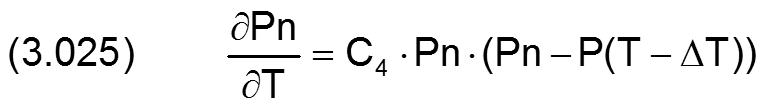


Pn ist hier die vorhergehende Näherung für den Druck P. Ausführlich erläutert ist die Linearisierung in [20, Abschnitt 7.3].
Die Felder der Koeffizienten A1(NGlei) bis A4(NGlei) und die rechten Seiten R(NGlei) für jedes Flächenelement (JZ,JX) des eigentlichen Schmierspalts werden durch die Routine "KoeDGL7" berechnet.
Die iterative Berechnung des Druckverlaufs im Schmierspalt mit der linearisierten erweiterten Reynoldsschen Differentialgleichung wird durch die Routine "FilmDruck2" ausgeführt.
zurück weiterUm das Differenzenverfahren anwenden zu können, muss die kontinuierliche Funktion der Druckverteilung im Schmierspalt diskretisiert werden. Gemäß Bild 3.19 wird die Fläche des abgewickelten Schmierspalts in NX·NZ Flächenelemente der Größe ΔX·ΔZ aufgeteilt. Im gezeigten Beispiel handelt es sich um ein voll umschlossenes (Vollum=1), symmetrisches (Sym=1) Lager.
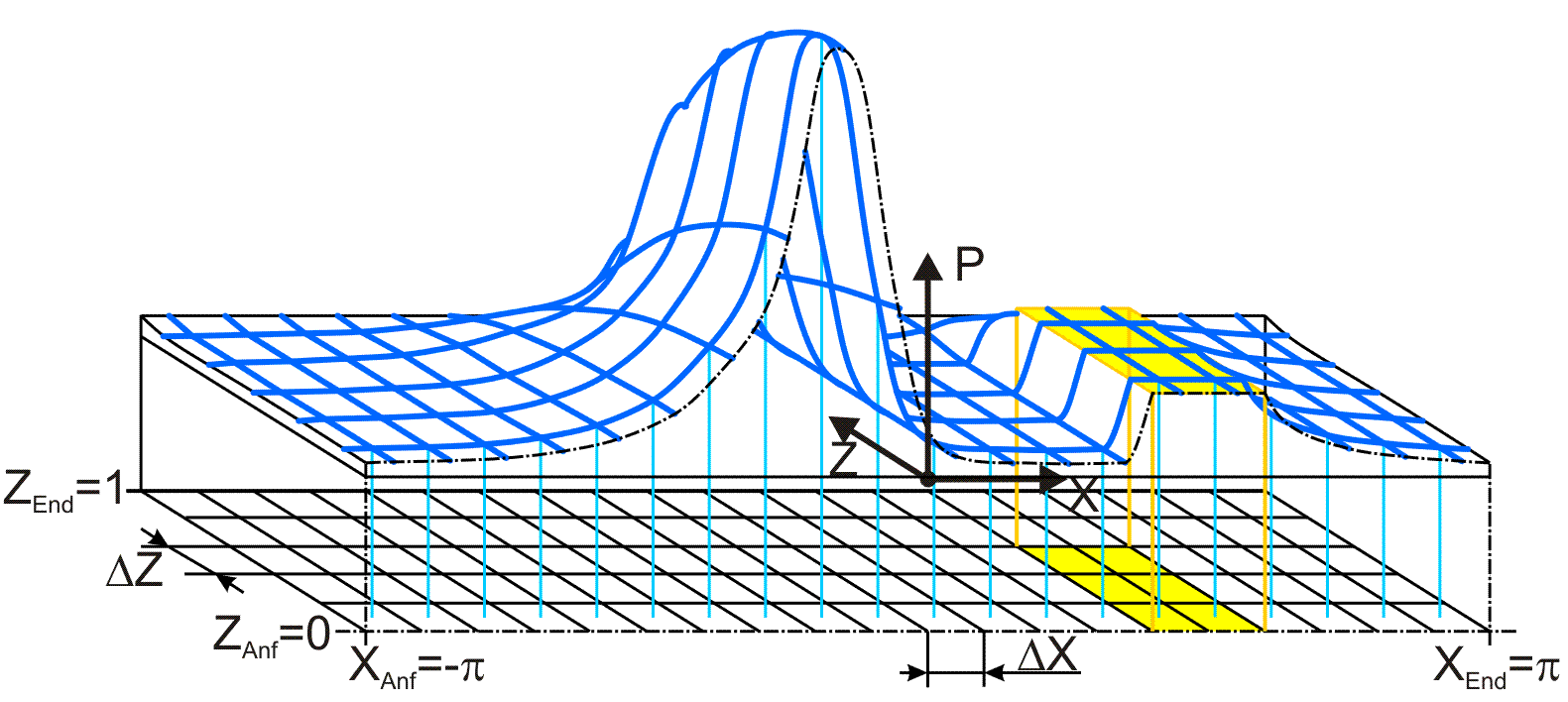
Bild 3.19: Diskretisierung der Schmierspaltfläche in NX·NZ Flächenelemente
Die Drücke P(JZ,JX) werden jeweils für die Mitte des Flächenelements (JZ,JX) berechnet (hellblaue Stützstellen). Mit dem dunkelblauen Liniennetz ist hier die Druckverteilung im Schmierspalt skizziert. Der Druckverlauf zwischen den berechneten Stützstellen wird durch Parabelbögen approximiert.
Die gelbe Fläche im Bild 3.19 zeigt die Ausdehnung einer Schmiertasche. Die freie Wahl der Anordnung von Schmiertaschen ist lediglich dadurch eingeschränkt, dass der Verlauf der Taschenränder immer entlang der Grenzen der Flächenelemente angenommen wird. Innerhalb der gesamten Taschenfläche wird ein konstanter Druck angenommen. Das wird durch entsprechende Approximationsgleichungen berücksichtigt. Siehe dazu Abschnitt 3.4.1.6.
Mit dem Grafikprogramm GNUPLOT können die berechneten Druckverteilungen im Schmierspalt schnell dargestellt werden, wobei auf die Gitterteilung der Berechnung zurückgegriffen wird. Es ist dabei jedoch zu beachten, dass hier die Darstellung, bedingt durch die Eigenheiten des Programms GNUPLOT, etwas vereinfacht und teilweise eingeschränkt ist. Bild 3.20 zeigt den Druckverlauf für das Beispiel aus Bild 3.19 in der Darstellung mit GNUPLOT.
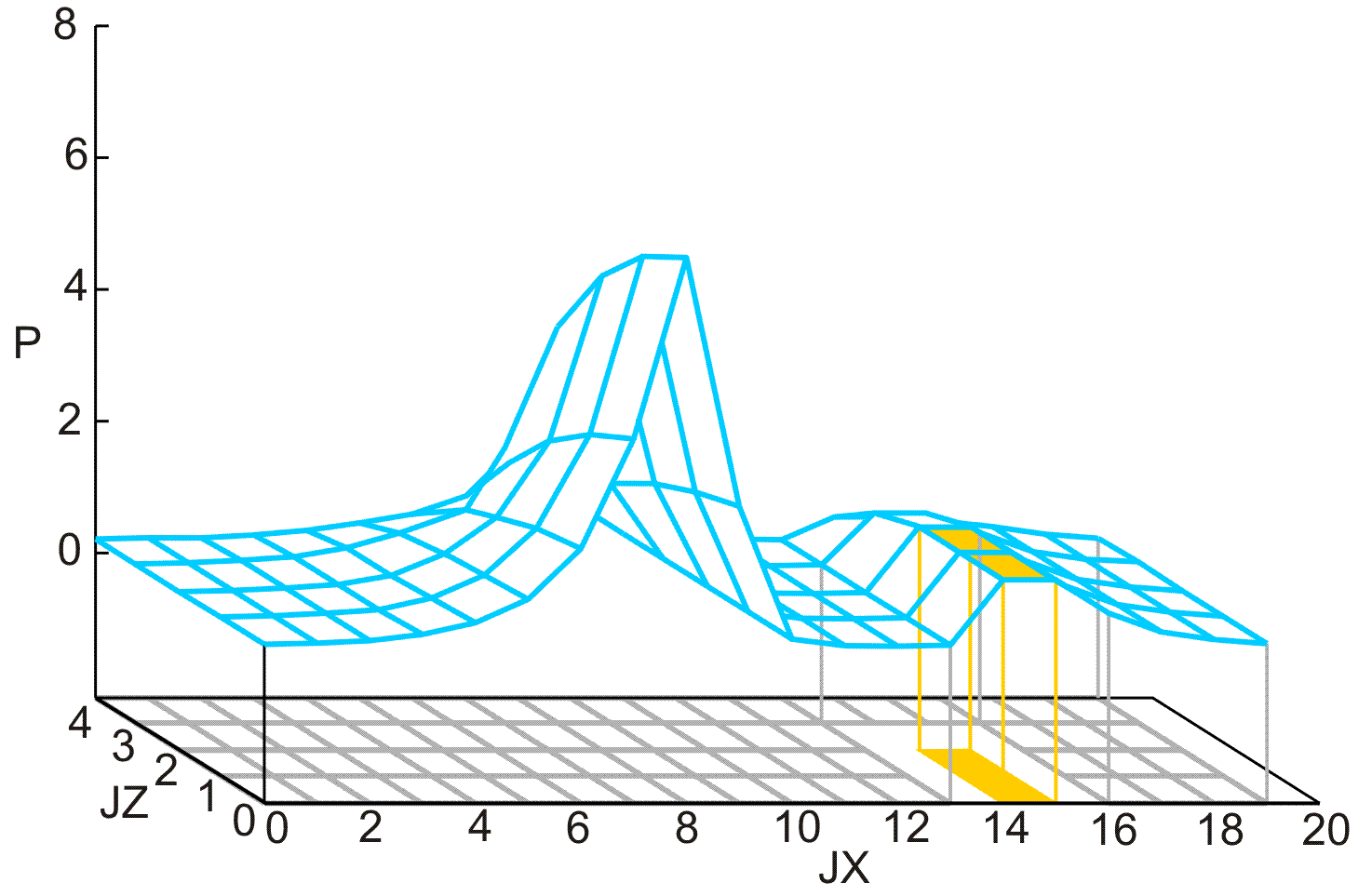
Bild 3.20: Darstellung der Druckverteilung im Schmierspalt mit dem Grafikprogramm GNUPLOT
Hier werden lediglich die berechneten Drücke in den Mitten der Flächenelemente angezeigt, verbunden durch gerade Linien zu einem Gitternetz. Dadurch wird die Druckverteilung nicht exakt bis an den Lagerrand dargestellt. Es fehlt rundherum jeweils die Breite eines halben Flächenelements und die Zählung der Gitterpunkte beginnt nicht wie in der Berechnung mit 1 sondern mit 0. Das in GNUPLOT gezeigte Gitternetz (grau) zeigt nicht die Flächenelemente, die der Berechnung zugrundeliegen, sondern die Verbindungslinien der Elementmitten. Die berechneten Druckwerte liegen deshalb hier über den Schnittpunkten des GNUPLOT-Gitternetzes.
Insbesondere die Darstellung der Schmiertaschen kann durch diese vereinfachte Darstellung bei einem kritischen Beobachter evtl. zu Irritationen führen. Während in der Darstellung der Druckverteilung die Schmiertasche als Fläche mit einem konstanten Druck (orange Fläche) um jeweils eine Flächenelementbreite zu klein dargestellt wird, erscheint die Schmiertasche in dem darunter liegenden Gitternetz um eine Flächenelementbreite zu groß.
Die Überlagerung der beiden oben gezeigten Bilder im Bild 3.21 soll diese Unterschiede noch einmal verdeutlichen.

Bild 3.21: Überlagerung der grafischen Darstellungen aus Bild 3.19 und 3.20
In dieser Darstellung stellen die gelben Flächen wieder die wahre Größe der Schmiertasche dar und die genauere Darstellung der Druckverteilung aus Bild 3.19 ist hier mit dünnen schwarzen Linien dargestellt.
Bei der hier gewählten groben Gitterteilung von 20·5 Flächenelementen werden die Abweichung der mit GNUPLOT dargestellten Druckverteilung gegenüber der im Modell approximierten Druckverteilung deutlich. Je feiner jedoch die Gitterteilung gewählt wird, umso unbedeutender werden diese Abweichungen. Deshalb wurde auch darauf verzichtet, weiteren Aufwand in eine verbesserte Darstellung zu investieren.
Die Eingabe- und Ergebnisdaten zu dem hier gezeigten Beispiel sind im Demonstrationsbeispiel "Demo22" abgelegt.
zurück weiterNur wenn sich innerhalb des Schmierspaltes keine Schmiertaschen befinden und das Lager ausschließlich über den Lagerrand geschmiert wird, ist für alle NX·NZ Flächenelemente die Differenzengleichung aufzustellen. Falls im Lager Schmiertaschen angeordnet sind, sind deren Flächen aus dem eigentlichen Schmierspalt auszuschließen. Weil in den Schmiertaschen die Spalthöhe viel größer ist als im eigentlichen Schmierspalt, wird angenommen, dass der Druck über die Fläche einer Schmiertasche konstant ist und hier die Reynoldssche Gleichung deshalb nicht zur Anwendung kommt. Allerdings sind auch für die Berechnung der Drücke in den Schmiertaschen einige Gleichungen aufzustellen, was im Abschnitt 3.4.2 beschrieben wird.
Um die Lage und Ausdehnung der Schmiertaschen innerhalb der abgewickelten Spaltfläche zu erfassen, wurde das Steuerfeld KX eingerichtet, welches durch ein Feld von NZ·NX ganzen Zahlen die Anordnung der diskretisierten Flächenelemente abbildet. Alle Flächenelemente, die Teil einer Schmiertasche sind, werden mit einer negativen ganzen Zahl im Steuerfeld KX belegt, deren Betrag die Nummer der jeweiligen Schmiertasche codiert. Bild 4.020 zeigt das Steuerfeld KX eines symmetrischen, voll umschlossenen Lagers, dessen Spaltfläche in 25·10 Flächenelemente aufgeteilt wurde, mit 2 Schmiertaschen.
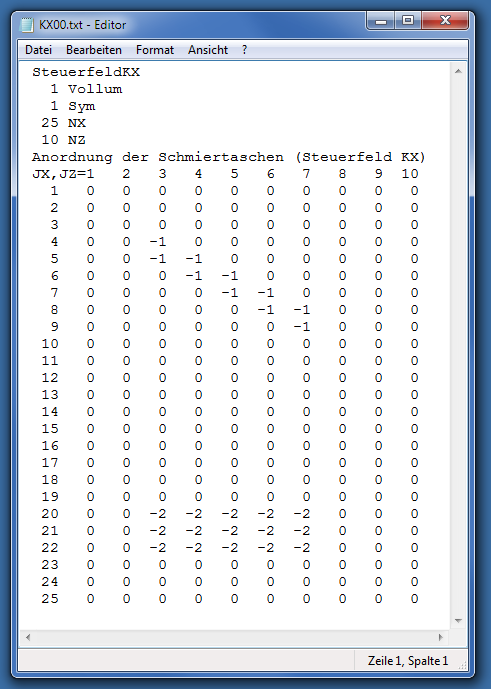
Bild 4.020: Beispiel eines Steuerfeldes KX mit NX=25 Zeilen, NZ=10 Spalten und 2 Schmiertaschen für ein voll umschlossenes, symmetrisches Lager, wie es in einer Textdatei abgespeichert ist
Schmiertaschen sowohl auf der Lagerschale als auch auf der Welle anzuordnen, ist im Programm nicht vorgesehen. Davon gibt es eine Ausnahme: Neben beliebig geformten und angeordneten Schmiertaschen auf einer Gleitfläche können auch Ringnuten, die das Lager vollständig umschließen, auf der anderen Gleitfläche angeordnet sein. Das ist möglich, weil es bei Ringnuten egal ist, auf welcher der beiden Gleitflächen des Lagers sie angeordnet sind. Ihre Wirkung auf die Schmiermittelströmung im Schmierspalt ist die gleiche. Deshalb können z.B. Ringnuten in der Wellenoberfläche einfach auf der Lagerschalenoberfläche modelliert werden.
Bild 3.23 zeigt zwei willkürliche Anordnungen von Schmiertaschen, links in einem voll umschlossenen, symmetrischen Lager und rechts in einem teilweise umschlossenen, asymmetrischen Lager. Anhand dieser zwei Beispiele soll die Verwendung aller erforderlichen Varianten von Differenzengleichungen gezeigt werden, die aus den Gleichungen (3.010 bis 3.015) der 3 Basisvarianten (Abschnitt 3.4.1.1) abgeleitet sind.
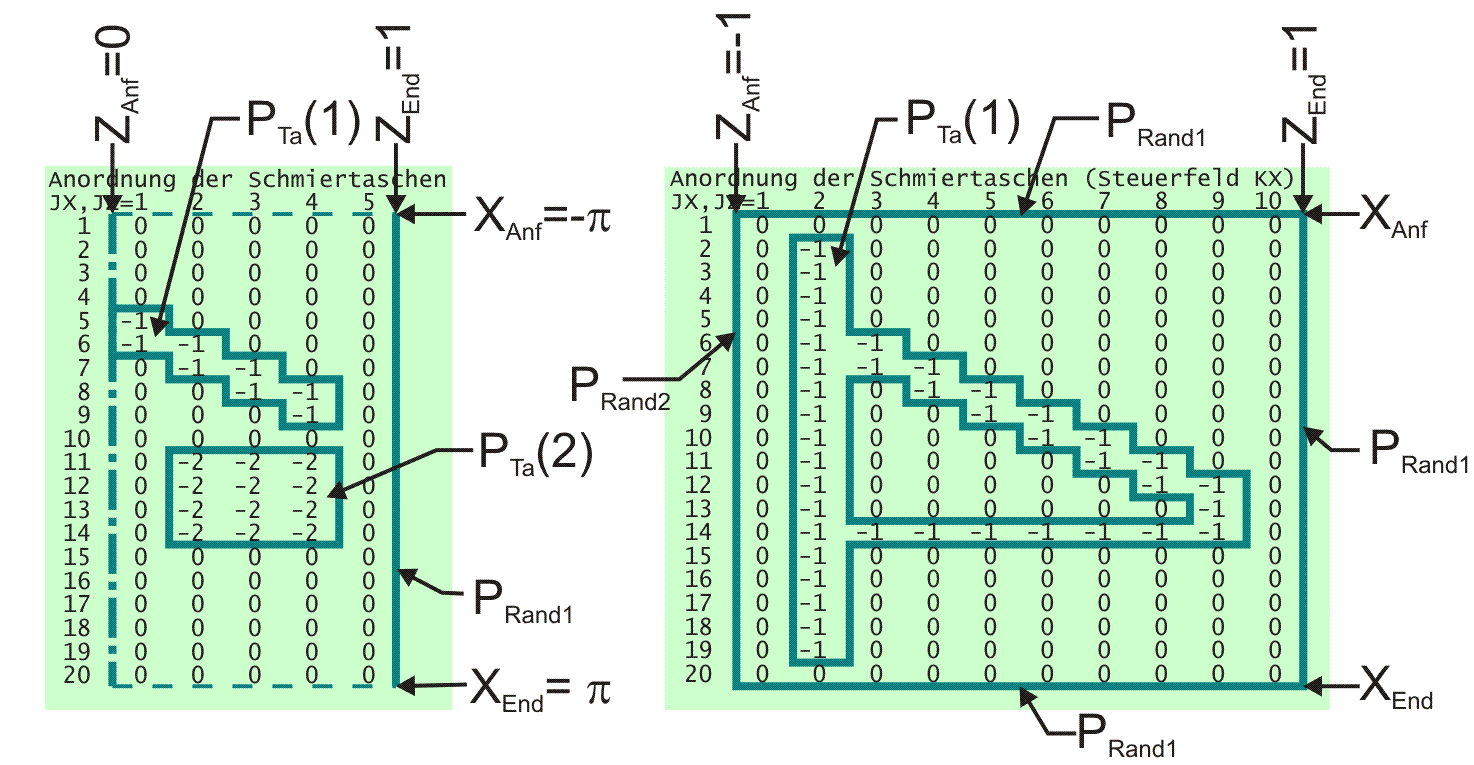
Bild 3.23: Zwei Varianten von Schmiertaschenanordnungen
Aus der Anordnung der Schmiertaschen ist ersichtlich, dass in Abhängigkeit von der Lage eines Flächenelements verschiedene Differenzengleichungen verwendet werden müssen. Für die Berechnung der partiellen Ableitungen in X-Richtung ergeben sich dabei 8 Varianten und für die Ableitungen in Z-Richtung ergeben sich 10 Varianten, die nachfolgend angegeben werden:
Variante 1: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in Richtung der entsprechenden Koordinatenachse an beiden Seiten an Flächenelemente des eigentlichen Schmierspalts. Bild 3.24 skizziert diesen Fall für die X-Richtung.
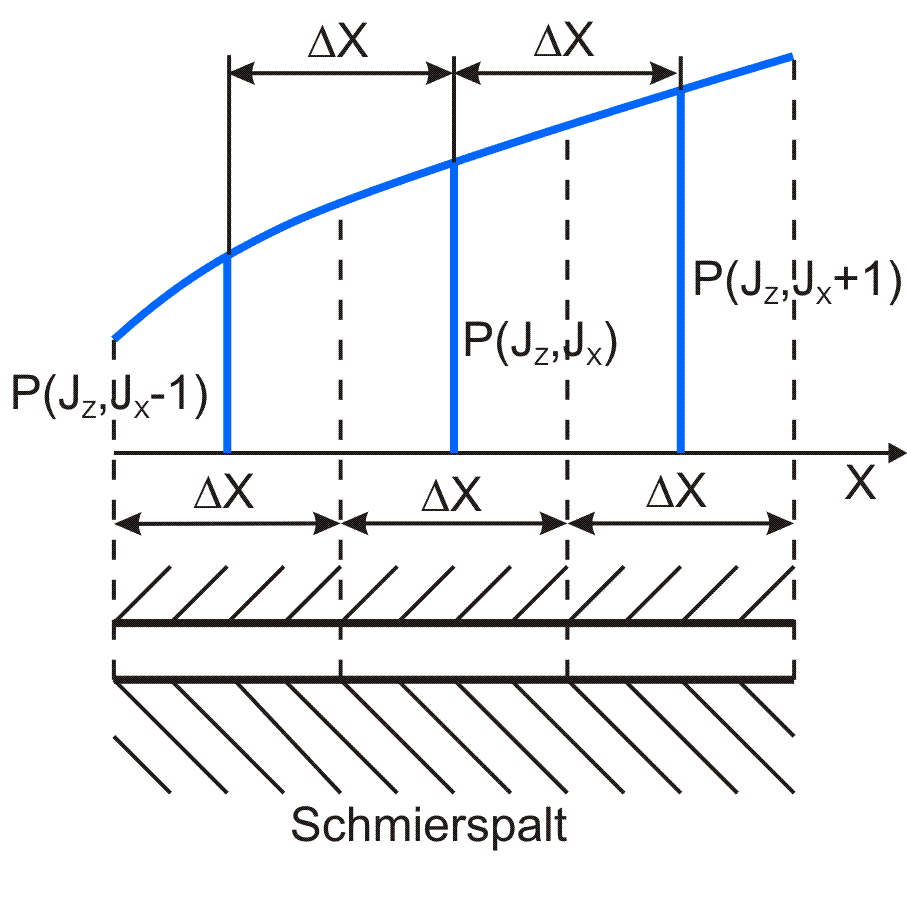 Bild 3.24: Skizze zu Variante 1 |
Für die partiellen Ableitungen in X-Richtung gilt
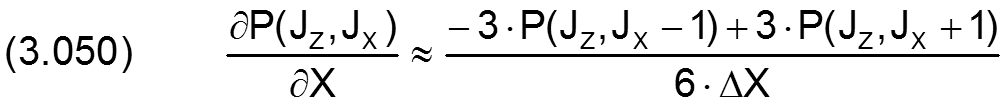
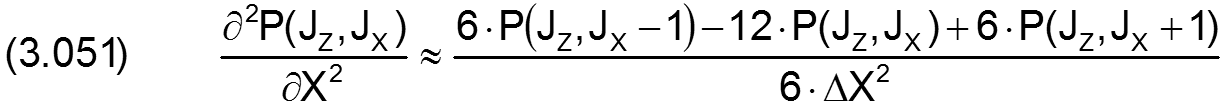 Für den analogen Fall in Z-Richtung gilt 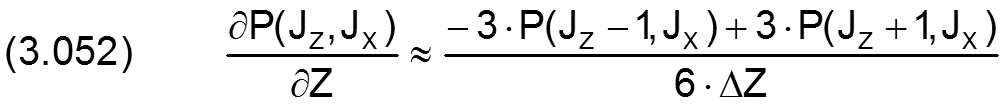
 |
Variante 2: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in negativer Richtung der Koordinatenachse an ein Flächenelement, das zu einer Schmiertasche gehört. Es wird angenommen, dass die Grenze zwischen Schmiertasche und Schmierspaltelement genau auf der Grenze zwischen den Flächenelementen liegt und im gesamten Flächenelement der Schmiertasche ein konstanter Druck herrscht. Bild 3.25 skizziert diesen Fall für die X-Richtung.
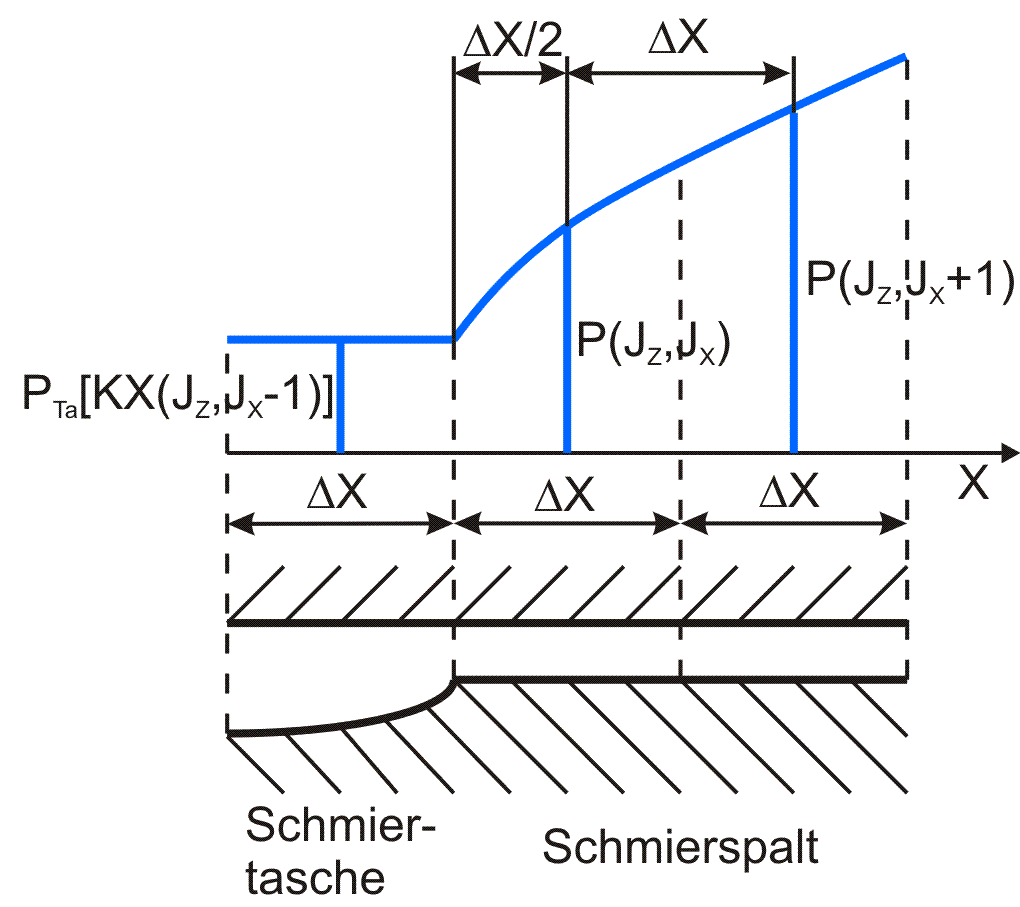 Bild 3.25: Skizze zu Variante 2 |
Für die partiellen Ableitungen in X-Richtung gilt
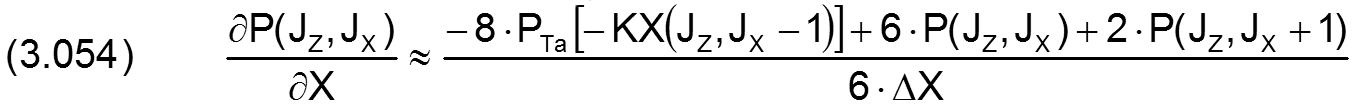
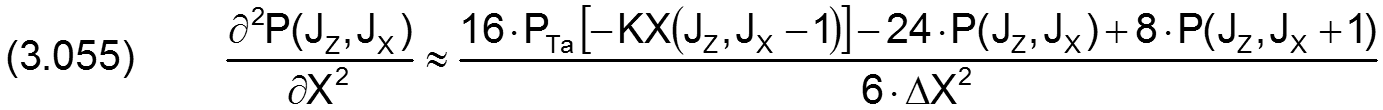 Für den analogen Fall in Z-Richtung gilt 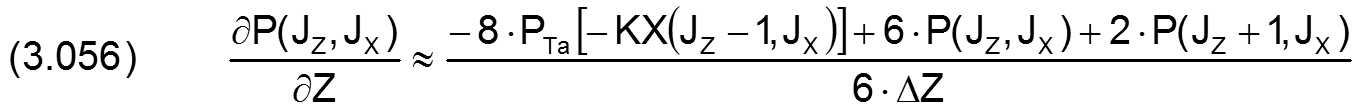
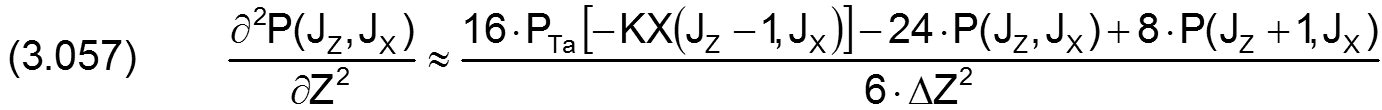 |
Variante 3: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in positiver Richtung der Koordinatenachse an ein Flächenelement, das zu einer Schmiertasche gehört. Es wird angenommen, dass die Grenze zwischen Schmiertasche und Schmierspaltelement genau auf der Grenze zwischen den Flächenelementen liegt und im gesamten Flächenelement der Schmiertasche ein konstanter Druck herrscht. Bild 3.26 skizziert diesen Fall für die X-Richtung.
 Bild 3.26: Skizze zu Variante 3 |
Für die partiellen Ableitungen in X-Richtung gilt
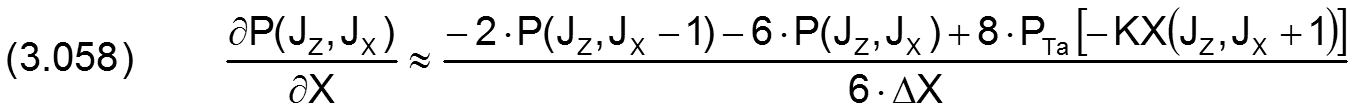
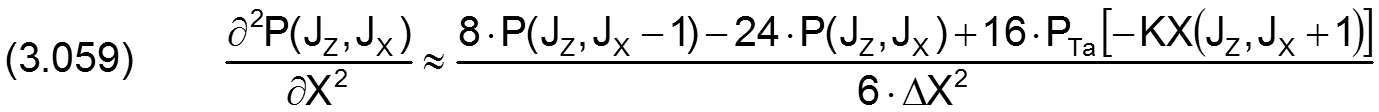 Für den analogen Fall in Z-Richtung gilt 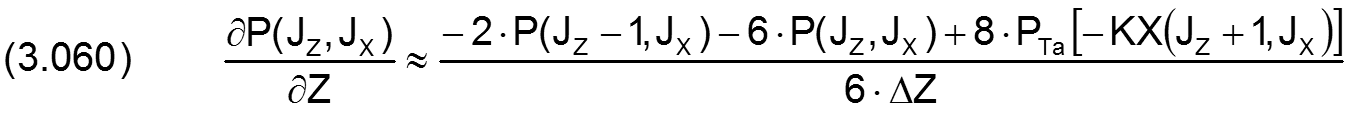
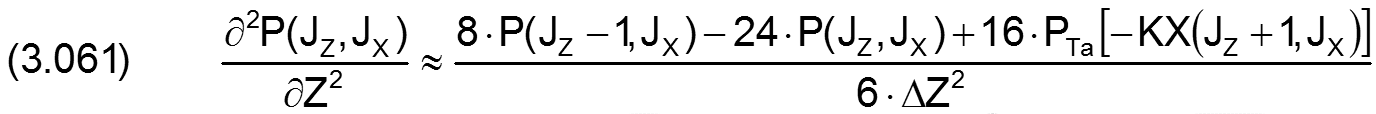 |
Variante 4: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in Richtung der entsprechenden Koordinatenachse an beiden Seiten an Flächenelemente von Schmiertaschen. Bild 3.27 skizziert diesen Fall für die X-Richtung.
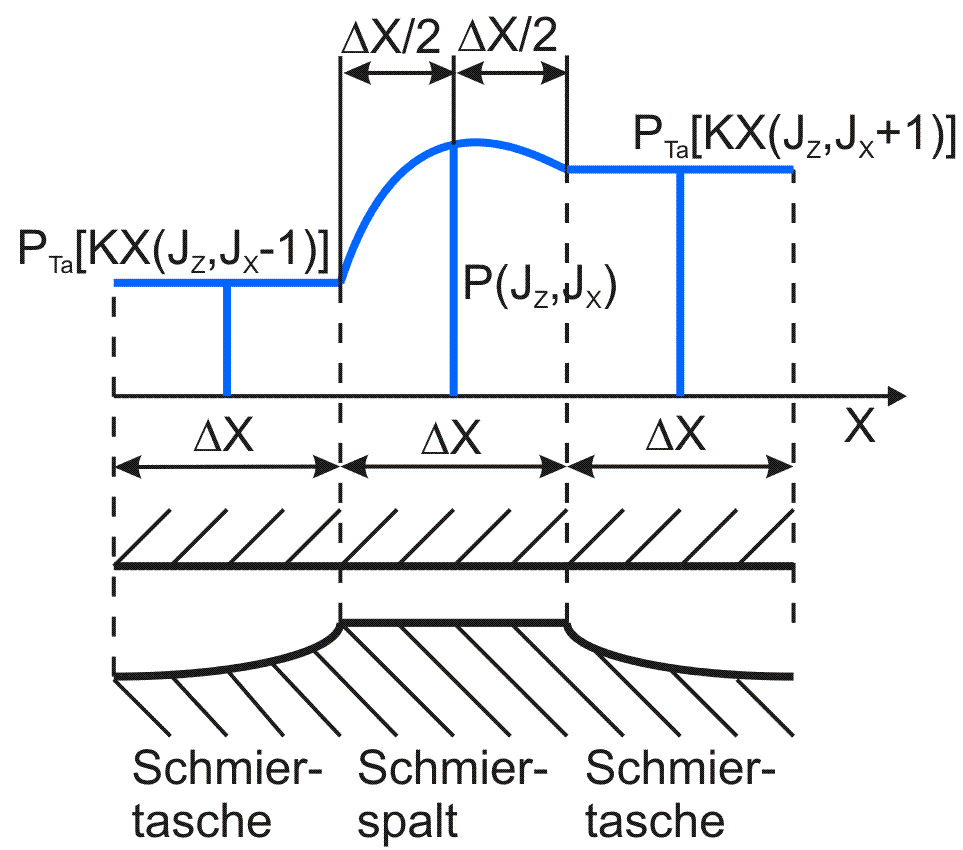 Bild 3.27: Skizze zu Variante 4 |
Für die partiellen Ableitungen in X-Richtung gilt

 Für den analogen Fall in Z-Richtung gilt 
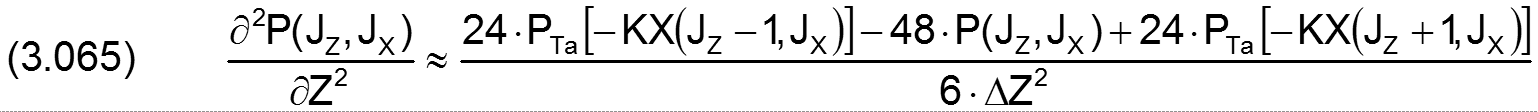 |
Variante 5: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in negativer Richtung der Koordinatenachse an den Rand des Lagers. Bild 3.28 skizziert diesen Fall für die X-Richtung.
 Bild 3.28: Skizze zu Variante 5 |
Für die partiellen Ableitungen in X-Richtung gilt

 Für den analogen Fall in Z-Richtung gilt 
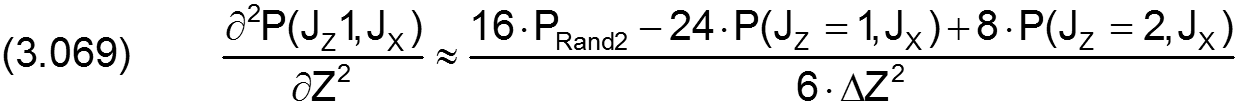 |
Variante 6: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in der negativen Richtung der entsprechenden Koordinatenachse an den Lagerrand und in positive Richtung an das Flächenelement einer Schmiertasche. Bild 3.29 skizziert diesen Fall für die X-Richtung.
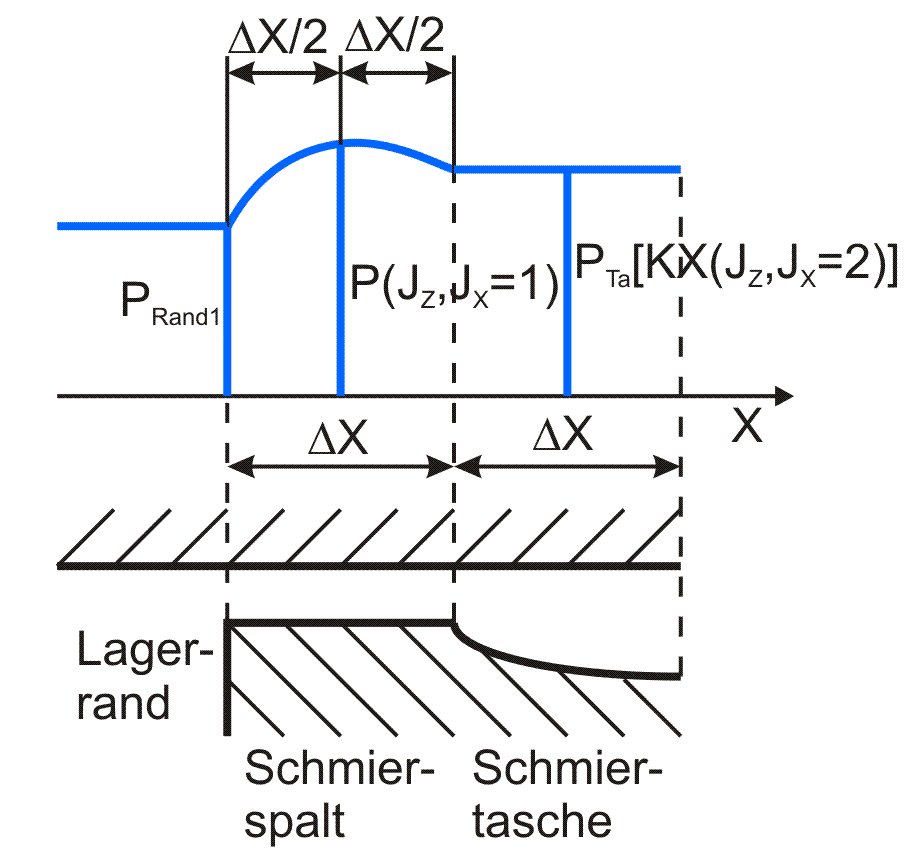 Bild 3.29: Skizze zu Variante 6 |
Für die partiellen Ableitungen in X-Richtung gilt

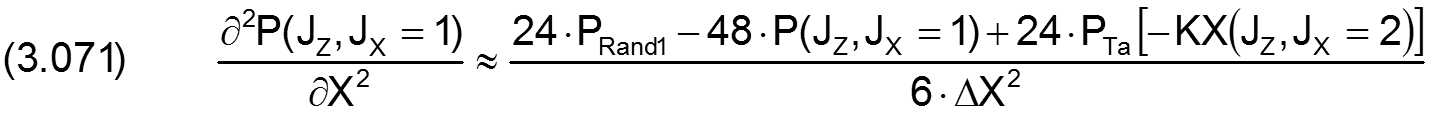 Für den analogen Fall in Z-Richtung gilt 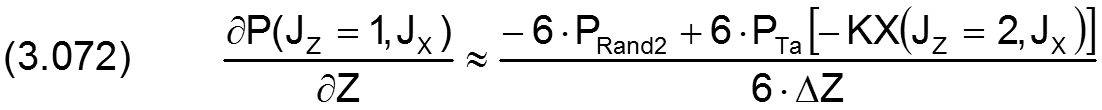
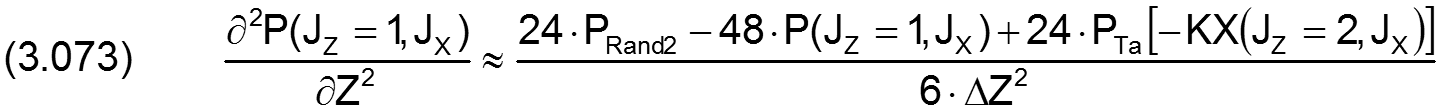 |
Variante 7: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in positiver Richtung der Koordinatenachse an den Lagerrand. Bild 3.30 skizziert diesen Fall für die X-Richtung.
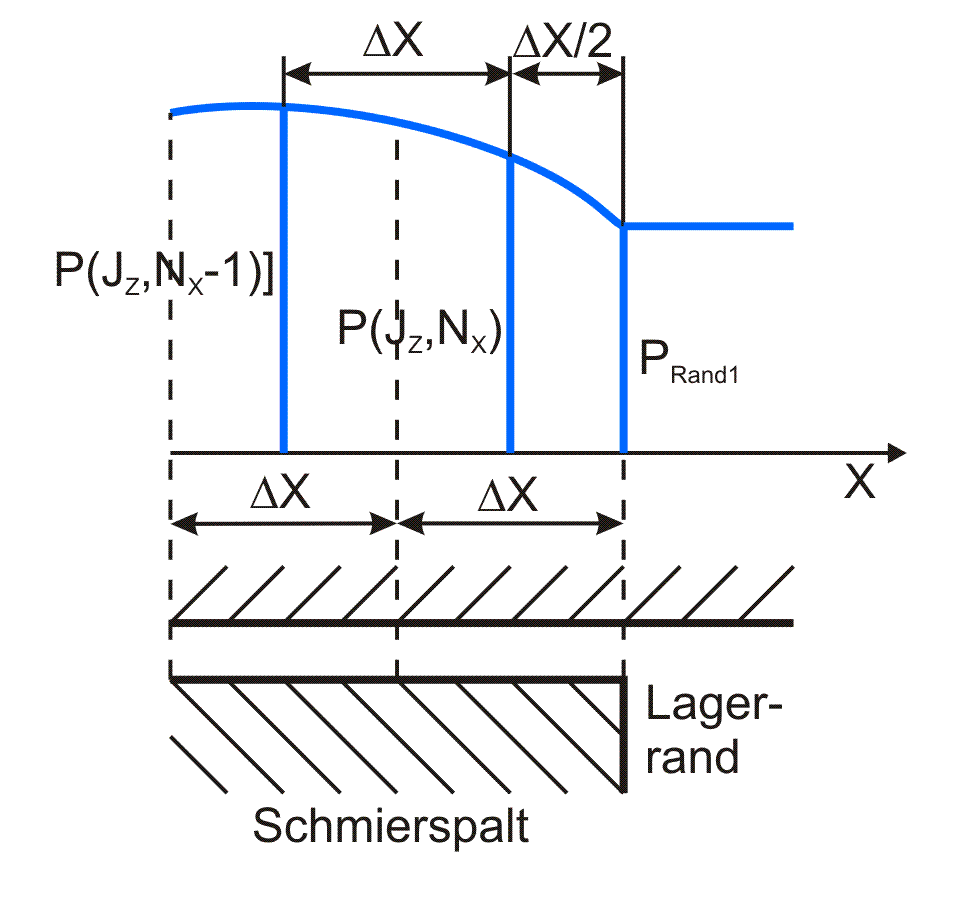 Bild 3.30: Skizze zu Variante 7 |
Für die partiellen Ableitungen in X-Richtung gilt
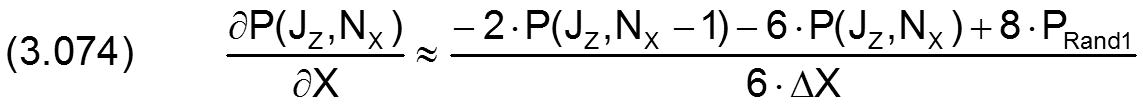
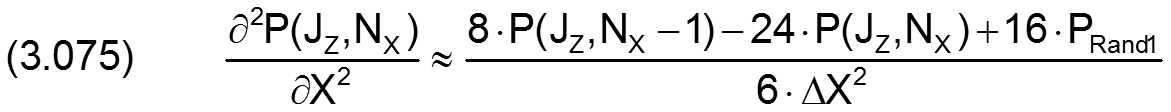 Für den analogen Fall in Z-Richtung gilt 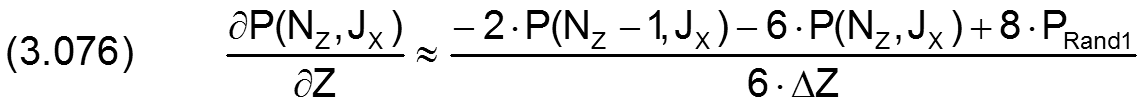
 |
Variante 8: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in negativer Richtung der entsprechenden Koordinatenachse an das Flächenelement einer Schmiertasche und in positiver Richtung an den Lagerrand. Bild 3.31 skizziert diesen Fall für die X-Richtung.
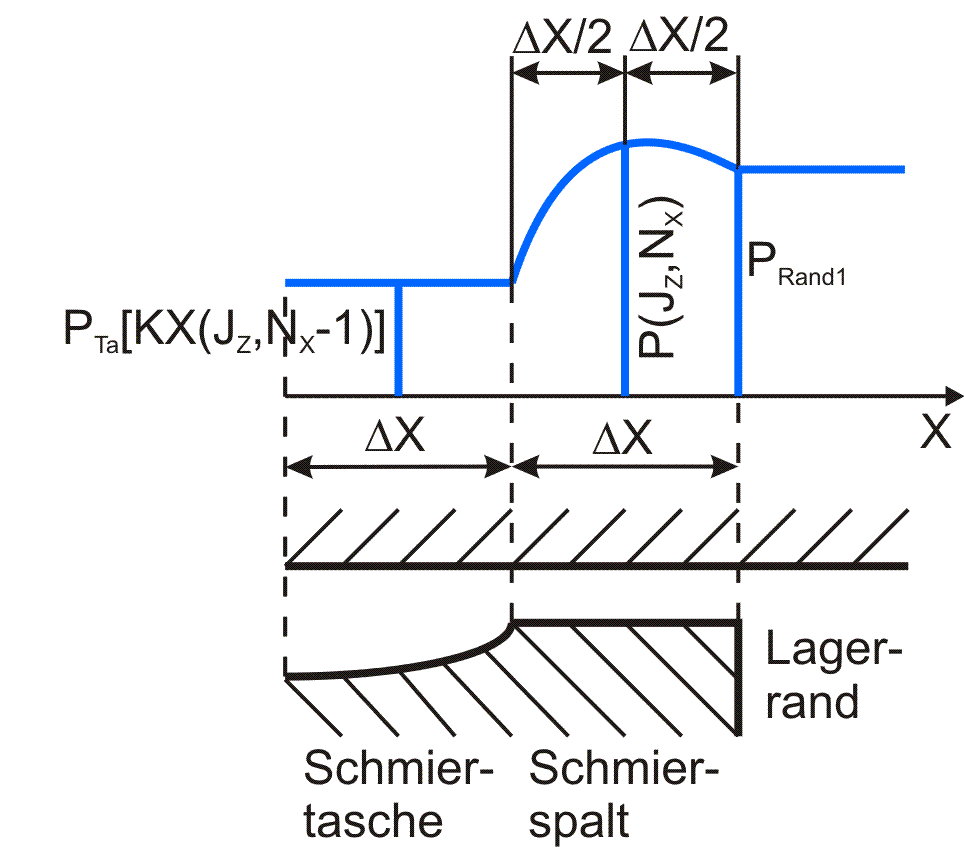 Bild 3.31: Skizze zu Variante 8 |
Für die partiellen Ableitungen in X-Richtung gilt
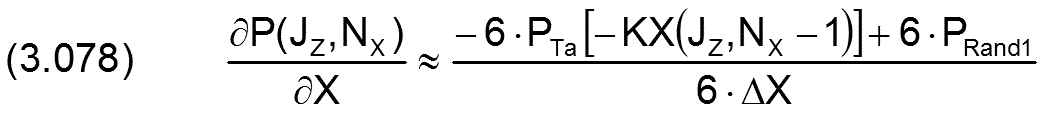
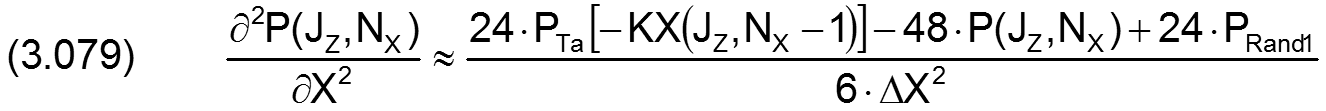 Für den analogen Fall in Z-Richtung gilt 
 |
Für die Berechnung der Differenzenquotienten ∂P/∂Z und ∂²P/∂Z² gibt es wegen der möglichen Symmetrie im Lager noch 2 weitere Varianten.
Variante 9: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in Richtung der negativen Z-Achse an die Symmetrieebene des Lagers und in Richtung der positiven Z-Achse an ein Flächenelement des eigentlichen Schmierspalts. Bild 3.32 skizziert diesen Fall für die Z-Richtung.
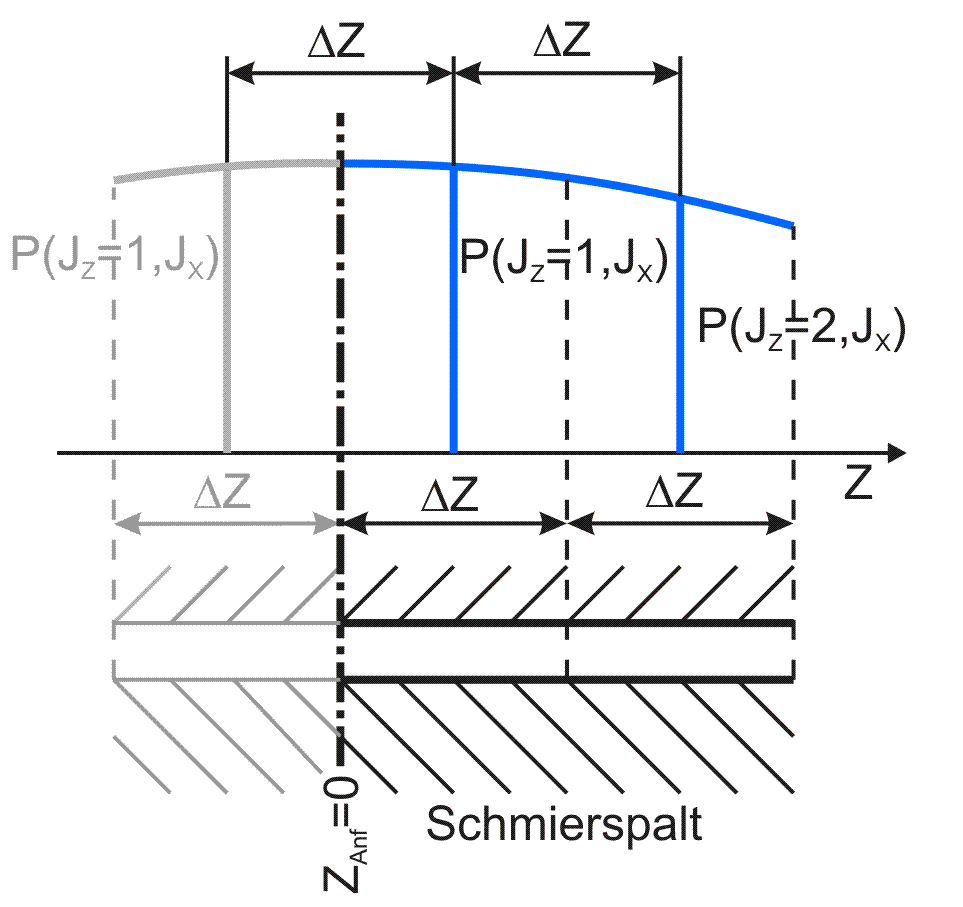 Bild 3.32: Skizze zu Variante 9 |
Für die partiellen Ableitungen in Z-Richtung gilt
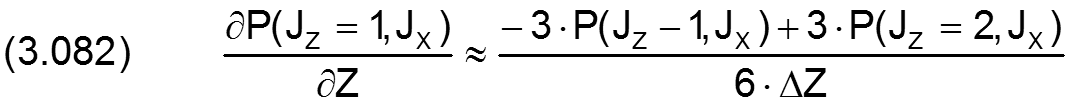
 |
Variante 10: Das Flächenelement (JZ,JX) des Schmierspalts grenzt in Richtung der negativen Z-Achse an die Symmetrieebene des Lagers und in Richtung der positiven Z-Achse an das Flächenelement einer Schmiertasche. Bild 3.33 skizziert diesen Fall für die Z-Richtung.
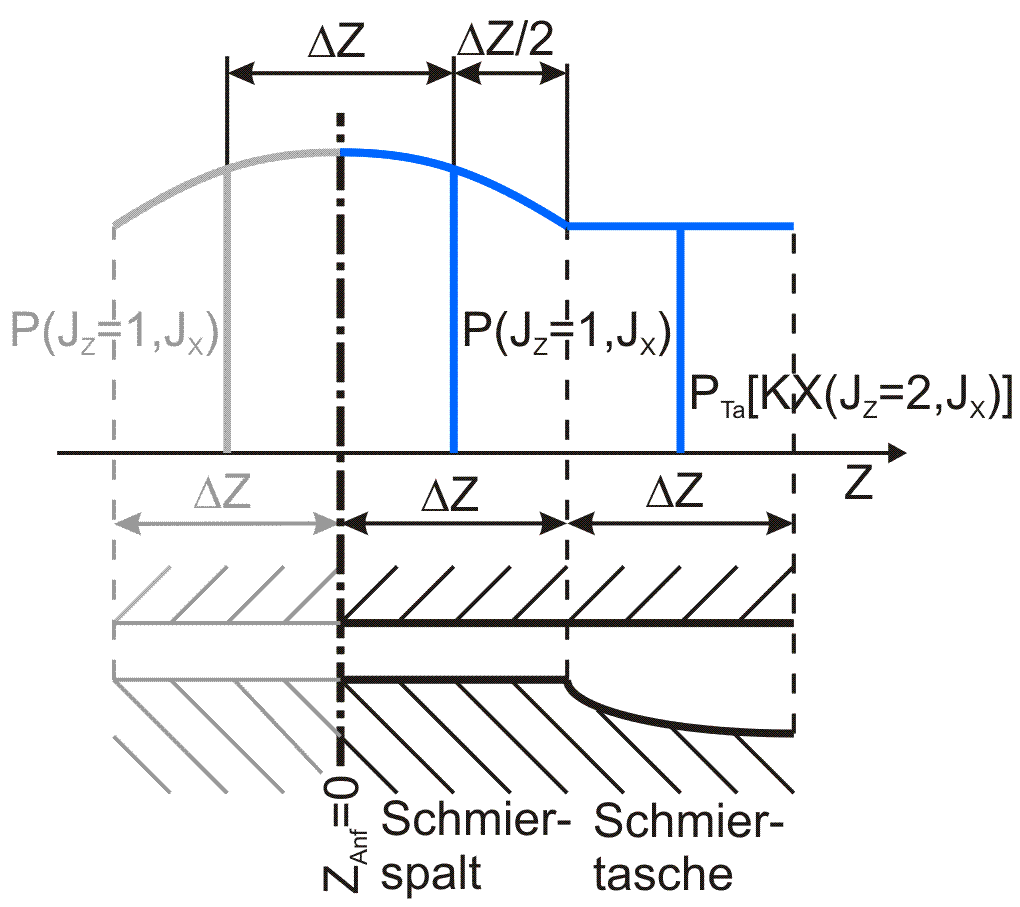 Bild 3.33: Skizze zu Variante 10 |
Für die partiellen Ableitungen in Z-Richtung gilt
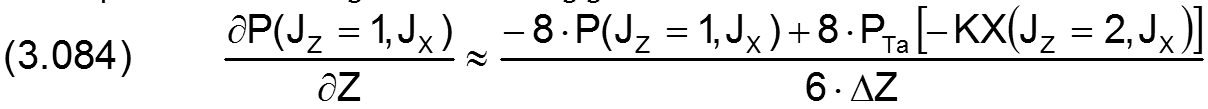
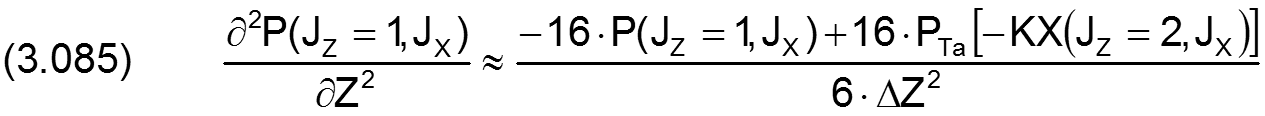 |
Welche Formeln auf welches Flächenelement angewendet werden müssen, wird durch positive ganzzahlige Werte in den Steuerfeldern KX und KZ codiert abgelegt. Im Steuerfeld KX werden programmintern neben der Anordnung der Schmiertaschen auch die Variantennummern der entsprechenden Differenzenformeln für die partiellen Ableitungen ∂P/∂X und ∂²P/∂X² abgelegt. Bild 3.34 zeigt die Steuerfelder KX für die 2 Lagervarianten analog zu Bild 3.23, wie sie programmintern mit diesen Variantennummern aufgefüllt wurden. Die Nummerierung der Varianten im Feld KX ist identisch mit der Nummerierung der Varianten 1 bis 8 hier in der Dokumentation.
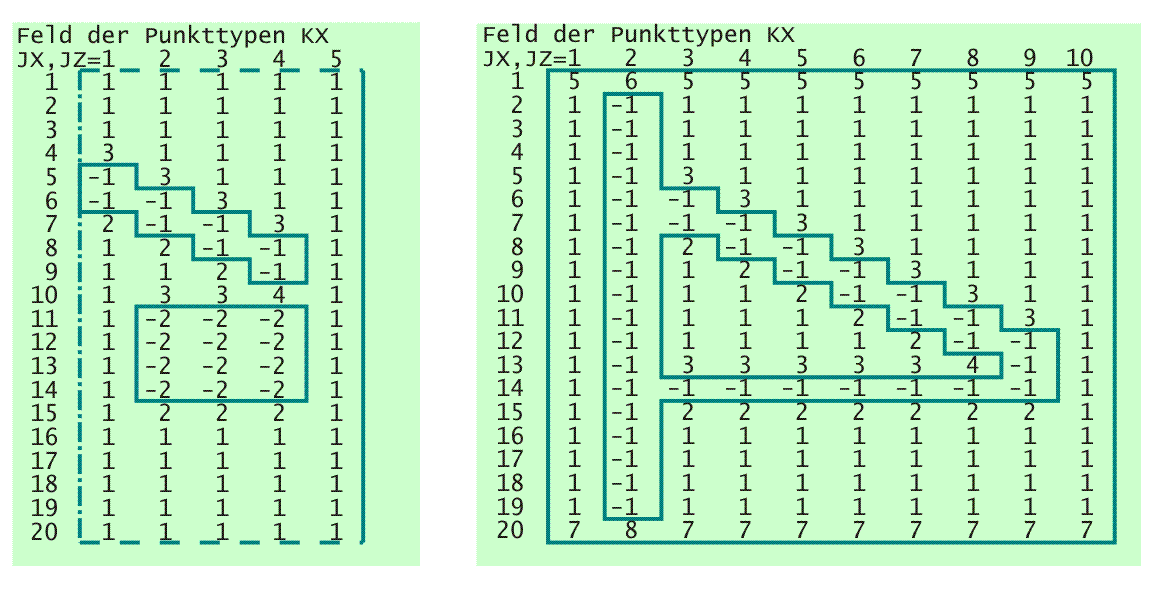
Bild 3.34: Darstellung der vollständigen Steuerfelder KX für die 2 Varianten von Schmiertaschenanordnungen analog zu Bild 3.23
Im Steuerfeld KZ werden die Variantennummern der entsprechenden Differenzenformeln für die partiellen Ableitungen ∂P/∂Z und ∂²P/∂Z² abgelegt. Bild 3.35 zeigt die Steuerfelder KZ für die 2 Lagervarianten mit den Schmiertaschenanordnungen des Bildes Bild 3.23. Die Nummerierung der Varianten im Feld KZ ist identisch mit der Nummerierung der Varianten 1 bis 10 hier in der Dokumentation.

Bild 3.35: Darstellung der Steuerfelder KZ für die 2 Varianten von Schmiertaschenanordnungen entsprechend Bild 3.23
Zusätzlich zu den beiden Steuerfeldern KX und KZ erzeugt das Programm ein 3.Steuerfeld NG der Größe NZ NX, in dem es den einzelnen Flächenelementen der Schmierspaltfläche die Gleichungsnummern zuordnet, mit denen sie innerhalb des zu erzeugenden Gleichungssystems aufgeführt werden. Bild 3.36 zeigt die Steuerfelder NG für die 2 Lagervarianten mit den Schmiertaschenanordnungen des Bildes Bild 3.23.

Bild 3.36: Darstellung der Steuerfelder NG für die 2 Varianten von Schmiertaschenanordnungen entsprechend Bild 3.23
Der Programmanwender bekommt das Steuerfeld KX nur in der Version des Bildes 3.23 zu sehen, ohne die internen Variantennummern für die Differenzenformeln, die die Darstellung an der Programmoberfläche nur unübersichtlicher machen würden. Die Steuerfelder KZ und NG bekommt er gar nicht zu Gesicht. Diese sind nur für den Programmierer bei einer Bearbeitung oder Weiterentwicklung des Programms von Interesse. Man kann sich diese Felder aber anzeigen lassen, wenn man in der Routine "PreProzessor" die Zeile
"c call Kondru(NX,NZ,KX,KZ,NG,NGL)"
aktiviert, indem man den Buchstaben "c" am Zeilenanfang des Quelltexts entfernt und anschließend den Quelltext neu kompiliert. Nach dem Neustart des Programms werden dann die Steuerfelder KX, KZ und NG vollständig angezeigt, wenn im PreProzessor das Hauptmenü "Anordnung der Schmiertaschen festlegen" verlassen wird.
Die Vervollständigung des Steuerfeldes KX mit den Variantennummern und die Erzeugung der Steuerfelder KZ und NG erledigt die Routine "Muster", so dass diese Daten für eine zügige Berechnung der Koeffizientenmatrix des Gleichungssystems während der Hauptrechnung zur Verfügung stehen.
zurück weiterDurch die 8 Varianten für die Ableitungen in X-Richtung und die 10 Varianten für die Ableitungen in Z-Richtung gibt es 80 verschiedene Varianten von Differenzengleichungen zur Berechnung der Druckverteilung im Schmierspalt. Mit Hilfe der Steuerfelder KX, KZ und NG kann für jedes Feldelement des Schmierspalts die richtige lineare Differenzengleichung aufgestellt werden.
Nachfolgend soll als Beispiel eine Variante der aufzustellenden Differenzengleichungen gezeigt werden:
Ausgangsgleichung ist die lineare bzw. linearisierte Differentialgleichung der Form
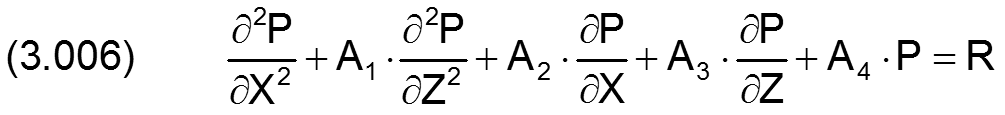
Für den häufigsten Fall, nämlich für die Variante mit KX(JZ,JX)=1 und KZ(JZ,JX)=1, lautet die Differenzengleichung, die die Differentialgleichung approximiert,
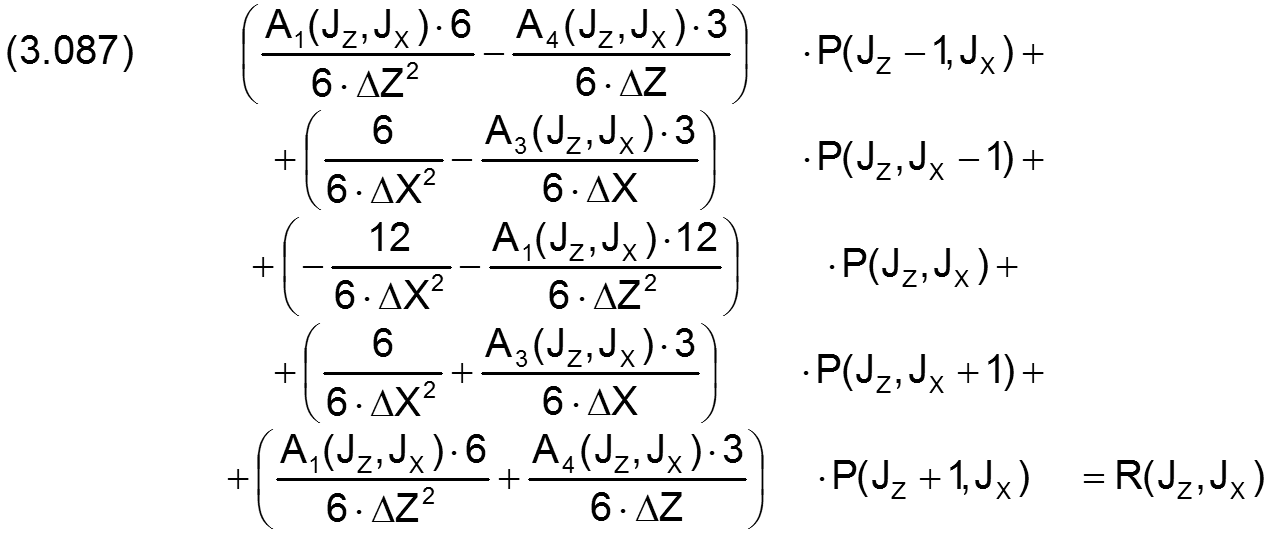
Wenn die zu berechnende Lagervariante ausnahmsweise mal keine Schmiertaschen besitzt, dann wird das lineare Gleichungssystem zur Berechnung der Druckverteilung P(NZ,NX) ausschließlich aus NX·NZ=NGlei=NGlei1 Gleichungen gebildet, die die lineare bzw. linearisierte Differentialgleichung approximieren. Die Routine "KoMa1" erzeugt dazu die ungepackte Matrix K(NGlei1,NGlei1) und den Vektor der rechten Seiten R(NGlei1), womit das Gleichungssystem vollständig beschrieben ist und durch ein nummerisches Lösungsverfahren z.B. einen Gauss-Algorithmus mit Pivotisierung durch Routine "SIMQ" gelöst werden kann. Die Routine "KoMa1_pack" erzeugt analog dazu die Felder Kv, Kc und Kp und den Parameter M, die gemeinsam die entsprechende gepackte Matrix zur ungepackten Matrix K darstellen. Standardmäßig werden die gepackten Matrizen verwendet und mit dem GMRES-Verfahren mit ILU-Konditionierung gelöst, weil dieses wesentlich schneller arbeitet. Die Verwendung der ungepackten Matrizen und ihre Lösung mit einem Gauss-Algorithmus werden nur noch zur Kontrolle verwendet im Rahmen der Entwicklung und Fehlersuche. Ausführlicher dazu siehe Abschnitt 3.4.5.
Üblicherweise sind Gleitlager mit Schmiertaschen bzw. Schmiernuten versehen, über die Schmiermittel zu- bzw. auch abgeleitet werden kann. Diese sind dann über Verbindungsleitungen mit einer oder mehreren Schmiermittelpumpen verbunden. Schmiertaschen belegen einen Teil der Spaltfläche des Lagers zwischen Welle und Lagerschale. Da hier die Spalthöhe wesentlich größer ist als im eigentlichen Schmierspalt, kann hier die Newtonsche Reibung in der Flüssigkeit vernachlässigt werden und es gilt nicht die Reynoldssche Gleichung. Dieser Raum kann als ein reibungsverlustfreier hydrostatischer Raum aufgefasst werden, für den "lediglich" eine Volumenbilanz der durchströmenden Schmierflüssigkeit aufgestellt werden muss.
Auch in den Schmiertaschen ist der Schmiermitteldruck zunächst unbekannt und muss im Rahmen der Hauptrechnung mit berechnet werden. Dazu ist die Bilanz des Flüssigkeitsvolumens jeder Schmiertasche aufzustellen. Die Gleichung (2.676) gibt die dimensionslose Bilanz des Flüssigkeitsvolumens einer Schmiertasche an.

Dabei sind QTa der Schmiermittelstrom aus den angeschlossenen Verbindungleitungen in die Schmiertasche JTa, QTaRand der Schmiermittelstrom über den Schmiertaschenrand in den Schmierspalt, gemäß Gleichung (2.667), und ∂VolFlTa/∂T die Änderung des Flüssigkeitsvolumens in der Schmiertasche, gemäß Gleichung (2.674). Die Parameter QTaRand und ∂VolFlTa/∂T resultieren aus einer Integration über den Taschenrand bzw. über die Taschenfläche. Um diese Gleichungen in das zu berechnende lineare Gleichungssystem intergieren zu können, sind diese Integrale durch geeignete lineare Summenformeln zu approximieren. Dazu kann die bereits eingeführte Diskretisierung der Spaltfläche in NX·NZ Flächenelemente genutzt werden.
Zunächst soll das an einer Schmiertasche erläutert werden, die aus nur einem Flächenelement (JZ,JX) besteht.
zurück weiterBetrachten wir zunächst eine Schmiertasche, die nur aus dem Flächenelement ΔX·ΔZ besteht an der Stelle (JZ,JX). In Bild 3.37 sind die diskretisierten Schmiermittelströme und der Druckverlauf P in der Umgebung des Elements skizziert.
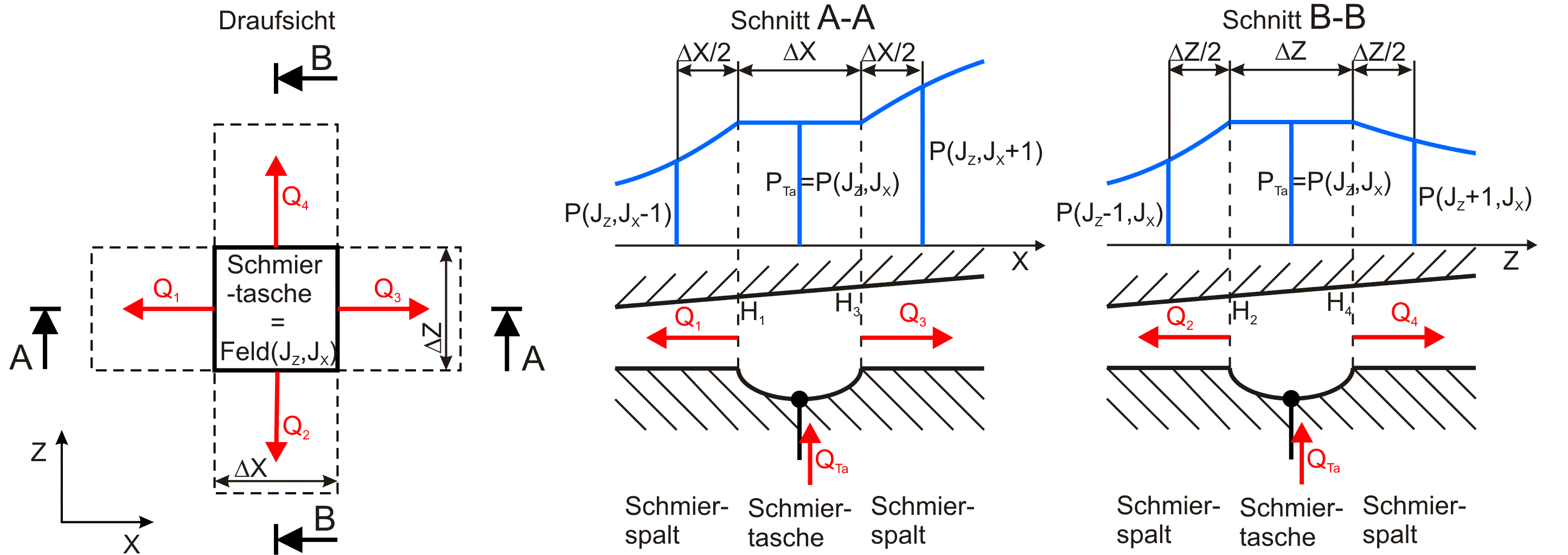
Bild 3.37: Skizzen zu den Schmiermittelströmen über den Rand einer Schmiertasche, die nur aus einem Flächenelement besteht
Der Schmiermittelstrom QTaRand über den Rand der Schmiertasche ist gemäß Gleichung (2.667) das Ringintegral über den Schmiertaschenrand.
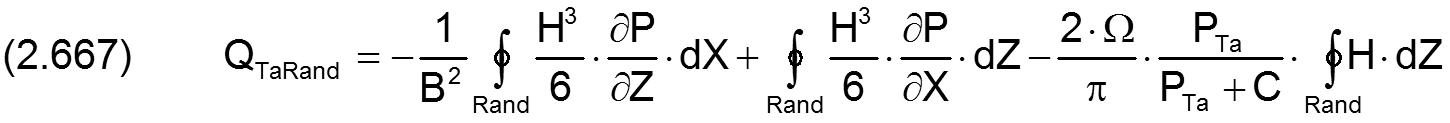
Er lässt sich für ein Flächenelement ΔX·ΔZ approximieren durch die Summe der 4 Teilströme.
![]()
Für die Teilströme lassen sich jetzt analog Gleichung (2.667) die Näherungsgleichungen angeben.
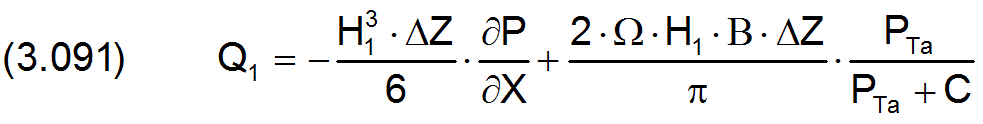
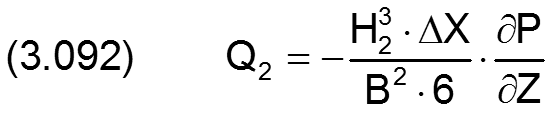
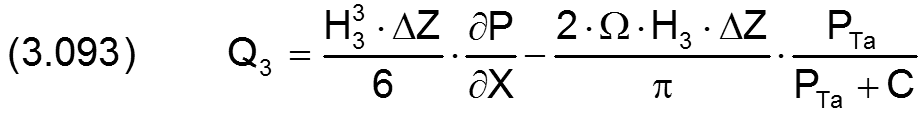

Die partiellen Ableitungen des Drucks in den 4 Formeln sind jeweils die Druckanstiege direkt am jeweiligen Schmiermittelrand. Sie können näherungsweise angegeben werden durch die 4 Formeln
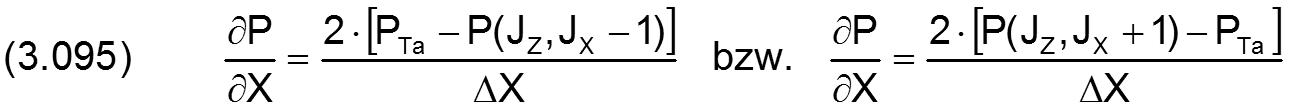
und
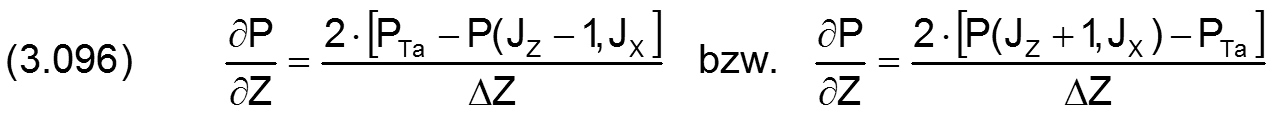
In den Gleichungen (3.091) und (3.093) befindet sich noch ein nichtlinearer Ausdruck PTa/(PTa+C). Analog zu den Linearisierungen der erweiterten Reynoldsschen Differentialgleichung wird dieser ersetzt durch folgenden linearen Ausdruck:

Nun können alle 4 Teilströme durch lineare Näherungsformeln geschrieben werden.
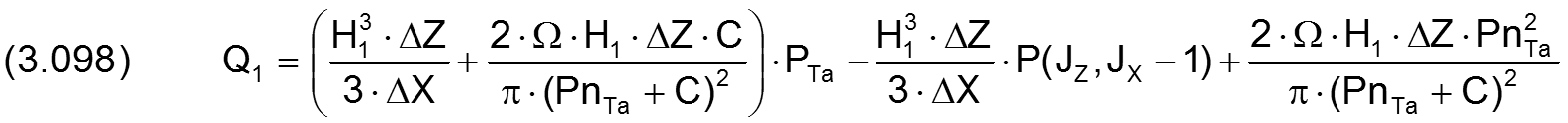
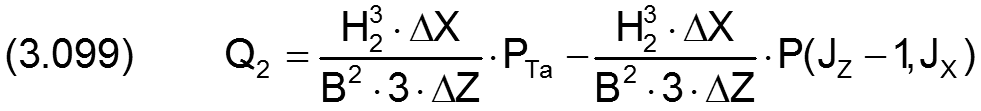
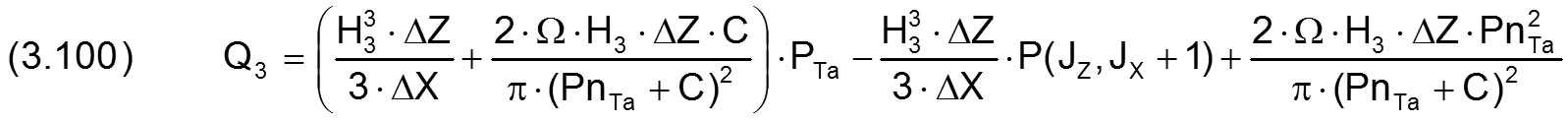
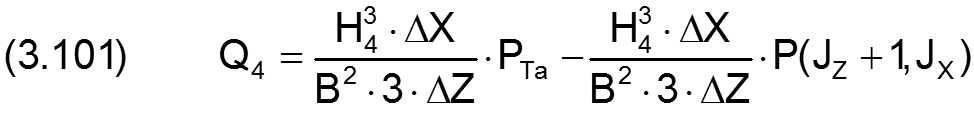
Mit den 4 Gleichungen (3.098) bis (3.101) kann man jetzt den Schmiermittelstrom QTaRand über den Schmiertaschenrand als lineare Gleichung schreiben mit den 6 Unbekannten P(JZ-1,JX), P(JZ,JX-1), P(JZ,JX+1), P(JZ+1,JX), PTa und QTaRand in folgender Form.
![]()
Die Koeffizienten der Gleichung werden hier nicht ausgeschrieben, da diese Formel zu umfangreich und unübersichtlich wird. Sie wurde in dieser Form auch nie ausgeschrieben. Im Programm werden diese Koeffizienten rekursiv über mehrere Hilfsvariable wesentlich rationeller bestimmt.
Durch eine Änderung der Spalthöhe ∂H(JZ,JX)/∂T und/oder eine Druckänderung ∂PTa/∂T kann sich das Flüssigkeitsvolumens VolFlTa in der Schmiertasche ändern, was in die Volumenbilanz des Schmiertaschenelements eingehen muss.
In Anlehnung an die Gleichung (2.674) ist die dimensionslose Änderung des Flüssigkeitsvolumens in einem Schmiertaschenelement über die Zeit T näherungsweise gegeben durch

In der Hauptrechnung soll zunächst der Druck in der Schmiertasche berechnet werden. Deshalb ist die Gleichung (3.103) auf die Angabe von Druck umzustellen. Der örtliche Füllungsgrad FTa des Schmierspalts ist gegeben durch den Druck PTa in der Schmiertasche gemäß Gleichung (2.614).
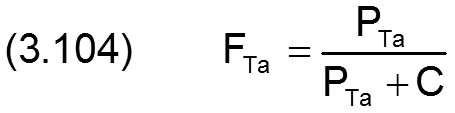
Die Ableitung nach der Zeit T ist dann gegeben durch
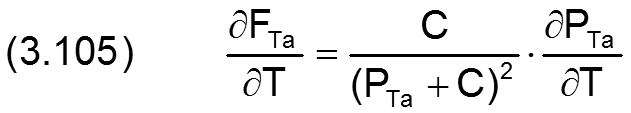
Würde man die Gleichungen (3.104) und (3.105) in die Gleichung (3.102) einsetzen, würde diese wieder nichtlinear, was nicht im Sinne des Lösungsverfahrens ist, nämlich ein lineares Gleichungssystem zu erzeugen. Deshalb werden auch diese Gleichungen zunächst wieder in gewohnter Weise durch linearisierte Näherungen ersetzt.
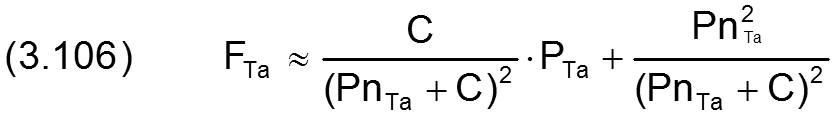
und

Dabei wird die Ableitung von PnTa über die Zeit näherungsweise berechnet durch die Gleichung
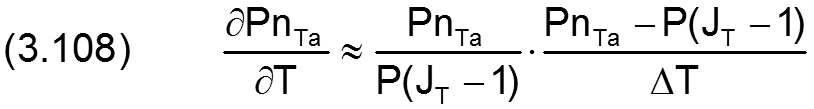
PnTa ist hier die vorhergehende Näherung für den Druck PTa für den aktuellen Zeitpunkt JT. PTa(JT-1) ist der Schmiertaschendruck zum vorhergehenden Zeitpunkt. Ausführlich erläutert ist die Linearisierung in [20, Abschnitt 7.3].
Damit lässt sich auch die Änderung des Schmierflüssigkeitsvolumens in der Schmiertasche durch einen linearen Ausdruck angeben in der Form

Die Koeffizienten der Gleichung werden auch hier nicht ausgeschrieben, da diese Formel zu umfangreich und unübersichtlich wird. Sie wurde in dieser Form auch nie ausgeschrieben. Im Programm werden diese Koeffizienten rekursiv über mehrere Hilfsvariable wesentlich rationeller bestimmt.
Mit den Formeln der beiden vorhergehenden Abschnitte lässt sich jetzt die Volumenbilanz der Schmiermittelströme in einem Flächenelement einer Schmiertasche angeben als lineare Gleichung in der Form
![]()
Bild 3.38 zeigt anhand der Steuermatrix KX die Ausdehnung der ersten Schmiertasche JTa=1 über mehrere Flächenelemente ΔX·ΔZ.
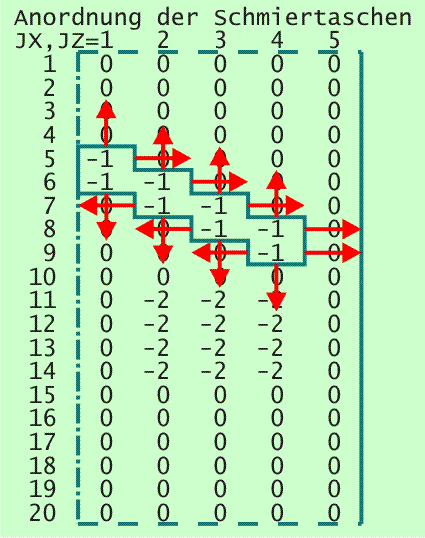
Bild 3.38: Diskretisierte Schmiermittelströme über den Rand einer Schmiertasche
Die roten Pfeile sollen die diskretisierten Teilölströme aus der Schmiertasche in den eigentlichen Schmierspalt darstellen. Rechnerisch wäre es korrekt, wenn man sich eine großflächige Schmiertasche aus mehreren elementaren Schmiertaschen, bestehend aus je einem Flächenelement, vorstellt und die Volumenbilanzen der Teilflächen gemäß Formel (3.109) aufsummiert. Die internen Schmiermittelströme über die Elementgrenzen würden sich dann gegenseitig aufheben.
Programmintern werden aber nur die erforderlichen Ströme am Taschenrand berechnet. Hier bedient sich das Programm wieder der Steuermatrix KX, indem es abfragt, ob neben dem aktuell behandelten Flächenelement auch noch Flächenelemente von Schmiertaschen oder der Lagerrand liegen.
So ist für jede der NTa Schmiertaschen genau eine weitere lineare Gleichung in das Gleichungssystem der Hauptrechnung zu schreiben.
Die Routine "KoMa3" bzw. die Routine "KoMa3_pack" erledigt das. Dabei kommen die Drücke PTa(JTa) mit JTa=1 bis NTa als weitere Unbekannte in das Gleichungssystem. Der Ölstrom QTa erscheint nicht explizit als eine Unbekannte im Gleichungssystem. An ihrer Stelle werden der bzw. die entsprechenden Ölströme QVe(JVe) aus den Verbindungsleitungen eingetragen, mit denen die jeweilige Schmiertasche verbunden ist.
zurück weiterDas periphere Schmiermittel-Versorgungssystem kann mehrere Schmiermittelpumpen besitzen, die durch mehrere Verbindungsleitungen auf sehr unterschiedliche Weise mit den einzelnen Schmiertaschen verbunden sind. In diesen Leitungen ist jeweils ein Gerät angeordnet, dass den Schmiermittelstrom durch die Leitung beeinflusst. Im Rahmen der Hauptrechnung zum Lager müssen simultan zur Berechnung der Druckverteilung im Schmierspalt diverse Drücke und Schmiermittelströme als primäre Ergebnisparameter berechnet werden. Die notwendigen Ergebnisparameter für das Schmiersystem, aus denen dann auch alle anderen Daten ermittelt werden können, sind neben den Schmiertaschendrücken PTa die aktuellen Schmiermittelströme QVe durch die einzelnen Verbindungsleitungen, die Pumpenströme QPu und die Pumpendrücke PPu. Dazu sind die Gerätekennlinien und die Verknüpfungen der Elemente des Schmiersystems durch geeignete lineare Gleichungen abzubilden, die dem linearen Gleichungssystem zugefügt werden.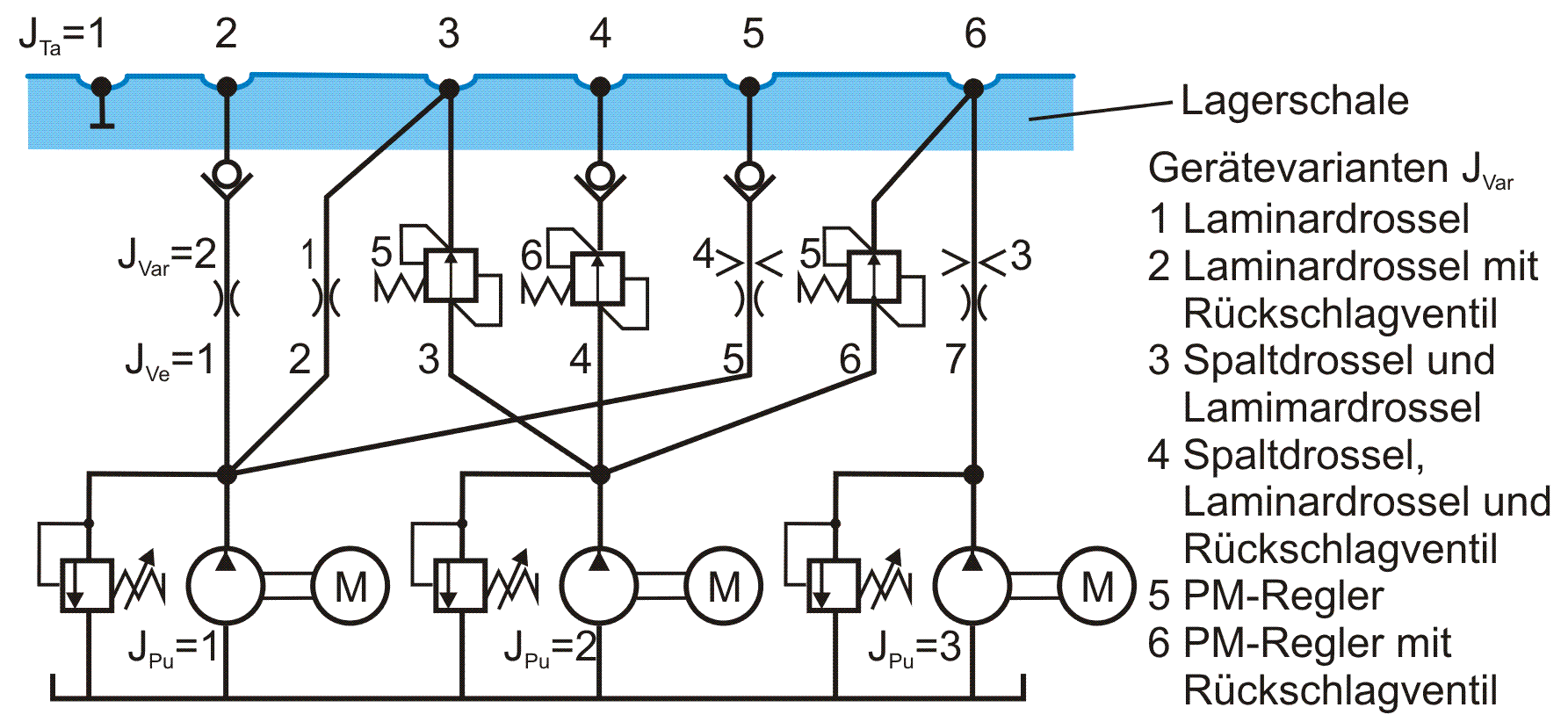
Bild 4.025: x
Bild 4.025 zeigt beispielhaft die mögliche Komplexität eines solchen Schmiermittel-Versorgungssystems. Bis auf die nichtlineare Kennlinie der Spaltdrossel sind die Gerätekennlinien recht einfache lineare Funktionen. Allerdings bestehen diese teilweise aus mehreren Ästen, aus denen sie zusammengesetzt sind. Die eigentliche Herausforderung der Programmierung des Schmiermittel-Versorgungssystems ist die Abbildung der Verknüpfungen der verschiedenen Elemente. So muss das Programm befähigt werden, anhand der verfügbaren Steuerparameter für jeden konkreten Fall automatisch die richtigen Gleichungen auszuwählen und dementsprechend die Koeffizienten in die Matrix des Gleichungssystems einzutragen. Erschwert wird diese Aufgabe weiter dadurch, dass anschließend ein schnelles Lösungsverfahren verwendet werden soll, dass mit einer gepackten Matrix arbeitet (siehe Abschnitt 3.4.5.1). Die gepackte Matrix macht das Ganze noch unübersichtlicher. Der Aufwand lohnt sich aber, da mit diesem Verfahren gegenüber dem Verfahren mit ungepackter Matrix eine Verkürzung der Rechenzeit um den Faktor 1000 erreicht wird.
Die Lösung dieser Teilaufgabe ist in der Routine KoMa4 bzw. KoMa4_pack realisiert. Die Erzeugung dieser Routinen war für den Autor eine der schwierigsten Teilaufgaben, weil es hier besonders schwierig ist, den Überblick über die vielen verschiedenen logischen Verknüpfungen zu behalten. Beruhigend an der Programmierung dieses Teilsystems ist, dass die Überprüfung der Ergebnisse auf ihre Richtigkeit recht einfach ist, weil man mit einfachen Gleichungen das Ergebnis manuell nachrechnen kann. Wenn allerdings ein Fehler festgestellt wird, ist die Fehlersuche recht aufwendig.
Das mag den Anwender nicht weiter interessieren, wenn einmal das Programm erzeugt und ausführlich getestet wurde. Da der Autor das Programm aber nicht nur als Black Box zur allgemeinen Nutzung übergeben möchte, sondern es auch zulässt und dazu anregen möchte, das Programm zu ergänzen und weiterzuentwickeln, soll hier die Programmierung in möglichst verständlicher Form offengelegt werden. Zur Lösung des Problems ist der Autor in 3 Schritten vorgegangen:
1. Es wurde der Programmablauf in einer programmähnlichen und noch recht gut lesbaren Schreibweise entworfen. Siehe Abschnitt 3.4.3.2.
2. Die Routine KoMa4 wurde zunächst für den einfacheren Fall, mit ungepackter Koeffizientenmatrix, geschrieben und getestet.
3. Mit der Routine KoMa4_pack wurde die Routine aus Koma4 umgeschrieben für den unübersichtlicheren Fall mit einer gepackten Matrix.
Nachdem das Problem erfolgreich mit gepackter Matrix gelöst war, wurde die Routine KoMa4 und ihre Einbindung in die übergeordneten Routinen nicht etwa entfernt, sondern sie wurde nur innerhalb des Programms deaktiviert. Im Falle eines auftretenden Fehlers oder zur Weiterentwicklung des Programms kann diese Routine leicht wieder aktiviert werden. Siehe dazu Abschnitt 3.4.5.4.
zurück weiterDie Betriebskennlinie einer Spaltdrossel (Blende) in Reihe mit einer Laminardrossel (Kapillare) ohne Rückschlagventil wird durch die 2 Gleichungen abgebildet (siehe dazu auch den Abschnitt 2.2.6.2.2)
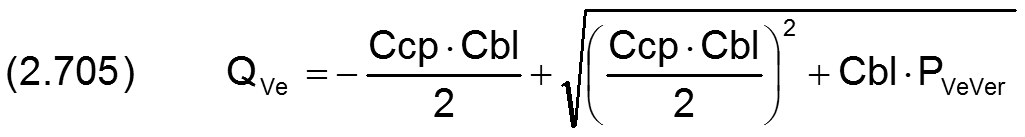 |
für PVeVer ≥ 0 |
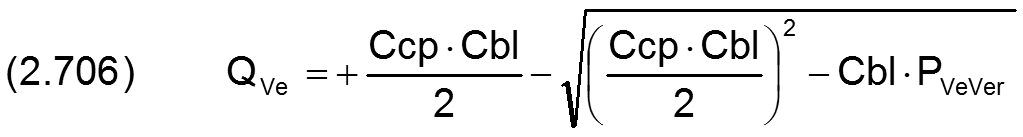 |
für PVeVer<0 |
| Ccp | dimensionsloser Widerstandsbeiwert des laminaren Strömungswiderstandes |
| Cbl | dimensionsloser Blendenbeiwert der Spaltdrossel |
| PVeVer | dimensionsloser Druckverlust über die Drosseln PVeVer=PPu-PTa |
Das ist bisher die einzige Kennlinie der implementierten, stromregelnden Geräte in den Verbindungsleitungen, die nicht linear ist. Um diese Kennlinie in das lineare Gleichungssystem der Hauptrechnung einbeziehen zu können, muss auch diese Gleichung analog zur Linearisierung der erweiterten Reynoldsschen Gleichung linearisiert werden und kann so ebenfalls iterativ berechnet werden. Das bietet sich an, da in der Berechnung ohnehin bereits mehrere Iterationszyklen existieren, in denen auch diese Iteration erfolgen kann, so dass das keinen nennenswerten zusätzlichen Rechenaufwand bedeutet.
Auch hier wird für die Linearisierung ein Ansatz mit den ersten 2 Gliedern der Taylorreihe verwendet
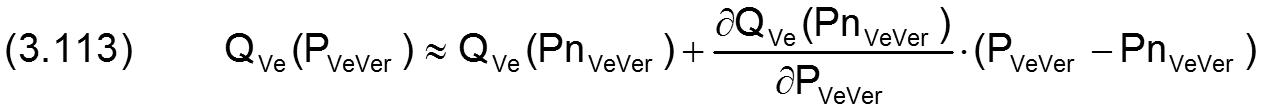
Angewendet auf die beiden Gleichungen (2.705) und (2.706) ergibt das die Gleichungen
![]()
und
![]()
mit
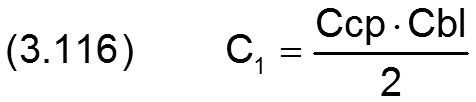
![]()
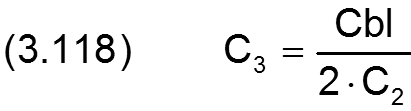
Mit der Definition der Funktion sign(x,y), wie sie in der Programmiersprache FORTRAN definiert ist, lassen sich die beiden Gleichungen (3.114) und (3.115) zusammenfassen.
![]()
Für den Fall, dass die Schmiermittelpumpe aktuell als Pumpe mit konstantem Pumpendruck arbeitet (druckgeregelte Pumpe), d.h. PnPu=PPu=PPuMax, gilt
![]()
und
![]()
Eingesetzt in die Gleichung (3.119) ergibt das die linearisierte Gleichung für die Kennlinie
![]()
Für den Fall, dass die Schmiermittelpumpe aktuell als Pumpe mit konstantem Förderstrom arbeitet (Konstantpumpe), d.h. PnPu<PPuMax, gilt
![]()
und
![]()
Eingesetzt in die Gleichung (3.119) ergibt das die linearisierte Gleichung für die Kennlinie
![]()
Nachfolgend soll der Ablauf der Erzeugung der restlichen Gleichungen zur Abbildung des Schmiermittel-Versorgungssystems in einer programmähnlichen Form dargestellt werden. Es sind hier die eigentlichen Befehle in farbiger Schrift dargestellt, während die Kommentierung in der üblichen schwarzen Schrift erfolgt. Bei der Darstellung wurde zur Wahrung der Übersichtlichkeit weitgehend auf die Indizes zu den variablen Feldbezeichnungen verzichtet. Es wurde aber bereits die Reihenfolge der späteren Abarbeitung der Befehle in der Routine KoMa4 eingehalten.
Darstellung des Programmablaufs in KoMa4 in vereinfachter, lesbarer Form:
| J2 = NGlei + NTa | |
| J3 = NGlei + NTa + NVe | = J2 + NTa |
| J4 = NGlei + NTa + NVe + NPu | = J3 + NPu |
Ergänzen der NVe Gleichungen Nr. J2+1 bis J2+NVe, die den Zusammenhang zwischen dem Schmiermittelstrom QVe und dem Druckgefälle PVeVer = PPu - PTa in den NVe Verbindungsleitungen beschreiben. Das sind die Betriebskennlinien der jeweiligen Geräte in den Verbindungsleitungen: QVe=f(PVeVer=PPu-PTa) bzw. QVe=f(PVeVer=PPuMax-PTa)
Für JVe = 1 bis NVe tue folgendes:
Rechter horizontaler Ast der Kennlinie für alle Geräte mit Rückschlagventil
Wenn PnPu < PnTa und ein Rückschlagventil vorhanden ist, dann gilt:
QVe = 0
Gehe weiter zu Marke 20
endif.
Wenn das Gerät in der Leitung eine Kapillare ist, dann gilt:
| Wenn PuVar = 2, dann gilt | (Druckgeregelte Pumpe) |
| QVe = ( PPuMax -PTa ) / Ccp | (Gleichung 2.695) |
| Gehe weiter zu Marke 20 | |
| sonst gilt | (Konstantpumpe) |
| QVe = ( PPu - PTa ) / Ccp | (Gleichung 2.695) |
| Gehe weiter zu Marke 20 | |
| endif | |
| endif |
Wenn das Gerät in der Leitung ein PM-Regler ist, dann gilt:
| P0 = QP1 / Cpm | |
| Wenn PnTa </= PnPu - P0, dann gilt | (linker horizontaler Ast der Kennlinie) |
| QVe = 0 | (Gleichung 2.723, 1.Fall) |
| Gehe weiter zu Marke 20 | |
| endif | |
| Wenn ( PPu - P0 ) < PTa < ( PPu - PS ) , dann: | (aufsteigender Ast der Kennlinie) |
| Wenn PuVar = 2, dann gilt | (Druckgeregelte Pumpe) |
| QVe = QP1 - Cpm (PPuMax - PTa) | (Gleichung 2.723, 2.Fall) |
| sonst gilt | (Konstantpumpe) |
| QVe = QP1 - Cpm (PPu - PTa) | (Gleichung 2.723, 2.Fall) |
| endif | |
| Gehe weiter zu Marke 20 | |
| endif | |
| Wenn PnTa ≥ ( PPu - PS ), dann gilt: | (absteigender Ast der Kennlinie) |
| Wenn PuVar = 2, dann gilt | (Druckgeregelte Pumpe) |
| QVe = (PPuMax - PTa) / Rpm | (Gleichung 2.723, 3.Fall) |
| sonst gilt | (Konstantpumpe) |
| QVe = (PPu - PTa) / Rpm | (Gleichung 2.723, 3.Fall) |
| endif | |
| Gehe weiter zu Marke 20 | |
| endif | |
| endif |
Wenn das Gerät in der Leitung eine Blende und eine Kapillare in Reihe ist, dann gilt:
| C1 = Ccp Cbl / 2 | ||
| C2 = sqrt ( C1² + Cbl |PnPu - PnTa | ) | ||
| C3 = Cbl / 2 / C2 | ||
| Wenn PuVar = 2 , | ||
| dann gilt | (Druckgeregelte Pumpe) | |
| QVe = sign ( -C1+C2 , PnPu-PnTa ) + C3 PnTa - C3 PTa | (Gleichung 3.122) | |
| sonst gilt | (Konstantpumpe) | |
| QVe = sign ( -C1+C2 , PnPu-PnTa ) - C3 (PnPu - PnTa) + C3 PPu - C3 PTa | (Gleichung 3.125) | |
| endif | ||
| endif | ||
| Marke 20 |
Ende der Do-Schleife.
Ergänzen der NPu Gleichungen Nr. J3+1 bis J3+NPu für die aktuellen Schmiermittelströme QPu(JPu) der Pumpen:
| Für JPu = 1 bis NPu tue folgendes: | |
| Wenn PuVar = 1 , dann | (Konstantpumpe) |
| QPu = QPuMax | |
| Wenn PuVar = 2 , dann | (Druckgeregelte Pumpe) |
| QPu (JPu) = Summe (QVe ( JVe )) aller Leitungen Nr. JVe , die mit der Pumpe Nr. JPu verbunden sind | |
| (Gleichung 2.730) | |
| Ende der Do-Schleife. |
Ergänzen der NPu Gleichungen Nr. J4+1 bis J4+NPu zur Begrenzung des Pumpendrucks auf PPumax bzw. des Pumpenstroms auf QPuMax:
| Für JPu = 1 bis NPu tue folgendes: | |
| Wenn PuVar = 2, dann gilt | (Druckgeregelte Pumpe) |
| PPu = PPuMax | |
| sonst gilt | (Konstantpumpe) |
| QPuMax (JPu) = Summe(QVe( JVe )) aller Leitungen Nr. JVe , die mit der Pumpe Nr. JPu verbunden sind | |
| (Gleichung 2.730) | |
| endif | |
| Ende der Do-Schleife. |
Damit ist das Gleichungssystem eigentlich vollständig. Es wurden NGlei+NTa+NVe+2 NPu = NGlei1 linear unabhängige Gleichungen aufgestellt mit ebenso vielen unbekannten Variablen, für die genau eine Lösung zu erwarten ist. Mit einem Gauss-Algorithmus mit Pivotisierung (z.B. mit der Routine SIMQ) ist dieses Gleichungssystem lösbar.
Das Gleichungssystem soll aber mit dem GMRES-Verfahren mit ILU-Konditionierung gelöst werden. Dieses Verfahren fordert, dass die Hauptdiagonale der Matrix vollbesetzt ist, d.h. dass auf dieser Diagonale kein Koeffizient mit dem Wert Null auftritt. Diese Forderung ist aber bei diesem Gleichungssystem nicht immer erfüllt. Wenn für eine oder mehrere Pumpen Nr. JPu gilt: PuVar(JPu) = 1 (Konstantpumpe), dann wird im letzten Gleichungsblock die Gleichung (2.730) aufgestellt. In diesem Fall steht in der Hauptdiagonale der Gleichung Nr. J4+JPu eine Null, weil die unbekannte Variable PTa(JPu) in dieser Gleichung nicht vorkommt. Das betrifft im oben dargestellten Programmablauf den Block der letzten NPu Gleichungen und hier den 2.Fall. Dem kann abgeholfen werden, indem eine der bereits vorhandenen anderen Gleichungen, die in der Spalte (J4+JPu) einen von Null verschiedenen Koeffizienten aufweist, zu der Gleichung addiert wird. Geeignete Gleichungen findet man im Block der Gleichungen Nr. J2+1 bis J2+NVe. Das sind die Gleichungen der Gerätekennlinien. Deshalb ist nun noch für diesen speziellen Fall die Routine KoMa4 entsprechend zu ergänzen:
Für JVe = 1 bis NVe tue folgendes:
Wenn PuVar =1 und (PnPu≥PnTa oder das Gerät in der Leitung kein Rückschlagventil aufweist),
dann addiere die Gleichung Nr. J2+NVe:
QVe(JVe)=f(PPu(Ve(1,JVe))-PTa(Ve(2,JVe))) (Funktion der Gerätekennlinie)
zur Gleichung Nr. J4+NPu:
QPuMax (JPu) = Summe(QVe( JVe )) aller Leitungen Nr. JVe , die mit der Pumpe Nr. JPu verbunden sind
endif.
Damit ist der Programmablauf für die Berechnung der Koeffizientenmatrix des Gleichungssystems und der rechten Seiten komplett.
Mit diesem Entwurf des Programmablaufs kann der Quellcode für die Routine KoMa4 für eine ungepackte Koeffizientenmatrix geschrieben und getestet werden. Den kommentierten Quellcode der Routine "KoMa4" findest Du in der Textdatei gleichen Namens "KoMa4.f" Anschließend kann daraus der Quellcode für die Routine "KoMa4_pack" abgeleitet werden und ebenfalls getestet werden. Dieses stufenweise Vorgehen erleichtert es, Programmfehler zu finden.
Jeder, der dieses Programm evtl. um einen neuen Gerätetyp in den Verbindungsleitungen erweitern möchte, muss die Routine KoMa4_pack bearbeiten. Die Routine ist Bestandteil des Kerns der Berechnungen und Programmierfehler können hier die gesamte Berechnung verderben. Deshalb ist hier mit besonderer Umsicht vorzugehen und die Ergebnisse sind anschließend eingehend zu überprüfen.
zurück weiterDie Koeffizientenmatrix K bekommt der Anwender normaler Weise nicht zu Gesicht. Um den prinzipiellen Aufbau dieser Matrix einmal zu zeigen, soll aber hier diese Matrix an einem ganz kleinen Beispiel dargestellt werden:
Angenommen wird ein Gleitschuh, dessen Spaltfläche in nur 5·5 Flächenelemente aufgeteilt ist, gemäß Bild 3.40.
Anordnung der Schmiertaschen (Steuerfeld KX) JX,JZ=1 2 3 4 5 1 0 0 0 0 0 2 0 0 0 0 0 3 0 -1 0 -2 0 4 0 0 0 0 0 5 0 0 0 0 0Bild 3.40: Diskretisierte Spaltfläche eines Gleitschuhs, dargestellt anhand des Steuerfeldes KX
In dem Schmierspalt sind 2 Schmiertaschen angeordnet, die jeweils nur aus einem Flächenelement bestehen. Jede Schmiertasche ist mit je einer Verbindungsleitung mit je einer Schmiermittelpumpe verbunden. In den Verbindungsleitungen ist je eine Kapillare ohne Rückschlagventil angeordnet.
Daraus ergeben sich folgende Daten für das Gleichungssystem:
| NTa | =2 | Anzahl der Schmiertaschen |
| NVe | =2 | Anzahl der Verbindungsleitungen |
| NPu | =2 | Anzahl der Schmiermittelpumpen |
| NGlei | = NX·NZ-NTa = 5 · 5 -2= = 23 |
Anzahl der Feldelemente (Gitterpunkte), für die der Schmierfilmdruck berechnet werden muss |
| NGlei1 | = NGlei+NTa+NVe+2·NPu = = 31 |
Anzahl der unbekannten Variablen = Anzahl der Gleichungen |
Bild 3.41 zeigt die vollständige ungepackte Koeffizientenmatrix und die rechten Seiten des linearen Gleichungssystems für die Lösung dieses kleinen Beispiels für den ersten zu berechnenden Zeitpunkt.

Bild 3.41: Aufbau der ungepackten Koeffizienten Matrix K und der rechten Seite des linearen Gleichungssystems zur Berechnung des Schmierfilmdrucks und der primären Ergebnisdaten des peripheren Schmiersystems in der Hauptrechnung
Die ersten NGlei Gleichungen sind die Differenzengleichungen zur Approximation der Reynoldsschen Differentialgleichung zur Berechnung der Schmierfilmdruckverteilung. Sie machen den größten Teil des Gleichungssystems aus (siehe dazu Abschnitt 3.4.1). Die Erzeugung der Gleichungen und die Eintragung in die Koeffizientenmatrix und den Vektor der rechten Seiten erledigt die Routine KoMa2, wenn es Schmiertaschen gibt, oder KoMa1, wenn es keine Schmiertaschen gibt.
Die nächsten NTa Gleichungen bilden die Volumenbilanz in den Schmiertaschen ab. Für jede Schmiertasche wird genau eine Gleichung aufgestellt (siehe dazu Abschnitt 3.4.2). Die Erzeugung der Gleichungen und die Eintragung in die Koeffizientenmatrix und den Vektor der rechten Seiten erledigt die Routine KoMa3.
Die nächsten NVe Gleichungen repräsentieren die Gleichungen für die Kennlinien der Drosselgeräte in den Verbindungsleitungen. Sie stellen den Zusammenhang zwischen dem Pumpendruck PPu, dem Schmiertaschendruck PTa der angeschlossenen Schmiertasche und dem Schmiermittelstrom QVe in der entsprechenden Verbindungsleitung dar.
Die nächsten NPu Gleichungen stellen die Aufteilung des Pumpenstroms QPu auf die Ströme QVe der angeschlossenen Verbindungsleitungen dar.
Die letzten NPu Gleichungen legen den Pumpendruck PPu=PPuMax fest, wenn die jeweilige Pumpe aktuell als druckgeregelte Pumpe betrieben wird, bzw. sie legen den Pumpenölstrom QPu=QPuMax fest, wenn die Pumpe aktuell als Konstantpumpe arbeitet. Zu den letzten NPu Gleichungen werden bei Bedarf noch ausgewählte Gleichungen aus dem Block der Gleichungen Nr. NGlei+NTa+1 bis NGlei+NTa+NVe addiert (siehe dazu Abschnitt 3.4.3.2). Die letzten 3 Gleichungsblöcke enthalten meist recht triviale Gleichungen. Erzeugt werden sie durch die Routine KoMa4.
Die NGlei1 unbekannten Variablen sind passend zur Reihenfolge der Gleichungen sortiert. Zur besseren Anschaulichkeit wurden in Bild 3.41 die Blöcke der verschiedenen Gleichungen und die Blöcke der verschiedenen Unbekannten P, PTa, QVe, QPu und PPu durch eingetragene Linien getrennt. Außerdem wurden alle Koeffizienten, die von Null verschiedene Werte aufweisen, gelb hinterlegt. Die Koeffizienten der Hauptdiagonalen sind schwarz umrahmt. Es zeigt sich, dass schon bei diesem kleinen Beispiel die Matrix nur dünn belegt ist, d.h. dass die meisten Koeffizienten Null sind. Dieses Verhältnis wird bei üblicher Gitterteilung noch wesentlich extremer, weil sich die Anzahl der Koeffizienten pro Gleichung nur in den wenigen Gleichungen der 4 letzten Gleichungsblöcke erhöhen kann.
Die ungepackte Matrix ist noch einigermaßen übersichtlich. Sie wird in SIRIUS aber nur zu Testzwecken während der Programmentwicklung und zur Fehlersuche verwendet. Standardmäßig wird programmintern diese Matrix direkt in gepackter Form erzeugt. Hier werden die Aufgaben der Routinen KoMa1, KoMa2, KoMa3 und KoMa4 durch die Routinen KoMa1_pack, KomA2_pack, KoMa3_pack und KoMa4_pack ersetzt.
Für dieses einfache Beispiel soll jetzt auch die gepackte Matrix gezeigt werden.
Kontrolldruck der kompletten gepackten Koeffizientenmatrix
NGlei= 23 NTa= 2 NVe= 2 NPu= 2 NGlei1= 31
M Kv(M) Kc(M) JGlei Kp(JGlei) R(JGlei)
1 -140.5285 1 1 0 -18.7371
2 33.3333 2 2 3 -5.4038
3 13.5095 6 3 7 -5.4038
4 25.0000 1 4 11 -5.4038
5 -90.5285 2 5 15 -18.7371
6 25.0000 3 6 18 -13.3333
7 13.5095 7 7 22 0.0000
8 25.0000 2 8 27 0.0000
9 -90.5285 3 9 32 0.0000
10 25.0000 4 10 37 -13.3333
11 13.5095 8 11 41 -20.0000
12 25.0000 3 12 45 0.0000
13 -90.5285 4 13 50 -20.0000
14 25.0000 5 14 54 -13.3333
15 13.5095 9 15 58 0.0000
16 33.3333 4 16 63 0.0000
17 -140.5285 5 17 68 0.0000
18 13.5095 10 18 73 -13.3333
19 10.1321 1 19 77 -18.7371
20 -120.2642 6 20 80 -5.4038
21 33.3333 7 21 84 -5.4038
22 10.1321 11 22 88 -5.4038
23 13.5095 2 23 92 -18.7371
24 25.0000 6 24 95 0.0000
25 -90.5285 7 25 101 0.0000
26 25.0000 8 26 107 0.2262
27 27.0190 24 27 110 0.2262
28 10.1321 3 28 113 5.0930
29 25.0000 7 29 114 2.0372
30 -70.2642 8 30 115 -4.8667
31 25.0000 9 31 117 -1.8110
24 25.0000 6
25 -90.5285 7
26 25.0000 8
27 27.0190 24
28 10.1321 3
29 25.0000 7
...
...
93 13.5095 18
94 33.3333 22
95 -140.5285 23
96 -0.4244 7
97 -1.0472 11
98 -1.0472 12
99 -0.4244 15
100 2.9432 24
101 -1.0000 26
102 -0.4244 9
103 -1.0472 12
104 -1.0472 13
105 -0.4244 17
106 2.9432 25
107 -1.0000 27
108 7.7280 24
109 1.0000 26
110 -7.7280 30
111 7.7280 25
112 1.0000 27
113 -7.7280 31
114 1.0000 28
115 1.0000 29
116 7.7280 24
117 -7.7280 30
118 7.7280 25
119 -7.7280 31
Die gepackte Matrix besteht aus den 3 Vektoren Kv(M), Kc(M) und Kp(NGlei1). M ist hier die Anzahl der Koeffizienten, die nicht gleich Null sind. In dem Vektor Kv sind alle Nicht-Null-Koeffizienten zeilenweise und lückenlos hintereinander abgelegt. Der Vektor Kc gibt zu jedem Nicht-Null-Koeffizienten an, in welcher Spalte er in der ungepackten Matrix stehen würde. Die Vektoren Kv und Kc enthalten jeweils M Elemente, wobei die Elemente des Vektors Kc ganzzahlig sind. Der Pionter-Vektor Kp(NGlei+1) enthält NGlei+1 ganze Zahlen. Die erste Zahl ist die Null. In fortlaufender Folge enthält er dann die Nummern des letzten Nicht-Null Koeffizienten jeder Zeile. Auf diese Weise werden zum Abspeichern jedes Koeffizienten und seiner Lage in der Matrix 3 Zahlen benötigt. Diese 3 Vektoren benötigen aber wesentlich weniger Speicherplatz als die komplette ungepackte Matrix K. Diese Angaben sind ausreichend, damit das GMRES-Verfahren und das Konditionierungsverfahren immer auf die richtigen Koeffizienten zugreifen können.
Die hier gezeigten Darstellungen der Matrizen kann sich auch der versierte Anwender vom Programm SIRIUS anzeigen lassen. Dazu sind im Quelltext der Routinen FilmDruck1 und FilmDruck2 unter der Kommentarzeile "Kontrolldruck der Koeffizientenmatrix" bereits 4 deaktivierte Befehlsblöcke abgelegt, mit denen jeweils die komplette gepackte Matrix (gemäß hier gezeigter Tabelle), die letzten Koeffizienten der gepackten Matrix, die komplette ungepackte Matrix (gemäß Bild 3.41) oder der rechte untere Quadrant der ungepackten Matrix angezeigt werden kann. Dazu ist die Datei "FilmDruck1.f" bzw. "Filmdruck2.f" mit dem Quelltext dieser Routinen zu öffnen und die Deaktivierung der Befehlszeilen aufzuheben, indem der Buchstabe "c" am Anfang der jeweiligen Befehlszeilen gelöscht wird. Anschließend ist die Datei wieder abzuspeichern und der Quelltext erneut zu kompilieren. Nach dem Neustart des Programms wird jetzt vor jeder Lösung des Gleichungssystems die Matrix bzw. ein Teil davon angezeigt. Das kann ein Hilfsmittel im Rahmen der Weiterentwicklung des
Die vollständigen Daten zu dem hier gezeigten Demonstrationsbeispiel findest Du in der Datei "Demo23.txt".
zurück weiterUrsprünglich wurde zur Lösung des Gleichungssystems ein Gaußsches Eliminationsverfahren verwendet (siehe Abschnitt 3.4.5.3). Da es trotz schneller werdender Rechner bei den aktuell üblichen Gitterteilungen noch recht langsam arbeitet, wurde ein für diese Aufgabe geeignetes schnelleres Verfahren gesucht. Wie bei der Simulation vieler technischer Sachverhalte ist die Koeffizientenmatrix des Gleichungssystems auch hier nur dünn besetzt. Dafür wurden parallel zur Entwicklung leistungsfähiger Computer und komplexer werdender Aufgaben eine Reihe leistungsfähiger Verfahren entwickelt, aus denen ein geeignetes ausgewählt wurde. Der Autor hat sich für das GMRES-Verfahren (Abschnitt 3.4.5.1) in Kombination mit einer Vorkonditionierung der Matrix mittels einer ILU-Zerlegung entschlossen (Abschnitt 3.4.5.2).
zurück weiterWikipedia gibt folgende Kurzbeschreibung des Verfahren: "Das GMRES-Verfahren (für Generalized minimal residual method) ist ein iteratives numerisches Verfahren zur Lösung großer, dünnbesetzter linearer Gleichungssysteme. Das Verfahren ist aus der Klasse der Krylow-Unterraum-Verfahren und insbesondere auch für nicht-symmetrische Matrizen geeignet. In exakter Arithmetik, also wenn ohne Rundungsfehler gerechnet wird, liefert das Verfahren nach endlich vielen Schritten die exakte Lösung. Interessanter ist es jedoch als näherungsweises Verfahren, da es mit einer geeigneten Vorkonditionierung auch Gleichungssysteme mit Millionen Unbekannten in wenigen Iterationen mit befriedigender Genauigkeit lösen kann. Damit stellt es eine Art Black Box-Löser für dünnbesetzte lineare Gleichungssysteme dar. Es wurde 1986 von Yousef Saad und Martin H. Schultz entwickelt. ..." [32] Hier wird auch bereits ein guter Überblick über den theoretischen Hintergrund und die Funktionsweise des Verfahrens gegeben.
Eine weitere informative Quelle zu diesem Verfahren ist das Lehrbuch von Meister [11]. Es liefert für dieses und andere Verfahren auch Quellcode in der Programmiersprache MATLAB als Vorlage.
Eine freie Quelle einer lauffähigen Routine des Verfahrens in der Programmiersprache FORTRAN wurde nicht gefunden, deshalb wurde vom Autor anhand der hier angegebenen Quellen das Verfahren in der Sprache FORTRAN77 neu programmiert. Es liegt vor in der Routine "GMRES_ILU_pack", die als kommentierter Quellcode in der gleichnamigen Textdatei "GMRES_ILU_pack.f" abgelegt ist. Es wurde eine Variante des Verfahrens mit Restart programmiert. Die Anzahl der Iterationen bis zu einem Restart ist programmintern mit dem Parameter MaxIt=30 fest vorgegeben, da von diesem Wert die erforderliche Größe einiger Hilfsdatenfelder abhängt. Die Anzahl der Restarts, die das Programm ausführt, bevor es wegen Nicht-Konvergenz abbricht, ist durch den Parameter Maxstart angegeben. Standardmäßig ist der Wert mit 10 vorgegeben, so dass das Programm nach maximal 30·10=300 Iterationen wegen Nicht-Konvergenz abbricht. In SIRIUS kann über das Untermenü "Programminterne Parameter ändern" im Hauptmenü "Ende der Eingabe" der Parameter Maxstart vom Anwender ohne Eingriff in den Quellcode zeitweilig geändert werden.
Neben der Bedingung einer dünnbesetzten regulären Matrix, deren Hauptdiagonale voll besetzt sein muss, stellt das GMRES-Verfahren keine weiteren speziellen Anforderungen an das zu lösende Gleichungssystem. Die Routine "GMRES_ILU_pack" ist auch nicht speziell auf die Belange der Lagerberechnung zugeschnitten. Deshalb könnte die Routine "GMRES_ILU_pack" auch zur Lösung anderer Probleme in andere Programme implementiert werden. Es müssten lediglich die erforderlichen Feldgrößen, die in FORTRAN77 fest vorzugeben sind, im Quelltext entsprechend angepasst werden. Das erfolgt durch Festlegen eines geeigneten Wertes für den Parameter NGMax.
Gegenüber dem Gaußschen Eliminationsverfahren brachte das GEMRES-Verfahren in Kombination mit der ILU-Zerlegung bei einer üblichen Gitterteilung der Schmierspaltfläche von ca. 300·20=6000 Gitterpunkten und damit ca. 36 Mio. Koeffizienten eine Verkürzung der Rechenzeit um den Faktor 1000. Bei direkter Erzeugung der gepackten Matrix wird auch Speicherplatz eingespart, weil keine ungepackte Matrix mehr erzeugt werden muss, deren Koeffizienten fast alle Null sind. Ein weiterer Vorteil ist, dass bei einer Vergrößerung der Anzahl der Gleichungen die Rechenzeit nur proportional ansteigt mit der Anzahl der Gleichungen, im Gegensatz zum Gauß-Verfahren, wo die Rechenzeit mit dem Faktor n³ ansteigt.
zurück weiterWikipedia gibt folgende kurze Erklärung für den Begriff:" In der numerischen Mathematik bezeichnet Vorkonditionierung eine Technik, mittels derer ein Problem so umgeformt wird, dass die Lösung erhalten bleibt, sich jedoch für das gewählte numerische Lösungsverfahren positive Eigenschaften wie bessere Kondition oder schnellere Konvergenz ergeben.
Die gebräuchlichste Form der Vorkonditionierung ist die lineare, bei der ein lineares Gleichungssystem äquivalent umgeformt wird. Diese Art der Vorkonditionierung findet insbesondere bei der Lösung des Gleichungssystems mittels Krylow-Unterraum-Verfahren Anwendung. ... " [38]
Die ILU-Zerlegung wird durch Wikipedia in folgender Weise kurz beschrieben:" Als ILU-Zerlegung (von incomplete LU-Decomposition) oder unvollständige LU-Zerlegung bezeichnet man in der numerischen Mathematik die fehlerbehaftete Zerlegung einer Matrix 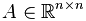 in das Produkt einer unteren Dreiecksmatrix L und einer oberen Dreiecksmatrix U
in das Produkt einer unteren Dreiecksmatrix L und einer oberen Dreiecksmatrix U
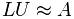
bei der von den Zerlegungsmatrizen L und U nur die Einträge einer vorgegebenen Besetzungsstruktur berechnet werden. ...
Die ILU-Zerlegung wird erfolgreich als Vorkonditionierer zur Beschleunigung der iterativen Lösung großer dünnbesetzter linearer Gleichungssysteme mittels Krylow-Unterraum-Verfahren eingesetzt. Es werden dabei keine Eigenschaften des eigentlichen Problems (meist die numerische Lösung einer partiellen Differentialgleichung) ausgenutzt. Damit ist sie nicht auf bestimmte Problemklassen beschränkt und hat Einzug in viele Bereiche der numerischen Simulation gefunden, beispielsweise in der numerischen Strömungsmechanik ist die Technik weit verbreitet. Zuerst erwähnt wurde das Verfahren 1960 von Richard S. Varga und Nikolai Iwanowitsch Bulejew (N. I. Buleev). Eine genauere Analyse wurde 1977 von J. A. Meijerink und van der Vorst veröffentlicht. ..." [35]
Die Skripte zur Numerischen Mathematik von Lube [10] geben eine hilfreiche Darstellung für eine Umsetzung in ein Programm.
Das GMRES-Verfahren wird erst schnell durch eine geeignete Vorkonditionierung. In der Literatur wird dafür das Verfahren der ILU-Zerlegung empfohlen, weshalb sich der Autor auch für diese Vorkonditionierung entschieden hat. Eine freie Quelle einer lauffähigen Routine des Verfahrens der ILU-Zerlegung wurde nicht gefunden, deshalb wurde vom Autor anhand der hier angegebenen Quellen das Verfahren in der Sprache FORTRAN77 neu programmiert. Es liegt vor in der Routine "ILU_Zerlegung_pack", die als kommentierter Quellcode in der gleichnamigen Textdatei "ILU_Zerlegung_pack.f" abgelegt ist.
zurück weiterWikipedia gibt folgende Kurzbeschreibung des Verfahren: "Das Gaußsche Eliminationsverfahren oder einfach Gauß-Verfahren (nach Carl Friedrich Gauß) ist ein Algorithmus aus den mathematischen Teilgebieten der linearen Algebra und der Numerik. Es ist ein wichtiges Verfahren zum Lösen von linearen Gleichungssystemen und beruht darauf, dass elementare Umformungen zwar das Gleichungssystem ändern, aber die Lösung erhalten. Dies erlaubt es, jedes eindeutig lösbare Gleichungssystem auf Stufenform zu bringen, an der die Lösung durch sukzessive Elimination der Unbekannten leicht ermittelt oder die Lösungsmenge abgelesen werden kann.
Die Anzahl der benötigten Operationen ist bei einer n x n-Matrix von der Größenordnung n³. In seiner Grundform ist der Algorithmus anfällig für Rundungsfehler, aber mit kleinen Modifikationen (Pivotisierung) stellt er für allgemeine lineare Gleichungssysteme das Standardlösungsverfahren dar und ist Teil aller wesentlichen Programmbibliotheken für numerische lineare Algebra ..." [31]
Standardmäßig wird dieses Verfahren in SIRIUS nicht mehr verwendet, da es zu langsam arbeitet. Wegen der Schwierigkeiten, fehlerfreie Routinen zur Erstellung der gepackten Koeffizientenmatrix zu schreiben, wurde das Verfahren aber nicht vollständig aus dem Programm entfernt. Es kann zu Testzwecken wieder aktiviert werden. Siehe dazu Abschnitt 3.4.5.4.
Der Quellcode des Verfahrens liegt als Routine SIMQ in der gleichnamigen Textdatei "SIMQ.f" vor. Es stammt aus einer Programmbibliothek des Rechenzentrums der VVB Schiffbau Rostock, aus der es im Zeitraum zwischen 1974 und 1978 entnommen wurde. Der Autor der Routine ist nicht bekannt. Es stellt ein Gauß-Verfahren mit Pivotisierung dar.
zurück weiterStandardmäßig arbeitet das Programm SIRIUS zur Lösung des linearen Gleichungssystems innerhalb der Hauptrechnung mit einer gepackten Matrix, die durch die Routinen "KoMa1_pack" bzw. "Koma2_pack", "KoMa3_pack" und "KoMa4_pack" direkt erzeugt wird und durch das schnelle GMRES-Verfahren mit Vorkonditionierung (Routine "GMRES_ILU_pack") gelöst wird. Diese Routinen werden durch die übergeordneten Routinen "FilmDruck1" und "FilmDruck2" aufgerufen.
Um bei einer Überarbeitung oder Erweiterung des Programms die schwierige Programmierung der direkten Erzeugung gepackter Matrizen überprüfen zu können, kann die Berechnung über den langsameren Weg der Arbeit mit ungepackten Matrizen einfach aktiviert werden. Dazu ist bereits je eine Variante der Routinen "FilmDruck1" und "FilmDruck2", die mit ungepackter Matrix arbeiten, vorbereitet und in den deaktivierten Quellcode-Dateien "FilmDruck1_unpack.f_" und "FilmDruck2_unpack.f_" abgelegt. In diesen Routinen wird zunächst mit den Unterroutinen "KoMa1", "KoMa2", "KoMa3" und "KoMa4" die ungepackte Matrix K erzeugt. Anschließend wird diese mit der Unterroutine "MatrixPacken" in eine gepackte Matrix umgewandelt und das Gleichungssystem mit der Routine "GMRES_ILU_pack" gelöst.
Um diese Berechnungsvariante zu aktivieren, sind die dazu erforderlichen Quellcode-Dateien zu aktivieren, indem die Dateiendungen ".f_" auf ".f" geändert werden. Das sind die Dateien
"FilmDruck1_unpack.f_",
"FilmDruck2_unpack.f_",
"KoMa1.f_",
"KoMa2.f_",
"KoMa3.f_",
"KoMa4.f_" und
"MatrixPacken.f_".
Außerdem müssen die beiden Quellcode-Dateien
"FilmDruck1.f" und
"FilmDruck2.f"
deaktiviert werden, indem die Dateierweiterungen ".f" in ".f_" geändert werden. Die dann auch nicht benötigten Quellcode-Dateien "KoMa1_pack.f" bzw. "Koma2_pack.f", "KoMa3_pack.f" und "KoMa4_pack.f" können ebenfalls deaktiviert werden, müssen aber nicht. Anschließend muss der gesamte Quellcode neu kompiliert (siehe Abschnitt 4.2.8) und danach die neu Programmdatei "SIRIUS.exe" gestartet werden.
Es kann auch ganz auf die Arbeit mit einer nachträglich gepackten Matrix und der Lösung des Gleichungssystems mit dem GMRES-Verfahren verzichtet werden. Stattdessen wird dann die ungepackte Matrix direkt mit dem Gaußschen Eliminationsverfahren (Routine SIMQ) gelöst. Dazu sind zusätzlich in den inzwischen aktivierten Quellcode-Dateien "FilmDruck1_unpack.f", "FilmDruck2_unpack.f" folgende Befehlszeilen zu ändern:
...
call MatrixPacken(K,NGlei1,Kv,Kc,Kp,M)
call GMRES_ILU_pack(M,Kv,Kc,Kp,R,NGlei1,R1,Tol,MaxStart,Konvergenz)
...
c call SIMQ(K,R,NGlei1,Konvergenz)
c if(Konvergenz==1)then
c write(*,*)
c write(*,*)'FEHLERMELDUNG 401 in FilmDruck1_unpack:'
c write(*,*)' Die Gleichungen sind nicht linear unabhaenig.'
c write(*,*)' Die Berechnung wird abgebrochen.'
c write(*,*)'Weiter mit ENTER:'
c read(*,*)
c Status=9
c return
c endif
c do 99 jj=1,NGlei1
c99 R1(jj)=R(jj)
...
Bei allen gezeigten Befehlszeilen, die mit einem "c" in der ersten Spalte beginnen, ist dieses "c" zu entfernen. Bei allen gezeigten Befehlszeilen, wo dieses "c" fehlt, ist ein "c" einzufügen.
Die erweiterte Reynoldssche Differentialgleichung (Theo=2) ist nicht linear und kann deshalb mit dem Differenzenverfahren nur iterativ gelöst werden. Bei der Berechnung der Druckverteilung können deshalb Instabilitäten entstehen, die sich aufschaukeln und schließlich zum Abbruch der Berechnung führen (siehe ausführliche Erläuterung dazu im Abschnitt 4.9.2.1). Prinzipiell lassen sich diese Probleme durch feinere Gitterteilungen ΔX und/oder kleinere Zeitschrittweiten ΔT beseitigen. Das kann aber zu erheblich höherem Berechnungsaufwand führen und evtl. auch die Kapazität des Berechnungsprogramms oder die Geduld des Anwenders überfordern.
Mit Hilfe empirischer Untersuchungen und einiger Überlegungen wurden Wege gefunden, diese Instabilitäten, wenn auch nicht vollständig zu beseitigen, so doch erheblich zu dämpfen, so dass mit relativ groben Gitterteilungen NX und Zeitschrittweiten NT bereits gute Ergebnisse erzielt werden und so Berechnungszeit gespart wird. Das wird durch die Korrekturroutinen "Pglatt", "Fuell1", "KleiDru4" und "Pkorr6" realisiert. Da sie sich bewährt haben, sind sie fest in das Programm eingefügt.
Bild 3.45 zeigt die Flüssigkeitsverteilung im Schmierspalt zum Zeitpunkt JT=10 für ein schwellend belastetes Lager. Noch anschaulicher ist die dazugehörige Animation von 2 Lastzyklen. Die Daten zu diesem Demonstrationsbeispiel sind in der Datei "Demo24-1.txt" abgelegt. Die Animation und das Bild zeigen, dass die Berechnung stabil abläuft.
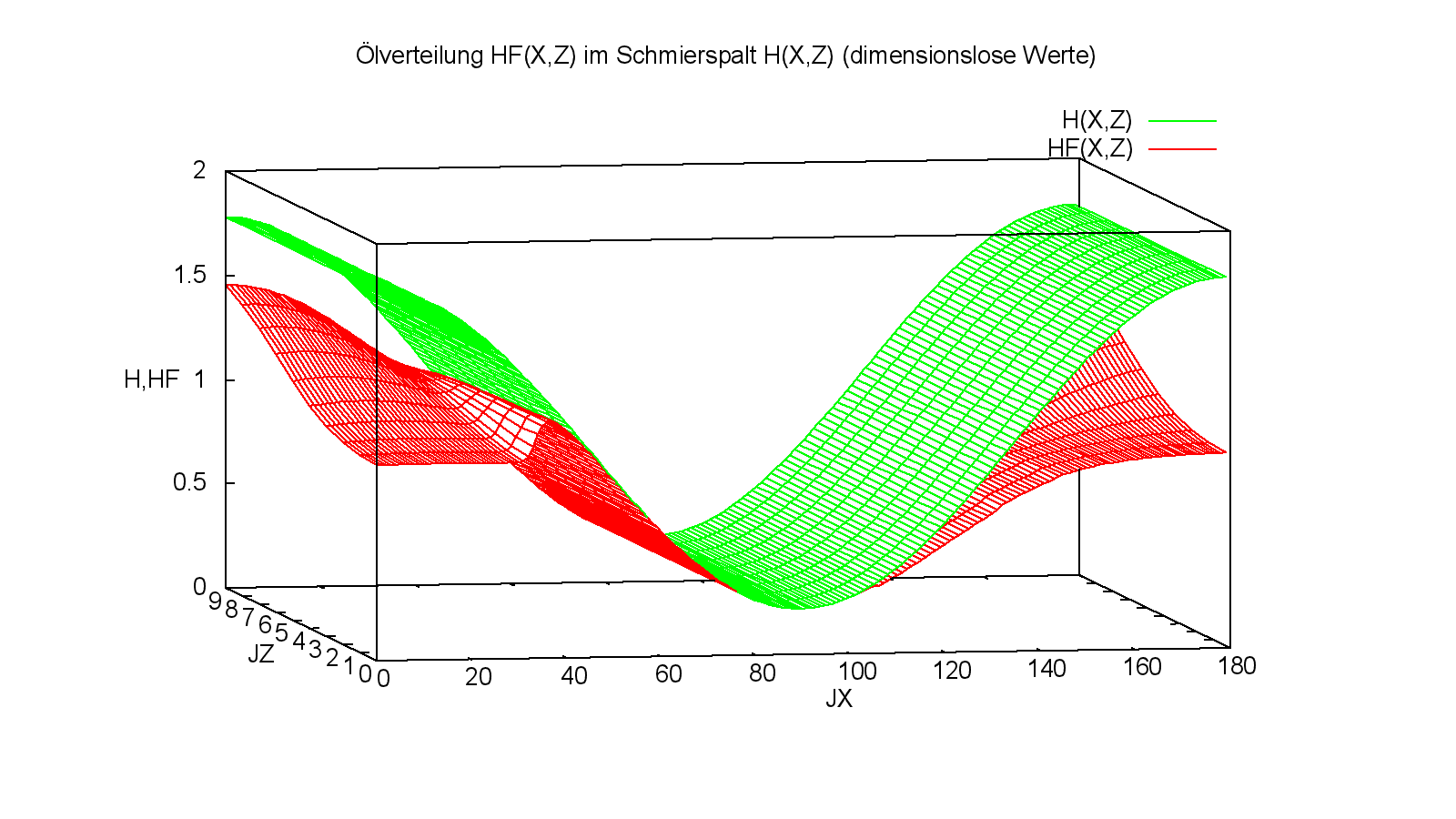
Bild 3.46 zeigt nun die Flüssigkeitsverteilung für das gleiche Beispiel für den gleichen Zeitpunkt der Berechnung. Hier wurden aber zuvor die Routinen "Pglatt" und "Pkorr6" im Programm deaktiviert. Der gezeigte Zeitpunkt ist der Zeitpunkt, zu dem erstmals eine Instabilität auftritt. Bild 3.47 zeigt dann den letzten Zeitpunkt der Berechnung bevor das Programm mit einer Fehlermeldung abbricht. Es zeigt, dass sich die Instabilität fast über den gesamten Schmierspalt ausgebreitet hat.
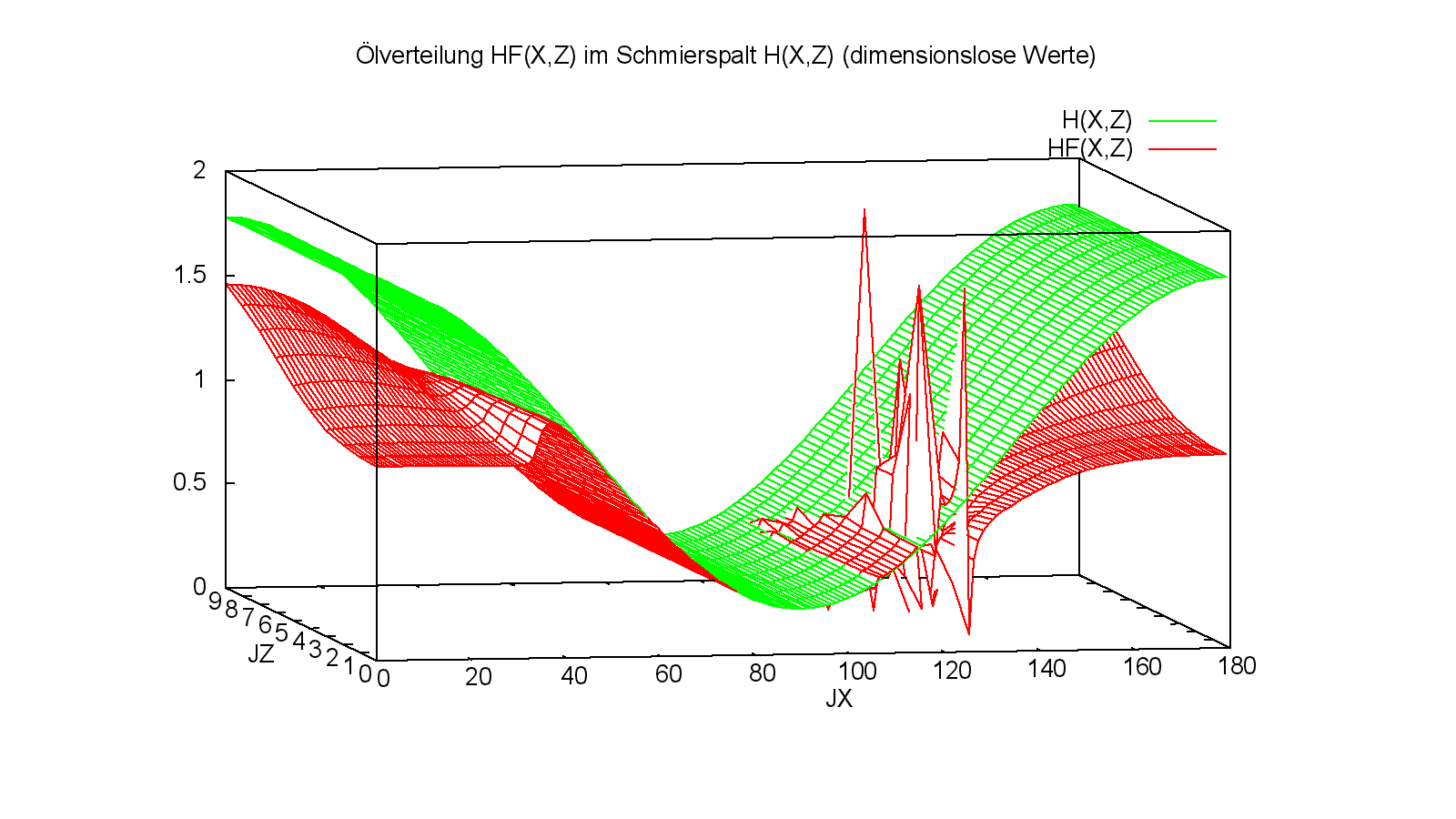
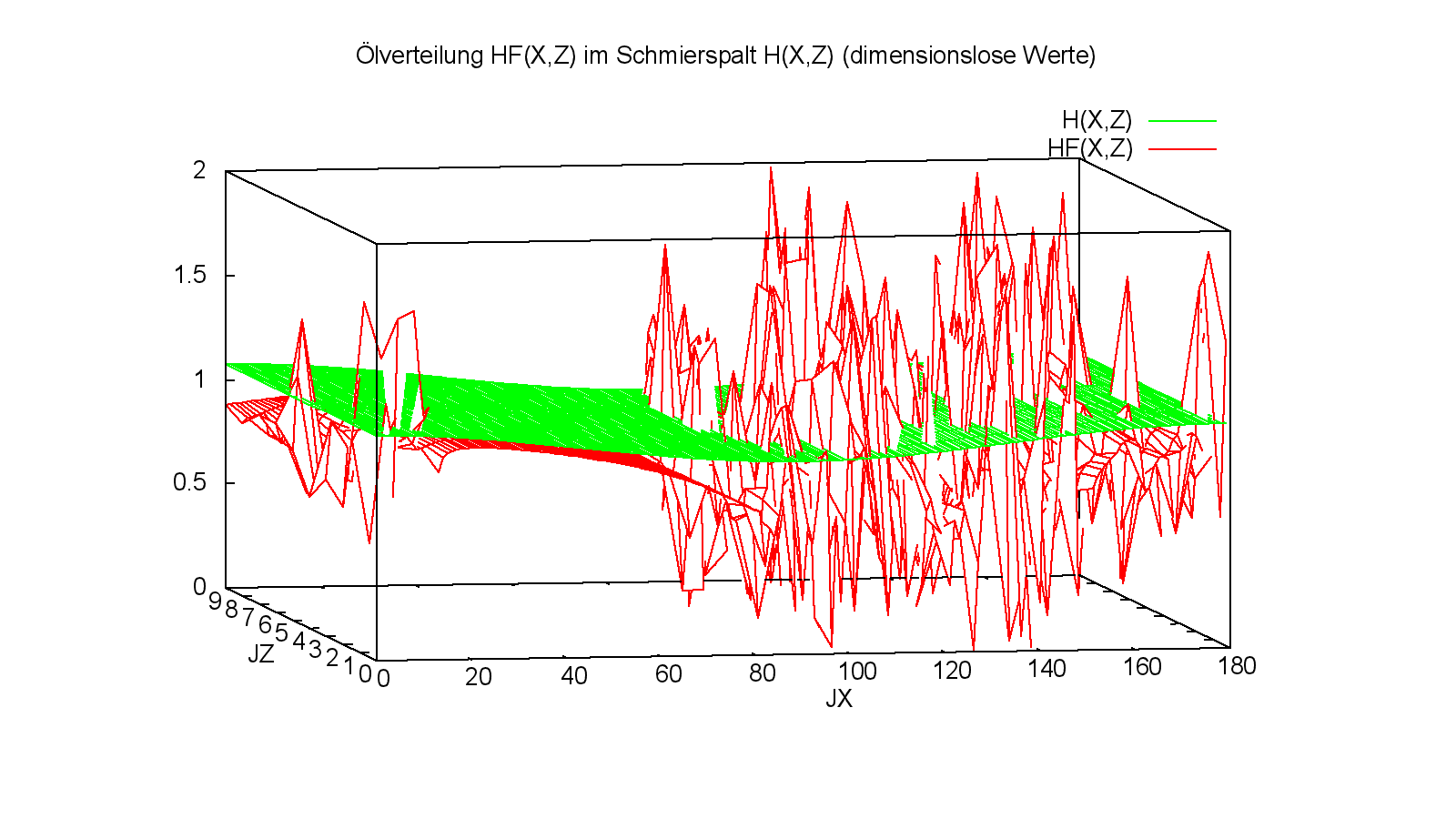
Die Ergebnisse dieser Berechnung sind in der Datei "Demo24-2.txt" abgelegt. Du kannst sie aber nur nachrechnen, wenn Du vorher im Quellcode der Routine "FilmDruck2" die Routinen "Pglatt" und "PKorr6" deaktivierst. Sonst würden wieder die Ergebnisse aus "Demo24-1.txt" erscheinen.
Wie gesagt, könnte man prinzipiell auch ohne die Korrekturroutinen auskommen. Dazu muss man nur die Gitterweite ΔX und die Zeitschrittweite ΔT ausreichend verkleinern. Im gezeigten Demonstrationsbeispiel musste dazu die Gitterweite ΔX halbiert und die Zeitschrittweite ΔT durch 3 geteilt werden. Das entspricht etwa einer 6-fachen Rechenzeit.
Das Bild 3.48 zeigt das wieder stabile Berechnungsergebnis ohne Korrekturroutinen aber mit aufwendigerer Berechnung. Die Ergebnisse sind fast identisch mit den Ergebnissen des Bildes 3.45.

Im folgenden Beispiel (Bild 3.49) wurden wieder die Eingabedaten des Demonstrationsbeispiels Demo24-1 verwendet. Es wurde dieses Mal im Quelltext nur die Routine "Pglatt" deaktiviert. Hier entsteht eine Instabilität im Bereich des Schmiermittelrückstaus vor dem Druckberganfang, der zu diesem welligen Verlauf der Schmiermittelverteilung führt. Im hier gezeigten Beispiel (Demo24-4.txt) tritt um den Zeitpunkt JT=32 nur eine kurze lokale Instabilität am Druckberganfang auf, die dann wieder abklingt. Unter ungünstigeren Bedingungen kann sie sich aber auch leicht aufschaukeln.
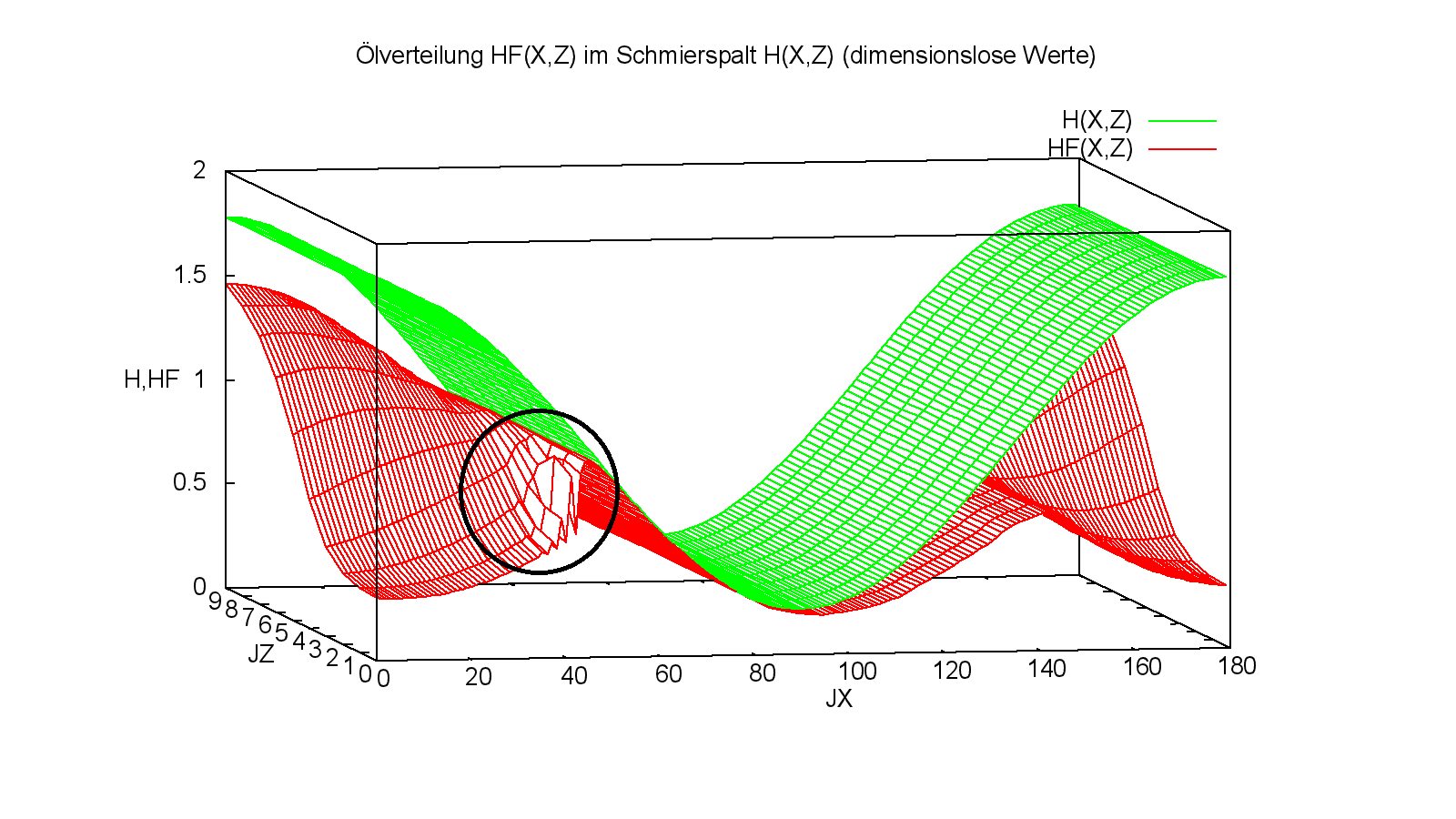
Es wurden empirische Untersuchungen mit verschiedenen Glättungsfunktionen durchgeführt, um den Aufbau dieser Schwingungen zu unterdrücken oder mindestens zu dämpfen. Die besten Ergebnisse wurden mit nachfolgender Glättungsfunktion erreicht
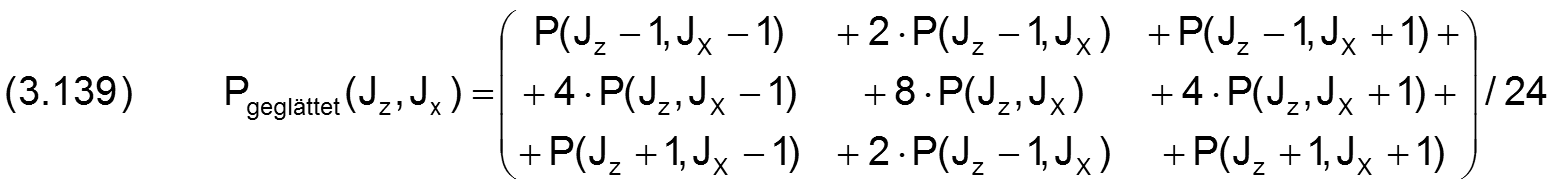
Mit der Routine "Pglatt" wurde diese Glättungsfunktion in das Programm eingebaut. Die Glättungsroutine wird nach jeder Berechnung des Druckverlaufs mit der erweiterten Reynoldsschen Differentialgleichung (Theo=2) von der übergeordneten Routine "FilmDruck2" aufgerufen. Die Glättung wird aber nur im Bereich niedriger Drücke ausgeführt. Als Obergrenze der Korrektur wird das Druckniveau des kleinsten Drucks am Lagerrand PRand1 bzw. PRand2 angenommen.
Mit dieser Druckkorrektur können einige Instabilitäten im Anfangsstadium gut gedämpft werden, so dass diese sich oft nicht aufschaukeln. Diese Instabilitäten lassen sich aber nicht immer verhindern. Siehe dazu auch die Abschnitte 4.9.2.1 und 4.9.2.2.
Plötzliche Druckschwankungen, z.B. infolge einer starken Lastrichtungsänderung, können für die iterative Berechnung des Druckverlaufs im Schmierspalt nach der erweiterten Reynoldsschen Gleichung (Theo=2) ebenfalls zum Problem werden. Wenn ein Druckberg oder ein Teil davon plötzlich zusammenbricht und zum Kavitationsgebiet wird, kommt es vor, dass das iterative Lösungsverfahren negative Drücke berechnet, obwohl diese hier nicht zulässig sind. Dieser Effekt ist z.B. in Bild 3.50 zu beobachten. Hier wurde das Demonstrationsbeispiel "Demo24-2" ohne die Korrekturprogramme "Pglatt" und "Pkorr6" berechnet.

Bild 3.50: Erstes instabiles Berechnungsergebnis des Programms SIRIUS ohne Korrekturroutinen "Pglatt" und "Pkorr6" (Bilddatei: Demo24-2-3d-Abw-P-H-HF-JT=10.png) (Animation: Demo24-2-3d-Abw-P-H-HF.wmv)
Um diesem Problem zu begegnen, wurde neben dem Glätten des Druckverlaufs ein weiteres Korrekturverfahren entwickelt, dass sich bewährt hat. Diesem Verfahren liegt folgende theoretische Überlegung zugrunde: Im Kavitationsgebiet, wo nur noch geringe Drücke und damit nur geringe Druckschwankungen herrschen, wird der Schmiermitteltransport fast ausschließlich durch Scherung angetrieben. D.h., dass die mittlere Schmiermittelgeschwindigkeit der halben Drehgeschwindigkeit der Welle entspricht. Wenn also die Schmierflüssigkeitsverteilung HF(Z,X,JT-1) aus dem vorhergehenden Zeitpunkt JT-1 bekannt ist, kann man die Schmiermittelverteilung HF(Z,X,JT) für den aktuellen Zeitpunkt JT gut abschätzen, indem man die bekannte vorhergehende Schmiermittelverteilung um den Weg Ω·ΔT/2 in Drehrichtung der Welle verschiebt. Da es zu der erweiterten Reynoldsschen Gleichung einen direkten Zusammenhang zwischen dem Schmierfilmdruck und dem örtlichen Füllungsgrad und damit auch zu der örtlichen Flüssigkeitsmenge HF=H·F im Schmierspalt gibt, kann man aus der verschobenen Schmiermittelverteilung den Schmiermitteldruck Pk(Z,X) im Kavitationsgebiet abschätzen mit
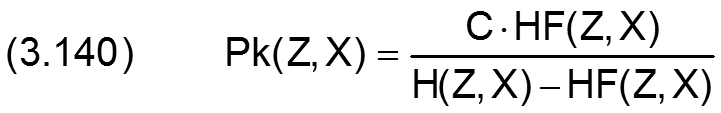
Da die Drücke rund um das Kavitationsgebiet höher sind, strömt zusätzlich zur reinen Scherströmung Schmiermittel in das Kavitationsgebiet. D.h., dass der exakt berechnete Schmiermitteldruck P(Z,X) größer, aber nicht kleiner sein kann, als der mit Pk(Z,X) abgeschätzte Schmierfilmdruck. D.h. außerdem, dass Pk(Z,X) als Untergrenze des möglichen Schmierfilmdruckes P(Z,X) angesehen werden kann und jeder berechnete Druck P(Z,X), der kleiner ist als Pk(X,Z), ist fehlerhaft. Damit ergibt sich eine plausible Korrekturmöglichkeit für die iterativ berechneten Drücke im Kavitationsgebiet: Alle Drücke P(Z,X)<Pk(Z,X) werden auf PK(Z,X) hochgesetzt. Damit entsprechen diese Werte vielleicht nicht ganz der exakten Lösung. Es hat sich aber gezeigt, dass sie eine noch recht gute Näherung darstellen. Vor allem wird damit verhindert, dass Werte kleiner oder gleich Null in die Berechnung des nächsten Zeitschrittes eingehen, was zu unsinnigen Ergebnissen oder zum Abbruch des Programms führen würde.
Die hier beschriebene Korrektur wird in 3 Teilschritten durch die 3 Routinen "Fuell1", KleiDru4" und "Pkorr6" ausgeführt. Die Routine "Fuell1" berechnet bereits zum vorhergehenden Zeitpunkt JT-1 aus der Druckverteilung die Schmierflüssigkeitsverteilung HF und verschiebt diese um den Betrag Ω·ΔT/2 in Wellendrehrichtung. Die Routine "KleiDru4" berechnet aus dem Feld der abgeschätzten örtlichen Verteilung HF der Schmierflüssigkeit den KorrekturDruck Pk. Die Routine "Pkorr6" vergleicht die aktuell berechnete Druckverteilung P(Z,X) mit den abgeschätzten kleinsten Drücken Pk(Z,X) und korrigiert gegebenenfalls damit P(Z,X).
Die Korrektur mit Pk erfolgt erst nach dem Glätten der Druckverteilung durch die Routine "Pglatt". Siehe vorhergehenden Abschnitt 3.4.6.1.
Diese Korrekturroutinen haben sich bewährt und sind im Programm fest eingebaut. Sie arbeiten unsichtbar und ohne Zutun des Programmanwenders und können nur durch Eingriff in den Quelltext außer Kraft gesetzt werden. Wenn Du das Programm ohne diese Korrektur testen willst, brauchst Du nur im Quellcode der Routine "FilmDruck2" den Aufruf der Routine "Pkorr6" deaktivieren. Nach dem Kompilieren des Quelltextes arbeitet das Programm ohne diese Korrektur.
Diese Korrekturen werden nur bei der Verwendung der erweiterten Reynoldsschen Differentialgleichung (Theo=2) angewendet. Die klassische Reynoldssche Differentialgleichung (Theo=1) benötigt diese Korrektur nicht. Hier werden berechnete negative Drücke entsprechend der "Gümbelschen Randbedingung" mit der Routine "Pkorr1" hochgesetzt.
zurück weiterMit Hilfe der Reynoldsschen Differentialgleichung kann man aus einer vorgegebenen Spaltgeometrie den Druckverlauf im Schmierspalt berechnen und durch Integration der Schmierspaltdrücke den resultierenden Vektor der Lagerbelastung [F1,F2].
In der Praxis ist die Problemstellung aber umgekehrt. Es ist eine stationäre Lagerbelastung oder ein zeitlicher Verlauf der Lagerbelastung gegeben. Infolge des Vektors der Lagerbelastung [F1(T),F2(T)] verlagert sich die Welle innerhalb des Lagerspielraums, bis der dadurch entstehende Schmierfilmdruck mit der Lagerbelastung im Gleichgewicht steht. Es ist also der Vektor der Wellenverlagerung [E1(T),E2(T)] zu ermitteln.
Deshalb musste eine algorithmierbare Suchstrategie entwickelt werden und als ein weiterer Iterationsprozess in das Berechnungsprogramm implementiert werden. Brökel [2] entwickelte eine entsprechende Suchstrategie und implementierte sie erstmals in das Programm SIRIUS.
Die nachfolgenden Abschnitte 3.4.7.1 bis 3.4.7.6 beschreiben die weiterentwickelte Lösung dieser Aufgabe ausführlich.
zurück weiterFormal kann man den Zusammenhang zwischen den Komponenten der Lagerbelastung F1 und F2 und der Spaltgeometrie E1 und E2 als die Funktionen funktion1 und funktion2 formulieren.
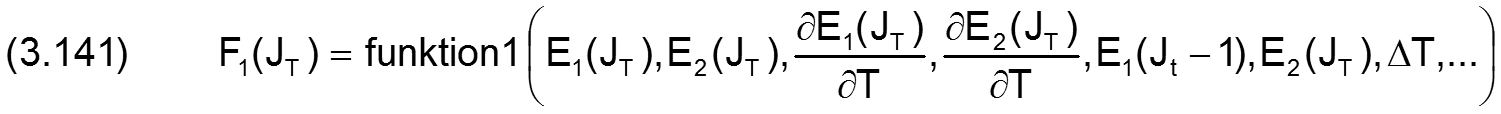
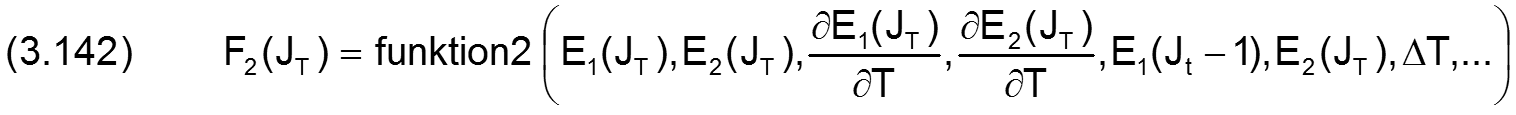
Es sind hier zunächst die 4 Variablen
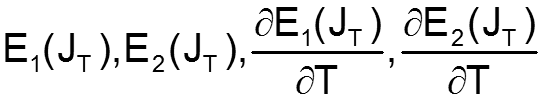
unbekannt. Die beiden Ableitungen kann man aber auch näherungsweise durch die beiden unbekannten E1(JT), E2(JT) und die beiden bereits bekannten Werte E1(JT-1),E2(JT-1) ausdrücken.
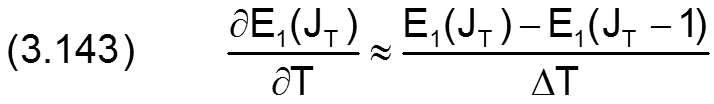
und
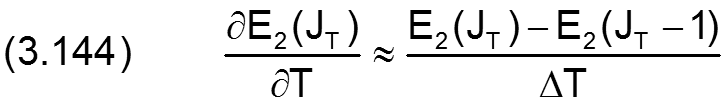
So lassen sich die beiden Funktionen um schreiben auf ein System mit nur noch 2 unbekannten Variablen, wobei zur besseren Übersicht alle bereits bekannten Parameter nicht mitgeschrieben werden.
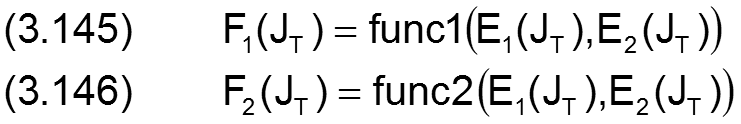
Damit ist ein nichtlineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten gegeben.
Für diese beiden Funktionen gibt es keinen analytischen Ausdruck. Es gibt lediglich ein Berechnungsverfahren gemäß den Abschnitten 3.4.1 bis 3.4.5, das für jeden Punkt des Definitionsbereichs die Funktionswerte berechnen kann.
Es ist nun in folgender Weise vorzugehen:
Zunächst sind für die gesuchten Werte E1(JT) und E2(JT) zwei Anfangswerte E1,0 und E2,0 festzulegen. Geeignete Anfangswerte können aus dem vorangegangen Verlagerungsverlauf extrapolierte Werte.
Für diese Anfangswerte können die Funktionswert F1,0 und F2,0 berechnet werden, die aber noch nicht mit F1(JT) und F2(JT) übereinstimmen.
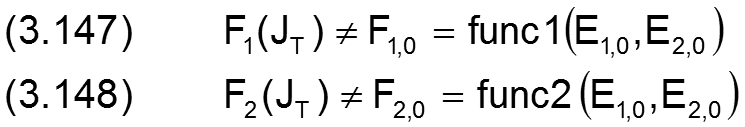
Nun sind verbesserte Werte E13 und E23 zu suchen, deren Funktionswerte F13 und F23 sich der vorgegebenen Lagerbelastung F1(JT) und F2(JT) weiter annähern
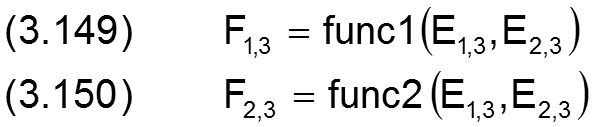
Als nächstes ist anhand vorgegebener Genauigkeitskriterien zu überprüfen, ob die Genauigkeit ausreichend ist und so die Iteration erfolgreich beendet werden kann. Siehe dazu Abschnitt 3.4.7.6.
Ist das nicht der Fall, sind die verbesserten Werte als neue Anfangsnäherungswerte zu setzen
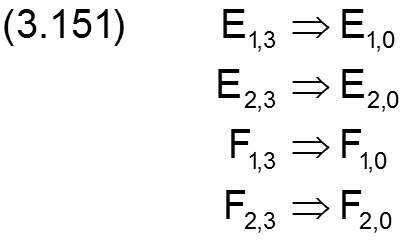
und ein erneuter Iterationszyklus auszuführen. Das ist zu wiederholen, bis die Genauigkeitskriterien erfüllt sind.
Da nicht jede Iteration zu einer Lösung konvergieren muss, wird zur Sicherheit die maximale Anzahl der zugelassenen Iterationszyklen auf einen Wert NJ begrenzt. Wenn bis dahin keine ausreichende Genauigkeit erzielt wurde, wird die Iteration abgebrochen und eine entsprechende Fehlermeldung ausgegeben.
Die Flussdiagramme in den Bildern 3.05 und 3.06 deuten diese Iterationsschleife (rote Schleife) in sehr vereinfachter Form an.
zurück weiterDie Suchstrategie wird hier beschrieben, mit welcher aus den Anfangsnäherungswerten E1,0(JT), E2,0(JT) die verbesserten Näherungswerte E1,3(JT), E2,3(JT) berechnet werden.
Kern des Problems ist die Formulierung einer zweckmäßigen Suchstrategie, die mit wenigen Berechnungen der Funktionen func1(E1...,E2...) und func2(E1...,E2...) auskommt, da sich hinter jeder Berechnung jeweils eine komplette Berechnung des Druckverlaufs P(Z,X) im Schmierspalt verbirgt.
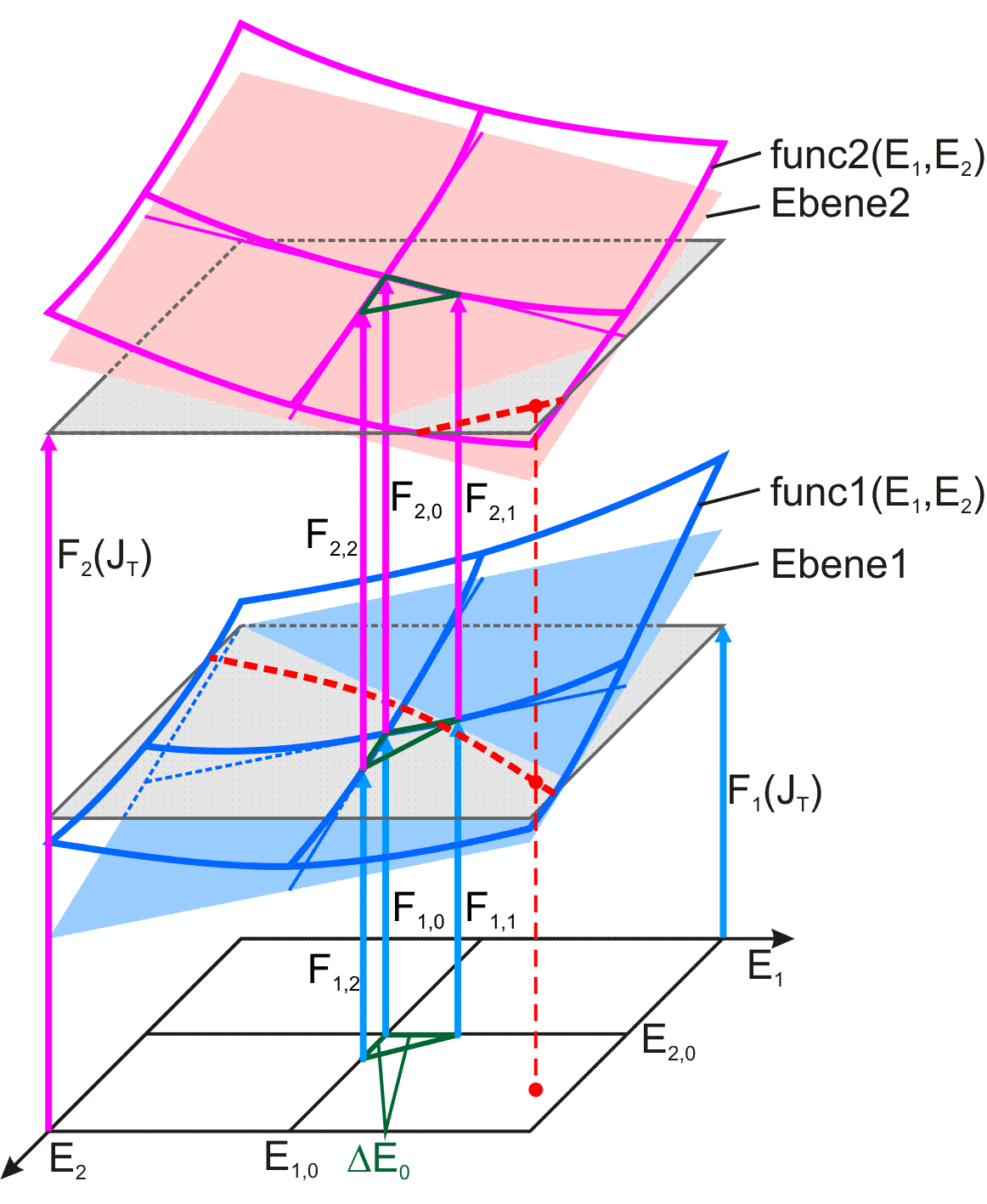
Bild 3.51: Skizzen der Funktionen func1 und func2 in der Umgebung der Anfangsnäherung E1,0, E2,0
Bild 3.51 skizziert die Funktionen func1 und func2 in der Umgebung der Anfangsnäherung [E1,0,E2,0] und dazu die Höhenebenen(in grauer Farbe) mit den Höhen F1(JT) und F2(JT). Die exakte Lösung liegt dort, wo die Funktion func1 die Höhenebene F1(JT) schneidet und gleichzeitig die Funktion func2 die Höhenebene F2(JT) schneidet, denn das ist die Lösung des nichtlinearen Gleichungssystems (3.145),(3.146)). Sowohl die Schnittlinien (gestrichelte rote Linien) der beiden Funktionen mit der entsprechenden Höhenebene, als auch der Kreuzungspunkt der Schnittlinien sind nicht direkt zu ermitteln. Deshalb werden beide Funktionen in der Umgebung der Anfangsnäherungslösung [E1,0;E2,0] durch die Ebenen 1 und 2 approximiert. Dazu werden die Funktionswerte der Funktionen func1 und func2 an je 2 weiteren Stellen ermittelt.
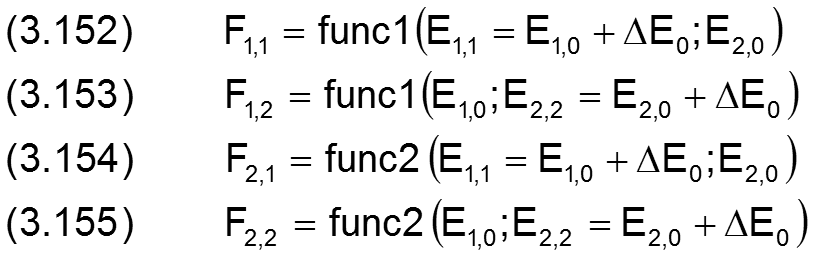
Mit den jeweils drei Stützstellen F1,0; F1,1; F1,2 und F2,0; F2,1; F2,2 können die Ebenen 1 und 2 aufgespannt werden. Je kleiner E0 gewählt wird, umso exakter bilden die beiden Ebenen die Tangentialebenen der beiden Funktionen im Punkt [E1,0;E2,0] ab. Mit Hilfe der tangentialen Ebenen 1 und 2 und den beiden Höhenebenen kann nun, sowohl grafisch als auch rechentechnisch, eine verbesserte Näherungslösung für das nichtlinearen Gleichungssystems (3.145),(3.146)) gefunden werden.
Bild 3.52 zeigt die grafische Lösung des Problems. Die verbesserte Näherungslösung [E1,3;E2,3] ist dann
![]()
![]()
mit
![]()
und
![]()
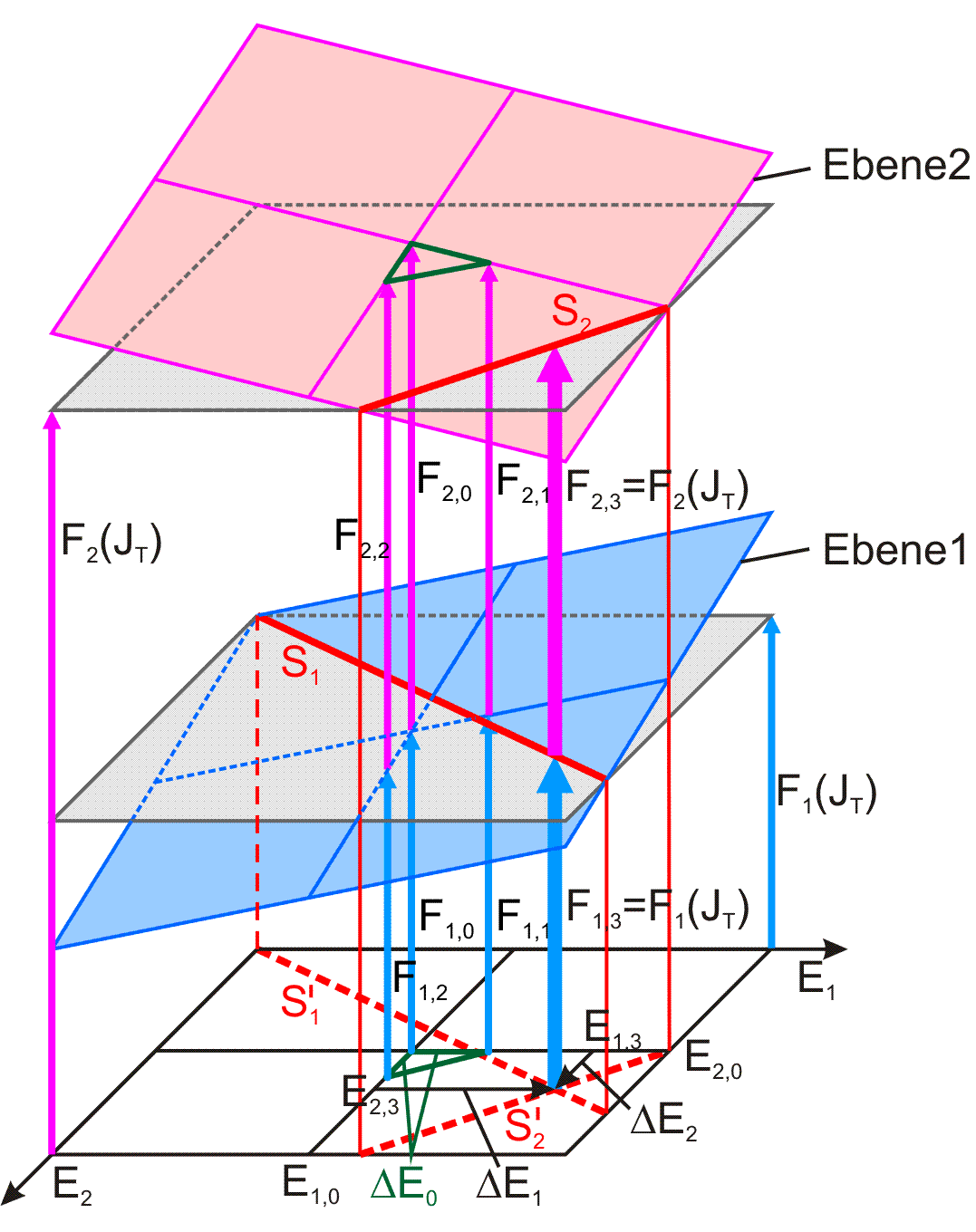
Bild 3.52: Darstellung der grafischen Lösung der Ermittlung eines verbesserten Wellenverlagerungspunktes [E1,E2]
Die Formeln zur nummerischen Lösung des Problems werden im folgenden Abschnitt angegeben.
zurück weiterAus der grafischen Lösung können nun leicht die Formeln für die numerische Lösung abgeleitet werden. Die Gleichungen für die tangentiale Ebene sind gegeben durch
Ebene2:
![]()
mit
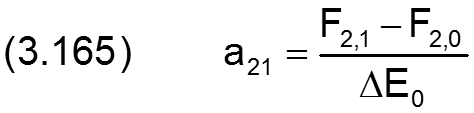
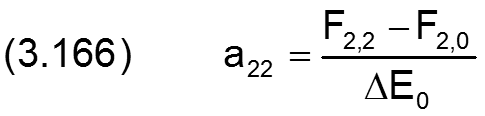
![]()
Die Schnittgeraden S1 und S2 der tangentialen Ebenen 1 und 2 mit den entsprechenden Höhenebenen F1(JT) und F2(JT) sind dann gegeben durch
![]()
![]()
Der Kreuzungspunkt der beiden Schnittgeraden ist dann gegeben durch
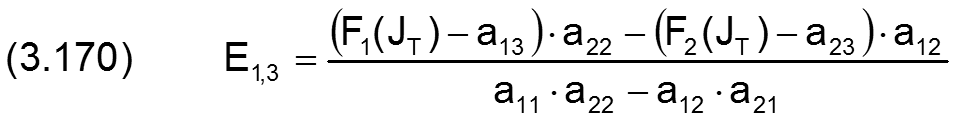
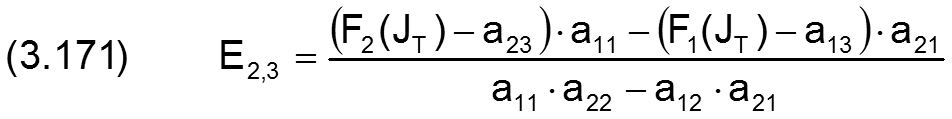
Der Wellenverlagerungspunkt [E1,3;E2,3] stellt die verbesserte Näherungslösung gegenüber der vorhergehenden Näherungslösung [E1,0;E2,0] dar.
In den vorhergehenden Abschnitten 3.4.7.1 bis 3.4.7.3 wurde davon ausgegangen, dass die Berechnung der Verlagerungsbahn in kartesischen Koordinaten E1(JT), E2(JT) erfolgt und dementsprechende Formeln angegeben. Das ist aber auch in den Polarkoordinaten E(JT), XE(JT) möglich. Der Ablauf und die erforderlichen Formeln sind prinzipiell gleich. Die unbekannten Variablen E1 und E2 müssen nur durch die neuen unbekannten Variablen E und XE ersetzt werden. Deshalb werden der Ablauf und die Formeln für polare Koordinaten hier nicht angegeben.
Prinzipiell funktionieren beide Verfahren in wesentlichen Bereichen des Lagerspiels gleich gut und dort ist es egal, welches Verfahren verwendet wird. Für beide Verfahren gibt es aber auch jeweils einen Bereich, wo das eine bzw. das andere Verfahren Probleme bekommt. Bild 3.53 zeigt 2 Beispiele, wo jeweils eine der beiden Iterationen Probleme hat.
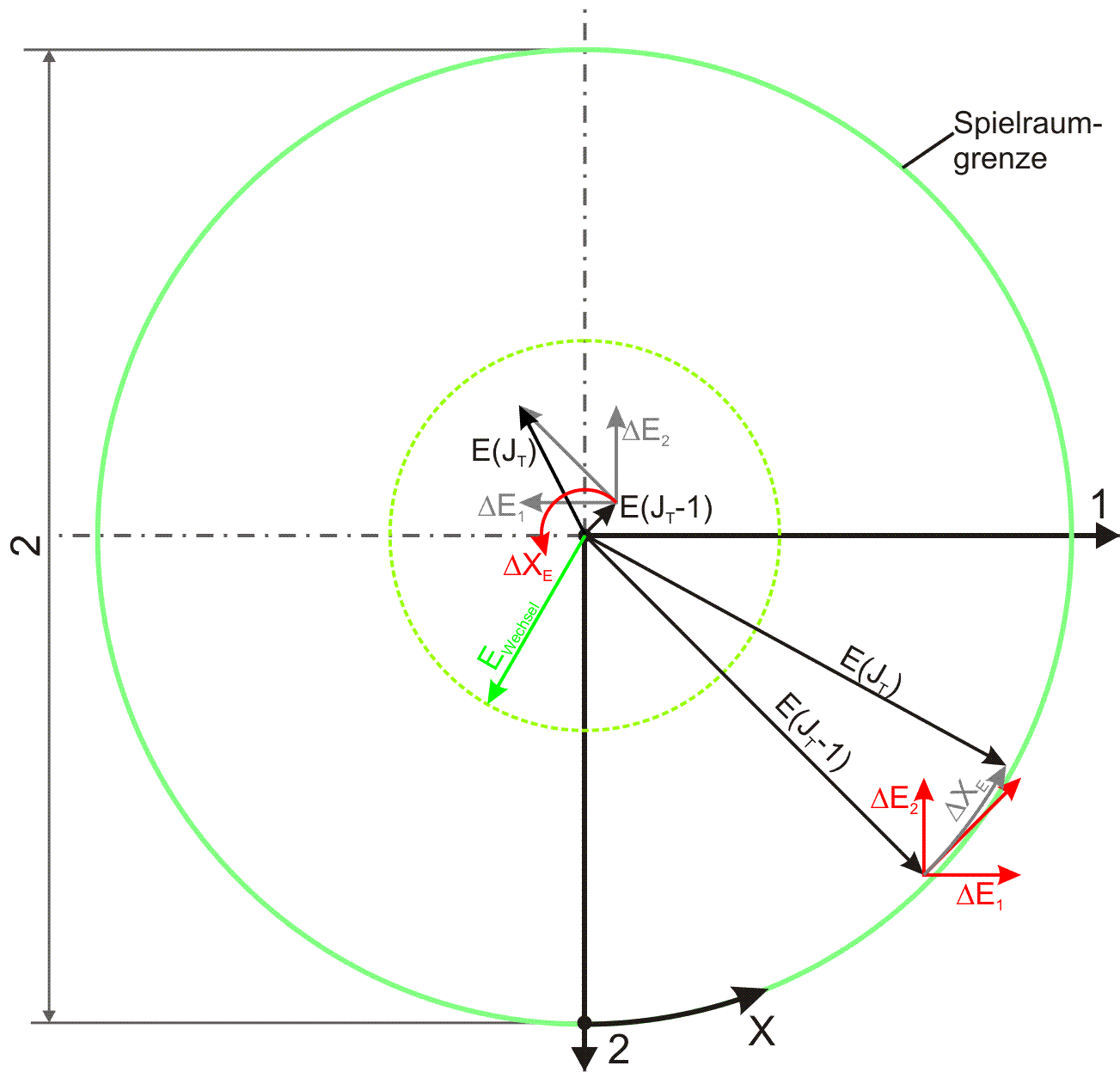
Bild 3.53: Zwei Beispiele mit problematischer Iteration in kartesischen bzw. polaren Koordinaten
Bei großer Exzentrizität und umlaufender Lagerbelastung, wo sich große ΔXE und sehr kleine ΔE ergeben, können mit polaren Koordinaten noch gute Ergebnisse erzielt werden, während mit kartesischen Koordinaten die Iteration nur in sehr kleinen Schritten vorankommt, da die Tendenz besteht, dass die Iteration den Definitionsbereich über die Spielraumgrenze verlässt.
Bei sehr kleiner Exzentrizität, nahe dem singulären Zentrum des Polarkoordinatensystems, kann die Iteration mit Polarkoordinaten leicht aus dem Tritt geraten und Unsinn rechnen, was auch zur Instabilität der Iteration und damit zum Abbruch der Berechnungen führen kann.
Deshalb werden in SIRIUS wahlweise das eine bzw. das andere Verfahren angewendet. Der Anwender braucht sich darum nicht zu kümmern. Die Auswahl erfolgt durch das Programm automatisch. Mit dem programminternen Parameter EWechsel (siehe Bild 3.53) ist eine Grenze festgelegt. Innerhalb dieses Grenzkreises arbeitet SIRIUS mit kartesischen Koordinaten und außerhalb mit Polarkoordinaten. Der Parameter EWechsel kann vorübergehend im Menü 4.4.12.3 "Programminterne Parameter bearbeiten" verändert werden. Die Iteration mit kartesischen Koordinaten ist in der Routine "Verlagerung1" programmiert und die Iteration mit Polarkoordinaten in der Routine "Verlagerung2". Während der Berechnung einer Verlagerungsbahn kann das Programm automatisch mehrfach zwischen diesen beiden Routinen wechseln.
zurück weiterIm Abschnitt 3.4.7.2 wurde beschrieben, wie an die Funktion So=func(E,XE) im Basispunkt [E0,XE0] die Tangentialebene angelegt wird, die als Approximation der Funktion im Bereich um E0 und XE0 dient und wie durch einen Schritt in Richtung E und XE ein verbesserter Näherungswert für E(JT) und XE(JT) gefunden wird. Bild 3.54 zeigt eine Skizze der Funktion So=func(E) quer durch den gesamten Spielraum des Lagers und die Tangente an die Funktion So=func(E) im Punkt E0.
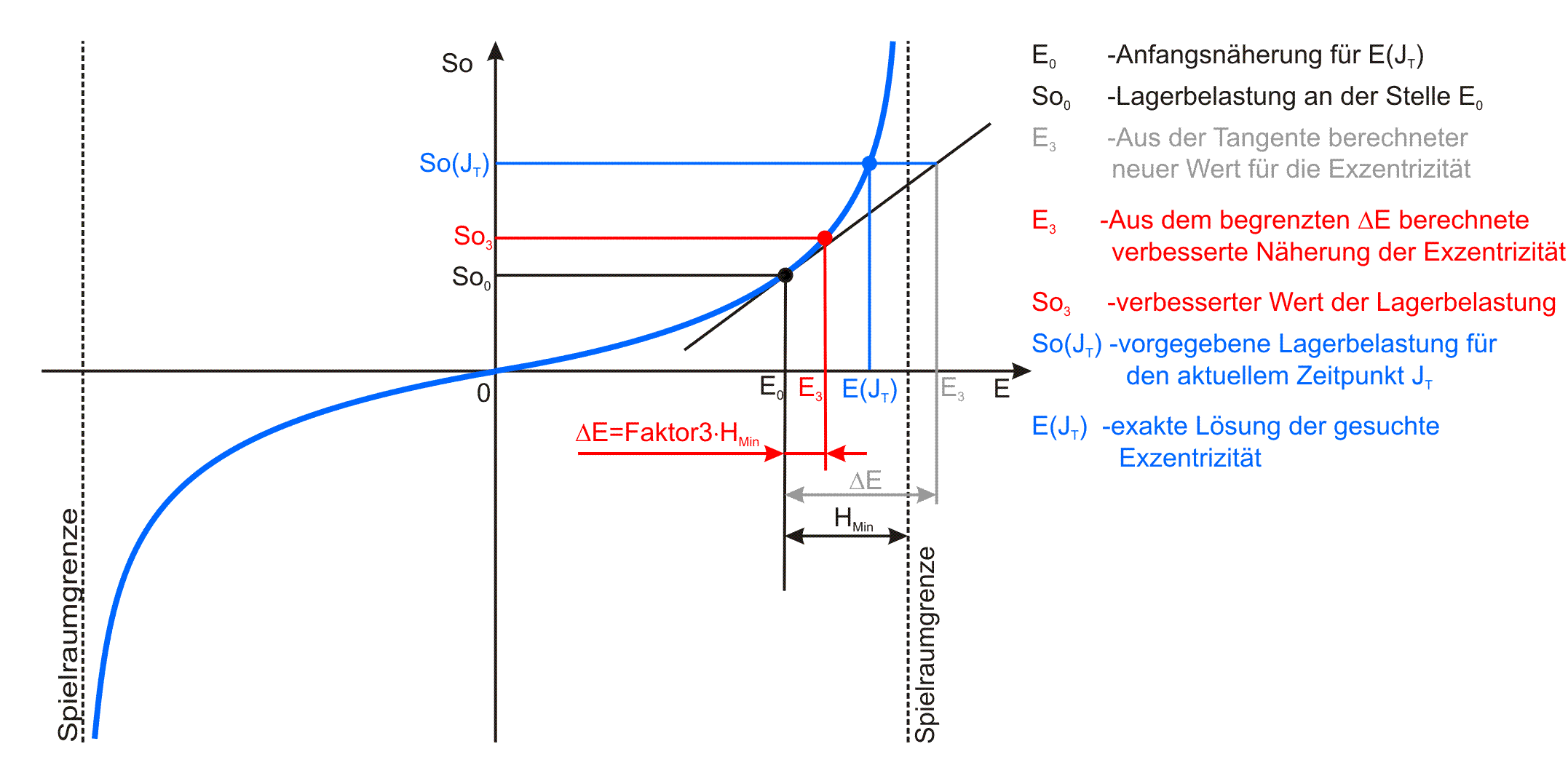
Bild 3.54: Skizze zur Begrenzung der Schrittweite ΔE
Da der Definitionsbereich der Funktion durch die Spielraumgrenzen begrenzt ist, kann die oben beschriebene Suchstrategie durch die Berechnung eines ΔE (grau dargestellt) aus dem Definitionsbereich herausführen. Das würde bedeuten, dass im nächsten Iterationsschritt eine Spalthöhe kleiner Null berechnet wird, was zum Abbruch der Berechnungen führt. Auch wenn ΔE so groß ist, dass die neue minimale Spalthöhe gerade noch größer Null ist, könnte sich das Ergebnis stark verschlechtern, weil mit HMin→0 So→∞ geht. Deshalb wurde eine Begrenzung für ΔE eingeführt, falls sich die Exzentrizität E der Spielraumgrenze nähert.
Das Kriterium lautet:
Wenn ΔE>Faktor3·HMin, dann wird ΔE=Faktor3·HMin gesetzt.
Ein geeigneter Faktor3 wurde empirisch ermittelt. Der Parameter Faktor3 kann im Untermenü: 4.4.12.3 "Programminterne Parameter bearbeiten" (im Hauptmenü: "Ende der Eingabe erreicht") zeitweilig geändert werden.
zurück weiterZu Berechnung der Wellenverlagerung aus einem vorgegebenen Lastverlauf werden pro Zeitpunkt JT maximal NJ Iterationen ausgeführt. Aktuell ist die Anzahl mit NJ=10 im Programm festgelegt. Dieser Wert kann im Untermenü: 4.4.12.3 "Programminterne Parameter bearbeiten" (im Hauptmenü: "Ende der Eingabe erreicht") zeitweilig geändert werden.
Sind nach diesen NJ Iterationen die geforderten Toleranzkriterien nicht erfüllt, wird die Berechnung erfolglos mit einer Fehlermeldung abgebrochen. Siehe dazu auch Abschnitt 4.9.2.3.
Für jeden zu berechnenden Zeitpunkt ist die erste Iteration eine Extrapolation. Aus der Wellenverlagerung E1(JT-1) und E2(JT-1) bzw. E(JT-1) und XE(JT-1) des vorhergehenden Zeitpunktes und deren Ableitungen ∂E1/∂T und ∂E2/∂T bzw. ∂E/∂T und ∂XE/∂T werden erste Näherungswerte E1,0 und E2,0 bzw. E0 und XE,0 für die Wellenverlagerung zum Zeitpunkt JT berechnet. Dann folgen je nach Bedarf maximal NJ-1 Iterationen, wie in den Abschnitten 3.4.7.2 bis 3.4.7.5 beschrieben.
Die ersten beiden Iterationen werden immer ausgeführt, unabhängig davon, wie genau das Ergebnis bereits ist. Beginnend nach der 2.Iteration wird anhand der Toleranzkriterien nach jeder Iteration geprüft, ob die Berechnung für den aktuellen Zeitpunkt erfolgreich beendet werden kann.
Für die Routine "Verlagerung1" wurden folgende 2 Toleranzkriterien festgelegt:
![]()
und
![]()
Für die Routine "Verlagerung2" wurden folgende 3 Toleranzkriterien festgelegt:
![]()
![]()
und
![]()
Für eine erfolgreiche Beendigung der Berechnung müssen jeweils alle 2 bzw. 3 Kriterien erfüllt sein.
Die Parameter TolE, TolXE und TolF können im Untermenü: 4.4.12.3 "Programminterne Parameter bearbeiten" (im Hauptmenü: "Ende der Eingabe erreicht") zeitweilig geändert werden.
Um den Verlauf der Iterationen verfolgen zu können, werden die Parameter ΔE1, ΔE2 und ΔF1, F2 in der Routine "Verlagerung1" bzw. ΔE, ΔXE, ΔF1 und ΔF2 in der Routine "Verlagerung2" für jeden Iterationsschritt angezeigt. Die Werte haben folgende Bedeutung:
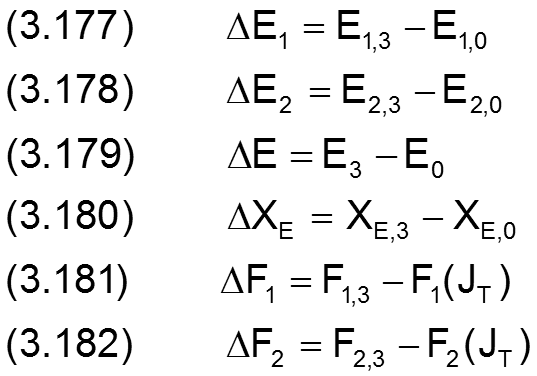
Die Bedeutung des jeweils 2.Indizes der Parameter ist im Bild 3.52 zu erkennen. Der Index 0 steht hier für den Näherungswert des jeweiligen Parameters vor dem Iterationsschritt und der Index 3 steht für den verbesserten Näherungswert des jeweiligen Parameters nach dem Iterationsschritt. Zu beachten ist hier, das die Werte ΔF1 und ΔF2 hier den tatsächlich noch vorhandenen Fehler zwischen dem vorgegebenen Soll-Wert und dem in der Berechnung realisierten Wert angeben, während die Werte ΔE1 und ΔE2 bzw. ΔE und ΔXE nur die letzte Verbesserung angeben. Der noch vorhandene Fehler zum exakten Wert kann also auch größer sein.
.
.
.