The optimization of the employment matrix ac leads to a linear optimization problem which can be solved with the simplex algorithm. General statements on the simplex algorithm can be found in Section 4.2.1 of Volume 1 [4].

We are looking for a maximum needs-conform performance structure db depending on the unknown variables ac_j2,j3 , which are the components of the employment matrix.

According to equation (10) for each component db_j3 of the needs-conform performance structure applies

The number a of workers and the normalized needs-based performance structure dbn are predetermined and cannot be influenced. In order to maximize db the factor fg which is contained in all m3 equations, has to be maximized.

Each of the m3 equations can therefore be used as a linear objective function because the only possible maximum for fg results in an overall maximum vector db according to these m3 equations. We take the first equation.

If one assumes that with an optimal employment matrix ac the performance vector d and the included needs-based performance vector db must be identical because no manpower can be wasted, then equation (5) can be inserted into the first equation. And so the linear objective function for the main problem is

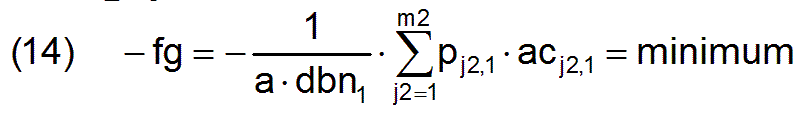
Now, by formulating suitable side conditions it must be ensured that the internal regularities associated with the employment matrix are also taken into account.

First of all, these are the m3-1 equations listed above which are not used as an objective function and therefore have to be entered in a different form as side conditions. They have an internal connection via the constant factor fg × a, which can also be written like this

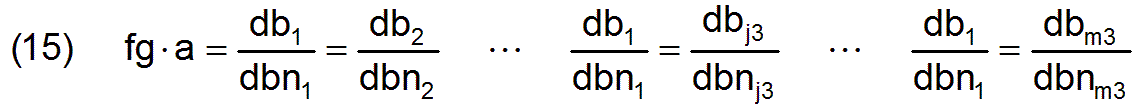
Equation (5) can also be inserted into the m3-1 equations. Accordingly, it can be formulated that for j3 = 2 to m3 applies

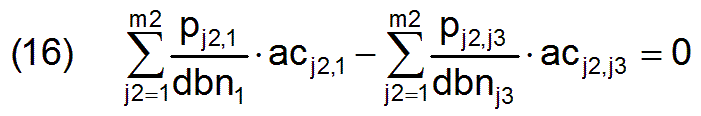
with which m3-1 side conditions are given.

The fact that the sizes ap_j2 of the productivity groups are given has to be taken into account by further m2 side conditions, so that for full employment applies

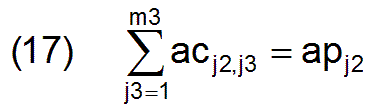
with which m2 further side conditions are given.

Thereby the optimization problem is already fully described. A simplex table which has m2 × m3 unknown variables, m2+m3-1 linear side conditions and one linear objective function can be written for the main problem. Since all side conditions are in non-canonical form, m2+m3-1 auxiliary variables have to be introduced and thus the auxiliary problem has to be solved first.

Then the main problem can be solved if the objective function of the auxiliary problem became zero. If the solution of the auxiliary objective function does not become zero, there is no solution to the main problem.

A TurboPascal program was written for the numerical solution of the optimization problem with the simplex algorithm, so that the numerical solution of the optimal employment structure can also be given for our demonstration example.