3 Mathematical description of an employment structure

Primary parameters:

There are a workers.
These workers are employed in m3 different professions, which are numbered with the index j3 .
It is assumed that the performance within a profession can be measured. Accordingly there can be a special unit of measurement or a normal Md_j3 for work performance for each profession.
A worker j1 has a certain individual skill for each profession j3 to achieve a corresponding productivity P_j1,j3 with normal effort. The totality of all productivities P_j1,j3 of a worker j1 results in a vector P_j1, which we call productivity profile. Usually every worker has its own individual productivity profile. To reduce the math we assume that there can be several workers with the same productivity profile. These workers are combined to form one productivity group.
Accordingly, the assumption is: There are m2 different productivity groups, which are numbered with the index j2. The productivity profile of group j2 is given by the productivity profile vector P_j2, which consists of the components P_j2,j3. The vectors P_j2 of the productivity groups can be combined into a matrix, which we call the matrix of productivity profiles or briefly the productivity matrix P of society.
The components P_j2,j3 of the productivity matrix P are made dimensionless with the corresponding normal_j3, so that there is the dimensionless productivity matrix p with the dimensionless components p_j2,j3.

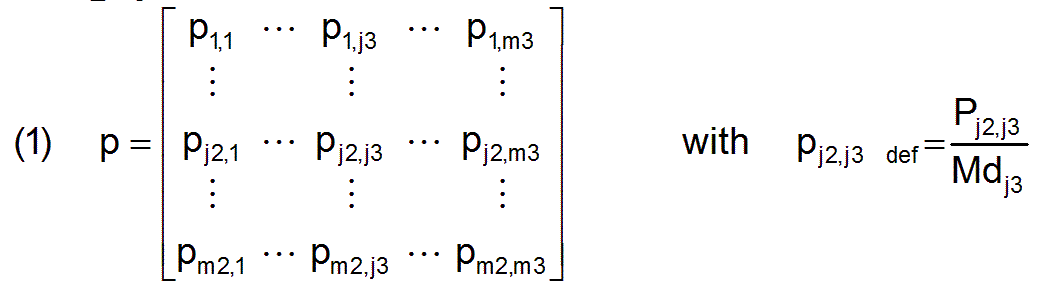
Each productivity group j2 includes ap_j2 workers who have the corresponding productivity profile. All these numbers can be summarized in a vector ap, which consists of the m2 components ap_j2 and which we call the vector of the productivity group sizes.

In fact, every worker has its own productivity profile. By introducing the productivity groups we have not made any significant restriction to the general case because if we set all productivity group sizes equal to one then again an individual productivity profile is given for each worker.

When assuming full employment the sum of all productivity group sizes is equal to the number a of workers.

The workers in a productivity group can be employed in different professions. For example, in profession j3 from productivity group j2 the number of ac_j2,j3 workers can be employed. This statement can be made for any productivity group and any profession. All numbers ac_j2,j3 for j2=1 to m2 and j3=1 to m3 result in a matrix ac with m2 rows and m3 columns which shall be called the employment matrix.

In the case of full employment applies

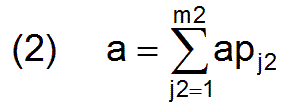
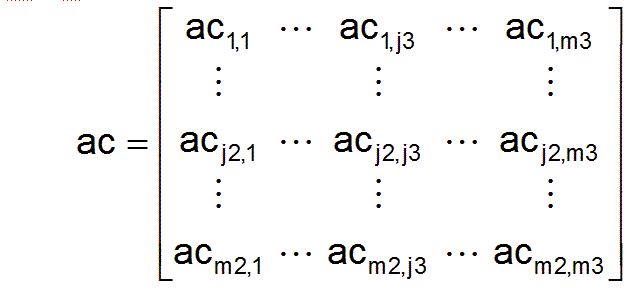
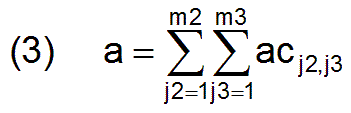
Now another vector shall be introduced as a test criterion for the needs-conformity of the employment structure.

Let us assume that there is a needs-based national economy in which every company can indicate the volume of employment it needs in each profession in order to provide its production. In order to supply this needs-based producing economy with needs-based and profession-specific work performance a needs-based performance structure can be specified by a vector db0 of a needs-based performance structure which components db0_j3 indicate for each profession j3 which profession-specific performance according to the profession's requirement must be provided.

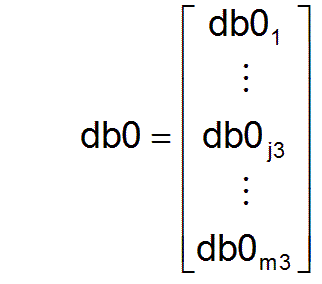
For the sake of simplicity in case of possible economic growth it is assumed that the proportions of the need for profession-specific performances will not change at short notice. This means that every multiple of this vector also results in a needs-based performance structure.

Thus all primary parameters for describing an employment structure have been introduced.

Secondary parameters:

All secondary parameters can be derived from the primary ones. They serve to make it easier to evaluate the later results of an optimization.

For each profession j3 the normalized productivity pn_j3 is defined by

This value can be interpreted as the mean productivity of all workers, including those who do not work in this profession. These values would also result in the mean productivity of all workers employed in the profession if the number of workers is very large and the distribution of workers among the respective professions were completely left to chance and their respective skills are not taken into account at all. Thus _j3 is also the profession-independent mean productivity of the workers in the entire society. This can be seen as a constant value over time and should serve as a base value to show how actual productivity can be increased by optimizing the employment matrix.

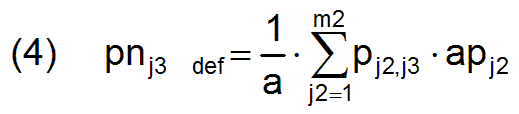
The m3 parameters pn_j3 are combined to a vector pn, which represents the normalized, profession-independent productivity profile of society.

Using the employment matrix ac and the productivity matrix p, for each profession can be calculated j3 which work performance d_j3 is currently achieved in this profession.

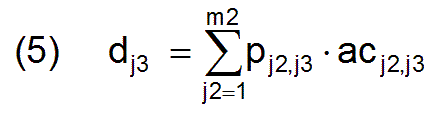
The vector d, consisting of the m3 components d_j3, results in the structure of the work performance that is currently done due to the current employment matrix ac.

The current numbers ae_j3 of workers who are employed in the respective profession j3 are calculated from the employment matrix ac by

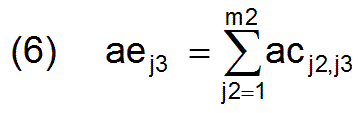
They are combined in the vector ae

For each profession the mean productivity pm_j3 is defined j3 by

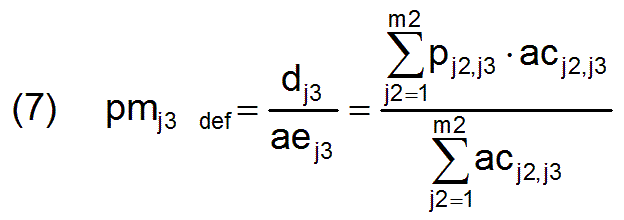
Thus pm_j3 is the mean productivity of the workers actually employed in this profession, which means it is profession-dependent. (Compare indicative value pm with indicative value pn)

The m3 parameters pm_j3 are combined to form a vector pm which represents the mean profession-dependent productivity profile of society. With this vector the "societally necessary working time" for a product is given in the Marxian sense.

The ratio between the mean profession-dependent productivity pm_j3 and the normalized (mean profession-independent) productivity pn_j3 results in the factor fp_j3 for the increase of productivity in the respective profession j3.

(8) fp_j3 _def= pm_j3/pn_j3

As not every profession requires workers from all productivity groups a reasonable employment policy can ensure that the most productive people work within each professional field. The factors fp_j3 provide information on the extent to which productivity increases in society are achieved just by employment policy, and thus represent quality criteria of employment policy.

The vector db0 is initially given arbitrarily with regard to the level of its components, since at the moment only the relationships of the components to one another are important for the description of a needs-based performance structure. This vector is normalized by introducing a vector dbn for a normalized, needs-based performance structure.

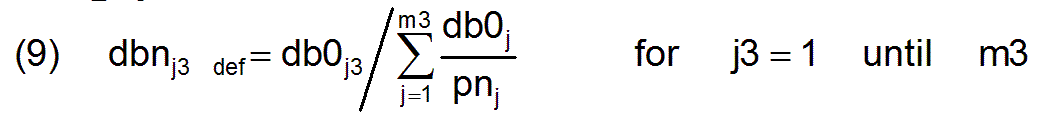
Since the value of the denominator in this formula is constant in relation to the index j3, it is obvious that the vector dbn represents a multiple (or a fraction) of the vector db0 and is therefore also a needs-based performance structure. In addition, the vector dbn corresponds to the performance structure of a needs-based producing society that consists only of one "normal" worker, whose individual productivity profile is pn.

The vector d of the current societal performance structure due to the employment matrix ac does not have to be needs-based. The largest vector it contains which represents a needs-based performance structure is referred to as db. db is then the largest vector of a needs-based performance-oriented structure that is contained in vector d, if for all db_j3 with j3= 1 to m3 the following applies:

(10) db_j3 = fg × a ×dbn_j3

where for all applies db_j3 £ d_j3 and for at least one j3 applies db_j3 = d_j3 .

Hereby the factor fg was introduced as well. It represents the factor of increased overall societal performance due to the employment matrix ac. It is the most important parameter for evaluating the quality of the employment matrix. Therefore it is used as an objective function of an optimization calculation later on.

The factors fb_j3 for evaluating the needs-conformity of the work performances can be defined by

(11) fb_j3 _def= db_j3 / d_j3

Accordingly, for each profession they indicate how large the share of needs-based work is in relation to the total work performed in the respective profession. The aim for all fb_j3 is to have the value one, because then work is carried out completely needs-based ably.

From these factors the more complex factor fbg can be specified. It provides a quick overview of the needs-conformity of overall societal work performance.

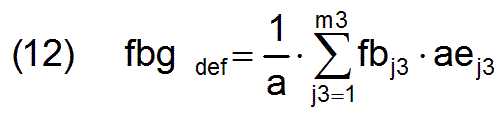
If fbg=1, then in total work is done according to needs. The factor indicates what proportion of workers is involved in the overall societal needs-conform work performance structure db within the possibly non-needs-conform work performance structure d.

Return Go on