Die Optimierung der Beschäftigungsmatrix ac führt auf ein lineares Optimierungsproblem, welches mit dem Simplexverfahren gelöst werden kann. Zu allgemeinen Aussagen zum Simplexalgorithmus wird auf Abschnitt 4.2.1 des Bandes 1 [4] verwiesen.

Gesucht ist also eine maximale bedarfsgerechte Leistungsstruktur db in Abhängigkeit von den unbekannten Variablen ac_j2,j3 ,den Komponenten der Beschäftigungsmatrix.

Für jede Komponente db_j3 der bedarfsgerechten Leistungsstruktur gilt gemäß Gleichung (10)

Die Anzahl a der Arbeiter und die normierte bedarfsgerechte Leistungsstruktur dbn sind vorgegeben und können nicht beeinflußt werden. Um db zu maximieren muß also der Faktor fg maximiert werden, der in allen m3 Gleichungen enthalten ist.

Jede der m3 Gleichungen kann demnach als lineare Zielfunktion verwendet werden, denn bei dem einen für fg möglichen Maximum ergibt sich nach diesen m3 Gleichungen ein insgesamt maximaler Vektor db. Wir nehmen die erste Gleichung.

Wenn man davon ausgeht, daß bei einer optimalen Beschäftigungsmatrix ac der Leistungsvektor d und der darin enthaltene bedarfsgerechte Leistungsvektor db identisch sein müssen, weil keine Arbeitskraft vergeudet werden darf, kann in die erste Gleichung die Gleichung (5) eingesetzt werden. und so lautet die lineare Zielfunktion für das Hauptproblem

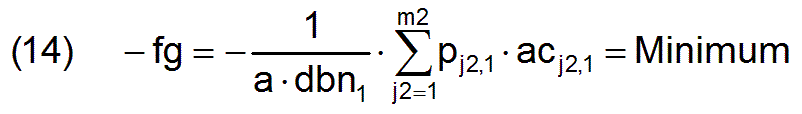
Nun muß noch durch Formulierung geeigneter Nebenbedingungen dafür gesorgt werden, daß die inneren Gesetzmäßigkeiten, die mit der Beschäftigungsmatrix zusammenhängen, außerdem berücksichtigt werden.

Das sind zunächst die m3-1 oben angeführten Gleichungen, die nicht als Zielfunktion verwendet werden und deshalb in anderer Form als Nebenbedingung eingehen müssen. Diese haben über den konstanten Faktor fg × a einen inneren Zusammenhang, der auch so geschrieben werden kann

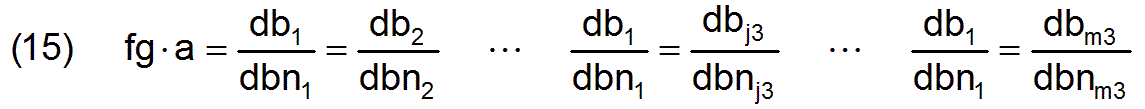
In die m3-1 Gleichungen kann ebenfalls die Gleichung (5) eingesetzt werden. Dementsprechend kann formuliert werden, für j3= 2 bis m3 gilt

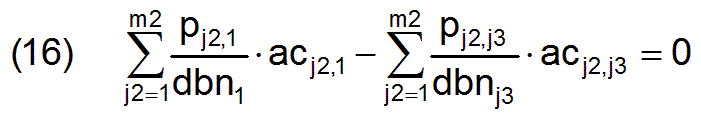
womit m3 -1 Nebenbedingungen gegeben sind.

Als weitere m2 Nebenbedingungen ist die Tatsache zu berücksichtigen, daß die Größen ap_j2 der Produktivitätsgruppen vorgegeben sind, so daß bei Vollbeschäftigung gilt

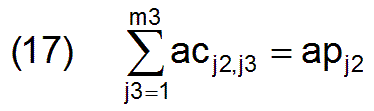
womit m2 weitere Nebenbedingungen gegeben sind.

Damit ist das Optimierungsproblem bereits vollständig beschrieben. Es kann ein Simplextableau geschrieben werden, welches m2 × m3 unbekannte Variable hat, m2+m3-1 lineare Nebenbedingungen und eine lineare Zielfunktion für das Hauptproblem. Da alle Nebenbedingungen in nicht kanonischer Form vorliegen, sind m2+m3-1 Hilfsvariable einzuführen und damit zunächst das Hilfsproblem zu lösen.

Anschließend kann das Hauptproblem gelöst werden, falls die Zielfunktion des Hilfsproblems Null wurde. Wenn die Lösung der Hilfszielfunktion nicht Null wird, gibt es keine Lösung für das Hauptproblem.

Für die numerische Lösung des Optimierungsproblems mit dem Simplexalgorithmus wurde ein TurboPascal-Programm geschrieben, so daß für unser Demonstrationsbeispiel auch die zahlenmäßige Lösung der optimalen Beschäftigungsstruktur angegeben werden kann.