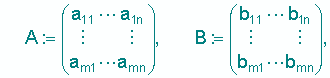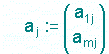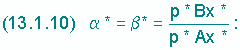zurück   weiter

8 Vorläufige Literaturauswertung

Übliche Verfahrensweise der Modellierung einer ganzen Volkswirtschaft ist das Sektorenmodell der Makroökonomik, in der die verschiedenen Elemente einer Volkswirtschaft in Sektoren zusammen gefasst werden. Dabei werden alle Waren zum Sozialprodukt zusammen gefasst (aggregiert) und alle Unternehmen zu einem Ein-Waren-Produzenten. Erst danach, wenn bereits wesentliche Untersuchungsmöglichkeiten durch diese Abstraktion von vornherein unmöglich gemacht sind, beginnen die eigentlichen Untersuchungen. Den Grund dafür sehe ich u.a. in der ideologisch begründeten starken Fixierung der Protagonisten der kapitalistischen Marktwirtschaft auf die Untersuchung von Wertbeziehungen, so dass ihnen der dahinter stehende materiell-technische volkswirtschaftliche Reproduktionsprozess nicht mehr wichtig genug erscheint. Der Glaube an eine spontan wirkende Wertfunktion, die alle Waren vergleichbar machen soll, verleitet zu dieser vorschnellen Abstraktion. Dabei werden zwar gelegentlich auch einige halbherzige Unterteilungen des Sektors der Produzenten vorgenommen, die aber nichts wesentlich neues bringen. Anschließend werden intuitiv funktionelle Beziehungen zwischen den verschiedenen nur noch Werte repräsentierenden aggregierten Größen erzeugt, um damit ein gesamtwirtschaftliches Gleichgewicht nachzuweisen, welches je nach Vertreter einer Richtung bei Vollbeschäftigung oder bei Teilbeschäftigung liegen soll.

Dieses unbefriedigende Bild stellte sich mir nach meinen ersten, natürlich nicht umfassenden Literaturstudien der Volkswirtschaftslehre zu Beginn meiner Untersuchungen dar. Als Ossi, der bis dahin zu diesem Thema im wesentlichen das Kapital von Marx [10] gelesen hatte, habe ich eigentlich gehofft, von Wissenschaftlern, die sich professionell mit ihrem eigenen System befassen und frei von Gängelei ihrer Landesfürsten forschen dürfen, etwas mehr substantiellen Informationsgewinn über die Marktwirtschaft zu erhalten.

Daraufhin habe ich mich erst mal nicht weiter um die Literatur gekümmert und meine eigenen Untersuchungen angestellt, natürlich stark beeinflusst von meiner bisher informativsten Literaturquelle in Sachen Marktwirtschaft, dem Marxismus.

Nachdem ich mit meinen Untersuchungen schon weit vorangekommen war und in der Literatur noch einmal gezielt nach vergleichbaren Ansätzen suchte, fand ich unter ferner liefen innerhalb der Wachstumstheorie das von-Neumann-Modell, welches dem von mir gewählten Ansatz entspricht. Zum Vergleich mit meinen Untersuchungen werde ich es deshalb hier einschließlich einiger Erweiterungen dokumentieren und kommentieren.

Bereits 1937 macht John von Neumann [14] einen Modellansatz zur Beschreibung einer Marktwirtschaft, indem er auf die übliche Aggregation von Waren und Produzenten verzichtet. Typisch für die Geringschätzung dieses Ansatzes ist die Behandlung in dem 600-seitigen Lehrbuch der Volkswirtschaftslehre von Samuelson [17]. In seinem 40-seitigen Kapitel über die Wachstumstheorie erledigt er dieses Modell auf reichlich einer halben Seite, die ich hier wegen ihrer Kürze vollständig wiedergeben kann:

"Das expandierende Universum: ein Exkurs

Der verstorbene John von Neumann, ein brillanter Mathematiker, der mit zum Bau der Wasserstoffbombe beitrug und die Spieltheorie begründete, erstellte ein Wirtschaftsmodell, in dem jedes Produkt aus jedem anderen hergestellt werden kann. Wenn der Boden und die Arbeit oder die Arbeit allein nicht mehr knappe limitierende Faktoren sind, dann hat das Gesetz abnehmender Grenzerträge keine Gültigkeit mehr. Alle Früchte der Produktion, die über die Kosten der Erhaltung von Pferden, Kaninchen, Webstühlen und komfortabel lebenden Menschen hinausgehen, werden in dem System wieder investiert, um mehr Pferde, Kaninchen, Webstühle und Menschen entstehen zu lassen.

In diesem System, das dem paradiesischen Zeitalter von Smith bis auf die Tatsache entspricht, dass es ausdrücklich Kapitalgüter mit einbezieht, gibt es ein maximales gleichgewichtiges Wachstum. Und es stellt sich heraus, dass diese Wachstumsrate - wir wollen sie wegen ihrer Ähnlichkeit mit Harrods natürlicher Wachstumsrate g nennen - genau gleich dem Zinssatz i ist.

Da die Entwicklungstheorie sich für Länder, wie zum Beispiel Indien und die Vereinigten Staaten, vorrangig mit dem Begriff des "gleichgewichtigen Wachstums" beschäftigt, ist das Neumann-Modell von beachtlichem Interesse. Es ist besonders relevant für den Fall, wo ein industrieller Sektor in einem armen Land auf ein unbegrenztes Arbeitsangebot im Agrarsektor zum konstanten Subsistenzlohn zurückgreifen kann. Da er wenig Boden benötigt, kann der industrielle Sektor den "take-off" vollziehen und mit konstanter Neumann-Rate jährlich wachsen, vorausgesetzt, er kann genügend Kapitalgüter zur Beschäftigung der zusätzlichen Arbeiter erzeugen oder Hilfe durch Importe von Seiten ausländischer Kreditgeber, Hilfsorganisationen oder Exporteure finden, falls er gewillt ist, eine solche zu suchen.

Falls technischer Fortschritt vorhanden ist, kann das System mit einer noch höheren als der Neumann-Rate wachsen. Wenn es dem System gelingt, sozusagen neue Erfindungen zu produzieren, welche die Effizienz des Arbeitseinsatzes mit einer konstanten Rate steigern, dann wird der Betrachter in der Tat erkennen, dass es zu einem noch schnelleren Neumann-Wachstum fähig ist.

Ein ganz einfaches Beispiel für ein expandierendes System wäre der Fall von Kaninchen (oder Menschen), die 1,05 Kaninchen pro eingesetztem Kaninchen erzeugen. Zinssatz und Wachstumsrate sind dann offensichtlich fünf Prozent pro Periode. Andere Beispiele sind nicht ganz so einfach."

Dieses Zitat demonstriert, wie man unter einem Deckmäntelchen scheinbar wissenschaftlich objektiver Berichterstattung über sonstige Theorien z.B. durch die Wahl der Beispiele, in diesem Fall der Kaninchen, die in dem Ruf stehen sich explosionsartig zu vermehren, eine Theorie diskreditieren. Das vorangestellte Lob, dass der Autor ein brillanter Mathematiker war, dient nur dazu sich zunächst die Aura eines unvoreingenommenen Berichterstatters zu geben, um später unbekümmert vom Leder zu ziehen. Außerdem ist damit gleich zum Ausdruck gebracht, dass es sich hier nicht um einen Wirtschaftswissenschaftler handelt, der den Unsinn verzapft hat. Man ist offenbar nicht gewillt, von seinen liebgewonnen eigenen Vorstellungen zulassen und ernsthaft über das Erkenntnispotential alternativer Ansätze nachzudenken.

Dieser Ansatz wurde aber auch von einigen Autoren aufgegriffen und weiterentwickelt. Sowohl das von-Neumann-Modell als auch die wesentlichen Erweiterungen wurden in dem Buch "Theorie des wirtschaftlichen Wachstums" von Krelle[7] in kurzer und übersichtlicher Form dargestellt. Da diese gut geeignet ist, dem Leser die Übereinstimmungen und die Unterschiede zu meinen Untersuchungen zu veranschaulichen, soll diese Darstellung hier ebenfalls fast vollständig wiedergegeben werden, wobei die enthaltenen Beweise und Ableitungen weggelassen werden:

"1.3.1 Von Neumann - Wachstumsmodelle

13.1.1 Das ursprüngliche v.-Neumann-Modell mit der Erweiterung von Kemeny, Morgenstern und Thompson

Von Neumann [1937] hat in einem Seminar ein Wachstumsmodell vorgestellt, das , nachdem die Arbeit ins Englische übersetzt worden war [1945/46], vielfach aufgegriffen und weiterentwickelt wurde. Wir bringen es hier in der (abgeänderten) Form von Kemeny, Morgenstern und Thompson [1956] und weisen dann auf eine Erweiterung durch Karlin [1959] und insbesondere auf die wichtige Erweiterung durch Morishima [1969] hin. Weitere Einzelheiten sind z.B. zu entnehmen aus: Gale [1960], Nikaido [1968], Moeschlin [1974] sowie aus Lehrbüchern über Mathematische Wirtschaftstheorie und über Wachstumstheorie, z.B. Takayama [1974], Kap.6, Burmeister und Dobell [1970], Kap.7, oder Krelle und Gabisch [1972], Kap.VIII. Natürlich gibt es auch eine Fülle von Artikeln hierzu.

Die grundlegenden Annahmen sind folgende. Es gebe m Güter in der Volkswirtschaft. Jedes von ihnen wird in einer Produktionsperiode durch den Einsatz dieser m Güter oder einer Untermenge von ihnen produziert. Die zur Produktion eines Gutes notwendigen Güter müssen also in der Vorperiode produziert werden und am Ende der Vorperiode voll zur Verfügung stehen, und sie werden in der Produktionsperiode voll verbraucht. Es gibt also keine längerlebigen Investitionsgüter. Die Güter sind auch nicht lagerfähig: was in der nächsten Periode benötigt wird, muss in der Vorperiode erzeugt werden.

Für die Produktion der m Güter stehen n Produktionsprozesse zur Verfügung. Jeder Produktionsprozess j lässt sich durch fixe Inputkoeffizienten aij ³ 0 und Outputkoeffizienten bij ³ 0 beschreiben, i=1,...,m, j=1,...,n. Die Inputkoeffizienten a1j,...,amj für den Prozess j geben an, welche Menge Güter 1,...,m man an Input benötigt, um den Produktionsprozess j während einer Periode auf einem beliebig definierten Niveau, hier Intensität genannt, durchführen zu können. Das Ergebnis ist ein Output b1j,...,bmj der Güter 1,...,m.

Die im Zeitverlauf konstante Technologie lässt sich also durch die Matrix A der Inputkoeffizienten und die Matrix b der Outputkoeffizienten darstellen:

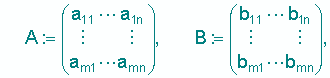
Hier sollten jetzt die Definitionen A und B erscheinen!

wobei jede zusammengehörige Spalte von A und B ein Produktionsverfahren charakterisiert.

Da es kein Output ohne Input gibt, muss jeder Spaltenvektor

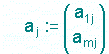
Hier sollte jetzt die Definitin aj erscheinen!

mindestens ein positives Element enthalten. Da jedes Gut produziert werden muss, muss jeder Zeilenvektor bi := (bi1 ... bin) zumindest ein positives Element enthalten.

Jeder Produktionsprozess j kann auf einem beliebigen Niveau (oder: mit einer beliebigen Intensität xj ³ 0 betrieben werden; man benötigt dazu aijxj Inputs und erhält entsprechend bijxj Outputs.

Man betrachtet proportionales Wachstum aller Outputs, d.h. alle Intensitäten xj wachsen mit der gleichen Rate w:

xjt = a × xj,t-1 ,a = 1 + w , a = Wachstumsfaktor.

Jedes Produkt i hat einen Preis pi , der sich im Zeitverlauf nicht ändert. Die Unternehmen müssen die Inputs zu diesen Preisen kaufen und das hierfür benötigte Kapital zu einem bei allen Produktionsprozessen gleichen Zinssatz z (gerechnet auf die Produktionsperiode) verzinsen. Wir definieren:

b = 1 + z , b = Zinsfaktor .

Die Mittel zur Verzinsung des Kapitals erhalten die Unternehmen aus dem Verkauf ihrer Produkte.

Es soll vollständige Konkurrenz auf allen Märkten herrschen, so dass die Prozesse, die benutzt werden, gerade die Inputkosten (einschließlich der Verzinsung) decken, während alle nicht benutzten Prozesse nur Verluste bringen würden. Abfallprodukte (das sind solche, die mit größeren Mengen anfallen als sie in der nächsten Periode benötigt werden) haben den Preis Null.

Die Prozessintensität xj werden zu einem Spaltenvektor x:=(x1 ...xn)’, die Preise pi zu einem Spaltenvektor p:=(p1 ...Pm)’ zusammengefasst.

Soweit der allgemeine Ansatz. Er wird in den folgenden sogenannten "Axiomen" präzisiert - das sind in Wirklichkeit die Gleichgewichtsbedingungen dieser Ökonomie.

Axiom 1 (Technische Durchführbarkeit der Produktion):

a × Ax £ Bx

Die in der Vorperiode erzeugten Mengen Bx von jedem Gut müssen ausreichend, um den Input für die nächste Periode zu liefern, wobei in der nächsten Periode jede Intensität um den Wachstumsfaktor a erhöht wird.

Axiom 2 (Kein reiner Unternehmergewinn bei den betriebenen Prozessen; bei den nicht betriebenen Prozessen können Verluste eintreten):

p’ B £ b × p’A

p’ B ist der Zeilenvektor der Erlöse aus jedem Prozess bei Betreibung auf Einheitsniveau. b × p’ A ist der Zeilenvektor der Kosten der Betreibung jedes Prozesses auf Einheitsniveau, einschließlich der Zinskosten.

Axiom 3 (Preis Null von Abfallprodukten]:

p’ Bx = a p’ Ax

p’ Bx ist der Gesamterlös aus allen Produktionsprozessen der Vorperiode, a p’ Ax ist der Wert des Faktoreinsatzes bei allem Produktionsprozessen in der nächsten Periode. Da nach Axiom 1 Bx ³ a × Ax, muss der Vektor p an den Stellen i ein Nullelement haben, wo in der Zeile i von Bx ³ a Ax ein striktes Ungleichheitszeichen steht; d.h. der Preis des Gutes i, das (als Kuppelprodukt) im Überfluss produziert wird, ist Null.

Axiom 4 (Unrentable Prozesse werden nicht benutzt):

p’ Bx = b × p’ Ax

p’ Bx ist wieder der Gesamterlös aus der Produktion der Vorperiode, b × p’ Ax sind die Gesamtkosten der Vorperiode, einschließlich Zinskosten, Dies impliziert zusammen mit Axiom 2, dass diejenigen Prozessniveaus xj Null sind, bei denen in p’B £ b × p’ A ein striktes Ungleichheitszeichen steht; dies sind die unrentablen Prozesse.

Axiom 5 (Positiver Wert der Gesamtproduktion):

p’ Bx > 0

Hier wird gefordert, dass nicht nur Abfallprodukte erzeugt werden und dass die trivialen Nullösungen x=0, p=0 ausscheiden.

Wie bereits gesagt, muss natürlich A ³ 0, B ³ 0 sein, und jeder Spaltenvektor von A und jeder Zeilenvektor von B muss mindestens ein positives Element enthalten.

Ein von Neumann - Wachstumspfad (oder: von Neumann - Gleichgewicht) ist nun ein Quadrupel (a ,b ,x,p), das den Axiomen 1-5 genügt. Von Neumann bewies die Existenz mit einem von ihm hierzu erweiterten Fixpunktsatz. Es gibt andere Beweise. Krelle und Gabisch [1972] folgen einem Beweis von Howe [1960] und Nikaido [1968]. Diese Beweise sind relativ lang und umständlich. Wir geben daher einen spieltheoretischen Beweis, entlang den Linien von Kemeny, Morgenstern und Thompson [1956] und Moeschlin [1974]; er ist kürzer und einfacher."

Der folgende Beweis wird hier weggelassen und es geht weiter mit Schussfolgerungen und Bewertungen. Im darauf folgenden Kapitel 13.1.2 wird dann eine Weiterentwicklung von Morishima dargestellt:

"Zwischen a * , b *, x* und p* besteht nach den Axiomen 3 und 4 die Beziehung

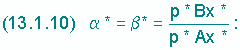
Zins- und Wachstumsfaktor sind gleich dem Quotienten von Outputwert und Inputwert bei der Produktion.

Die a *, b *, x* und p* lassen sich durch Programmierungsverfahren oder andere Methoden auch numerisch bestimmen; vgl. hierzu z.B. Moeschlin [1974], S.37 ff. oder Künzi, Krelle, v. Randow [1979], S.67 ff.

Das Ergebnis ist also, dass es eine maximale Wachstumsrate gibt, mit der eine Wirtschaft dieser Art wachsen kann, und dass diese Wachstumsrate gleich der Zinsrate ist.

Alle Sektoren wachsen mit dieser Rate, und alle Preise und Produktionsintensitäten sind als Funktion dieser Wachstumsrate eindeutig bestimmt.

Dies ist interessant und wichtig, allerdings nur insoweit relevant, als die von Neumannsche Modellwirtschaft die Realität einigermaßen richtig wiedergibt. Das trifft allerdings nicht zu. Es fehlt der technische Fortschritt. Vor allem fehlt der Endkonsum. Alle für die Produktion notwendigen Faktoren, also auch die Arbeit, werden in diesem Modell produziert. Menschen werden sozusagen wie das Vieh betrachtet; sie erhalten die notwendigen Nahrungsmittel usw. als Input, damit sie Arbeit leisten können. Von der Mehrproduktion hat am Ende niemand etwas, außer, dass auch mehr Menschen gleichlaufend erzeugt werden. Es gibt keinen steigenden Lebensstandard, vielmehr werden alle produzierten Güter sofort zur Produktion von mehr Gütern wieder eingesetzt. Die von Neumannsche Wachstumsrate ist daher die maximale Wachstumsrate, die eine Wirtschaft erreichen kann. Normalerweise wird sie, weil es ja einen Endkonsum (also eine "Verschwendung" im Sinne des von Neumannschen Wachstumsmodells) gibt, ziemlich weit dahinter zurückbleiben.

Dagegen sollte man das Fehlen längerlebiger Kapitalgüter und die für alle Güter einheitliche Produktionsperiode nicht kritisieren. Diese Annahmen kann man durch Definition von gebrauchten Maschinen und Halbfertigwaren als Produkte stets erfüllen.

Diese Kritikpunkte wurden zum Teil beseitigt durch die Erweiterung des von Neumann-Modells durch Morishima.

13.1.2 Die Verallgemeinerung des v.-Neumann-Modells durch Morishima

Morishima [1969] beseitigt die schwerwiegenden Einwände gegen das von Neumannsche Wachstumsmodell, indem er einen Endkonsum einfügt und die Arbeit aus der Menge der produzierten Güter herausnimmt, ohne das Modell zu zerstören. Er fasst die m Güter des von Neumann-Modells als produzierte Güter ohne Arbeit auf und fügt die Arbeit als 0-tes Gut hinzu. Dabei ist eine vorgegebene Wachstumsrate der Arbeit zugelassen. Das Modell sieht dann im einzelnen wie folgt aus.

Es sei a0 := (a01 ,...,a0n)’ der (konstante) Input-Vektor für Arbeit für die n Produktionsprozesse, cA := (cA1 ,...,cam)’ der Vektor der Ausgabenkoeffizienten für die Arbeiter, wobei cAm die Menge des Gutes m angibt, die die Arbeiter pro Einheit ihres verbrauchbaren Einkommens ausgebne. ....

... Das Gesamteinkommen teilt sich auf Arbeiter und Kapitaleigner proportional zu Vermögensverteilung zwischen Arbeitern und Kapitalisten auf, und diese ist im langfristigen Gleichgewicht proportional zu ihren Sparbeträgen. ..."

Es folgen weiter Ableitungen, die die ursprünglichen Axiome entsprechend der Erweiterung der Theorie interpretieren und hier ebenfalls weggelassen werden. Es wird nun noch die abschließende Bewertung des Modells zitiert werden:

"Die Bedeutung des von Neumann-Modells in der Erweiterung von Morishima liegt darin, dass eine beliebige Disaggregation möglich ist. Man benötigt daher keinen Index für irgendeine Art "Kapital" und keine Fiktion von Einprodukt-Betrieben. ....

....Der von Neumann-Pfad spielt als "Turnpike" in der Theorie des optimalen Wachstums einer disaggregierten Wirtschaft eine besondere Rolle; ..."

Die weiteren im Zitat angegebenen Autoren werden im Literaturverzeichnis aufgeführt.

Es gibt eine Reihe weiterer Literatur zu diesem Thema die größtenteils aus den 60-er und 70-er Jahren und aus dem englischen Sprachraum stammt und die ich wegen meiner unbefriedigenden Englischkenntnisse bisher noch nicht gründlich auswertet habe.

Die generelle Kritik der zitierten Autoren kann ich nicht teilen. Das betrifft insbesondere den Vorwurf, dass dieser Modellansatz nicht in der Lage sei, den technischen Fortschritt zu berücksichtigen. Dagegen vertrete ich die Position, dass der technische Fortschritt ebend keine endogene Erscheinung des Wirtschaftssystems ist, sondern seine Ursachen in der gesamten Gesellschaft hat. Er wird z.B. sehr stark durch die kulturelle Entwicklung der Gesellschaft beeinflusst, zu der ja auch das Bildungssystem und die Wissenschaften gehören. Wenn also die Auswirkungen des technischen Fortschritts auf die Wirtschaftsentwicklung untersucht werden sollen, müssen diese als exogene Parameter in das System eingeführt werden und dessen Auswirkungen untersucht werden. das ist gut möglich, wie ich bereits an einem Beispiel gezeigt habe.

Meine Kritik geht in eine andere Richtung. Es wird im Wesentlichen nur versucht zu berechnen, ob es das anzustrebende wirtschaftliche Gleichgewicht (Optimum) bei möglichst großem Wachstum gibt, mit der stillschweigenden selbstverständlichen Annahme, dass es sich in der kapitalistischen Marktwirtschaft auch einstellen muss, sofern nur seine mögliche Existenz nachgewiesen werden kann. Dieser Vorwurf trifft allerdings die gesamte Volkswirtschaftslehre, die zur Erklärung der krisenhaften Konjunktur- und Wachstumsschwankungen ziemlich ratlos mit empirischen Ansätzen rumlamentiert. Für die Anwender des von-Neumann-Modells ist es aber besonders beschämend, dass sie auf halbem Wege stehen geblieben sind. Gerade der Name von Neumann ist ja mit der Entwicklung der Rechentechnik verbunden ist, die inzwischen die notwendigen Voraussetzungen geschaffen hat, um das Problem einer dynamischen Simulation einer Marktwirtschaft nach einem disaggregierten linearen von-Neumann-Modell zu berechnen.

Meine Kritik an den Kritikern des von-Neumann-Modells besteht daran, das sie zu fest an der Ideologie der kapitalistischen Marktwirtschaft kleben. Ein Modell, das keine befriedige Funktionsfähigkeit des Kapitalismus nachweisen kann, taugt offenbar nichts, und wenn das nach einigen Versuchen nicht gelingt, dann wird es fallen gelassen. Darin sehe ich auch den Grund warum offenbar in der Anwendung dieses Ansatzes nicht wesentlich weitergearbeitet wurde.

Das belegt die hartnäckige Kritik an der vermeintlichen Nicht-Berücksichtigung des technischen Fortschritts. Die Erkenntnis, dass eine kapitalistische Marktwirtschaft wegen ihrer existentiellen Abhängigkeit von einer ausreichenden Profitrate ein ständiges Wirtschaftswachstum braucht, macht in einer Zeit der offensichtlichen Grenzen der natürlichen Ressourcen den technischen Fortschritt zum rettenden Strohhalm der kapitalistischen Marktwirtschaft und diesen damit zur heiligen Kuh. Das eigentliche Problem besteht darin, dass bereits die einfache Version des von-Neumann-Modells nachweist, dass in einer stabilen kapitalistischen Marktwirtschaft die Profitrate nicht höher sein darf als die physische Wachstumsrate der Volkswirtschaft, aber welcher Kapitalist wäre noch mit einer derart geringen Profitrate an einer Investition interessiert. In diesem Fall sollte man aber nicht die ungeliebte Theorie fallen lassen, sondern mit der Theorie nach einem besseren Wirtschaftssystem suchen.

Die Kritik muss ich allerdings in der Weise relativeren, dass ich z.Z. noch keinen vollständigen Überblick über die diesbezügliche Literatur habe und es vielleicht weitergehende Literaturquellen zu diesem Thema gibt, oder laufende Untersuchungen bisher nicht veröffentlicht wurden. Auch ich beschäftige mich ja seit einiger Zeit mit dem Problem und es ist davon so gut wie nichts in der Öffentlichkeit bekannt geworden. Allerdings bin ich der Meinung, dass die Lösung dieses Problem sowohl von der Notwendigkeit als auch nach den Möglichkeiten aktuell auf der Tagesordnung steht.

Die mit dem Erscheinungsjahr 1995 letzte mir zugängliche sekundäre Literaturquelle, die in üblicher kurzer Darstellung das von-Neumann-Modell innerhalb der Wachstumstheorie erwähnt, deutet nicht darauf hin, dass in letzter Zeit nennenswert neues zu dem Thema erschienen ist. Es handelt sich hierbei um Vahlens Kompendium der Wirtschaftstheorie [19]. Auch Morishima, der wie oben bereits erwähnt, das von-Neumann-Modell weiterentwickelte, hat in einer Veröffentlichung von 1992 [13] zum Thema der Gleichgewichtstheorie, keine Hinweise zu wesentlich neue Aussagen auf dem Gebiet.

Sollten dem geneigten Leser zu diesem Thema Literaturquellen mit wesentlich weiterführenden Untersuchungen bekannt werden, so würde ich mich über einen Hinweis freuen.

Gegenüber den mir in der Literatur bekannt geworden Quellen zum von-Neumann-Modell haben meine Untersuchungen in folgenden Punkten weitere Fortschritte gemacht:

zurück   weiter