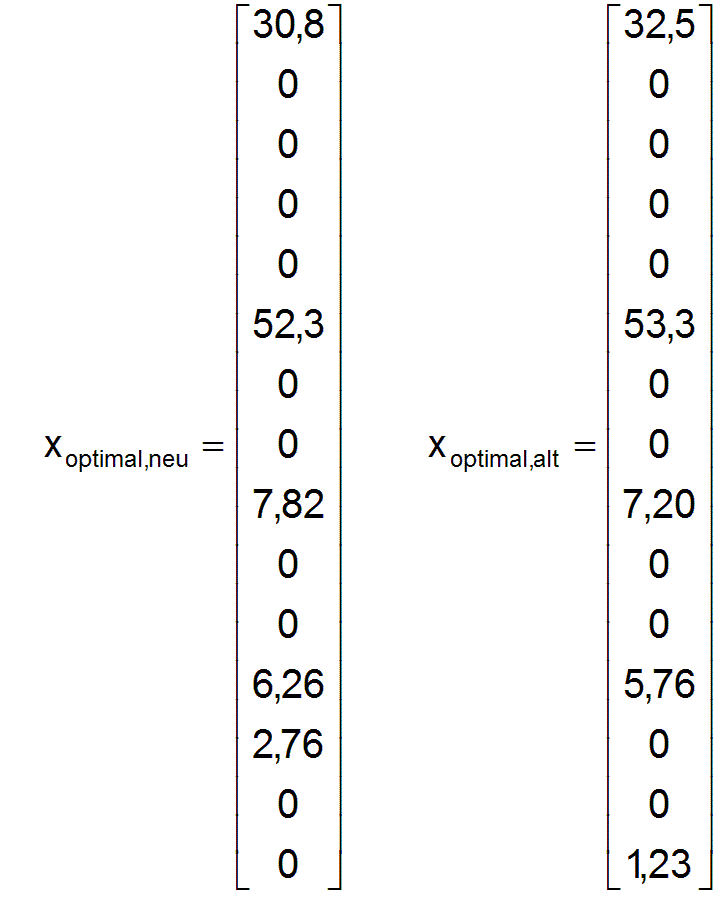
7 Einige ausgewählte Untersuchungen zur Demonstration der Leistungsfähigkeit der Modelle
Die Testrechnungen mit dem Demonstrationsbeispiel haben bereits einige interessante Ergebnisse gezeigt. Das soll nun an einigen weiteren ausgewählten Beispielen fortgesetzt werden.
zurück weiter7.1 Technischer Fortschritt
Technischer Fortschritt sind Verbesserungen der Produktionsverfahren, so dass mit gleichem Arbeitsaufwand mehr oder bessere Gebrauchsgegenstände produziert werden können, so dass entweder ein größerer zusätzlicher Konsum und/oder ein größeres Wirtschaftswachstum möglich wird. Technischer Fortschritt ist aber auch, wenn durch die Verbesserung der Produktionsverfahren weniger natürliche Ressourcen verbraucht oder benutzt werden. In diesem Sinne ist technischer Fortschritt prinzipiell als positiv und erstrebenswert anzusehen.
Ein leistungsorientiertes Wirtschaftssystem ist sicher eine begünstigende Bedingung für technischen Fortschritt. Es ist aber keine hinreichende Bedingung dafür. Weitere Voraussetzungen sind andere gesellschaftliche Voraussetzungen wie das Bildungssystem, das System wissenschaftlicher Einrichtungen, das Verhältnis von Grundlagen- und Anwendungsforschung und auch die ideologische Einstellung der Gesellschaft zu Innovationen (bundesdeutsch ausgedrückt das Wertesystem). Eine Besonderheit echter Innovationen ist dabei, dass ihre Entstehung zwar begünstigt, aber nicht erzwungen werden kann. In diesem Sinne ist technischer Fortschritt bezogenen auf die Volkswirtschaft eine von Außen wirkende (exogene) Erscheinung, die einerseits die Produktivität der Volkswirtschaft steigern kann, die anderseits aber auch eine Störung der Volkswirtschaft darstellt, weil mit der Einführung wesentlicher Innovationen meist auch Strukturveränderungen erforderlich werden.
Ein wesentlicher Kritikpunkt der Protagonisten der kapitalistischen Marktwirtschaft gegen das von-Neumann-Modell ist, dass der technische Fortschritt nicht dargestellt werden kann. Wenn dieser Vorwurf zutreffend wäre, müsste er auch für meine Modelle zutreffen. Das soll mit einem Demonstrationsbeispielen widerlegt werden.
Bezogen auf meine Wirtschaftsmodelle bedeutet technischer Fortschritt Veränderungen in den Parametern der Matrizen wi und wo. Diese Veränderungen können über bestimmte Zeiträume kontinuierlich sein ober sprunghaft durch Einführung qualitativ neuer Verfahren. Als exogene Erscheinung müssen sie für die Simulationsrechnung als Eingabeparameter vorgegeben werden und es kann dann die Reaktion des Systems auf diese Störung simuliert werden.
Ich verwende wieder mein Demonstrationsbeispiel, indem in einem Produktionsverfahren eine sprunghafte Produktivitätssteigerung stattfinden soll. Ich nehme an, dass zu Beginn ein optimale Wirtschaftsstruktur besteht, bezogen auf den bisherigen Entwicklungsstand der Produktivkräfte.
Im meinem Demonstrationsbeispiel wird die Ware i3=5 (Energie) durch die Produktionsverfahren i2= 13, 14 und 15 produziert. Bisher war das Verfahren i2=15 das produktivste, so dass in der aktuellen optimalen Wirtschaftsstruktur z.Z. ausschließlich mit diesem Verfahren produziert wird. Es findet nun eine Innovation statt, die das Verfahren i2=13 sprunghaft verbessert, indem bei gleichem Input wi13 der Output des Produkts wo13,5 von bisher 5 auf 10 erhöht wird.
Mit Hilfe des Berechnungsverfahrens gemäß Abschnitt 5 kann zunächst die Veränderung der neuen optimalen Wirtschaftsstruktur xoptimal,neu berechnet und mit der alten verglichen werden.
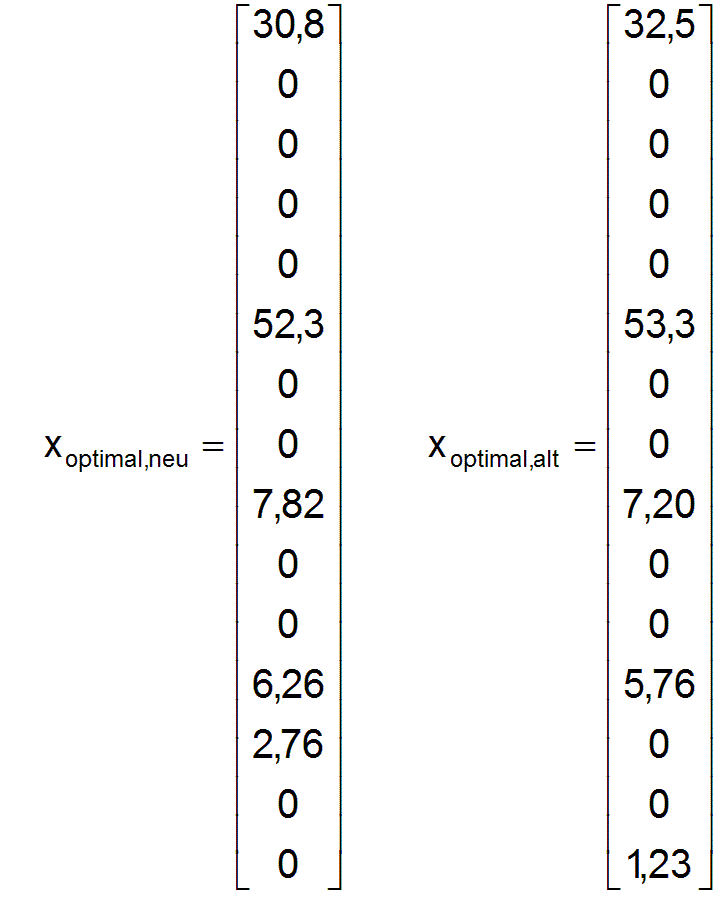
Da jetzt das Verfahren i2=13 offenbar produktiver ist als das Verfahren i2=15, hat es einen Wechsel gegeben in der Beteiligung an der optimalen Wirtschaftsstruktur in der Branche der Energieerzeuger. Damit verändert sich natürlich auch das erforderliche optimale Warensortiment wgoptimal und das optimale Preissystem preiswoptimal
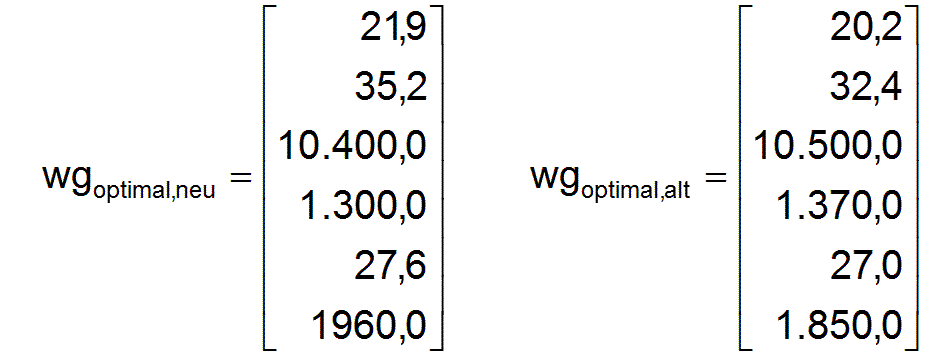

Der Preis der Ware i3=5 hat sich erwartungsgemäß erheblich verändert. Das hat sich auch auf die anderen Preise ausgewirkt, durch die damit veränderte Kostenstruktur der anderen Unternehmen.
Durch den technischen Fortschritt in einem Produktionsverfahren verbessert sich auch die gesamtgesellschaftliche Produktivität, was ausgedrückt wird durch die Möglichkeit eines erhöhten zusätzlichen Konsums
flmax,neu = 0,794 flmax,alt = 0,677
Durch die Optimierungsrechnung ist angegeben, welche Strukturwandlungen erforderlich sind, von der alten optimalen Wirtschaftsstruktur zur neuen optimalen Wirtschaftsstruktur. Interessant ist nun zu beobachten wie die verschiedenen Wirtschaftsmodelle diesen Strukturwandel verkraften. Das eigentliche Problem ist hierbei, dass bisher kein Unternehmen existiert, welches nach dem jetzt produktiveren Verfahren arbeitet und deshalb neu gegründet werden muss. Außerdem muss das unproduktivere Unternehmen stillgelegt werden, wobei die verbleibenden Produktionsmittel durch andere Unternehmen weiter genutzt werden sollten.
Mit meinem ersten Modell einer kapitalistischen Marktwirtschaft ohne Kapitaltransfer lohnt ein Versuch der Anwendung aus zwei Gründen nicht. Erstens ist ohne Kapitaltransfer eine Neugründung eines Unternehmens nicht möglich. Dieser Mangel wäre im Modell behebbar, indem ein Kapitalmarkt eingeführt wird, was ich übrigens probehalber auch mal praktiziert habe. Der zweite und entscheidende Grund ist aber: Da das System nicht einmal im Optimum stabil ist, ist eine Selbstoptimierung beim Strukturwandel erst recht nicht zu erwarten. Deshalb wird auch in allen folgenden Untersuchungen dieses Modell nicht mehr in Betracht gezogen.
Nun wird das Verhalten des Modells einer Planwirtschaft untersucht. Es wurden 50 Reproduktionszyklen berechnet. In den ersten 10 Zyklen herrschen noch optimale Verhältnisse nach dem bisherigen Entwicklungsstand der Produktivkräfte. Vom 10. zum 11. Zyklus hat sich das Produktionsverfahren i2=13 sprunghaft verbessert. Es beginnt ein Selbstoptimierungsprozess. Beim 50. Zyklus hat sich die neue optimale Wirtschaftsstruktur bereits wieder eingestellt.
Bild 24 zeigt die Entwicklung der Warenpreise preisw. Die Umstellung ist nach weniger als 10 Zyklen erfolgt. Der Preis der Ware i3=5 fällt erheblich, weil es jetzt weniger Aufwand macht diese Ware herzustellen. Alle anderen Warenpreise sinken auch etwas, weil durch den Preisverfall der einen Ware die Fertigungskosten der anderen Waren durch den niedrigeren Kostenanteil des Produktionsinput ebenfalls sinken.
Bild 25 zeigt die Entwicklung der Wachstumsfaktoren fwi3 in den einzelnen Warenarten. Diese zeigen wie das Optimum der Wirtschaftsstruktur durch Einführung der Innovation zunächst gestört wird und wie diese Störung wieder abklingt. In diesem Modell sind die sichtbaren Störungen nach ca. 20 Zyklen abgeklungen.
Bild 26 zeigt die Entwicklung der Bevölkerungszahlen a, die Anzahl ak der versorgten Arbeiter und die Anzahl aeg der beschäftigten Arbeiter. Der plötzliche eingeleitete Strukturwandel bewirkt zunächst eine Unterversorgung der Bevölkerung und damit ein Sinken der Bevölkerungszahl. Nach ca. 7 Zyklen ist wieder Vollversorgung (rak=1) gegeben. Wegen des vorgegebenen Wachstumsfaktors fa=1 in diesem Beispiel kann der Bevölkerungsverlust nicht wieder ausgeglichen werden und die optimale Wirtschaftsstruktur muss sich auf einem niedrigeren Niveau einpegeln. Durch den geringeren Bedarf an Warenbeständen wg, der im Wesentlichen aus dem Bevölkerungsschwund resultiert, kommt es zu Teilbeschäftigung aeg<a, die nach ca. 25 Zyklen wieder vorbei ist. In diesem Modell ist Unterbeschäftigung aber keine Ursache für Unterversorgung, weil die Arbeiter die Konsumgüter nicht für erarbeiteten Lohn kaufen, sondern in Abhängigkeit der verfügbaren Waren zugewiesen bekommen.
Bild 27 zeigt die Entwicklung des Faktors fl des zusätzlichen Konsums (neben den Faktoren rak und raeg). Der zusätzliche Konsum steigt innerhalb von ca. 10 Zyklen auf das neue Niveau an. Bemerkenswert ist hier, dass einerseits die Bevölkerungszahl wegen Unterversorgung mit den notwendigen Konsumgütern sinkt und anderseits sofort der Faktor des zusätzlichen Konsums steigt. Würde man ein derartiges Anpassungsverhalten der Wirtschaft in einem realen Wirtschaftssystem beobachten, wäre das dringend verbesserungsbedürftig.
Nun wird das Verhalten des Modells einer anderen Marktwirtschaft untersucht. Es hat sich ja bereits gezeigt, dass dieses Modell nicht prinzipiell zum Optimum konvergiert, sondern diese Konvergenz nur durch Verwendung geeigneter Faktoren f3, f4 und f5 erreicht werden kann. Die Störung des wirtschaftlichen Gleichgewichts durch dieses Beispiel einer Innovation war bereits so groß, dass zunächst keine geeigneten Faktoren f3, f4, f5 gefunden werden konnten, die ein dauerhaftes Optimum bewirkten. Erst durch Änderung einer Formel innerhalb des Modell konnte die Konvergenz erreicht werden. Es ist die Formel (62), die am Ende jedes Reproduktionszyklus den Faktor fl des zusätzlichen Konsums anpasst. Diese wurde ersetzt durch
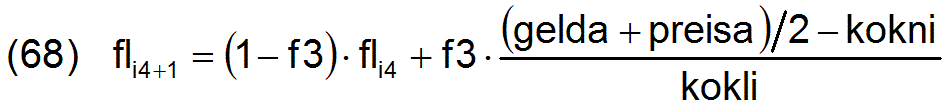
Es wurde hier also neben dem verfügbaren Geld gelda pro Arbeiter noch zusätzlich der Preis preisa der Arbeitskraft eingefügt. Damit und mit den Faktoren f3=0,05 f4=5 und f5=0,05 wurde Konvergenz erreicht.
Diese Formel wird deshalb aber nicht generell in das Modell eingebaut, weil sie bei anderen Beispielen auch zu Problemen führt. Es besteht noch ein erheblicher Forschungsbedarf. Hier soll aber nicht tiefer in die Problematik eingedrungen werden, da das Modell zunächst nur ein Studienmodell ist und an einem wesentlich zu modifizierenden Modell, welches dann auch als realistische Version für die Gesellschaft dienen sollte, diese Untersuchungen noch gründlicher fortzuführen sind.
Zurück zu unserem Beispiel. Insgesamt erfolgt die Konvergenz zur neuen optimalen Wirtschaftsstruktur wesentlich langsamer als beim Modell der Planwirtschaft. Es wurden deshalb 200 Reproduktionszyklen berechnet. In den ersten 10 Zyklen herrschten wieder die optimalen Bedingungen gemäß dem bisherigen Entwicklungsstand der Produktivkräfte.
Bild 28 zeigt wieder die Entwicklung der Warenpreise. Die Konvergenz ist sehr gut. Das Optimum ist nach ca. 40 Zyklen erreicht.
Bild 29 zeigt die Entwicklung der Wachstumsfaktoren fwi3 in den einzelnen Warenarten. Hier ist zuerkennen, dass die Störung infolge der Einführung der Innovation über die nächsten 200 Zyklen nur langsam abklingt. Dementsprechend ist auch der Abfall der Bevölkerungszahl Bild 29a infolge von Unterversorgung größer als im Modell der Planwirtschaft (Vergleiche mit Bild 26). Die Vollversorgung und damit das Ende des Bevölkerungsrückgangs ist nach ca. 80 Zyklen wieder hergestellt.
Bild 30 zeigt die Entwicklung des Faktors fl des zusätzlichen Konsums (neben den Faktoren rak und raeg). Auch in diesem Modell steigt der Faktor fl sofort stark an, obwohl unter anderem dadurch zunächst nicht die volle Versorgung der Arbeiter mit den notwendigen Konsumgütern gegeben ist. Der Faktor fl schwingt sogar noch über und strebt erst danach den neuen Optimalwert an. Es kann also auch bei diesem Modell einer Marktwirtschaft für dieses Beispiel noch nicht von einer sozialen Marktwirtschaft die Rede sein.
Einen interessanten Einblick in den simulierten Strukturwandel gibt Bild 31.1. Hier wurden übereinander geschichtet die Wertanteile der investierten Güter der einzelnen Unternehmen und der konsumierenden Arbeiter angegeben. Der Wert Eins entspricht dem Gesamtwert aller verfügbaren Waren zu aktuellen Preisen. Damit zeigt die oberste Kurve den anteiligen Gesamtwert der z.Z. für die Reproduktion genutzten Waren. Die Differenz zwischen Eins und der obersten Kurve zeigt den wertmäßigen Anteil der z.Z. nicht genutzten Waren. Der Zwischenraum zwischen der obersten Kurve und der nächsten darunterliegenden zeigt den wertmäßigen Wareninput des Unternehmens i2=15, welches bis zum 10.Zyklus noch das produktivsten Unternehmen seiner Branche ist und deshalb an der bisherigen optimalen Wirtschaftsstruktur beteiligt ist. Der nächste Zwischenraum zwischen der 2. und der 3. Kurve zeigt den wertmäßigen Wareninput des Unternehmens i2=13, welches nach Einführung der Innovation das produktivste Unternehmen der Branche ist und das Unternehmen i2=15 vom Markt verdrängt. Diese Verdrängung ist in diesem Diagramm von Zyklus i4=10 bis 40 gut zu erkennen. Bild 31.2 zeigt den gleichen Sachverhalt mit einem anderen Maßstab der Zeitachse über alle 200 berechneten Reproduktionszyklen. Hier ist zu erkennen, wie nach Vollendung der Verdrängung infolge der Störung des Wirtschaftssystem ein langsames Abklingen von Schwingungen in der Struktur erfolgt, die auch in Bild 29 zu sehen waren, die sich in ihrer Endphase aber nicht mehr negativ auf die Versorgung und die Beschäftigung der Arbeiter auswirken.
Schlussfolgerung: Das Modell der Planwirtschaft und das Modell einer anderen Marktwirtschaft sind geeignet, Erscheinungen des technischen Fortschritts plausibel zu simulieren. Sie können als vorläufige Studienmodelle wertvolle Erfahrungen liefern, die in ein weiterzuentwickelndes realistisches Modell einer sozialen Markt- und/oder Planwirtschaft eingehen können.
zurück weiter