Anhand unseres Demonstrationsbeispiels soll nun die Funktion des Modells getestet werden.

Als erstes soll geprüft werden, ob das Modell in der Lage ist, eine optimale Wirtschaftsstruktur aufrecht zu erhalten. Dazu werden wieder die mit dem Simplexalgorithmus berechneten optimalen Anfangsparameter ergänzt durch das zugehörige optimale Preissystem auf jeweils drei Ziffern gerundet.

In dem Modell sind drei Faktoren f3, f4, f5 eingebaut, die das Selbstregelverhalten des Systems beeinflussen. Der Faktor f3 bestimmt die Geschwindigkeit, mit der der Faktor fl des zusätzlichen Konsums verändert wird. Der Faktor f4 bestimmt, wie viel mal der Warenüberschuss gegenüber der Nachfrage je Warenart und Reproduktionszyklus größer sein darf, bevor der Markt seine Nachfrage einstellt. Der Faktor f5 bestimmt die Geschwindigkeit, mit der der Kapitaltransfer zwischen den Unternehmen erfolgt.

Um das Ergebnis vorweg zu nehmen, das System ist nicht prinzipiell stabil, die Stabilität des Systems kann wesentlich durch diese drei Faktoren beeinflusst werden.

Im ersten Beispiel werden die drei Faktoren mit folgenden empirisch ermittelten Werten belegt:

Das führt zu einem stabilen System. In den folgenden Diagrammen wurde die Ordinate sehr stark gestreckt, um die geringen Veränderungen, die sich alle dicht um das Optimum abspielen, zu zeigen.

Bild 12 zeigt die Preisentwicklung der Ware i3=1 stellvertretend für alle anderen Waren über 20 Reproduktionszyklen. Nach ca. 10 Zyklen ist die durch Rundung entstandene sichtbare Abweichung vom Optimum bereits abgeklungen.

Bild 13 zeigt die Faktoren der Warenreproduktion fw_i3, die bei fa=1 gegen eins streben sollen. Nach ca. 80 Reproduktionszyklen sind auch hier die sichtbaren Abweichungen vom Optimum abgeklungen. Schwankungen bei diesen Faktoren deuten auf Disproportionen in den realisierten Warenproduktionen hin. Diese zeigen offenbar eine geringere Neigung zur Konvergenz zum Optimum.

Bild 14 zeigt die Bevölkerungsentwicklung. Bereits durch geringe Abweichungen kommt es zu Störungen, die sich in diesem Modell auch auf die Versorgung auswirken, so dass ein geringer Bevölkerungsrückgang auftritt, der wegen fa=1 nicht ausgeglichen werden kann.

Bild 15 zeigt die Entwicklung des Faktors fl des zusätzlichen Konsums. Obwohl der Faktor am Anfang bereits den optimalen Wert hat, wird dieser durch die Abweichungen der anderen Parameter vom Optimum zunächst gestört und kehrt dann allmählich zu seinem optimalen Wert zurück.

Im zweiten Beispiel werden die drei Faktoren mit folgenden Werten belegt:

Das führt zu einem instabilen System. Es ist zu beachten, dass wegen der größer werdenden Abweichungen für die Ordinatenachsen der folgenden Diagramme wesentlich andere Maßstäbe verwendet wurden.

Bild 16 zeigt wieder die Preisentwicklung der Ware i3=1 stellvertretend für alle anderen Waren. Nach ca. 10 Zyklen ist die durch Rundung entstandene Abweichung vom Optimum bereits abgeklungen. Bezüglich der Preise ist das System weiterhin stabil. Es wird von der Veränderung des Faktors f3 kaum beeinflusst. (Vergleiche mit Bild 12)

Bild 17 zeigt die Wachstumsfaktoren fw_i3, die bei fa=1 gegen eins streben sollten. Das Gegenteil ist der Fall. Es ist deutlich zu erkennen, wie sich das System aufschaukelt.

Bild 18 zeigt die Anzahl a der Arbeiter, die Anzahl ak der versorgten Arbeiter und die Anzahl aeg der beschäftigten Arbeiter . Auch hier ist das Aufschaukeln des instabilen Systems deutlich zu erkennen, mit dem Effekt, dass durch Unterversorgung und Unterbeschäftigung die Bevölkerung zugrunde geht.

Als drittes Beispiel soll nun unser Demonstrationsbeispiel mit nicht optimalen Anfangsbedingungen, durchgerechnet werden, wie es schon für das Modell der Planwirtschaft gezeigt wurde.

Es gibt zu Beginn wieder a=100 arbeitsfähige Mitglieder (Arbeiter) der Gesellschaft.

Mit fa=1 ist der Faktor der Vermehrung der versorgten Arbeiter angegeben.

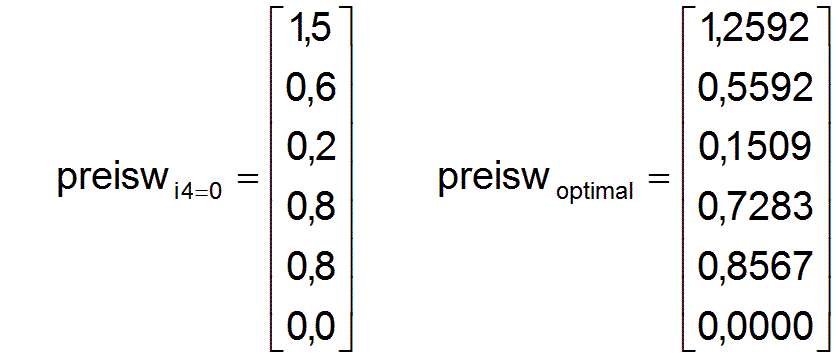
Es ist ein nicht optimales Preissystem preisw_i4=0 gegeben. Zum Vergleich ist das optimale Preissystem preisw_optimal mit angegeben.

Der Preis der Arbeitskraft preisa bleibt als Basispreis bekanntlich konstant und ist mit preisa=1 angegeben.

Weiterhin ist ein nicht optimales Sortiment an Warenmengen wg_i4=0 gegeben. Zum Vergleich ist wieder das optimale Sortiment an Warenmengen wg_optimal mit angegeben.

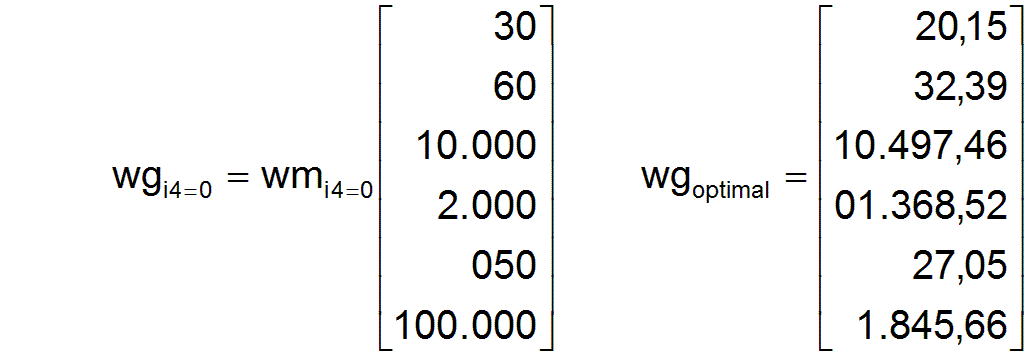
Für den ersten Reproduktionszyklus wird der Faktor fl_i4=1 = 0,6 angenommen. Der optimale wäre fl_optimal =0,6768.

Für dieses Beispiel sind im Unterschied zu dem planwirtschaftlichen Modell auch die Parameter geldaa, geldu, geldo, wk, wm und wu anzugeben, die die Besitzverhältnisse beschreiben. Es werden der einfachheitshalber am Anfang die gesamten Warenmengen dem zentralen Markt zugeordnet . Alle anderen Warenmengen sind leer wk=Æ und wu=Æ . Den Arbeitern und den Unternehmen werden aber entsprechende Geldmengen geldaa und geldu zugeordnet, so dass sie ihre komplette Erstausstattung an Konsumgütern und Produktionsmitteln kaufen können, sofern der Vorrat reicht. Das Konto geldo der Kapitaleigentümer zur Zwischenbuchung bei Kapitaltransfer ist zu Beginn leer . Zum Vergleich werden auch hier zusätzlich die optimalen Parameter angegeben.

   geldaa_i4=0 = 600     geldaa_optimal = 667     geldo_i4=0 = 0

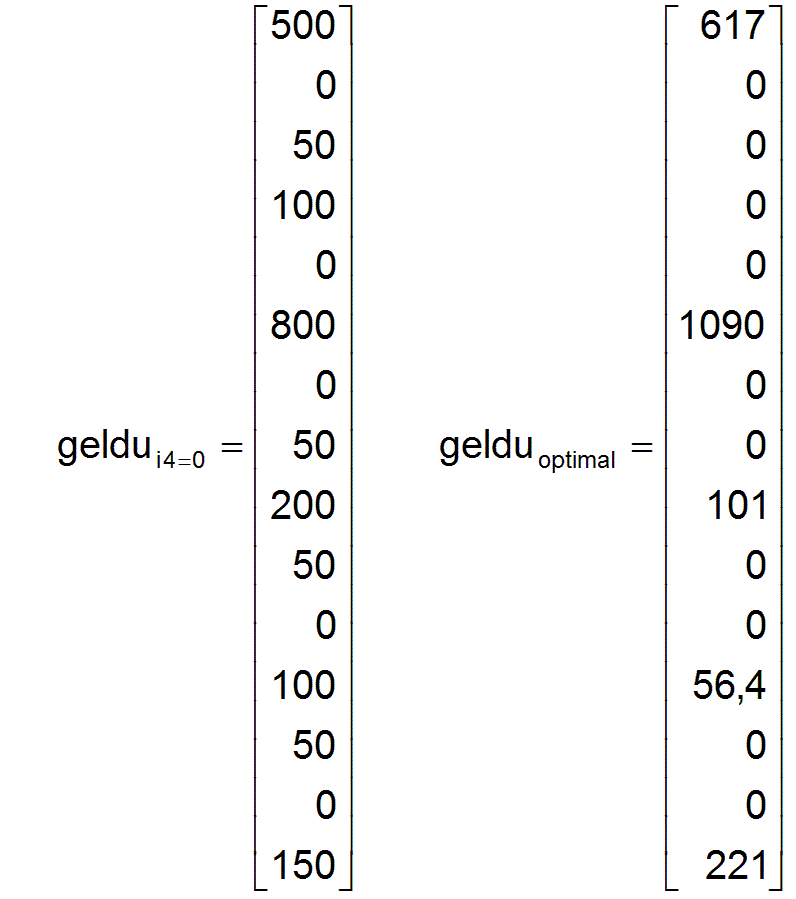
Alle anderen konstanten Parameter kni, kno, kli, klo, ai, wi und wo wurden oben bereits angegeben und wurden in dieser Größe beibehalten.

Auch für die Faktoren f3, f4 und f5 sind Werte festzulegen. Durch probieren wurden Werte gefunden, die eine recht gute Konvergenz bewirkt haben.

Das bestätigt auch hier, dass Selbstoptimierung nicht prinzipiell gegeben ist.

In diesem Beispiel treten zwar teilweise recht große Abweichungen vom Optimum auf. Es wurden auch einige Unternehmen mit Kapital versehen, die nicht an einer optimalen Wirtschaftsstruktur beteiligt sind. Die Kapitalverteilung, wie auch die anderen nicht optimalen Anfangsparameter wurden jedoch nicht völlig dem Zufall überlassen. Die angestrebte optimale Struktur ist bereits in groben Zügen zu erkennen.

Mit diesen Abweichungen ist das Modell in der Lage selbstregelnd das Optimum zu erreichen. Es ist bisher aber nicht gelungen von beliebigen Anfangssituationen eine Selbstregelung zum Optimum zu simulieren. Dazu sind weitere Untersuchungen erforderlich.

Bild 19 zeigt die Preisentwicklung. (Vergleiche auch mit Bild 6.)

Bild 20 zeigt die Faktoren der Warenakkumulation fw_i3, die bei fa=1 gegen eins streben müssen. Hier ist nach anfänglichen starken Schwankungen innerhalb von 50 Reproduktionszyklen das Optimum ebenfalls erreicht. (Vergleiche auch mit Bild 8.)

Bild 21 zeigt die Entwicklung der Bevölkerungszahl a, die Anzahl ak der versorgten Arbeiter und die Anzahl aeg der beschäftigten Arbeiter. Im ersten Reproduktionszyklus ist ein starker Rückgang der Bevölkerungszahl zu sehen, da offenbar beim Konsumgut i3=3 (Wohnraum) anfänglich ein Engpass besteht. Danach ist Vollversorgung und Vollbeschäftigung fast durchgängig gegeben, obwohl die Wirtschaftsstruktur noch ca. 50 Reproduktionszyklen bis zum Optimum benötigt. Da mit fa=1 keine Möglichkeit des Wiederanwachsens der Bevölkerung gegeben ist, muss sich die optimale Wirtschaftsstruktur jetzt auf einem niedrigeren Niveau einpegeln.

Bild 22.1 und Bild 22.2 zeigen die Verteilung der beschäftigten Arbeiter auf die verschiedenen Unternehmen über verschiedene Zeitintervalle. Im Bild 22.1 ist zu erkennen, wie die nicht so produktiven Unternehmen innerhalb der ersten 10 Reproduktionszyklen aus der Wirtschaft verdrängt werden. Im Bild 22.2 ist dann zu erkennen, wie sich zwischen den verbleibenden produktivsten Unternehmen optimale Proportionen im Produktionsvolumen einstellen.

Bild 23 zeigt wie der Faktor des zusätzlichen Konsums, der zunächst einen Einbruch erlebte, sich allmählich dem Optimum nähert.

Bisher habe ich noch nicht untersucht, welche verallgemeinerungsfähigen Kriterien an die Auswahl der Regelparameter f3,f4 und f5 zustellen sind, um ein stabiles System zu erhalten. Bisher habe ich durch probieren entsprechende Parameter gefunden.

Als positives Resultat können wir zunächst für dieses Modell einer Marktwirtschaft registrieren, dass hiermit ein Modell gefunden wurde, welches unter bestimmten Bedingungen in der Lage ist, sich selbst zu optimieren.