Erste Testrechnungen mit optimalen Anfangsparametern haben gezeigt, das dieses Modell in seinem Optimum stabil ist.

Nachfolgende Testrechnungen mit nicht optimalen Anfangsbedingungen haben weiter gezeigt, dass dieses Modell sehr gute selbstoptimierende Eigenschaften besitzt.

Das soll zunächst an unserem bereits mehrfach benutzten Demonstrationsbeispiel gezeigt werden.

Es gibt zu Beginn a=100 arbeitsfähige Mitglieder (Arbeiter) der Gesellschaft.

Mit fa=1 ist der Faktor der Vermehrung der versorgten Arbeiter angegeben.

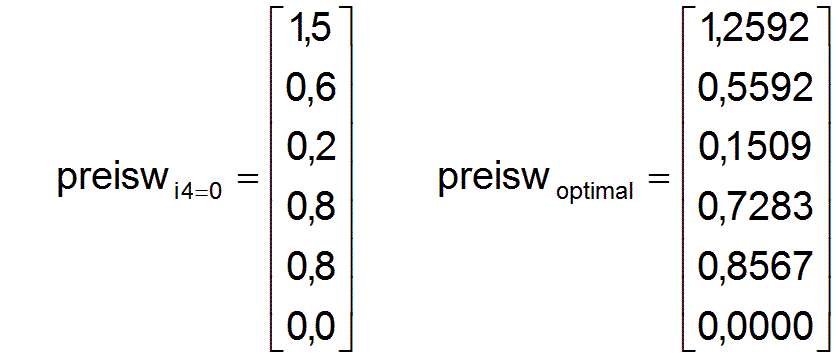
Es ist ein nicht optimales Preissystem preisw_i4=0 gegeben. Zum Vergleich ist das optimale Preissystem preisw_optimal hier mit angegeben.

Der Preis der Arbeitskraft preisa bleibt als Basispreis bekanntlich konstant und ist mit preisa=1 angegeben.

Weiterhin ist ein nicht optimales Sortiment an Warenmengen wg_i4=0 gegeben. Zum Vergleich ist wieder das optimale Sortiment an Warenmengen wg_optimal mit angegeben.

Für den ersten Reproduktionszyklus wird der Faktor fl_i4=1 = 0,6 angenommen. Der optimale wäre fl_optimal =0,6768.

Alle anderen konstanten Parameter kni, kno, kli, klo, ai, wi und wo wurden oben bereits angegeben und wurden in dieser Größe beibehalten.

Parameter für die Beschreibung der Eigentumsverhältnisse wie z.B. geldaa, wk, geldu, wu und wm brauchen nicht angegeben werden, da wegen der zentralen Güterzuweisungen in jedem Zyklus Eigentumsverhältnisse keine Rolle spielen. Im Prinzip sind alle Gütermengen wg gesamtgesellschaftliches Eigentum.

Bild 6 zeigt die Preisentwicklung. Bereits nach ca. 10 Reproduktionszyklen haben sich die optimalen Preise eingestellt. Das ist eine ausgezeichnete Konvergenz.

Bild 7 zeigt die Entwicklung der Unternehmensgewinne dargestellt durch die Gewinnfaktoren fgewinnu0_i2 (Definition siehe Gleichung (19)). Da bei fa=1 kein Bevölkerungswachstum stattfindet und technischer Fortschritt auch nicht angenommen wird, findet auch kein Wirtschaftswachstum statt. Deshalb müssen die Gewinnfaktoren der Unternehmen, die an der optimalen Wirtschaftsstruktur beteiligt sind, gegen Eins streben. Es ist gut zu erkennen, wie die Gewinnfaktoren von 5 Unternehmen bereits nach ca. 10 Reproduktionszyklen gegen Eins streben. Das ist eine direkte Folge der schnellen Konvergenz der Preise zu den Optimalwerten. Die Gewinnfaktoren aller anderen Unternehmen ordnen sich darunter an, d.h. sie sind nicht konkurrenzfähig.

Bild 8 zeigt die Faktoren der Warenakkumulation fw_i3 ,die bei fa=1 gegen Eins streben müssen. Hier ist nach anfänglichen starken Schwankungen innerhalb von 20 Reproduktionszyklen das Optimum ebenfalls erreicht.

Bild 9 zeigt die Entwicklung der Bevölkerungszahl a, die Anzahl ak der versorgten Arbeiter und die Anzahl aeg der beschäftigten Arbeiter. Auch hier hat sich nach ca. 20 Reproduktionszyklen das Optimum eingestellt. Durch die anfänglichen wirtschaftlichen Disproportionen ist durch zeitweilige Unterversorgung der Bevölkerung die Bevölkerungszahl gesunken. Das ist in diesem Beispiel auf den anfänglichen Engpass der Güterart i3=3, die Gebäude, zurückzuführen. Da mit fa=1 keine Möglichkeit des Wiederanwachsens der Bevölkerung gegeben ist, muss sich die optimale Wirtschaftsstruktur jetzt auf einem niedrigeren Niveau einpegeln. Die anfängliche Unterbeschäftigung ist darauf zurückzuführen, dass durch geringere Produktion der Güter, bei denen Überbestände existieren, diese erst abgebaut werden. Da hier die Bevölkerung durch Warenzuweisung versorgt wird, entsteht durch die Unterbeschäftigung keine Unterversorgung der Arbeiter.

Das gleiche Demonstrationsbeispiel wurde noch einmal mit einer Variation durchgerechnet. Statt fa=1 wurde fa=1,004 gesetzt, so dass ein Bevölkerungswachstum und ein Wirtschaftswachstum möglich wird. Die Konvergenz zum Optimum ist genauso gut.

Bild 10 zeigt wieder die Gewinnfaktoren fgewinnu0_i2. Es ist zu erkennen, dass sich jetzt die Gewinnfaktoren der 5 Unternehmen, die an der optimalen Wirtschaftsstruktur beteiligt sind, auf einen einheitlichen Gewinnfaktor über Eins, nämlich bei 1,004, einpegeln. Die Gewinnfaktoren der nicht konkurrenzfähigen Unternehmen liegen wieder darunter.

Bild 11.1 zeigt wieder die Entwicklung der Bevölkerungszahl a, die Anzahl ak der versorgten Arbeiter und die Anzahl aeg der beschäftigten Arbeiter über die ersten 50 Reproduktionszyklen. Auch hier gibt es den anfänglichen Einbruch in der Bevölkerungszahl, die nach ca. 6 Reproduktionszyklen wieder zu wachsen beginnt. Bild 11.2 zeigt den selben Sachverhalt diesmal über 200 Reproduktionszyklen. Es ist zuerkennen, wie nach ca.20 Zyklen das ursprüngliche Niveau von 100 Arbeitern wieder erreicht ist und danach die Bevölkerung und demnach auch die Wirtschaft mit dem Faktor 1,004 pro Reproduktionszyklus kontinuierlich weiter wächst. Falls keine weitere Störung eintritt, wird in diesem Beispiel die Bevölkerung und die Wirtschaft weiter wachsen, bis die Ware i3=6 (Grund und Boden), die nicht produziert werden kann, sondern ohne zu verschleißen nur benutzt wird, vollständig in Gebrauch ist. Aber dazu später.

In diesem Beispiel weichen die Anfangsparameter noch recht wenig vom Optimum ab. Bei allen bisherigen auch wesentlich extremeren Testbeispiele wurde mit Hilfe dieses Wirtschaftsmodells letztendlich das Optimum gefunden. Allerdings traten dabei zwischenzeitlich auch verheerende Ereignisse für die Bevölkerung ein, was sich immer am zeitweiligen Rückgang der Bevölkerungszahlen erkennen lässt, der durch Unterversorgung verursacht wird.

Das soll an Beispielen zunächst reichen. Es soll an dieser Stelle auch nicht weiter diskutiert werden, welche Realisierungsmöglichkeiten diese Planwirtschaft oder Planwirtschaften überhaupt haben. Als positives Ergebnis dieses Modells soll zunächst nur festgehalten werden, dass es mir hiermit erstmals gelungen ist, ein theoretisches Wirtschaftsmodell zu konstruieren, das in der Lage ist, sich selbst zu optimieren. Bei dieser Komplexität der Parameter, die sich alle verändern können und jede Veränderung eines Parameters sofort Änderungen anderer Parameter nach sich zieht, erschien es mir nicht selbstverständlich, dass es überhaupt gelingt.

Als weiteres positives Ergebnis ist die ausgezeichnete Konvergenz der Preise zum Optimum durch das Prinzip der Preisbildung durch Kalkulation der Kosten anzusehen.