Die Optimierungsrechnungen des Simplexalgorithmus liefern noch nicht die optimale Preisstruktur, wie sie in der Testrechnung mit dem Modell der kapitalistischen Marktwirtschaft bereits angegeben wurden. Das liegt daran, das für eine optimale materiell-technische Wirtschaftsstruktur noch nicht von Bedeutung ist, durch welche Produktionsverhältnisse sie zustande gekommen ist und ob demzufolge bei ihrer Realisierung Geld überhaupt eine Rolle gespielt hat. Deshalb sind weitere Überlegungen für die Berechnungen eines optimalen Preissystems innerhalb einer Marktwirtschaft erforderlich.

Annahmen:

1. Bei einem optimalen Preissystem in einer optimalen Wirtschaftsstruktur, die nicht durch äußere Einflüsse gestört wird, sollen sich die Preise über die Zeit nicht ändern.
2. Jedes Unternehmen muss aus den Einnahmen des Verkaufs seiner Produkte im letzten Reproduktionszyklus, den Ersatz der verschlissenen bzw. verbrauchten Produktionsmittel, den Kauf von Arbeitskräften und die zusätzlichen Investitionen infolge eines möglichen Wirtschaftswachstums aufgrund des Bevölkerungswachstums für den nächsten Reproduktionszyklus finanzieren.
3. Die Arbeiter müssen aus ihren Löhnen des letzten Reproduktionszyklus den Ersatz ihrer verschlissenen bzw. verbrauchten Konsumgüter und die zusätzlich notwendigen Konsumgüter infolge eines möglichen Bevölkerungswachstums finanzieren.

Aus der vorangegangenen Optimierungsrechnung nach dem Simplex-Algorithmus ist bekannt, welche ausgewählten Unternehmen ii2 in der optimalen Wirtschaftsstruktur an der Produktion beteiligt sind. Für den Fall, dass n3 Waren produziert werden, dass kein Abfall anfällt und dass unter diesen Bedingungen ein maximaler zusätzlicher Konsum realisiert wird, sind das genau n3 Unternehmen ii2.

Für den allgemeinen Fall, dass n3 Waren i3 produziert werden, dass aber davon n5 Waren ii3 regelmäßig zum Teil als Abfall deponiert werden müssen, und dass unter diesen Bedingungen wiederum ein maximaler zusätzlicher Konsum realisiert wird, sind es nur noch (n3-n5) Unternehmen ii2, die an einer optimalen Wirtschaftsstruktur beteiligt sind.

Weiterhin sind gegeben der Bevölkerungswachstumsfaktor fa, die Versorgungsrate rak und die Beschäftigungsrate raeg.

Die Beschäftigungsrate liegt im Intervall 0<raeg£ 1.

Für die Versorgungsrate rak wird zwar regelmäßig der Wert 1 angestrebt. Im allgemeinen Fall sind für rak aber auch alle Werte im Intervall 0<rak£ 1 möglich.

Für den allgemeinen Fall rak<1 weicht das tatsächliche Bevölkerungswachstum mit dem Faktor fae von dem Bevölkerungswachstum bei Vollversorgung (Faktor fa) ab. Das Wirtschaftswachstum muss dem tatsächlichen Bevölkerungswachstum entsprechen.

Der Faktor fae für das tatsächliche Bevölkerungswachstum und damit auch für das Wirtschaftswachstum ist gemäß Gleichung (7) fae=fa* rak .

Gesucht ist ein optimales Preissystem bestehend aus preisa und preisw_i3 für i3=1 bis n3.

Es ist klar, dass zu jedem ermittelten Preissystem jedes Vielfache der Preise ein gleichwertiges Preissystem darstellt. Deshalb muss für eine Warenart der Preis willkürlich festgesetzt werden. Das ist der Basispreis zu dem sich dann alle anderen Preise in entsprechender Relation errechnen. Aufgrund der historischen Entwicklung des Geldes war das früher der Goldpreis. Ich halte es für sinnvoller den Wert der Ware Arbeitskraft als Basispreis festzulegen. Deshalb wird hiermit der Preis preisa der Ware Arbeitskraft während eines Reproduktionszyklus als bekannt angenommen. In meinen dimensionslosen Berechnungen wird er meist mit preisa=1 festgesetzt.

Jetzt können die ersten (n3-n5) Gleichungen für die Berechnung optimaler Preise preisw_i3 gemäß der 2.Annahme formuliert werden. Die wertmäßige Output-Input-Bilanz der (n3-n5) Unternehmen ii2, die an der optimalen Wirtschaftsstruktur beteiligt sind, lautet

mit

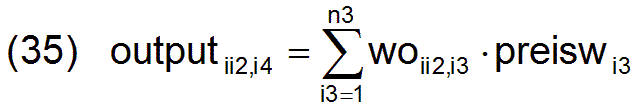
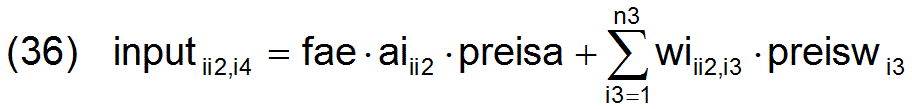
Durch Einfügen der Gleichungen (35), (36) und (7) in die Gleichung (34) und Umformen ergeben sich die (n3-n5) Gleichungen

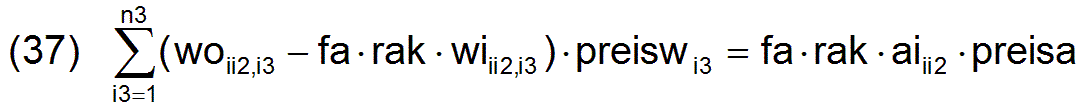
für (n3-n5) verschiedenen ii2

Da deponierte Abfälle der n5 Waren ii3 frei verfügbar sind, haben diese Waren den Preis Null.

Damit haben wir bereits n3 Gleichungen zur Berechnung der n3 Preise preisw_i3 , obwohl noch die wertmäßige Output-Input-Bilanz des Konsums der Arbeiter gemäß der 3.Annahme zu berücksichtigen ist. Diese lautet

mit

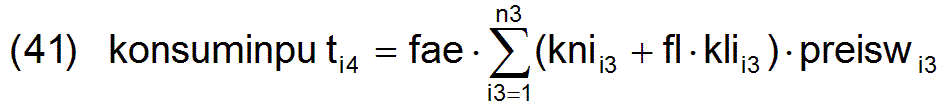
Durch Einfügen der Gleichungen (40), (41) und (7) in die Gleichung (39) und Umformen ergibt sich die Gleichung

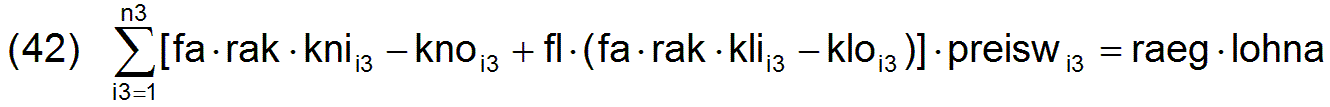
Der aufmerksame Leser wird sich hier wundern, wieso in Gleichung (37) mit dem Preis der Arbeitskraft preisa und in Gleichung (42) mit dem Lohn lohna des Arbeiters operiert wird, wieso die nicht identisch sind. Hier stoßen wir auf das Problem, welches den Notenbanken in der Regel Probleme bereitet, nämlich das Problem einer optimalen zirkulierenden Geldmenge innerhalb der Wirtschaft. Auch in diesem Modell würde die Missachtung dieses Sachverhalts zu Problemen führen. Es ist allerdings wegen der besserer Übersicht in diesem idealisierten Modell leichter zu lösen.

Wenn in meinem idealisierten Wirtschaftsmodell eine optimale Struktur herrscht, brauchen die Wirtschaftssubjekte keine finanziellen Rücklagen zu bilden. So können die Unternehmen zu Beginn des Reproduktionszyklus beim Einkauf der Produktionsmittel und der Arbeitskräfte ihre Finanzen voll verbrauchen. Auch die Arbeiter können zu Beginn des Reproduktionszyklus für den Kauf der Konsumgüter ihre Finanzen voll verbrauchen. So befindet sich am Ende eines Reproduktionszyklus nach der Lohnzahlung und vor dem Verkauf der Produkte an den zentralen Markt die gesamte minimal notwendige umlaufende Geldmenge in den Händen der Arbeiter, die sie gerade als Lohn erhalten haben und sie hat demnach das Volumen lohna* raeg* a. Falls ein Wirtschaftswachstum mit dem Faktor fae besteht und der Lohn konstant bleiben soll, so ist es notwendig, dass diese Geldmenge von Zyklus zu Zyklus ebenfalls um den Faktor fae wächst. Da im materiell-technischen Wirtschaftsprozess zwar Sachwerte aber kein Geld produziert wird, falls keine Fälscher am Werk sind, muss die Notenbank in entsprechender Menge Geld drucken und auf geeignete Weise in Umlauf bringen. In meinem Modell ist das die Menge (fae-1)* lohna* raeg* a.

Rechentechnisch lässt sich das in meinem Modell am leichtesten Realisieren, indem der Lohn der Arbeiter regelmäßig mit dem Faktor fae durch die Notenbank subventioniert wird. D.h., der Unternehmer zahlt für die Arbeitskraft den Preis preisa. Die Notenbank legt noch den Betrag (fae-1)* preisa drauf und der Arbeiter erhält den Lohn

Ob diese Geldeinspeisung durch Subventionierung d.h. Schenkung oder durch Darlehen erfolgt, ist für unsere Untersuchungen unerheblich.

Es soll allerdings noch darauf hingewiesen werden, dass die Stelle der Geldeinspeisung nicht notwendiger Weise beim Lohn erfolgen muss und nicht der Eindruck entstehen soll, dass der Arbeiter eigentlich nur einen Lohn in Höhe von preisa erarbeitet hat. Der Unternehmer als Eigentümer der Produktionsmittel hat sich ja die Menge der materiellen Produktion angeeignet und die Arbeiter sind gezwungen den notwendigen Anteil für die individuelle Konsumtion zurück zu kaufen und bei Bevölkerungs- und Wirtschaftswachstum auch den erweiterten Anteil. Man könnte auch annehmen, dass der Unternehmer den vollen Lohn an den Arbeiter zahlt, d.h. preisa=lohna. Dann müssten die Unternehmen regelmäßig mit der gleiche Geldmenge subventioniert werden, wenn trotz optimaler materiell-technischer Wirtschaftsstruktur das System nicht durch Geldmangel blockiert werden soll.

Es wäre allerdings auch möglich, die einmal vorhandene Geldmenge konstant zu lassen. Dann müssten bei Wirtschaftswachstum alle Preise ständig sinken. Das halte ich jedoch für unpraktisch.

Noch ein weiterer Hinweis: Dass die notwendige im Umlauf befindliche Geldmenge gleich dem Lohnvolumen sein muss, ist nicht prinzipiell der Fall, sondern liegt an der konkreten Art der Modellgestaltung. Hätte ich zum Beispiel den Gütermarkt nicht als einen zentralen (staatsnahen) Markt angenommen, der zum Kauf der Waren nach Bedarf problemlos auf Geld aus der Notenbank zurückgreifen kann, so würde sich das notwendige Geldumlaufvolumen erhöhen. Ein privatwirtschaftlich arbeitender Markt müsste nämlich ebenfalls zur Sicherung einer reibungslosen Geschäftstätigkeit mit einer ausreichenden Geldmenge ausgerüstet werden. Bei Wirtschaftswachstum müsste die ebenfalls regelmäßig aufgestockt werden.

Zurück zu unserem eigentlichen Thema dieses Abschnitts der Berechnung optimaler Preissysteme: indem wir Gleichung (43) in Gleichung (42) einsetzen erhalten wir die Gleichung

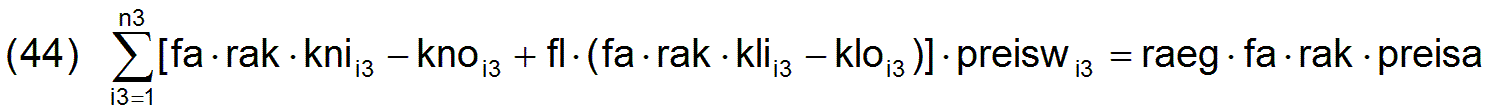
Damit haben wir ein lineares Gleichungssystem mit n3 Unbekannten und n3+1 Gleichungen. Testrechnungen haben gezeigt, dass es trotzdem regelmäßig eine eindeutige Lösung gibt. Die ersten (n3-n5) Gleichungen sind wohl linear abhängig und man kann eine davon weglassen und später eventuell zur Probe verwenden. Dafür, dass das so sein muss, gibt es sicher auch eine mathematische Erklärung, der ich bisher aber noch nicht nachgegangen bin. Die Gleichung (43) oder eine der n5 primitiven Gleichungen (38) darf nicht aus dem Gleichungssystem gestrichen werden.

Ein spezielles Problem der Preisfestlegung besteht noch bei den natürlichen Ressourcen, die der Natur entnommen werden und nicht durch den Menschen produziert werden können. In der kapitalistischen Marktwirtschaft, wo Privateigentum an natürlichen Ressourcen selbstverständlich ist, ist auch die Annahme üblich, dass es für die natürlichen Ressourcen einen sinnvollen Preis>0 gibt, der sich durch Angebot und Nachfrage einstellen soll. Das ist nach meinem bisherigen Erkenntnisstand nicht der Fall. Wenn in den oben entwickelten Gleichungen der Preis einer Ware auftritt, die benutzt, aber weder produziert noch verbraucht wird, und ich versuche das Gleichungssystem zu lösen, meldet das Berechnungsverfahren, dass es keine eindeutige Lösung gibt. Es muss also auch für nicht produzierbare Ressourcen ein Preis vorgeben werden. Prinzipiell ergibt jeder Preis eine Lösung. Wenn der Preis aber nicht mit Null angegeben wird, gibt es u.a. wieder Probleme mit den Geldmengen, ähnlich wie beim Lohn, nur komplizierter. Ich bin zu der Auffassung gekommen, dass es sinnvoll ist Ressourcenpreise ebenfalls Null zu setzen und werde zukünftig so verfahren. Die Gründe und daraus resultierenden Konsequenzen müssen zu einem späteren Zeitpunkt ausführlich dargelegt werden.

Damit ist das Problem der Berechnung einer optimalen Preisstruktur gelöst. Die Eindeutigkeit der Lösung des Gleichungssystems zeigt auch, dass es jeweils nur eine optimale Preisstruktur für eine optimale materiell-technische Wirtschaftsstruktur gibt. Andererseits kann es aber für einen Entwicklungsstand der Produktivkräfte mehrere optimale Wirtschaftsstrukturen geben, für die sich die Gesellschaft relativ frei entscheiden könnte, sofern sie die bewusste Organisation ihrer Produktionsverhältnisse beherrscht. Zu jeder dieser optimalen Wirtschaftsstrukturen gibt es dann eine andere optimale Preisstruktur.