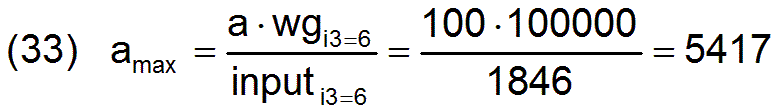
4.3 Die optimale Wirtschaftsstruktur für den speziellen Fall der Vollversorgung rak=1, Vollbeschäftigung reag=1 und ohne Bevölkerungswachstum fa=1
Der skizzierte Lösungsweg wurde in einem Programm mit Hilfe der Programmiersprache TurboPascal auf einem PC programmiert, so dass der Sachverhalt hier anhand des bereits oben definierten Demonstrationsbeispiels illustriert werden kann.
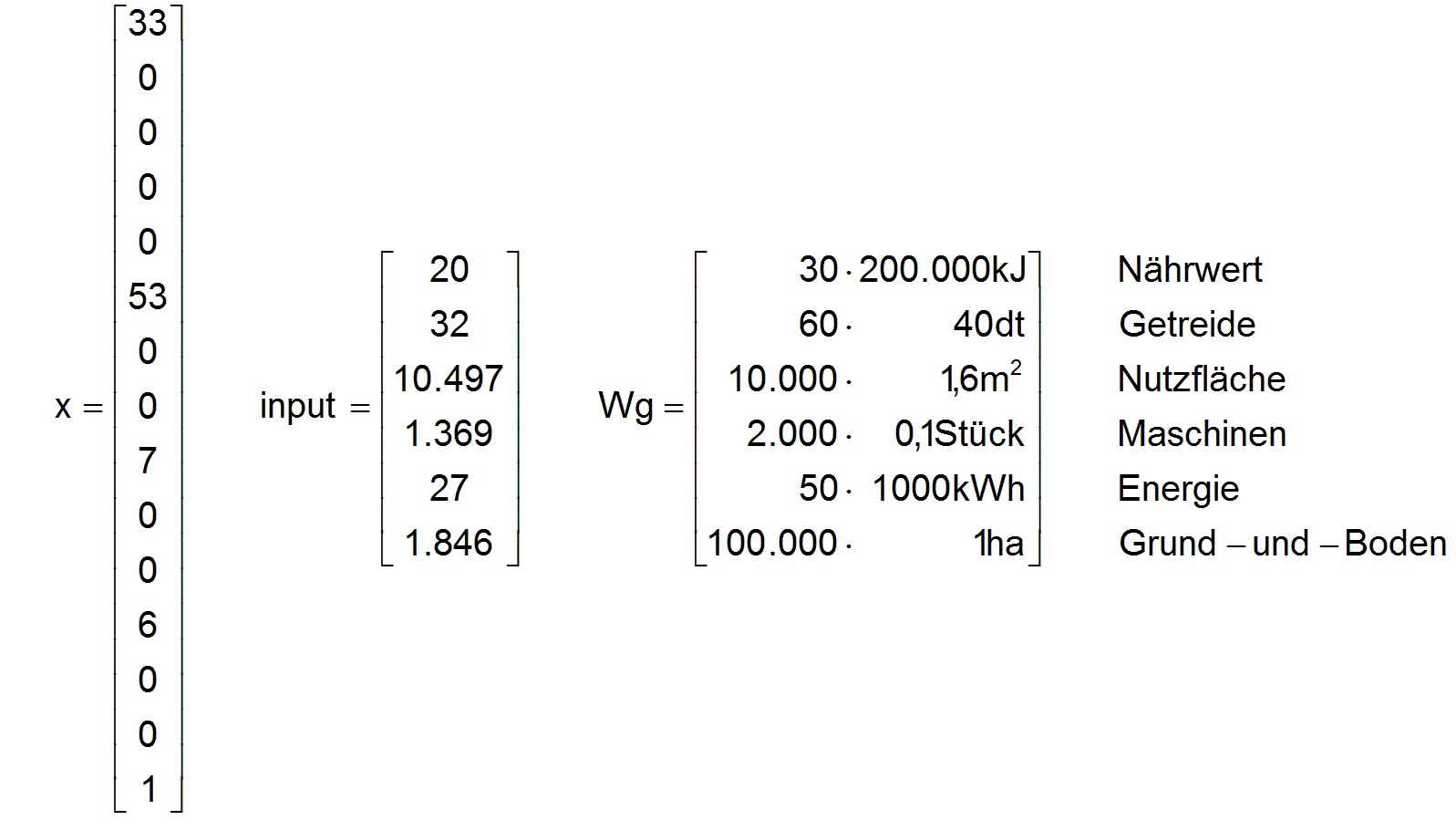
Für eine Anzahl von a=100 Beschäftigten ergibt sich eine optimale bedarfsgerechte Wirtschaftsstruktur mit den Produktionsvolumina x unter den Bedingungen, dass Vollversorgung ak=100 und Vollbeschäftigung aeg=100 verbindlich festgelegt wurde und dazu ein Maximum eines bedarfsgerechten Sortiments an zusätzlichen Konsumgütern angestrebt wurde, was durch den Faktor fl= 0,677 zum Ausdruck kommt.

Um die Produktion und den Konsum bedarfsgerecht realisieren zu können, ist das Gütersortiment input notwendig. Wg ist kein Ergebnis der Optimierung sondern war als externer Vektor bereits vorgegeben. Er wird hier zur Diskussion des Ergebnisses noch einmal in anschaulicher dimensionsbehafteter Form wiedergegeben.
Nehmen wir nun an, dass bisher nicht optimal gewirtschaftet wurde, so dass das verfügbare gesamtgesellschaftliche Gütersortiment wg mehr oder weniger zufällig ist, im Vergleich zu dem bedarfsgerechten Güterinput. Ein erster Blick zeigt, dass bei der Warenart i3=3, den Gebäuden, der erforderliche Wareninput inputi3=3 größer ist als die verfügbare Gütermenge wgi3=3 . Das bedeutet, dass in unserem Demonstrationsbeispiel nicht von Anfang an eine optimale Wirtschaftsstruktur möglich ist. Es müsste erst durch eine zeitweilige Mehrproduktion von Gebäuden für ein optimales Gütersortiment gesorgt werden. Da bei anderen Waren ein Überschuss vorhanden ist, könnte dieser eventuell zum Ausgleich zeitweilig mehr verbraucht werden.
Es kann auch die Frage beantwortet werden, wie viele Arbeiter könnten bei dem zur Zeit verfügbaren Gütersortiment wg optimal versorgt werden mit notwendigen und zusätzlichen Konsumgütern, ohne die optimale Wirtschaftsstruktur zu gefährden. Das knappste Gut sind z.Z. die Gebäude i3=3 mit dem geringen Defizit von 5%
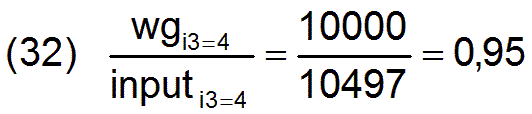
Die Anzahl der Beschäftigen könnte also nur 95 statt 100 betragen.
Es gibt ein Gut, welches zwar nicht verbraucht wird, aber auch nicht produziert werden kann, nämlich der Grund und Boden i3=6. Das stellt bei unveränderlicher Produktivität eine Wachstumsgrenze der Wirtschaft und der Bevölkerung dar. Damit ergibt sich die Frage, wie viele Arbeiter können langfristig maximal durch diese optimale Wirtschaftsstruktur beschäftigt und versorgt werden, nachdem über ein entsprechendes Bevölkerungswachstum und analoges Wirtschaftswachstum die Bevölkerungszahl maximiert wurde. Diese Zahl amax ergibt sich aus