Die verbalen Aussagen zu den Optimierungskriterien einer Volkswirtschaft sind nun mathematisch zu formulieren und ein Lösungsverfahren zur Berechnung des Optimums entsprechend dieser Kriterien ist zu entwickeln. Dazu wird das diskrete lineare Modell angenommen.

Bezogen auf die Wirtschaftsprozesse sind folgende exogene Parameter vorgegeben:

• Eine aktuelle Anzahl a der Arbeitskräfte.
• Ein Vermehrungsfaktor fa der Arbeitskräfte pro Reproduktionszyklus bei Vollversorgung.
• Eine Struktur der Bedürfnisse, beschrieben durch die Vektoren des notwendigen Konsums kni und kno und die Vektoren des zusätzlichen Konsums kli und klo.
• n2 Produktionsverfahren, beschrieben durch den normierten Arbeitskräfte-Input-Vektor ai, die Matrix wi der normierten Produktionsmittel-Inputs und die Matrix wo der normierten Produktions-Outputs.

Da die rechentechnische Lösung des Problems mit Hilfe des Simplexalgorithmus erfolgt, wird die Formulierung darauf zugeschnitten.

Die Anzahl der reellen Zahlen x, die Lösung der linearen Optimierung, sind in unserem Fall zunächst der Vektor x einer optimalen Produktionsstruktur bestehend aus den n2 Komponenten x_i2 der Produktionsvolumina der n2 Produktionsverfahren i2. Als weiterer gesuchter Parameter kommt die Anzahl ak der versorgten Arbeiter hinzu, die im Simplexalgorithmus als weitere reelle Zahl

bezeichnet wird.

Damit besteht der gesuchte Lösungsvektor zunächst aus den n2+1 reellen Zahlen x_j . Diese sind auch alle größer oder gleich Null, wie es das Verfahren fordert, denn ein negatives Produktionsvolumen und/oder eine negative Anzahl versorgter Arbeiter sind nicht möglich.

In einer längerfristig optimalen Wirtschaft ist für jede Warenart i3 der gesamtgesellschaftliche Produktionsoutput des vorhergehenden Reproduktionszyklus i4-1 größer oder gleich dem gesamtgesellschaftlichen ProduktionsmitteI- und Konsumgüterinput des aktuellen Zyklus i4.

bezeichnet wird.

Durch Einführung weiterer Variablen x_n2+1+i3 ,die den produzierten Abfall in der Güterart i3 darstellen und die möglichst gegen Null gehen sollen, lässt sich die Ungleichung in eine Gleichung umwandeln, wie es der Simplexalgorithmus verlangt.

bezeichnet wird.

Der gesamtgesellschaftliche Produktionsmittel- und Konsumgüter-Input des aktuellen Zyklus i4 berechnet sich durch die Formel

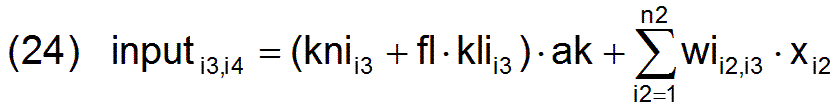
Der gesamtgesellschaftliche Produktions-Output des vorhergehenden Zyklus i4-1 berechnet sich durch die Formel

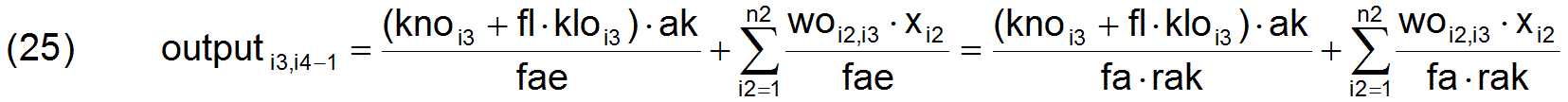
Dabei wird berücksichtigt, dass eine andauernd optimale Wirtschaft proportional mit dem tatsächlichen Vermehrungsfaktor fae wächst. Das heißt, dass jedes Produktionsvolumen des vorhergehenden Zyklus um den Faktor fae kleiner ist als das Produktionsvolumen x_i2 des aktuellen Zyklus. Außerdem gilt, wie oben bereits gezeigt, fae=fa·rak .

Damit kann die Gleichung (23) durch Einsetzen der Gleichungen (24) und (25) konkretisiert werden. Nach Umformung ergibt sich die folgende lineare Gleichung

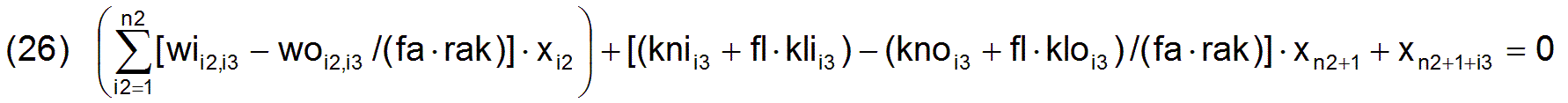
Diese Gleichung gilt für alle Warenarten i3= 1 bis n3 . Damit sind n3 lineare Nebenbedingungen für den Simplexalgorithmus gegeben, bei denen die Variablen x die zu optimierenden Parameter sind.

x_i2 für i2 = 1 bis n2 sind die gesuchten optimalen Produktionsvolumina.

x_n2+1 = ak ist die Anzahl der mit Konsumgütern versorgten Arbeiter.

x_n2+1+i3 für i3 = 1 bis n3 sind die zu minimierenden Abfallmengen in den n3 Warenarten.

Normalerweise streben wir Vollbeschäftigung an und so würde eine weitere Nebenbedingung lauten

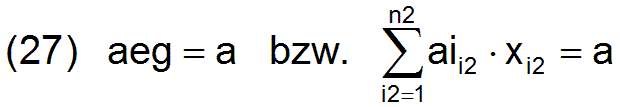
Da es aber auch Fälle geben kann, wo keine Vollbeschäftigung vorhanden ist, formulieren wir diese Nebenbedingung etwas allgemeiner, so dass auch der Fall einer Nichtvollbeschäftigung untersucht werden kann.

Die allgemeinere Formulierung der Nebenbedingung lautet dann: Die Anzahl aeg der beschäftigten Arbeiter ist gleich Beschäftigungsrate raeg mal Anzahl a der Arbeiter.

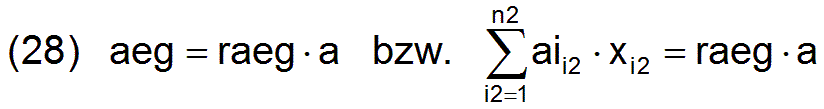
Diese Formulierung der Nebenbedingung wird nachfolgend allgemein verwendet. Sie enthält die Formulierung (27) als Sonderfall mit raeg=1.

In einer weiteren Nebenbedingung formulieren wir die Bedingungen der Versorgung der Bevölkerung: Es wird Vollversorgung gefordert, d.h.

Das ist wieder die strengere Formulierung. Um auch Fälle untersuchen zu können, wo mal keine Vollversorgung möglich ist, wird allgemeiner formuliert: Die Anzahl ak der mit Konsumgütern versorgten Arbeiter ist gleich Versorgungsrate rak mal Anzahl a der Arbeiter.

Damit gibt es jetzt insgesamt n3+2 Nebenbedingungen.

Zielfunktion:

Es soll möglichst wenig Abfall produziert werden.

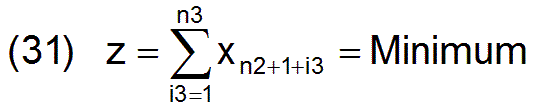
Damit ist das lineare Optimierungsproblem vollständig beschrieben. Wenn wir die drei Optimierungskriterien einer Volkswirtschaft noch einmal ansehen, stellen wir fest, dass das dritte Kriterium der Bedarfsgerechtigkeit in den ersten n3 Nebenbedingungen (26) und in der Zielfunktion (31) verankert ist. Das erste Kriterium der Versorgung, in der Regel Vollversorgung mit rak=1, ist in der letzten Nebenbedingung (30) formuliert. Hinzu kommt mit der vorletzten Nebenbedingung (28) auch noch eine Aussage zur Beschäftigung.

Das zweite Kriterium der maximalen Versorgung mit zusätzlichen Konsumgütern ist aber bisher nicht berücksichtigt. Dieses Kriterium erfordert die Maximierung des Faktors fl. Da er aber gemeinsam mit x_n2+1 in einem Glied auftritt kann er nicht als Variable des Lösungsvektors x innerhalb der linearen Optimierung behandelt werden.

Es wird nun in folgender Weise vorgegangen: Zunächst wird der minimale Wert fl=0 angenommen und durch lineare Optimierung mittels Simplexalgorithmus ein Optimum gesucht. Gibt es für diesen Punkt kein Optimum, dann ist für diesen Fall keine Lösung vorhanden, das heißt die Produktivkräfte sind prinzipiell überfordert und die Berechnung kann beendet werden. Gibt es eine Lösung für fl=0, kann durch weiteres systematisches probieren der maximale Faktor fl iterativ ermittelt werden, für den es gerade noch eine Lösung gibt, womit dann auch das zweite Kriterium erfüllt ist.