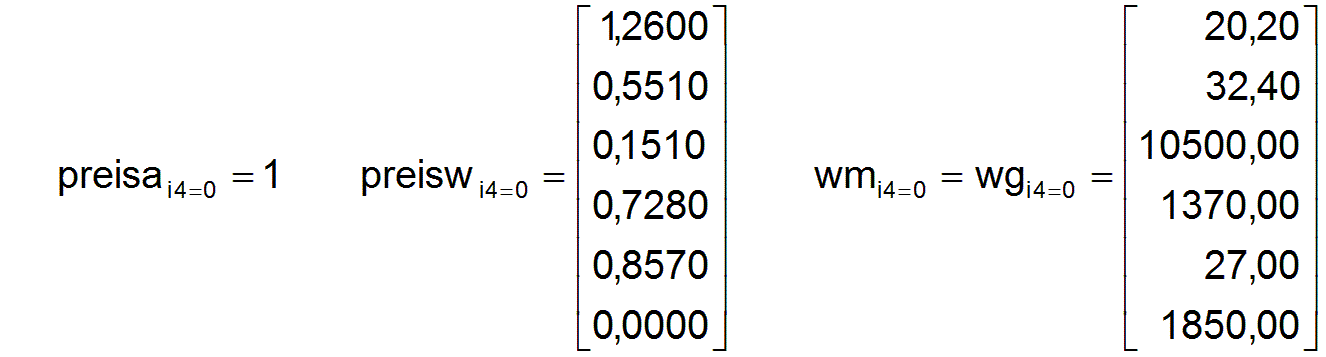
3.2 Testrechnungen mit dem Modell
Ziel der Übung Marktwirtschaft ist es ja bekanntlich, dass sich jeder Unternehmer nur um seinen Kram kümmert, d.h. um die rationelle Anwendung seines Produktionsverfahrens, um daraus maximalen Gewinn zu erzielen. Durch die Marktwirtschaft soll sich dann über die Regelung der Preise in Abhängigkeit von Angebot und Nachfrage automatisch eine optimale d.h. bedarfsgerechte Wirtschaftsstruktur einstellen. Demnach müssten sich bei einer beliebigen Anfangssituation mit der Zeit optimale Verhältnisse einspielen, nach Ansicht der Monetaristen mit Vollbeschäftigung und nach Ansicht der Keynesianer wenigstens mit Teilbeschäftigung. Dass das in der real existierenden kapitalistischen Marktwirtschaft nicht der Fall ist, ist hinlänglich bekannt, wobei der Streit darum geht, ob das nun am System liegt oder ob sich die Beteiligten nur falsch verhalten und damit das Prinzip der Marktwirtschaft außer Kraft setzen.
Die Anwendung meines Modells ist ernüchternd. Bisher ist es mir nicht gelungen in einem einzigen einfachen Demonstrationsbeispiel zu zeigen, dass eine Selbstoptimierung stattfindet. Es ist sogar noch schlimmer. Wenn ich optimale Anfangsbedingungen annehme und mit diesen über einige Reproduktionszyklen weiterrechne, entfernt sich das System allmählich immer mehr vom Optimum, bis chaotische Zustände eintreten. Ursache sind kleinste Abweichungen durch Rundungen der Anfangsparameter. Eine kapitalistische Marktwirtschaft gemäß meines Modells ist nicht selbstoptimierend, hat im Optimalzustand noch nicht einmal ein indifferentes Gleichgewicht, sondern ein instabiles Gleichgewicht.
Anhand unseres Demonstrationsbeispiels soll das einmal gezeigt werden.
Zu Beginn des ersten Reproduktionszyklus sind fast optimale Anfangswert gegeben. Die Abweichungen vom Optimum bestehen lediglich aus Rundungsfehlern. Hier wurden alle Parameter auf drei signifikante Ziffern gerundet.
Es ist ein fast optimales Preissystem bekannt, gegeben durch preisai4=0 und den Vektor preiswi4=0 und es stehen für die gesamtgesellschaftliche Nutzung die Warenmengen wmi4=0 =wgi4=0 auf dem Markt zum Verkauf bereit.
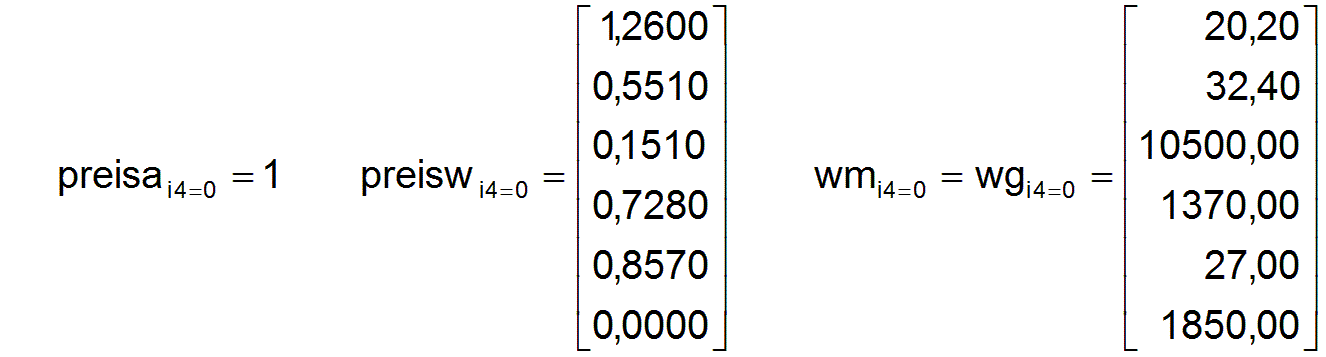
Die 100 Arbeiter haben eine Geldmenge geldaai4=0=667, die ausreichend ist, um Waren zu den aktuellen Preisen in einem bedarfsgerechten Sortiment zu kaufen, um sich damit im kommenden Reproduktionszyklus vollständig zu versorgen, wobei ein fast optimaler Faktor fl=0,677 des zusätzlichen Konsums berücksichtigt ist.
Alle an einer optimalen Produktionsstruktur beteiligten Unternehmen i2 besitzen eine ausreichende Menge Geldkapital geldui2,i4=0 ,um ein bedarfsgerechtes Sortiment an Produktionsmitteln wui2=xi2* wii2 zu kaufen, mit dem sie ein für die gesamte Gesellschaft optimales Volumen an neuen Waren produzieren können. Der Vektor geldu der Geldmengen geldui2 aller n2 Unternehmen i2 ist gegeben durch
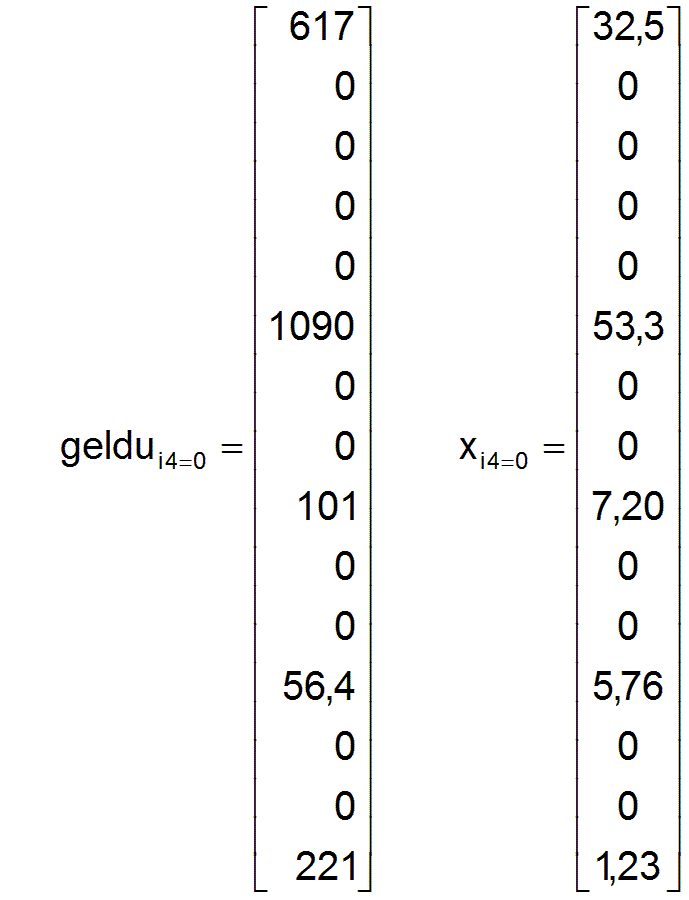
Diese Parameter ergeben die oben angegebene fast optimale Wirtschaftsstruktur xi4=1 im ersten Reproduktionszyklus.
Der Faktor f2, der die Geschwindigkeit der Preisanpassung beeinflusst, und der Faktor f4, der das Streben des Marktes nach einer Warenreserve beeinflusst, wurden mit folgenden Werten belegt.
f2 = 0,5 f4 = 2
Bild 1 zeigt die Preisentwicklung über 50 Reproduktionszyklen. Anstatt annähernd konstant zu bleiben, was anfänglich auch der Fall ist, schaukeln sie sich auf.
Das führt zu erheblichen Schwankungen der Unternehmergewinne, die in Bild 2.1 durch die Gewinnfaktoren fgewinnu0i2 für Unternehmen i2= 1 bis 15 über 50 Reproduktionszyklen dargestellt sind. Die Gewinnfaktoren sind definiert durch
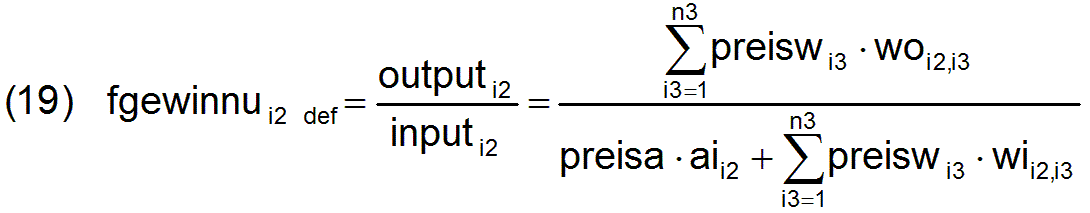
Es handelt sich hier also um die Gewinne bezogen auf die tatsächlich in die Produktion eingegangenen Werte und nicht bezogen auf das gesamte Vermögen der Unternehmen. Es wurden die Gewinnfaktoren aller 15 Unternehmen ermittelt. Für die Unternehmen, die nicht an der Produktion beteiligt sind, wurden die theoretischen Gewinnfaktoren in gleicher Weise berechnet.
Bild 2.2
zeigt die Gewinnfaktoren noch einmal über die ersten 20 Reproduktionszyklen mit einer größeren Auflösung. Hier ist zu erkennen, dass zu Beginn die Gewinnfaktoren mehrerer Unternehmen exakt bei Eins liegen, wie sich das für die Gewinnfaktoren der 5 Unternehmen gehört, die an der optimalen Wirtschaftsstruktur ohne Wachstum (fa=1) mit einem Produktionsvolumen beteiligt sind. Alle anderen nicht konkurrenzfähigen Unternehmen haben Gewinnfaktoren kleiner Eins. Es ist außerdem zu erkennen, dass durch die Instabilität der Preise die Gewinnfaktoren sofort zu streuen beginnen.Bild 3
zeigt, dass es mit den Wachstumsfaktoren fae und fwi3 ähnlich aussieht, obwohl diese alle wegen des Bevölkerungswachstums fa=1 auch annähernd Eins sein müssten und gegen exakt Eins konvergieren müssten. Die Warenwachstumsfaktoren sind definiert durch![]()
Daraus resultierend kommt es zu Disproportion in der Wirtschaftsstruktur, die zu Warenengpässen und damit zu Produktionsausfällen führen. Diese führen zum Rückgang Beschäftigungszahlen aeg, zu Einkommensausfällen der Arbeiter . Dadurch kommt es zu Unterversorgung der Bevölkerung (ak<a) und damit zum Rückgang der Bevölkerungszahl a, wie in Bild 4 zu sehen ist.
Verschiedene Testrechnungen haben gezeigt, dass eine Veränderung der Faktoren f2 und f4 nur die Geschwindigkeit der Entwicklung des wirtschaftlichen Chaos verändern. Die Instabilität bleibt bestehen. Auch eine Verbesserung der Genauigkeit der Anfangswerte verzögert nur die Entstehung des Chaos, hält sie aber prinzipiell nicht auf.
zurück weiter