2.2 Demonstrationsbeispiel
An einem kleinen Demonstrationsmodell sollen nun die vorangegangenen Ausführungen illustriert werden. Dieses Demonstrationsbeispiel wird mit einigen Variationen und Ergänzungen fast durchgängig zur Illustration meiner Ausführungen benutzt. Es wird aber darauf hingewiesen, dass die angegebenen Werte in ihrer Auswahl und Größe willkürlich festgelegt wurden und eine annähernde Übereinstimmung mit tatsächlichen Verhältnissen nicht angestrebt wurde, weil sie bei einer derart geringen Anzahl von ausgewählten Gütern und Produzenten prinzipiell nicht möglich ist. Es geht um das Prinzip.
Der synchrone Reproduktionszyklus sei mit einer Dauer von einem Monat festgelegt.
Es gibt 100 arbeitsfähige Mitglieder (Arbeiter) der Gesellschaft, d.h. a=100.
Es sollen alle Arbeiter einschließlich ihrer Kinder mit den notwendigen Lebensmitteln versorgt sein, d.h. ak=100.
Geburtenrate und Sterberate sind ausgeglichen, d.h. fa=1.
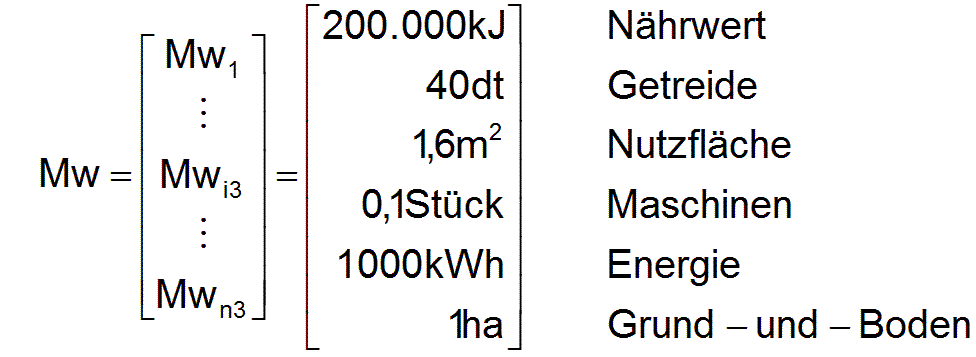
Es gibt 6 Güterarten, die in den entsprechenden Einheiten erfasst werden:
| i3 | Güterart | Maßeinheit bzw. | Normal |
|---|---|---|---|
| 1 | Brot/Backwaren | 200.000 | kJ |
| 2 | Getreide | 40 | dt |
| 3 | Gebäude | 1,6 | m2 |
| 4 | Maschinen | 0,1 | Stück |
| 5 | Energie | 1000 | kWh |
| 6 | Grund und Boden | 1 | ha |
Damit ist der Vektor Mw der Maßeinheiten bzw. Normale gegeben durch

In diesen Maßeinheiten werden nachfolgend alle Güterarten in den verschiedenen Vektoren und Matrizen dargestellt.
Ein Arbeiter benötigt für sich und seine Kinder während des Reproduktionszyklus von einem Monat Brot mit einem Nährwert von 20.000 kJ (hier stellvertretend für alle Nahrungsmittel) und Energie von 50 kWh. Er benötigt Wohnraum von mindestens 25* 1,6=40 m2 auf einem Grundstück von anteilig mindesten 1 ha. Das Wohnhaus hat einen Verschleiß von 12% pro Reproduktionszyklus. Der Grund und Boden verschleißt nicht. Damit kann der notwendige Input und Output an Konsumgütern für einen Arbeiter und einen Reproduktionszyklus angegeben werden.
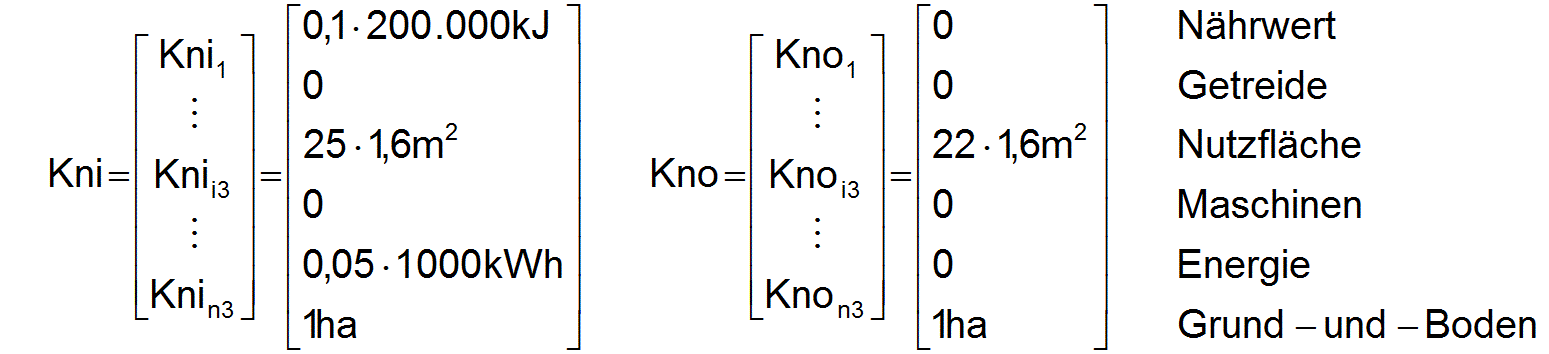
Bei einem entsprechenden zusätzlichen Konsumgüterangebot würden die Arbeiter mehr Lebensmittel und mehr Energie verbrauchen, in einer größeren Wohnung auf einem größeren Grundstück wohnen. Aufgrund statistischer Erhebungen könnte sich dabei folgende gewünschte Struktur des nicht notwendigen Konsums als Mittelwert für die gesamte Gesellschaft ergeben
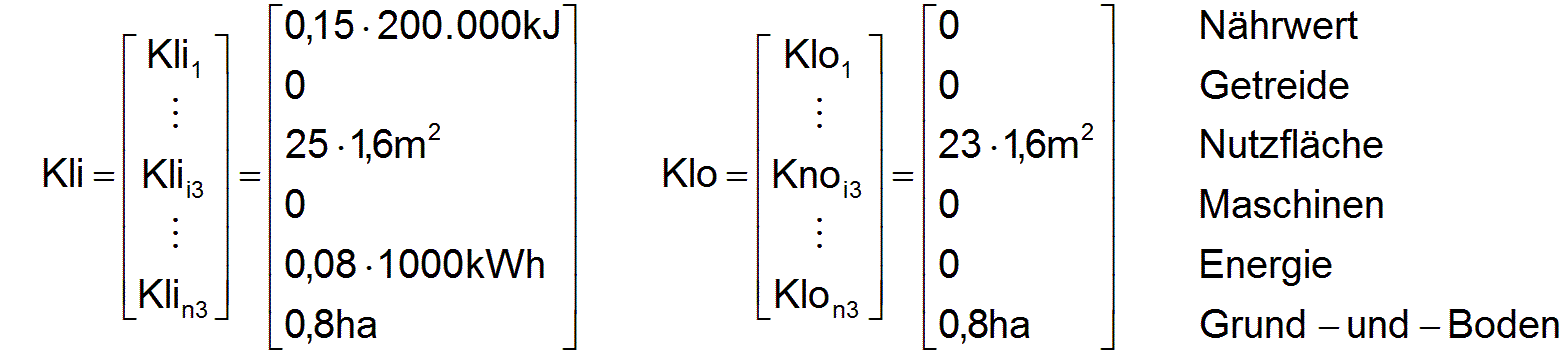
Durch Abspalten der Maßeinheit bzw. des Normales werden nun die vier Vektoren dimensionslos gemacht.
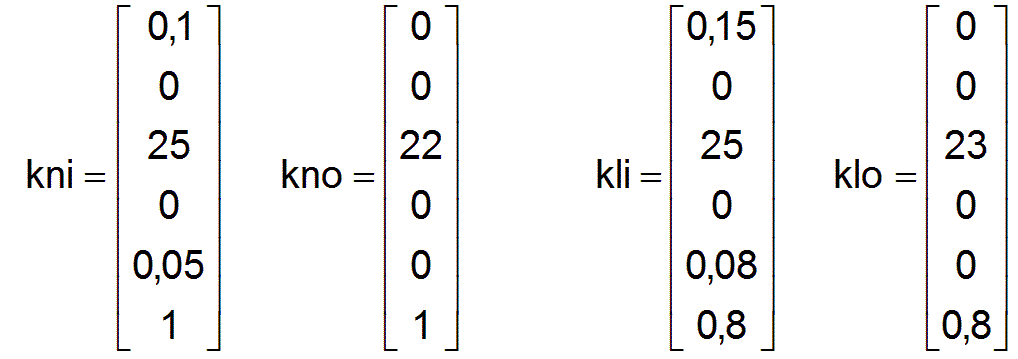
Alle Werte in den folgenden Vektoren und Matrizen werden analog dimensionslos gemacht und werden zukünftig sofort dimensionslos dargestellt.
Es sind nun die Produktionsverfahren bzw. Unternehmen zu beschreiben.
Das erste Unternehmen i2=1 sei eine Maschinenfabrik. Zur Produktion werden Arbeitskräfte ai1 , Gebäude wi1,3 , Maschinen wi1,4 ,Energie wi1,5 und ein Grundstück wi1,6 benötigt, die den Produktionsmittelinput wi1 darstellen. Der Produktionsoutput wo1 besteht aus den produzierten Maschinen und den Produktionsmaschinen unter Berücksichtigung eines abzuschreibenden Verschleißes. Beides zusammen ergibt den Parameter wo1,4 . Dazu kommen die verbleibenden Gebäude wo1,3 und das Grundstück wo1,8 . Da es sich um ein linearisiertes Modell handelt, bei dem die Abhängigkeit der Produktivität von der Betriebsgröße vernachlässigt wird, werden der Inputvektor und der Outputvektor auf ein Produktionsvolumen von einer Arbeitskraft normiert. Damit könnte das Produktionsverfahren des Unternehmens i2=1 durch den Parameter ai1 und die beiden bereits dimensionslosen Zeilenvektoren wi1 und wo1 beschrieben werden:
| i3: | 1 | 2 | 3 | 4 | 5 | 6 | |||
| ai1=1 | wi1 | = [ | 0 | 0 | 70 | 10 | 0,15 | 3] | |
| wo1 | = [ | 0 | 0 | 63 | 13 | 0 | 3] |
In Worten bedeuten diese Vektoren, dass in einem Monat in einem Fabrikgebäude mit einer Produktionsfläche von 70* 1,6=112 m2, mit 10* 0,1=1 Stück Maschine, einem Energieverbrauch von 0,15* 1000=150 kWh auf einem Grundstück von 3 ha produziert ein Arbeiter (13-10)* 0,1=0,3 Maschinen.
In analoger Weise wurden 14 weitere Produktionsverfahren beschrieben und die 15 Zeilenvektoren wii2 und woi2 zu den Matrizen wi und wo und die Parameter aii2 zu dem Vektor ai zusammengefasst.
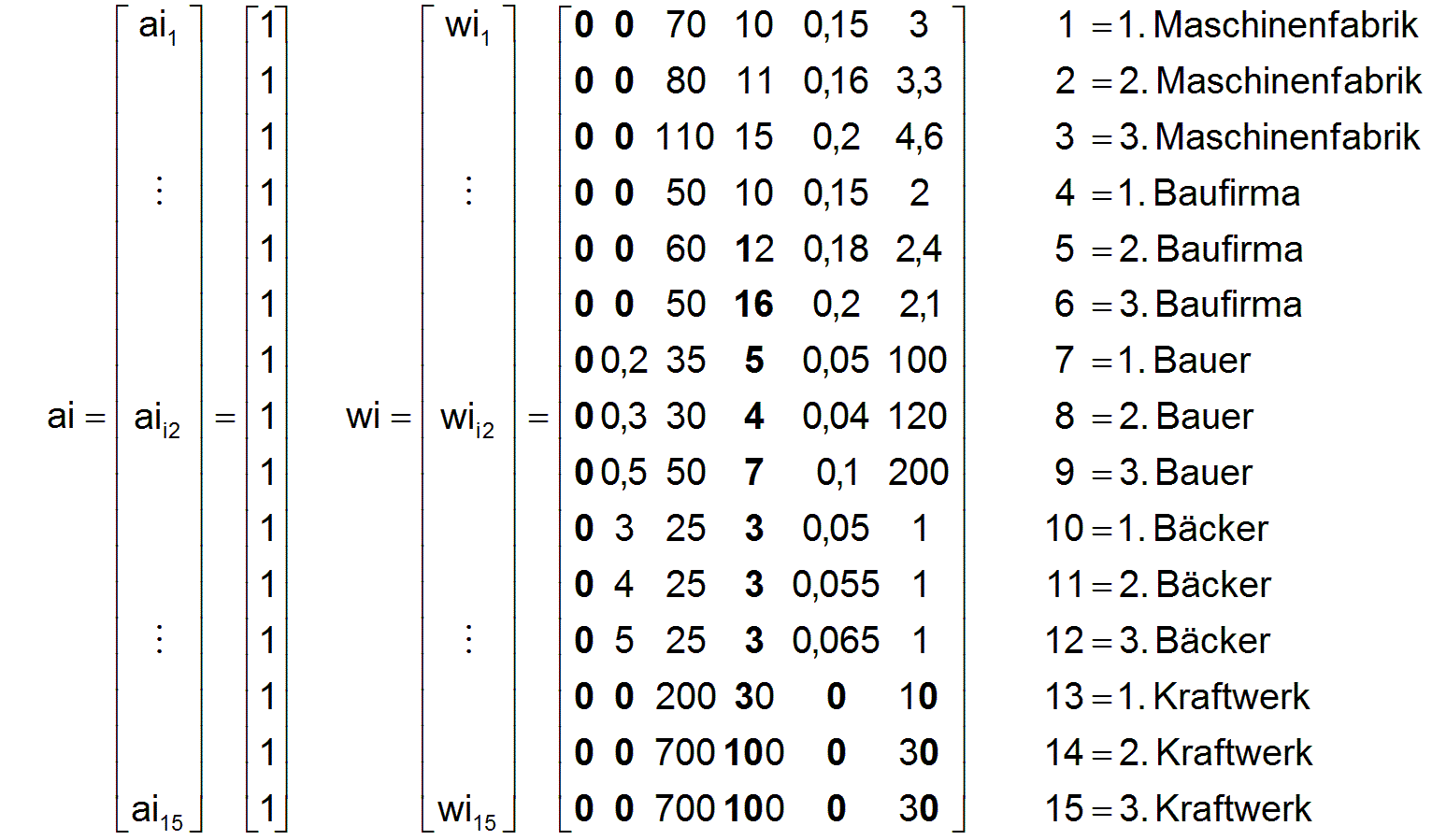
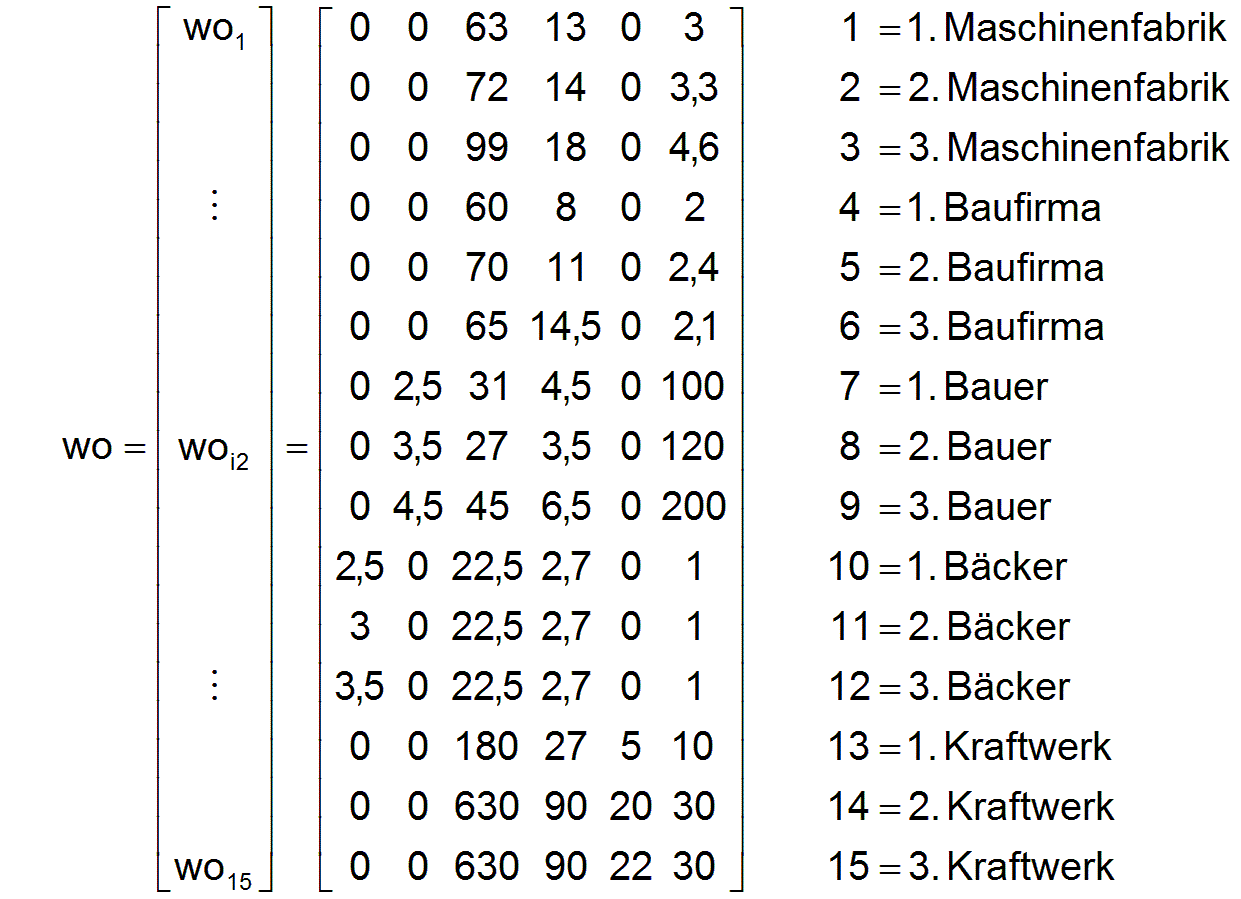
Entsprechend den festgelegten Parametern sind die ersten drei Unternehmen i2= 1 bis 3 Maschinenfabriken mit unterschiedlicher Produktivität. Die Unternehmen i2= 4 bis 6 sind Baufirmen. Die Unternehmen i2= 7 bis 9 sind Bauern. Die Unternehmen i2= 10 bis 12 sind Bäcker und die Unternehmen i2= 13 bis 15 sind Kraftwerke.
Zum Schluss werden noch die aktuell verfügbaren Gütermengen wg in dimensionslosen Werten angegeben. Sie stehen als Konsumgüter oder als Produktionsmittel zur Verfügung:
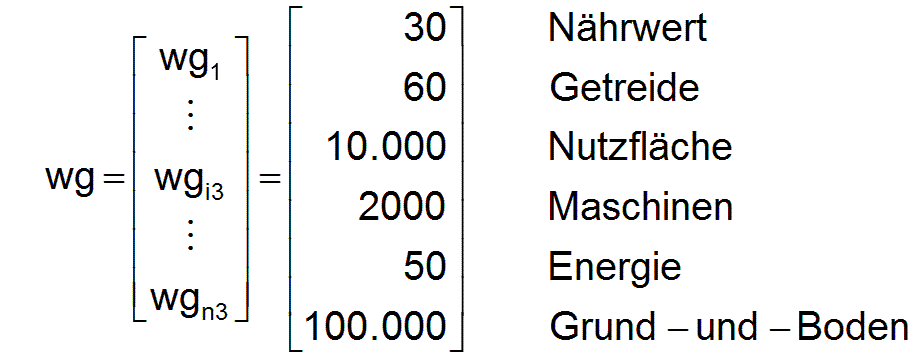
Dieses verfügbare Gütersortiment muss zunächst nicht bedarfsgerecht sein.
Zur vollständigen Beschreibung aller primären Parameter des materiellen Wirtschaftsgeschehens fehlen jetzt noch der Vektor x der Produktionsvolumina und der Faktor fl des nicht notwendigen Konsums. Diese hängen von den jeweiligen Produktionsverhältnissen ab, die die Menschen eingehen. Die Qualität der Produktionsverhältnisse ist danach zu bewerte, in welchem Maße die Produktionsverhältnisse bewirken, dass sich optimale Reproduktionsstrukturen ergeben. Sowohl die kapitalistische Marktwirtschaft, als auch die untergegangene "real existierende" sozialistische Planwirtschaft haben bisher offenbar nicht das Optimum erreicht bzw. halten können.
zurück weiter