zurück weiter
2.1 Ein lineares Modell mit diskreten synchronen Reproduktionszyklen
Reproduktionszyklen:
- Der Reproduktionsprozess der Gesellschaft erfolgt in diskreten gleichlangen Zeitabschnitten Tz, die Reproduktionszyklen genannt werden. Die Aktivitäten aller Wirtschaftssubjekte erfolgen synchron innerhalb dieser Reproduktionszyklen. Das betrifft die Produktion, den individuelle Konsum und andere Aktivitäten. Die Reproduktionszyklen werden mit dem Index i4 durchnummeriert.
Ressourcen der Gesellschaft:
- Die Gesellschaft besteht aus der Anzahl von a Mitgliedern.
- Alle Mitglieder der Gesellschaft sind arbeitsfähig, so dass im Reproduktionszyklus ein Arbeitsvermögen von a Arbeitskräften zur Verfügung steht. Im aktuellen Zyklus nicht genutztes Arbeitsvermögen geht verloren. Es kann nicht für später aufgespart werden.
- Es existieren n3 verschiedene Arten von Gütern, die mit dem Index i3= 1 bis n3 durchnummeriert sind. Diese Güter können natürliche Ressourcen, wie Grund und Boden, Bodenschätze, Sonnenenergie oder gewachsene Rohstoffe sein. Es können Produktionsmaschinen, Material und halbfertige Produkte sein. Es können Güter und Dienstleistungen sein, die für den individuellen Konsum bestimmt sind.
- Die Gesellschaft verfügt aktuell über die Gesamtmengen Wg an Wirtschaftsgütern. Dieses Gütersortiment ist ein Vektor bestehend aus den n3 Komponenten Wgi3 . Es ist zu beachten, dass jede Güterart in ihrer für sie spezifischen Maßeinheit quantifiziert wird und auf keinen Fall in einem Geldwert.
- Es wird angenommen, dass alle Güter bis zu ihrem Verbrauch unbegrenzt lagerfähig sind.
Produktionsverfahren und produzierende Wirtschaftseinheiten:
- Es existieren n2 Produktionsverfahren, die mit dem Index i2= 1 bis n2 durchnummeriert sind. Dazu zählen alle derzeit bekannten Verfahren, auch wenn sie momentan nicht angewendet werden.
- Das Produktionsverfahren i2 wird in folgender Weise als Blackbox dargestellt: Wenn ein bedarfsgerechtes Gütersortiment Wii2 , der Produktionsmittelinput, zu Beginn eines Reproduktionszyklus bereitgestellt wird und eine Anzahl von aii2 Arbeitern über den Zeitraum dieses Reproduktionszyklus damit beschäftigt wird, das Produktionsverfahren i2 auf das Gütersortiment anzuwenden, ist das Gütersortiment Wii2 am Ende des Reproduktionszyklus in das Gütersortiment Woi2, den Produktionsoutput, übergegangen. Der Produktionsmittelinput Wii2 ist ein Vektor bestehend aus den n3 Komponenten Wii2,i3 . Der Produktionsoutput Woi2 ist ein Vektor bestehend aus den n3 Komponenten Woi2,i3 .
- Es wird angenommen, dass jedes Vielfache xi2 des Parameters aii2 und der Vektoren Wii2 und Woi2 das gleiche Produktionsverfahren lediglich mit einem anderen Produktionsvolumen xi2 darstellt. Damit ist ein linearer Ansatz der Produktionsfunktion gegeben. Der Parameter aii2 und die Vektoren Wii2 und Woi2 sind die Basiswerte des Verfahrens, die entsprechend dem zugehörigen Produktionsvolumen xi2 =1 ein normales bzw. normiertes Volumen darstellen. Deshalb werden diese Parameter aii2 und die Vektoren Wii2 und Woi2 in Zukunft als normierte Parameter bzw. Vektoren bezeichnet. Die Normierung erfolgt in der Regel in der Weise, dass aii2 =1 gesetzt wird.
- Die Gesamtzahl der beschäftigten Arbeiter soll mit aeg bezeichnet werden. Sie ist definiert durch
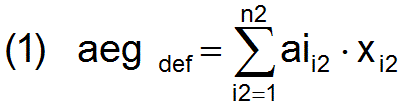
- Ergänzend wir nun noch der Begriff der Beschäftigungsrate raeg eingeführt. Sie ist definiert durch
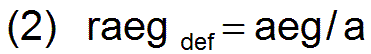
- Alle aii2 der n2 Produktionsverfahren kann man zu einem Vektor ai zusammenfassen und alle Vektoren Wii2 und Woi2 kann man zu den Matrizen Wi und Wo zusammenfassen, in folgender Weise
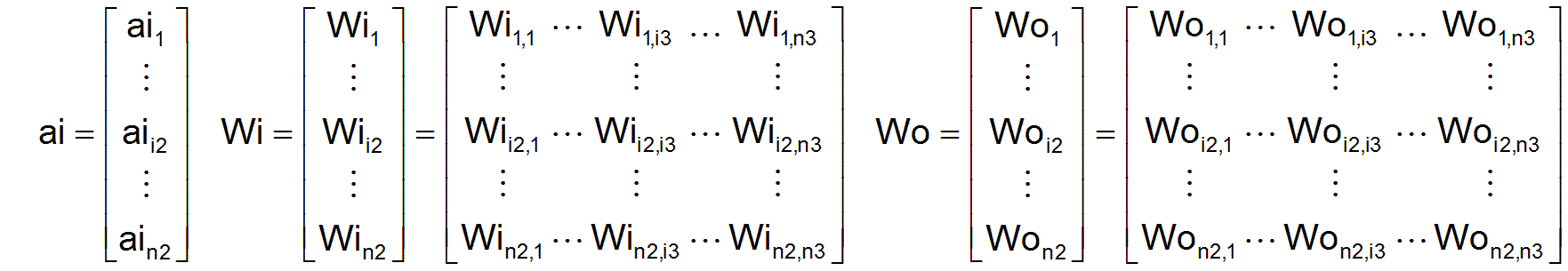
Damit sind alle n2 Produktionsverfahren durch ai, Wi und Wo vollständig beschrieben.
- Das Produktionsverfahren i2 dargestellt durch aii2 ,Wii2 und Woi2 und ein dazugehöriges Produktionsvolumen xi2>0 beschreibt die produzierende Wirtschaftseinheit i2 . xi2=0 bedeutet, dass das Verfahren i2 zwar bekannt ist und zur Anwendung zur Verfügung steht, aber z.Z. nicht benutzt wird und damit z.Z. eine produzierende Wirtschaftseinheit i2 nicht existiert.
Bedarf, Konsum und Vermehrung der Mitglieder der Gesellschaft (Arbeiter):
- Ein Arbeiter benötigt pro Reproduktionszyklus für den Erhalt seines Lebens, die Reproduktion seiner Arbeitskraft und die Versorgung seiner Kinder ein bedarfsgerechtes Gütersortiment, das mit Kni bezeichnet wird. Das ist ein Vektor bestehend aus den n3 Komponenten Knii3 ,die jeweils den Bedarf in der Warenart i3 darstellen. Dieser Vektor stellt analog dem Produktionsmittelinput einen Konsumgüterinput dar. Wird dem Arbeiter ein nicht bedarfsgerechtes Kosumgütersortiment zur Verfügung gestellt, kann nur der darin enthaltene bedarfsgerechte Anteil zum Konsum genutzt werden.
- Zum Konsumgüterinput kni wird der Konsumgüteroutput Kno definiert, bestehend aus den n3 Komponenten Knoi3 , der aus dem notwendigen Konsum resultiert. Dieser Vektor ist erforderlich, da während eines Reproduktionszyklus zwar das gesamte Konsumgütersortiment Kni zum Lebensunterhalt notwendig ist, dabei aber nicht unbedingt vollständig verbraucht wird, sondern manche Güter benutzt werden und dabei nur langsam oder gar nicht verschleißen.
- Es wird angenommen, dass alle Arbeiter den gleichen notwendigen Konsumtionsbedarf haben.
- Wird ein Arbeiter mit dem notwendigen bedarfsgerechten Konsumgütersortiment Kni versorgt, so reproduziert er seine Arbeitskraft und vermehrt sich um den Faktor fa pro Reproduktionszyklus. Wird ein Arbeiter nicht mit dem notwendigen bedarfsgerechten Konsumgütersortiment Kni versorgt, ist er am Ende des Reproduktionszyklus gestorben und die Anzahl der Arbeiter reduziert sich entsprechend. Dabei soll er aber im aktuellen Zyklus noch in der Lage sein, Arbeit zu leisten. Die Anzahl der mit den notwendigen Konsumgütern versorgten Arbeiter wird mit ak bezeichnet. Damit ist die Entwicklung der Bevölkerungszahl von einem Reproduktionszyklus zum nächsten durch folgende Beziehung gegeben
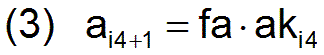
- Ergänzend wird der Begriff der Versorgungsrate rak eingeführt. Sie ist definiert durch

- Ist die Anzahl ak der versorgten Arbeiter kleiner als die Anzahl a der vorhandenen Arbeiter, so reduziert sich die Vermehrung der gesamten Bevölkerung vom Reproduktionszyklus i4 zum Zyklus i4+1 gegenüber dem maximalen Faktor fa auf den tatsächlich realisierten Vermehrungsfaktor fae, der definiert ist durch
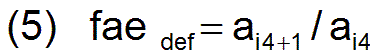
- Aus der Definition (5) und den Gleichungen (3) und (4) ergeben sich die folgenden Gleichungen für fae
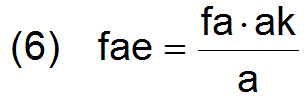
und
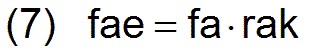
- Zusätzlich zu dem notwendigen Konsumgütersortiment können die Arbeiter auch mit einem Sortiment an nicht unbedingt notwendigen zusätzlichen Konsumgütern versorgt werden. Das können weitere nützliche und/oder subjektiv gewünschte Konsumgüter sein. Das schließt den Luxuskonsum ein, umfasst aber wesentlich mehr. Zur Verkürzung wird im folgenden nur noch von zusätzlichen Konsumgütern gesprochen. Der Vektor eines normierten bedarfsgerechten zusätzlichen Konsumgütersortiments (Konsumgüterinput) wird mit Kli bezeichnet. Es wird angenommen, wenn Kli für einen Arbeiter während eines Reproduktionszyklus ein bedarfsgerechtes zusätzliches Güterangebot ist, dass dann jedes Vielfache dieses Sortiments ebenfalls ein von ihm akzeptiertes Angebot ist, welches er konsumiert sofern es ihm zur Verfügung steht. Deshalb wird der Faktor fl eingeführt. Das Produkt aus fl* kli ergibt dann das für einen Arbeiter pro Reproduktionszyklus verfügbare zusätzliche, bedarfsgerechte Konsumgütersortiment.
- Ein zusätzliches Konsumgüterangebot fl* kli wird von einem Arbeiter aber nur konsumiert falls in diesem Reproduktionszyklus auch das notwendige Konsumgütersortiment kni zur Verfügung steht. Bei einem nicht bedarfsgerechten Angebot wird nur der darin enthaltene bedarfsgerechte Anteil konsumiert.
- Analog zu den bisherigen Definitionen wird der Vektor Klo, der normierte Konsumgüteroutput des zusätzlichen Konsums, definiert, bestehend aus den Komponenten Kloi3 . Dieser geht hervor aus dem Konsum (Benutzung und/oder Verbrauch) des Vektors Kli durch den Arbeiter und steht am Ende des Zyklus zur weiteren Verfügung.
- Es wird angenommen, dass alle Arbeiter die gleiche Bedarfsstruktur an zusätzlichen Konsumgütern haben.
Damit ist das System der Produktivkräfte einer Volkswirtschaft vollständig beschrieben. Zur Vereinfachung der rechentechnischen Modellierung werden noch die entsprechenden dimensionslosen Parameter eingeführt:
- Es wurde oben bereits darauf hingewiesen, dass jede Güterart in ihrer eigenen Maßeinheit bestimmt wird. Diese Maßeinheiten bzw. Normale werden in dem Vektor Mw zusammengefasst, der aus den n3 Komponenten Mwi3 besteht. Damit ergeben sich die entsprechenden dimensionslosen Parameter, die zur Unterscheidung beginnend mit einem kleinen Buchstaben bezeichnet werden:
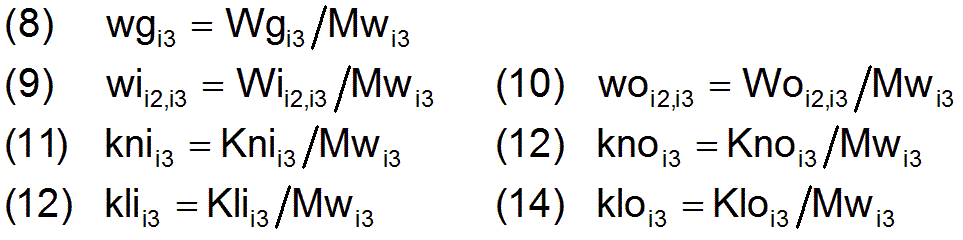
Zusammenfassend kann nun der komplette Parametersatz zur Darstellung der Produktivkräfte einer Volkswirtschaft in der hauptsächlich verwendeten dimensionslosen Form angegeben werden:
| a | Anzahl der Arbeitskräfte |
| ak | Anzahl der versorgten Arbeiter |
| fa | Vermehrungsfaktor der Arbeiter |
| kni | Input des notwendigen Konsums |
| kno | Output des notwendigen Konsums |
| kli | normierter Input des zusätzlichen Konsums |
| klo | normierter Output des zusätzlichen Konsums |
| fl | Faktor des zusätzlichen Konsums (Luxusfaktor) |
| ai | normierte Arbeitskräfte-Inputs |
| wi | normierte Produktionsmittelinputs |
| wo | normierte Produktionsoutputs |
| x | Produktionsvolumina |
| wg | Gesamtmengen der Wirtschaftsgüter |
Das ist der Mindestumfang an Parameter, der zur vollständigen Beschreibung des linearen diskreten Modells der Produktivkräfte einer Volkswirtschaft notwendig ist. Alle anderen Parameter lassen sich daraus ableiten.
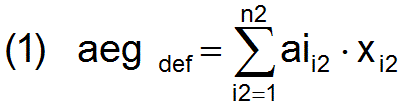
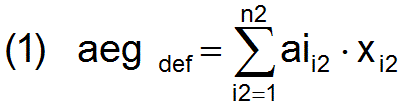
![]()
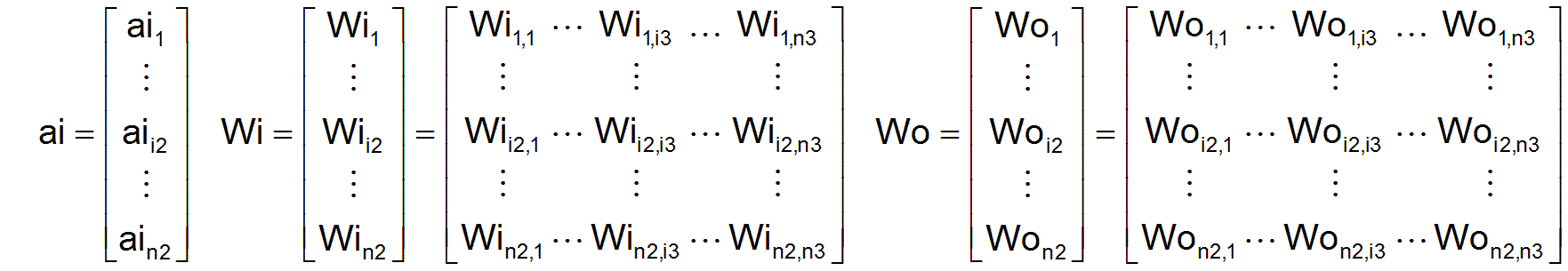
![]()
![]()
![]()
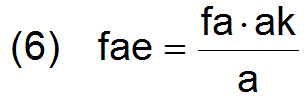
![]()