Mit dem oben bereits angegebenen Demonstrationsbeispiel wurde eine Testrechnung durch geführt. Neben den vorgegebenen zeitlich invarianten Parametern Produktivitätsmatrix p, Produktivitätsgruppengrößen ap und bedarfsgerechte Leistungsstruktur db0 bzw. dbn wurde die nicht optimale Beschäftigungsmatrix ac als Anfangsparameter angenommen. Dieser Datensatz muß noch durch einen Vektor ls von Stücklöhnen ergänzt werden, die als Anfangswerte dienen und nicht optimal sein müssen, da innerhalb der Simulationsrechnung ebenfalls eine Selbstoptimierung erfolgen soll. Als willkürlicher Anfangsvektor wurde festgelegt

Weiterhin müssen die empirischen Faktoren der Fluktuationsrate r1 und der Preisanpassungsgeschwindigkeit r2 angegeben werden. Es wurde angenommen

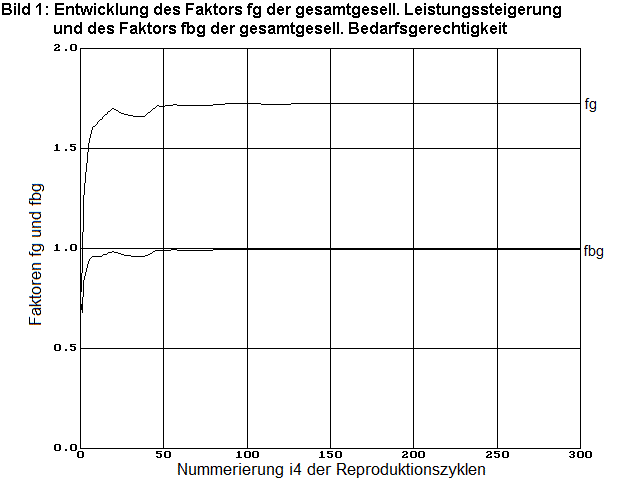
Es wurde über n4=300 Reproduktionszyklen gerechnet. Das Modell des Arbeitsmarktes konvergiert in unserem Beispiel tatsächlich zur optimalen Beschäftigungsmatrix ac_optimal, wie wir sie bereits auf anderem Wege errechnet haben. Nach ca. 100 Reproduktionszyklen ist die maximale Leistungssteigerung, darstellbar anhand des Faktors fg und einzeln anhand der Faktoren fp_j3, und die Bedarfsgerechtigkeit der Arbeitsleistungen, darstellbar anhand des Faktors fbg und einzeln anhand der Faktoren fb_j3, erreicht.

     fgn4=0     = 0,74      fpn4=0    =[1,00   1,00   1,00   1,00]

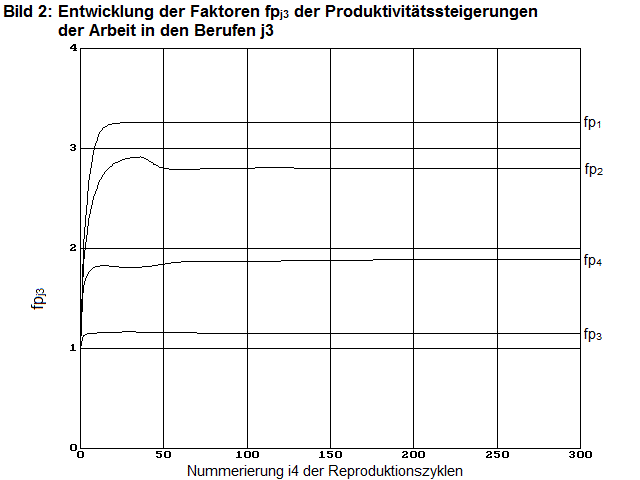
     fgn4=300  = 1,73      fpn4=300=[3,26   2,81    1,15   1,89]

und

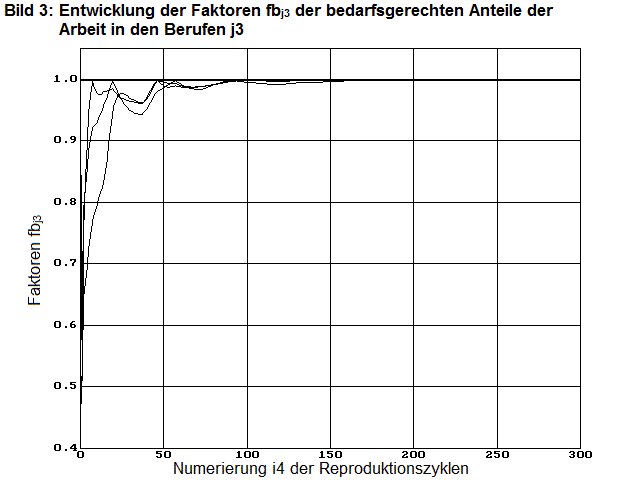
     fbgn4=0    = 0,74      fbn4=0   =[0,45   0,55   1,00   0,96]

     fbgn4=300= 1,00      fbn4=300=[1,00   1,00   1,00   1,00]

In den Bildern 1, 2, 3 zeigen Diagramme diese Faktoren in ihrem zeitlichen Verlauf von n4= 1 bis 300 und demonstrieren damit das Konvergenzverhalten des Modells an diesem Beispiel.

Auch die Stücklöhne ls_j3 konvergieren zu optimalen Werten. Hier sind die optimalen Werte allerdings erst nach ca. 150 Reproduktionszyklen erreicht, wie in Bild 4 zu erkennen ist.

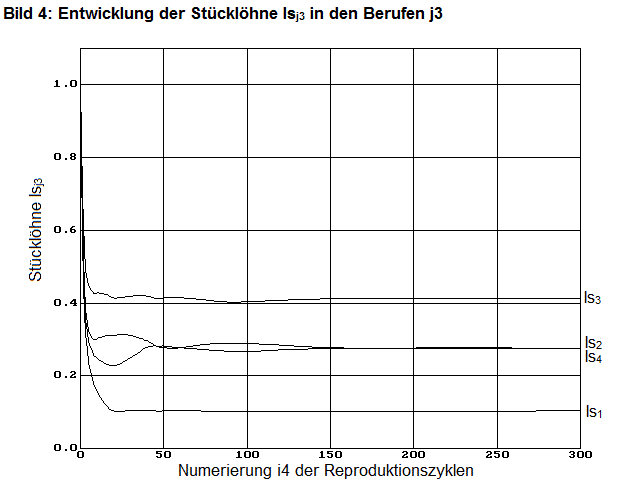
Nach 300 Reproduktionszyklen hatten die Stücklöhne ls_i4=300 folgende fast optimale Werte angenommen

Das Simulationsprogramm liefert auch die Matrix der individuellen Löhne l_i4=300 nach 300 Reproduktionszyklen. Im Zusammenhang mit der Beschäftigungsmatrix ac_i4=300 » ac_optimal ,die der optimalen Beschäftigungsmatrix entspricht, kann man daraus erkennen, welche Löhne die Arbeiter in ihren aktuellen Tätigkeiten tatsächlich realisieren und auch, welche sie z.Z. in den anderen Berufen realisieren könnten. In der nachfolgend angegebenen Matrix l_i4=300 sind die realisierten Löhne durch Fettdruck hervorgehoben. Als Ergänzung ist hier auch die zugehörige Beschäftigungsmatrix angegeben.

Das bemerkenswerte Ergebnis zeigt, das es tatsächlich ein optimales System von Stücklöhnen gibt, das bewirkt, daß ausnahmslos alle Arbeiter in der Tätigkeit, in der sie im Interesse einer gesamtgesellschaftlich maximalen bedarfsgerechten Arbeitsleistung tätig sind, auch tatsächlich individuell den höchsten Lohn erhalten. Demzufolge müßten sie bei ausreichender Information von sich aus bestrebt sein, genau in dem Beruf zu arbeiten. Außerdem ist an dem Ergebnis interessant, daß das System lediglich durch ein recht einfaches Prinzip der Lohnanpassung nach Angebot und Nachfrage selbstoptimierend zu optimalen Stücklöhnen und damit zu optimalen individuellen Löhnen geführt hat.