4 Demonstrationsbeispiel
An einem kleinen Demonstrationsbeispiel sollen nun die vorangegangenen Ausführungen illustriert werden. Es wird aber darauf hingewiesen, daß die angegebenen Werte in ihrer Auswahl und Größe willkürlich festgelegt wurden und eine annähernde Übereinstimmung mit tatsächlichen Verhältnissen nicht angestrebt wurde, weil sie bei einer derart geringen Anzahl von ausgewählten Berufen prinzipiell nicht möglich ist. Es geht um das Prinzip.
Es gibt 100 arbeitsfähige Mitglieder (Arbeiter) der Gesellschaft, d.h. a=100.
Es gibt 4 verschiedene Berufe, d.h. m3=4.
Die Arbeitsleistungen der Berufe sind in den entsprechenden Maßeinheiten meßbar:
| j3 | Beruf | Maßeinheit/Normal der Arbeitsleistung |
|---|---|---|
| 1 | Bauer | 100 kg Getreide pro Tag |
| 2 | Bäcker | 50 kg Brot pro Tag |
| 3 | Maurer | 1 m2 Gebäudenutzfläche pro Tag |
| 4 | Mechaniker | 0,1 Stück Maschine pro Tag |
Damit ist der Vektor der Maßeinheiten bzw. Normale der Arbeitsleistungen gegeben durch
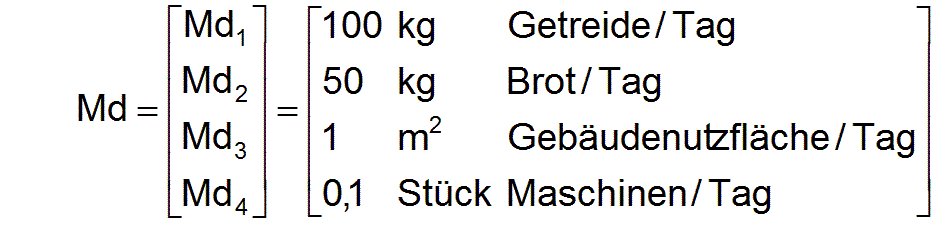
Mit diesen Normalen werden nachfolgend alle Parameter, die Arbeitsleistungen enthalten dimensionslos gemacht. Kurzbezeichnungen mit großem Anfangsbuchstaben stehen für dimensionsbehaftete Parameter und Kurzbezeichnungen mit kleinem Anfangsbuchstaben stehen für die entsprechenden dimensionslosen Parameter.
Es gibt 10 verschiedene Produktivitätsgruppen, d.h. m2=10 und zu jeder Produktivitätsgruppe gehören 10 Arbeiter, d.h. apj2 = 10 für alle j2= 1 bis m2. Die individuellen Produktivitätsprofile aller Arbeiter der Gesellschaft werden durch die dimensionslose Produktivitätsmatrix p beschrieben

Die erste Zeile der Produktivitätsmatrix p bedeutet z.B., daß ein Arbeiter der ersten Produktivitätsgruppe in der Lage ist, als Bauer (j3=1) 1 × 100 kg Getreide pro Tag zu produzieren, oder als Bäcker (j3=2) 1 × 50 kg Brot pro Tag zu Backen, oder als Maurer (j3=3) einen Teil eines Gebäudes, der im Durchschnitt 2 × 1 m2 Nutzfläche entspricht, zu errichten, oder als Mechaniker (j3=4) 4 × 0,1 Maschinen zu fertigen.
Es ist der Vektor db0 einer bedarfsgerechten Leistungsstruktur gegeben durch
db0 = [ 2 2 3 4 ]
Das bedeutet, daß die Arbeitsleistungen von 2 × 100 kg Getreide pro Tag und 2 × 50 kg Brot pro Tag und 3 × 1 m2 Gebäudenutzfläche pro Tag und 4 × 0,1 Maschinen pro Tag eine bedarfsgerecht Leitungsstruktur darstellen.
Jetzt soll noch eine Beschäftigungsmatrix vorgegeben werden, die noch nicht optimal sein soll, sondern willkürlich festgelegt ist. Als einfach überschaubares Beispiel sollen am Anfang in jedem Beruf jede Produktivitätsgruppe zu gleichen Anteilen enthalten sein und die Anzahl der Beschäftigten in jedem Beruf auch gleich sein. Damit ist am Anfang die Beschäftigungsmatrix ac vorgegeben durch.
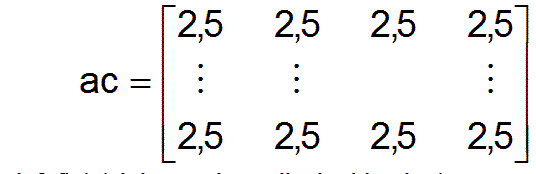
Damit sind alle primären Parameter gegeben.
Jetzt würde die Aufgabe bestehen eine optimale Beschäftigungsmatrix zu ermitteln, was aber erst nach Kenntnis der nächsten Abschnitte möglich ist. Zunächst können aber noch einige sekundäre Parameter dieses Demonstrationsbeispiels berechnet werden, die später für die Bewertung unserer Beschäftigungsmatrix geeignet sind.
Die normierten Produktivitäten pnj3 berechnen sich nach Gleichung (4) und ergeben folgende Werte:
pn = [ 2,45 2,00 1,65 2,30]
Die aktuellen mittleren Produktivitäten pmj3 berechnen sich nach der Gleichung (7) und ergeben mit der zur Zeit festgelegten Beschäftigungsmatrix folgende Werte:
pm = [ 2,45 2,00 1,65 2,30]
pn und pm sind z.Z. gleich, weil ja zunächst alle Produktivitätsgruppen in allen Berufen zu gleichen Teilen vertreten sind. Dadurch sind auch die Faktoren fpj3 der Produktivitätssteigerungen in den einzelnen Berufen alle gleich eins.
Mit fpj3= pmj3 / pnj3 sind fp1=1 fp2=1 fp3=1 fp4=1
D.h. mit der vorgegebenen Beschäftigungsmatrix ergibt sich noch keine Produktivitätssteigerung gegenüber den normierten Produktivitäten pn.
Die normierte bedarfsgerechte Leistungsstruktur berechnet sich nach der Gleichung (9) und ergibt folgende Werte:
dbn = [ 0,3722 0,3722 0,5583 0,7444 ]
Die Komponenten des Vektors d der gesamtgesellschaftlichen Arbeitsleistungen berechnen sich nach der Gleichung (5) und ergeben die Werte:
d = [ 61,25 50,00 41,25 57,50 ]
In dem Vektor d ist der maximale bedarfsgerechte Vektor db enthalten:
db = [ 27,50 27,50 41,25 55,00 ]
Der Vergleich des Vektors d mit dem Vektor db zeigt, daß nur die Leistungen im Beruf j3=3 übereinstimmen. Das heißt, daß z.Z. nur die Arbeiter im Beruf j3=4 alle für eine bedarfsgerechte Leistungsstruktur arbeiten, während in den anderen drei Berufen ein relatives Überangebot an Arbeitskräften besteht. Durch Fluktuation einiger Arbeiter aus den ersten drei Berufen in den 4.Beruf könnte z.B. der Vektor db vergrößert werden und das relative Überangebot an Arbeitskräften in den ersten drei Berufen reduziert werden.
Die Faktoren fbj3 zur Bewertung der Bedarfgerechtigkeit der Arbeitsleistungen in den einzelnen Berufen berechnen sich nach Gleichung (11)
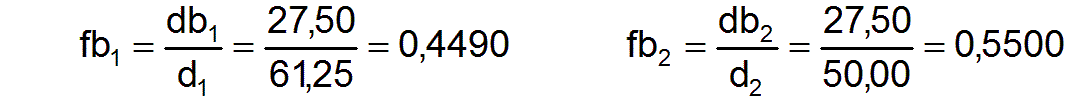
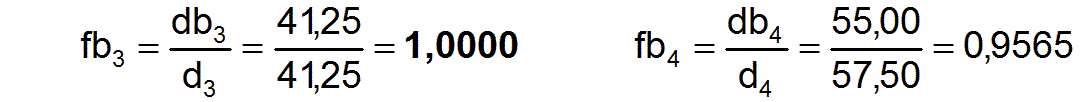
Sie zeigen, daß die Gesellschaft insgesamt noch weit von einer bedarfsgerechten Arbeitsleistung entfernt ist.
Der Faktor fbg der ein Maß für die gesamtgesellschaftliche Bedarfsgerechtigkeit der Arbeitsleistungen ist, berechnet sich nach der Gleichung (12) und ergibt den Wert
fbg =0,739
Der Faktor fg der gesamtgesellschaftlichen Leistungssteigerung berechnet sich nach einer der m3 Gleichungen (10).
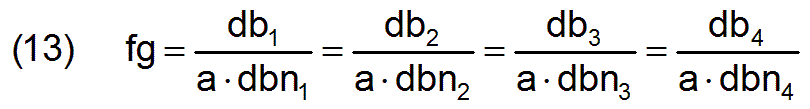
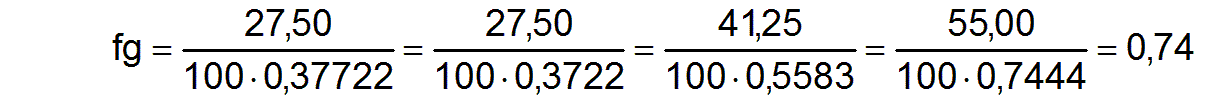
Dieser komplexe Faktor resultiert aus den jeweiligen Produktivitätssteigerungen in den einzelnen Berufen und aus den Bedarfsgerechtigkeiten der jeweiligen Berufe, die alle wiederum von der Beschäftigungsmatrix ac abhängen. Da die mittleren Produktivitäten pmj3 in unserem Beispiel alle gleich den normierten Produktivitäten pnj3 sind und damit alle fpj3=1 sind, ist fg=fbg. Dieses Beispiel zeigt bereits, daß durch unzweckmäßige Wahl der Beschäftigungsmatrix ac auch eine gesamtgesellschaftliche Leistungsverschlechterung eintreten kann. In unserem Fall wurde die Leistungsverschlechterung ausschließlich durch nicht bedarfsgerechte Arbeitsleistungen in den einzelnen Berufen bewirkt.
zurück weiter