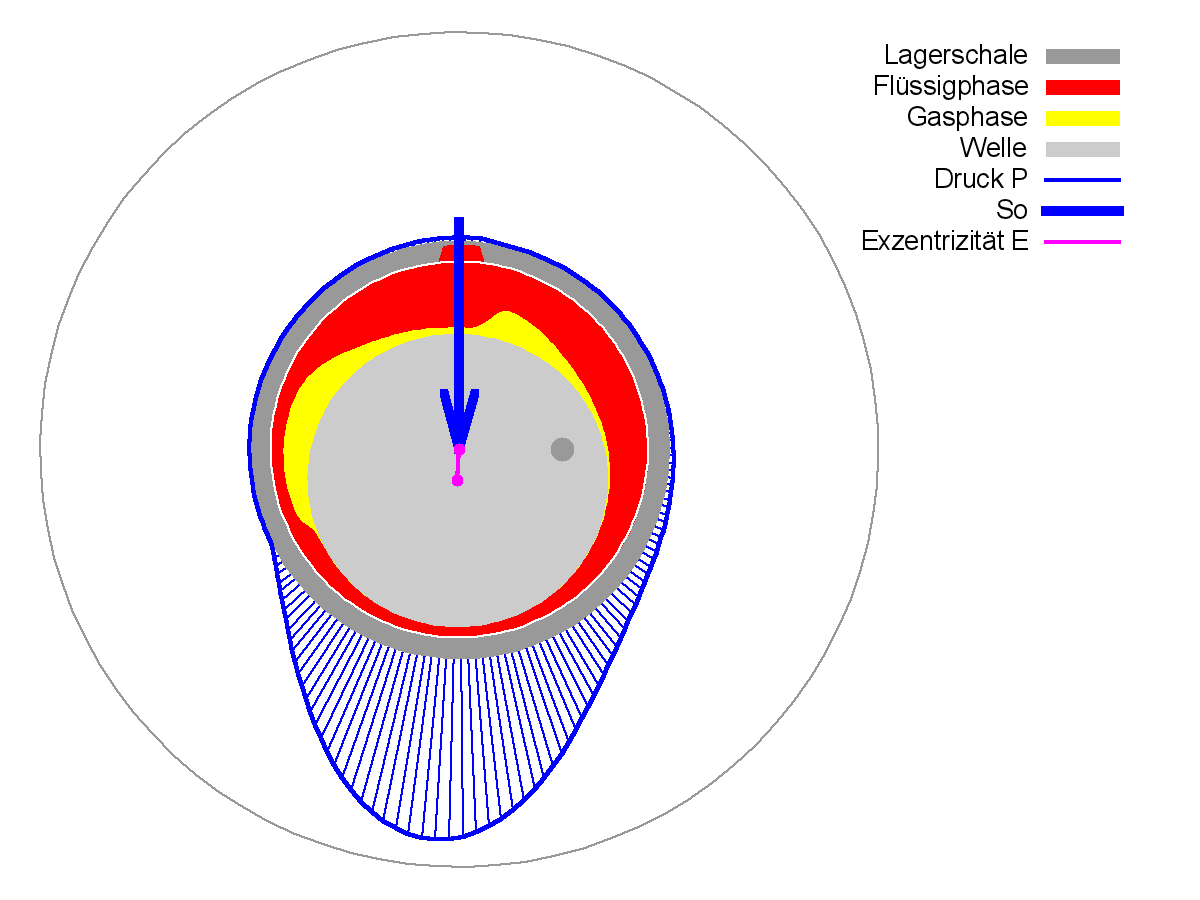
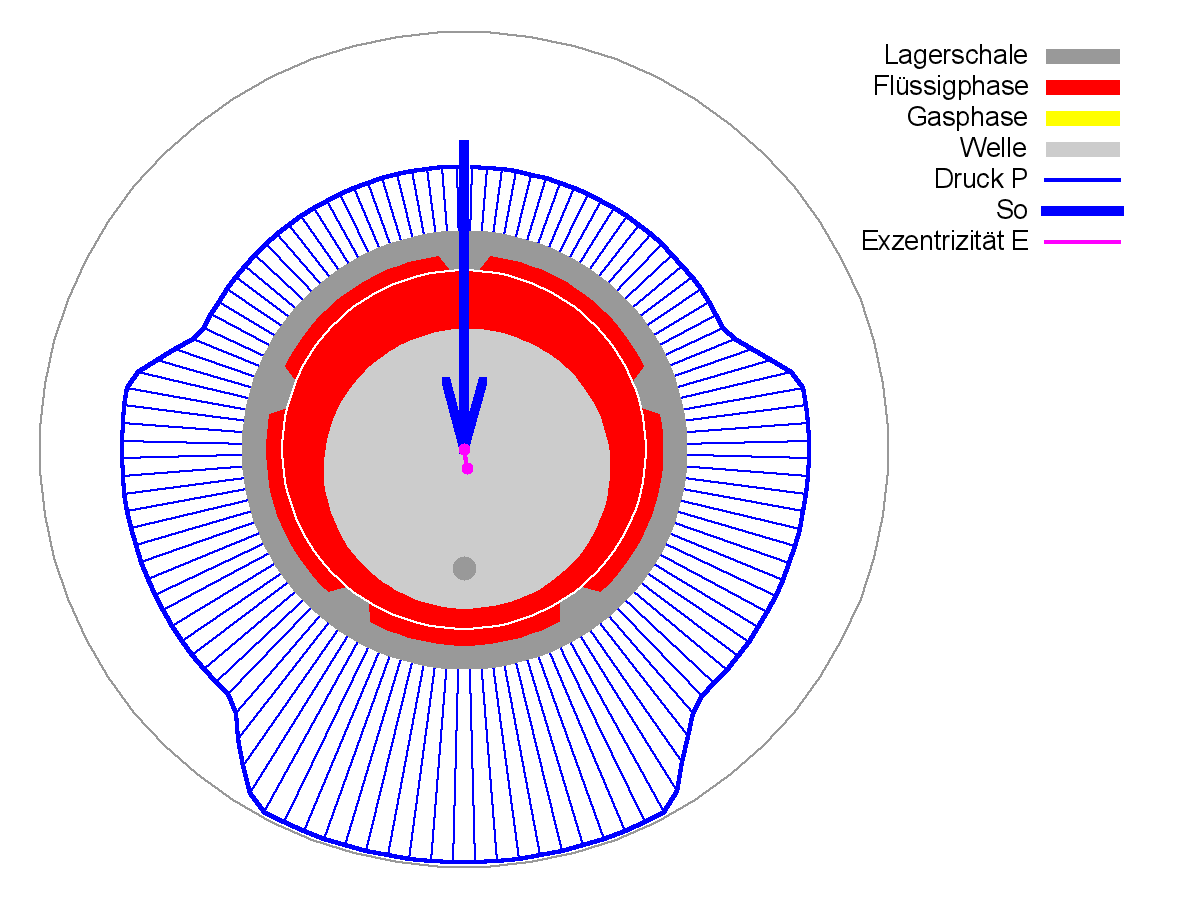
Bild 1: Druckverlauf und Schmiermittelverteilung in einem hydrodynamischen und einem hydrostatischen Radialgleitlager(Animationen links rechts)
1. Motivation
Die numerische Mathematik stellt eine reiche Auswahl zeitloser Lösungsalgorithmen und -strategien bereit, mit denen ingenieur-technische Probleme gelöst werden können. Dem Anwender fertig programmierter Simulationsverfahren bleiben diese meist verborgen unter der Benutzeroberfläche des jeweiligen Programms.
Durch Anpassen der Algorithmen an die spezielle Problematik kann die numerische Lösung des Problems oft beschleunigt werden. Manchmal wird die Lösung dadurch auch erst möglich. Ihre effektive Implementierung, insbesondere ihre Anpassung an die speziellen Bedingungen des jeweils zu lösenden Problems, erfordern eine vergleichbare Kreativität und Sachkenntnis, wie die Lösung des eigentlichen ingenieur-technischen Problems. Deshalb dürften Erkenntnisse über die Lösungsmethoden für die wissenschaftliche Öffentlichkeit von gleichem Interesse sein, wie die eigentlichen Ergebnisse zum untersuchten Problem.
Für das Gleitlagerberechnungsprogramm SIRIUS wurde eine umfangreiche Dokumentation erstellt, die weit über den Umfang einer Bedienanleitung hinausgeht, indem sie auch die mathematische Beschreibung des simulierten Objekts, die numerischen Lösungsverfahren und ihre rechentechnische Umsetzung ausführlich dokumentiert. Diese Dokumentation ist Grundlage der Veröffentlichung. An einigen Beispielen werden die Implementierung und Adaption von Lösungsalgorithmen dargestellt. Es werden einige prinzipielle Vorgehensweisen beschrieben.
zurück weiter2. Mathematische Beschreibung des technischen Objekts
Das abzubildende technische Objekt ist ein hydrodynamisch oder hydrostatisch geschmiertes Radialgleitlager.


Bild 1: Druckverlauf und Schmiermittelverteilung in einem hydrodynamischen und einem hydrostatischen Radialgleitlager(Animationen links rechts)
2.1. Die Reynolds'sche Gleichung, ein Spezialfall der Navier-Stokes-Gleichung für die Strömung im Schmierspal
Die Vorbereitung einer effektiven numerischen Lösung eines Problems beginnt bereits bei der mathematischen Formulierung, indem eine sinnvolle Abstraktion vorgenommen wird, so dass nur die wesentlichen Merkmale des physikalischen Prozesses abgebildet werden und unwesentliche Erscheinungen später nicht mit einem erheblichen Rechenaufwand durch die Berechnung geschleppt werden müssen.
Die Strömung im Schmierspalt weist durch den engen Schmierspalt einige spezielle Gegebenheiten auf, die einige für die Berechnung wesentliche Vereinfachungen zulassen. Die Kräfte der Flüssigkeitsreibung übersteigen bei Weitem die Beschleunigungskräfte in der Schmierflüssigkeit. Deshalb kann eine trägheitsfreie Strömung angenommen werden (kriechende Strömung). Außerdem können Strömungsgeschwindigkeiten senkrecht zu den Gleitflächen vernachlässigt werden. Das führt zur Reynolds'schen Differentialgleichung für die Strömung im Schmierspalt, wie sie bereits von Reynolds [2] und Sommerfeld [3] um 1900 hergeleitet wurde.
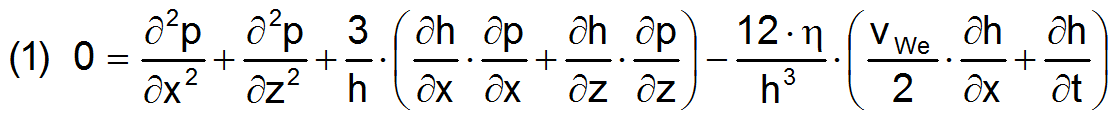
Die Reynolds'sche Gleichung der hydrodynamischen Schmierung ist ein Sonderfall der Navier-Stokes-Gleichung. Bereits über die Spalthöhe integriert reduziert sie die Strömung im 3-dimensionalen Schmierspalt auf ein zweidimensionales Problem. Sie ist eine partielle lineare Differentialgleichung zweiter Ordnung. Räumlich ist sie ein Randwertproblem und über die Zeit ein Anfangswertproblem. Das Differenzenverfahren ist dafür ein bewährtes Lösungsverfahren.
Bei dieser klassischen Reynolds'schen Gleichung gibt es aber noch ein Problem: Es wird nur die Strömung im Druckberg richtig beschrieben. Das Kavitationsgebiet im Lager wird hier aus der Berechnung ausgeschlossen. Dadurch ist eine korrekte Berechnung der erforderlichen Ölmengen und der Energiebilanz im Lager sowie des Einflusses der Anordnung der Schmiertaschen nur eingeschränkt möglich.
zurück weiter2.2 Die um Kavitation erweiterte Reynolds'sche Gleichung
In einer Erweiterung der Reynolds'schen Gleichung [4] wird die Schmierflüssigkeit als ein Zwei-Phasen-Kontinuum dargestellt, bestehend aus einer inkompressiblen, zähen, flüssigen Phase und einer kompressiblen, reibungslosen, gasförmigen Phase. Damit kann die Strömung im gesamten Schmierspalt abgebildet werden und so das Problem der Randbedingungen gelöst werden.
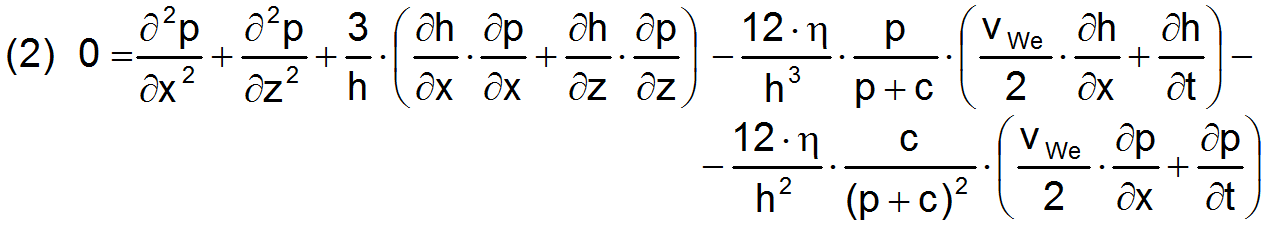
Sie ist ebenfalls eine partielle, aber nicht lineare Differentialgleichung zweiter Ordnung. Räumlich ist sie ebenfalls ein Randwertproblem und über die Zeit ein Anfangswertproblem. Als Randbedingungen brauchen hier nur noch die Bedingungen am Schmierspaltrand und an den Rändern von Schmiertaschen angegeben werden, die leicht zu formulieren sind. Die Randbedingungen für den Anfang und das Ende des Druckberges entfallen.
Als nicht lineare Differentialgleichung ist sie mit dem Differenzenverfahren nicht mehr direkt lösbar. Außerdem weist die Funktion des Druckes p(x,z,t) eine Schranke auf, nämlich die Bedingung p>0. Das ist der Anwendung des Differenzenverfahrens eher hinderlich. Mit entsprechenden Vorkehrungen ist seine Anwendung trotzdem möglich, wie nachfolgend gezeigt werden soll.
zurück weiter3. Numerische Lösungsverfahren
zurück weiter3.1. Die Linearisierung der erweiterten Reynolds'schen Differentialgleichung
Voraussetzung zur Lösung einer nicht linearen Differentialgleichung mit dem Differenzenverfahren ist ihre Linearisierung. Eine nicht lineare Funktion f(y) kann durch eine linearisierte Näherung in folgender Weise ersetzt werden.
3.2. Das Differenzenverfahren, ein universelles Lösungsverfahren für lineare Probleme und seine Adaption an ein nicht lineares Problem![]()
y0 ist dabei eine Anfangsnäherung der gesuchten Lösung y. Die erweiterte Reynolds'sche Differentialgleichung (2) enthält folgende nicht linearen Glieder.
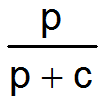 und
und 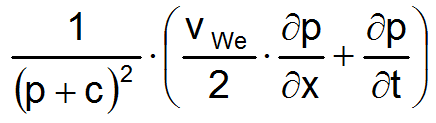
Das erste der beiden Glieder wird gemäß Gleichung (3) in folgender Weise linearisiert.
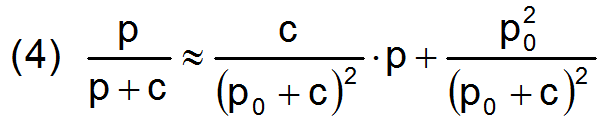
Auf die Angabe der weiteren Formeln wird hier verzichtet, da diese recht umfangreich und unübersichtlich werden und den Umfang des Artikels sprengen würden. Sie sind vollständig in dimensionsloser Form angegeben in [1, Abs. 3.4.1.3] oder [4, Abs. 7.3]. Damit erhält die erweiterte Reynolds'sche Differentialgleichung die lineare Form.
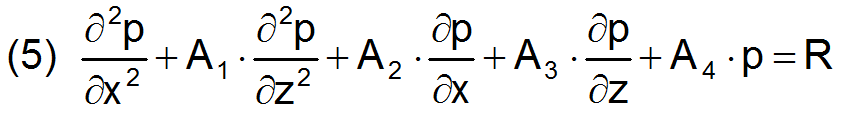
zurück weiter
Das Differenzenverfahren ist kein Lösungsalgorithmus im engeren Sinne, sondern eher ein Lösungsprinzip. Es beruht darauf, dass ein Kontinuum durch Punkte auf einem Gitternetz diskretisiert wird. Nur für diese Gitterpunkte wird eine Näherungslösung der Differentialgleichung berechnet.
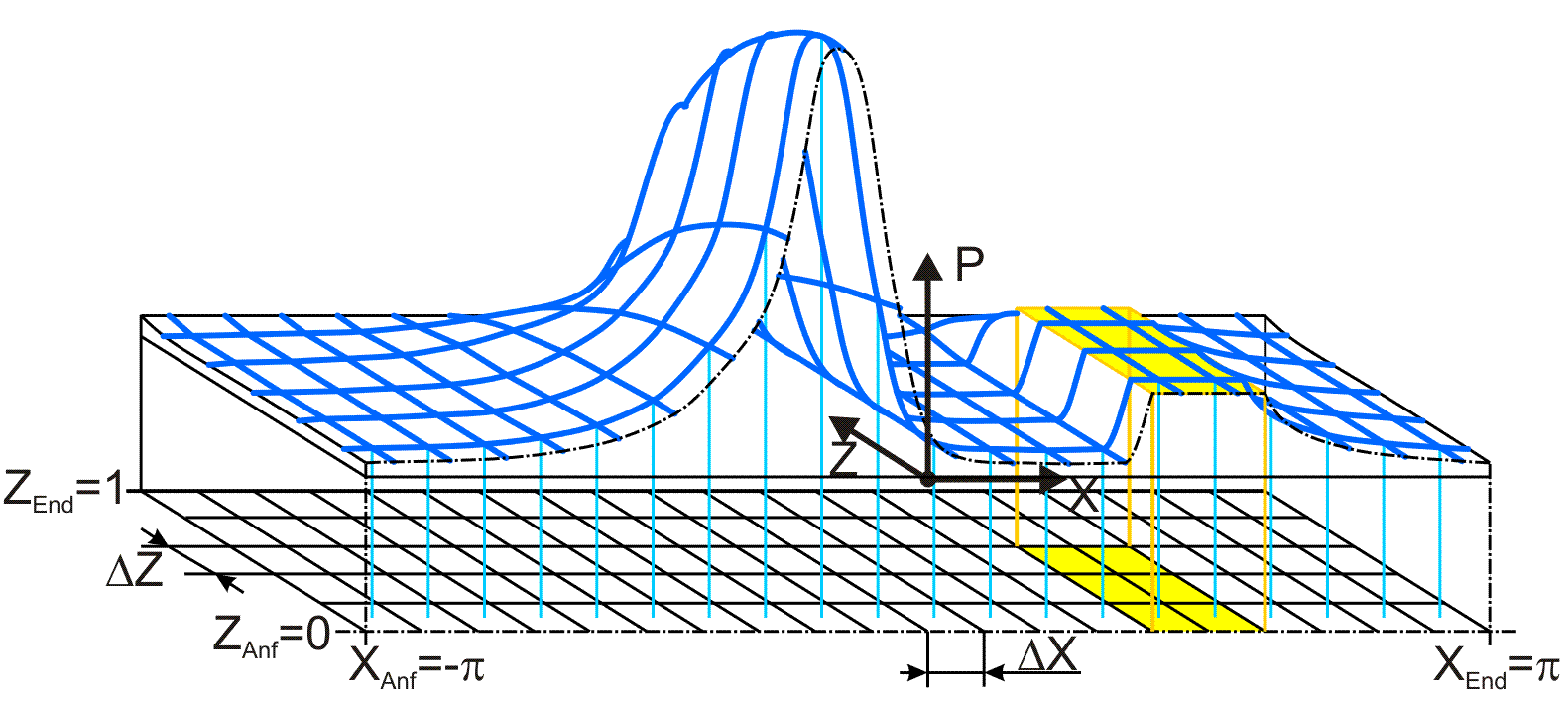
Bild 2: Diskretisierung der Schmierspaltfläche in NX·NZ Flächenelemente
Um diese Aufgabe zu lösen werden die partiellen Ableitungen (Differentialquotienten) durch Differenzenquotienten ersetzt [7]. Daher der Name Differenzenverfahren. Die 1. und 2. Ableitung der Funktion p(x) an der Stelle x wird z.B. bei äquidistanter Schrittweite des Gitternetzes gemäß Bild 3 durch die Differenzenformeln (6) und (7) ersetzt.
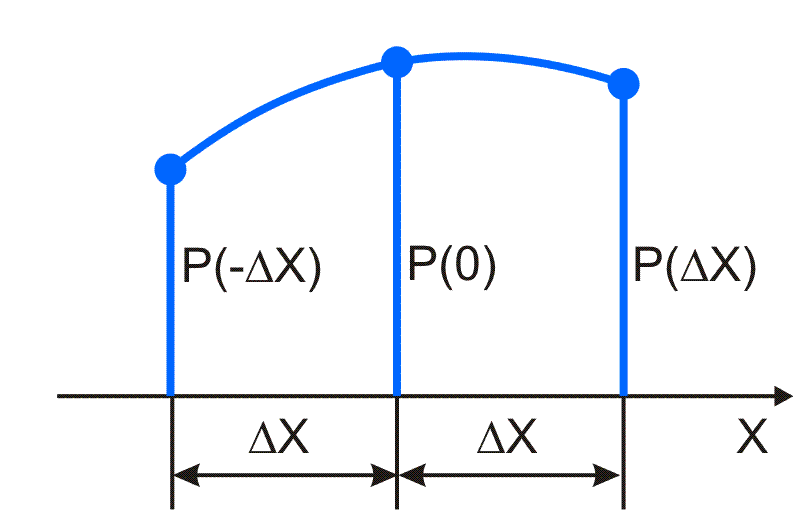
Bild 3: Approximation des Teilstücks der Funktion P(X)
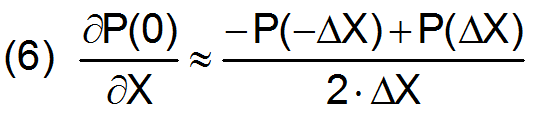
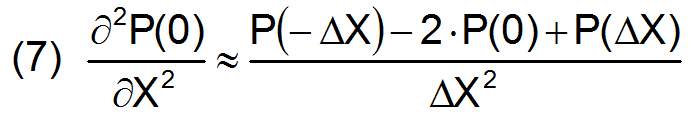
3.3. Aufstellen des Gleichungssystems
Nun kann für jeden Punkt des Gitternetzes eine Gleichung aufgestellt werden und es entsteht ein lineares Gleichungssystem zur Berechnung der Druckverteilung über die Schmierspaltfläche. Für die klassische Reynolds'sche Differentialgleichung liefert das einmalige Lösen des Gleichungssystems die endgültige Lösung. Für die erweiterte Reynolds-Gleichung muss zur iterativen Berechnung die Lösung des Gleichungssystems mehrfach durchlaufen werden. Die Erfahrung hat gezeigt, dass dazu in der Regel zwei Iterationszyklen reichen.
Bild 4 zeigt für ein sehr grobes Gitternetz mit nur 23 Stützstellen im Schmierspalt die Koeffizientenmatrix und in der rechten Spalte die rechten Seiten eines solchen Gleichungssystems. Nach den ersten 23 Gleichungen für die Berechnung des Schmierfilmdruckes, die das Differenzenverfahren repräsentieren, sind noch weitere Gleichungen hinzugefügt. Diese resultieren aus der mathematischen Abbildung eines peripheren Schmiersystems, das insbesondere für hydrostatische Lager erforderlich ist.
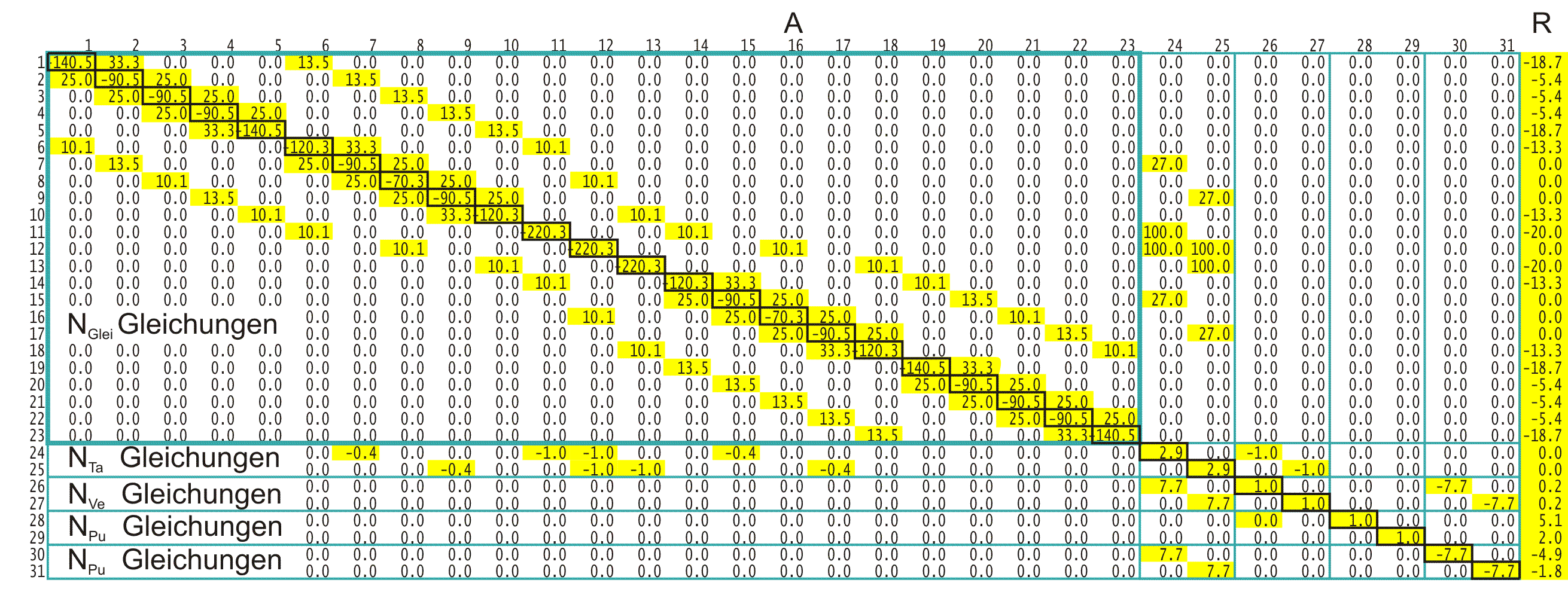
Bild 4: Koeffizientenmatrix und rechte Seiten eines Gleichungssystems [1, Abs.3.4.4]
Bild 5 skizziert z.B. ein peripheres Schmiersystem, welches alle Elemente enthält, die mit dem Programm SIRIUS abgebildet werden können. Für jede Schmiertasche im Lager ist eine weitere Gleichung erforderlich, die die Volumenbilanz der Schmiertasche abbildet. Für jede Verbindungsleitung ist eine weitere Gleichung erforderlich, die den Zusammenhang zwischen dem Druckgefälle in der Leitung und dem Volumenstrom durch die Leitung abbildet. Falls die entsprechende Gleichung, z.B. bei einer Spaltdrossel nicht linear ist, ist diese ebenfalls zu linearisieren und wird parallel zur iterativen Schmierfilmdruckberechnung gelöst. Für jede Schmiermittelpumpe sind noch zwei weitere Gleichungen erforderlich.

Bild 5: Prinzipskizze einer möglichen Variante des peripheren Universal-Schmiersystems
3.4. Das Gauß'sche Eliminationsverfahren ein Klassiker der numerischen Mathematik
Das Gauß'sche Eliminationsverfahren oder auch Gauß-Verfahren genannt ist ein klassisches Beispiel der zeitlosen Algorithmen. Es hat eine Schlüsselposition in der Lösung von linearen Gleichungssystemen, denn es stellt keine weiteren Anforderungen an das zu lösende Gleichungssystem, als die Forderung einer regulären Koeffizientenmatrix. Damit ist gewährleistet, dass es nur eine eindeutige Lösung gibt. Es stammt aus einer Zeit, als an elektronische Rechentechnik noch nicht zu denken war. Mit kleinen Verbesserungen, nämlich der Einführung der Pivotisierung, hat es in der modernen Rechentechnik weiterhin eine zentrale Bedeutung.
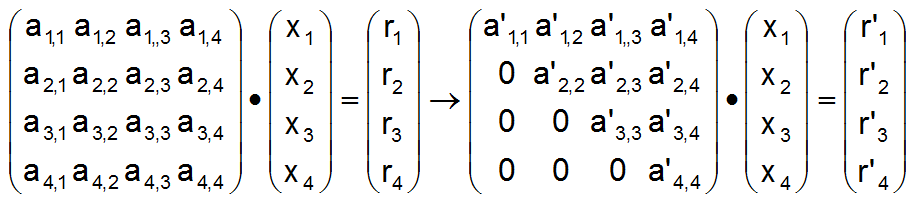
Es ist ein direkter Gleichungslöser. Das Lösungsprinzip beruht auf der Umwandlung der quadratischen Koeffizientenmatrix A des ursprünglichen Gleichungssystems in eine Dreiecksmatrix A', ohne dass sich der Lösungsvektor X verändert. Das modifizierte Gleichungssystem kann dann einfach rekursiv gelöst werden, beginnend mit der letzten Gleichung. Bild 6 skizziert ein ursprüngliches und ein modifiziertes Gleichungssystem in Matrizenschreibweise.
3.5. Vom Gauß-Algorithmus zum modernen GMRES-Verfahren
In älteren Versionen des Programms SIRIUS wurde das Gauß-Verfahren erfolgreich eingesetzt. Dieses Verfahren hat aber die Eigenschaft, dass sich bei jeder Verdopplung der Anzahl der Unbekannten die Anzahl der erforderlichen Lösungsoperationen mit dem Faktor 23=8 erhöht. Damit wird bei größeren Gitternetzen das Warten auf ein Ergebnis recht langweilig, weil dieser exponentielle Anstieg der Rechenzeit auf Dauer auch nicht durch schnellere Computer aufgefangen werden kann.
Mit der flächendeckenden Verbreitung der Rechentechnik wurde verstärkt in den 1960-iger und 1970-iger Jahren nach schnelleren Lösungsverfahren gesucht, so dass heute eine Palette von wesentlich schnelleren Gleichungslösern zur Verfügung steht. Bei der Lösung ingenieur-technischer Probleme sind die Koeffizientenmatrizen oft nur dünn besetzt, d.h. die meisten Koeffizienten sind Null, wie bereits die Matrix im Bild 4 zeigt. Das machen sich eine Reihe von Verfahren zu nutze. Es werden aber auch andere Merkmale zur Reduktion der Anzahl erforderlicher Lösungsoperationen ausgenutzt. Es ist deshalb erforderlich zur Aufgabe das passende Lösungsverfahren auszuwählen. Die meisten dieser Verfahren sind Iterationsverfahren, die mehrfach durchlaufen werden müssen, aber bei großen Koeffizientenmatrizen trotzdem wesentlich schneller rechnen. Einen guten Überblick über die gängigen Verfahren gibt Meister [6] oder die Internet-Plattform "Wikipedia".
Für das Gleichungssystems zur Lösung der Reynolds'schen Gleichung mit dem Differenzenverfahren einschließlich der Gleichungen des peripheren Schmiersystems erschien das GMRES-Verfahren (Generalized minimal residual method) geeignet und wurde in das Programm SIRIUS implementiert. Es wird als Näherungsverfahren verwendet und arbeitet erst richtig schnell in Kombination mit einem Vorkonditionierer. Als Vorkonditionierung wird die ILU-Zerlegung (incomplete Lower-Upper-Decomposition) verwendet. Bei einer Anzahl von ca. 10 000 Unbekannten wurde damit gegenüber dem Gauß-Verfahren eine Beschleunigung um den Faktor 1000 erreicht. Ein wesentlicher Vorteil dieses Verfahrens besteht darin, dass die Rechenzeit nur etwa proportional mit der Anzahl der Unbekannten steigt.
Ein weiterer Vorteil ist, dass das Verfahren mit einer "gepackten Matrix" arbeitet, in der nur die Nicht-Null-Koeffizienten abgespeichert sind. Wenn man das Programm so schreibt, dass die "gepackte Matrix" direkt erzeugt wird, was allerdings ziemlich anspruchsvolle Programmierung ist, wird erheblich Speicherplatz gespart. Bild 7 zeigt die Koeffizientenmatrix aus Bild 4 in gepackter Form.
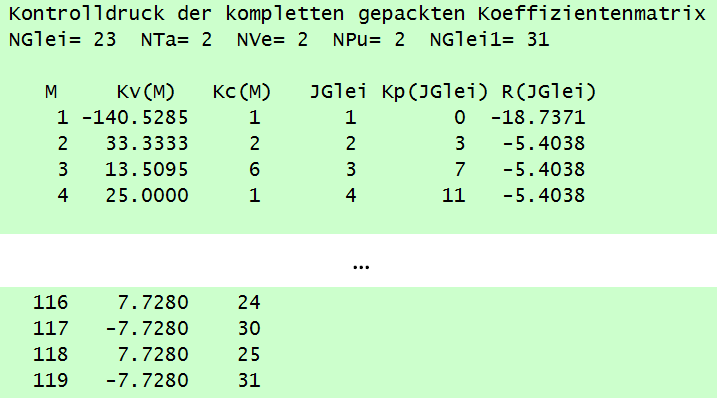
Die Koeffizientenmatrix wird hier ersetzt durch 4 Vektoren, die nur die Werte der Nicht-Null-Koeffizienten und ihre Stellung in der ursprünglichen Matrix angeben. [1, Abs. 3.4.4]
zurück weiter3.6. Die Berechnung der Wellenverlagerung durch ein 2·2-dimensionales Newton'sches Näherungsverfahren und seine Lösung mit einem geometrischen Lösungsansatz
Mit Hilfe der Reynolds'schen Differentialgleichung kann aus einer vorgegebenen Spaltgeometrie der Druckverlauf im Schmierspalt berechnet werden und durch Integration der Schmierspaltdrücke der resultierende Vektor der Lagerbelastung [F1,F2]. In der Praxis ist die Problemstellung aber umgekehrt. Infolge des Vektors der Lagerbelastung [F1,F2] verlagert sich die Welle innerhalb des Lagerspielraums, bis der dadurch entstehende Schmierfilmdruck mit der Lagerbelastung im Gleichgewicht steht. Es ist also der Vektor der Wellenverlagerung [E1,E2] zu ermitteln.
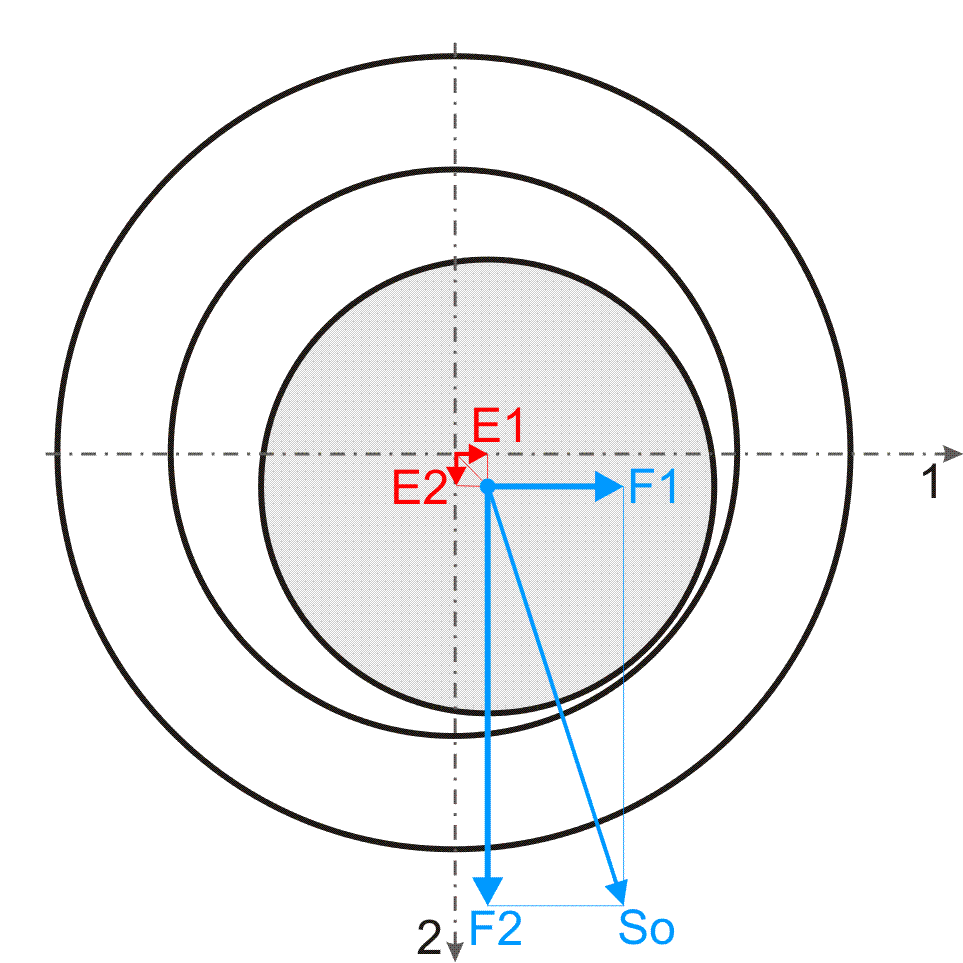
Bild 8: Komponenten der Lagerbelastung und der Exzentrizität im Lager
Formal kann man den Zusammenhang zwischen den Komponenten der Lagerbelastung F1 und F2 und der Spaltgeometrie E1 und E2 als die Funktionen func1 und func2 formulieren.
![]()
![]()
Damit ist ein nicht lineares Gleichungssystem mit 2 Gleichungen und den 2 Unbekannten E1 und E2 zu lösen. Jeder Punkt der 2 Funktionen bedeutet die komplette Berechnung einer Druckverteilung im Schmierspalt. In der Umgebung um eine vorhandene Näherungslösung kann man die beiden Funktionen durch zwei tangentiale Ebenen 1 und 2 approximieren (Bild 9, linke Skizze).
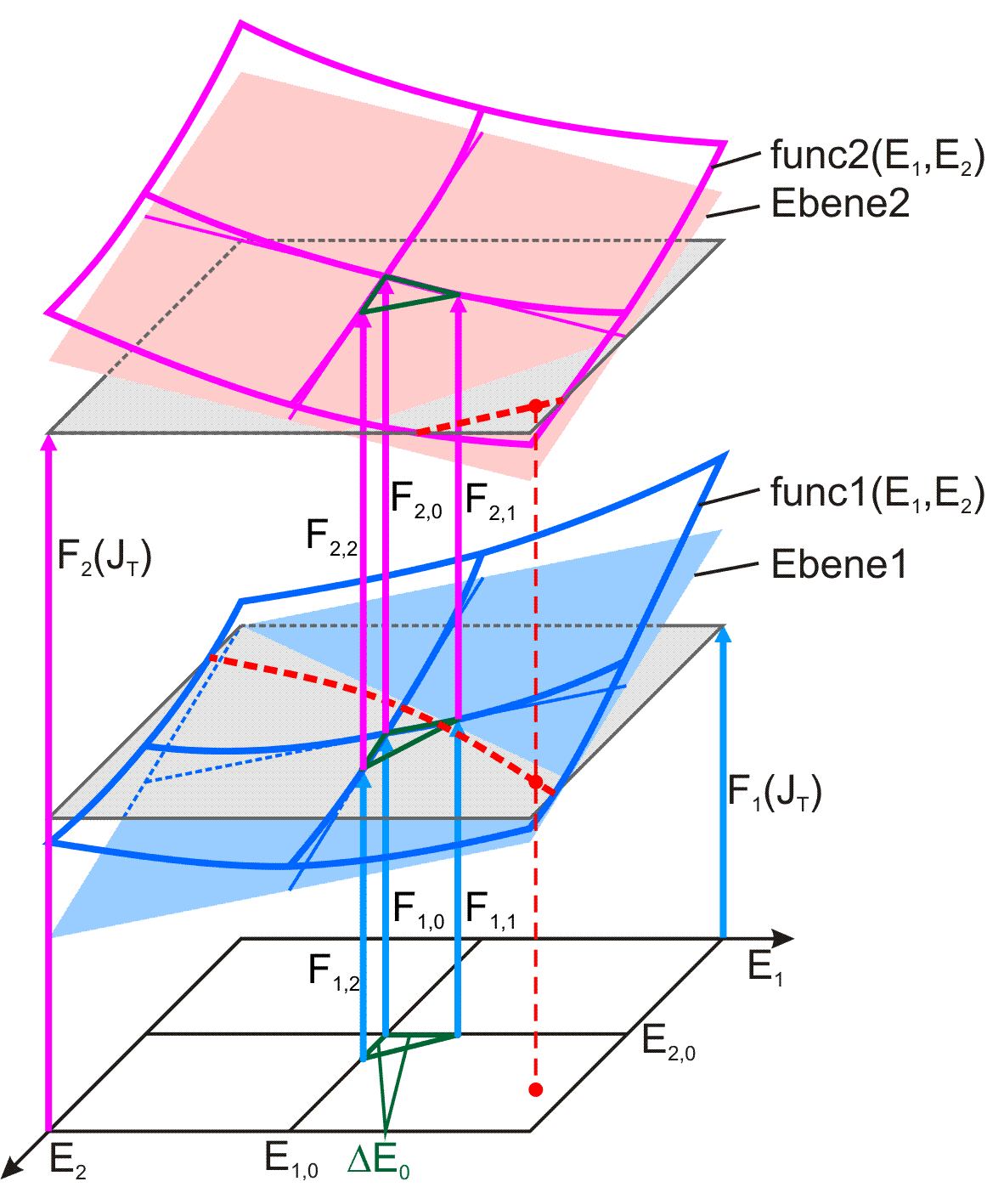

Bild 9: Grafische Darstellung der Ermittlung eines Wellenverlagerungspunktes [E1,E2]
Gemäß Bild 9, rechte Skizze lässt sich ein Iterationsschritt der Lösung des Gleichungssystems grafisch darstellen. Es ist der Schnittpunkt der Projektionen der Schnittlinien S1 und S2 auf die Koordinatenebenen E1-E2. Daraus lassen sich dann leicht die Berechnungsformeln herleiten. Sie sind vollständig angegeben in [5, Abs. 4.1.3] und [1, Abs. 3.4.7.3].
Wird diese Berechnung mehrfach wiederholt, indem der berechnete Schnittpunkt als Basispunkt der nächsten Iteration verwendet wird, konvergiert die Iteration zur Lösung des nicht linearen Gleichungssystems.
Dieses Verfahren stellt ein erweitertes Newton'sches Näherungsverfahren dar, wie es in Bild 10 vereinfacht als eindimensionales Problem skizziert ist [7]. Es ist ein Standardverfahren, welches lange Zeit vor der elektronischen Rechentechnik entwickelt wurde.
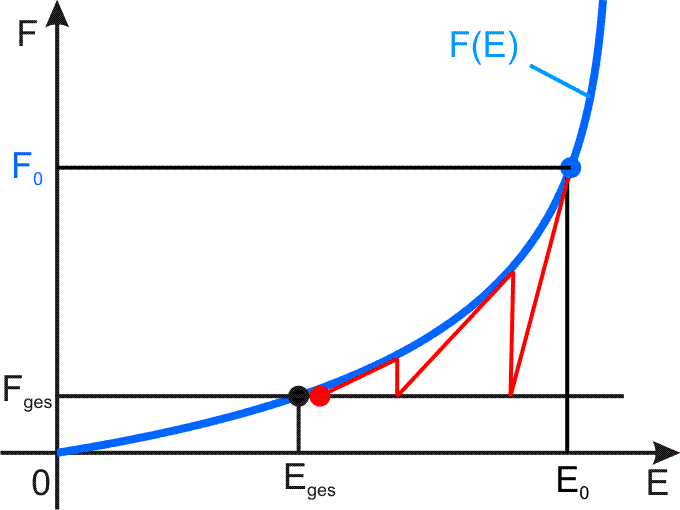
Bild 10: Newton'sches Näherungsverfahren
4. Schlussbemerkungen
Maschinenbau-Ingenieure sind nicht nur Nutzer von Berechnungsprogrammen, sondern notwendiger Weise beteiligt an ihrer Erzeugung. Sie müssen bzw. können:
1. die technischen Probleme mathematisch formulieren,
2. kompetente Gesprächspartner der Mathematiker und Informatiker sein,
3. aus ihrer Kenntnis des technischen Objekts zu kreativen Lösungsansätzen beitragen,
4. evtl. die numerischen Probleme eigenständig lösen und programmieren.
Deshalb ist es notwendig, dass auch sie grundlegende Kenntnisse über diese zeitlosen mathematischen Lösungsalgorithmen besitzen, zumal diese universell anwendbar sind. Im Rahmen des Vortrags konnten nur des prinzipielle Vorgehen beschrieben werden. Wesentlich ausführlicher und mit Angabe aller erforderlichen Formeln wird das in der Dokumentation zum Programm SIRIUS [1] dargestellt.
zurück zurück zum Anfang